基于ESMD方法的上川岛降水多尺度特征分析

余兴湛，黄国成，方英城，雷琳

（1.台山市气象局，广东台山 529200；2.广宁县气象局，广东广宁 526300）

上川岛地处南海之滨，属南亚热带海洋性季风型气候，在夏季常受西南季风的影响，是台风、暴雨、雷雨大风、干旱等气象灾害频发的地区［1－2］。目前尚未有专家学者对上川岛降水特征进行分析，因此对上川岛降水进行多尺度特征分析，能为当地的降水预报和防灾减灾救灾提供参考，对当地的旅游发展、农业生产和生命财产安全等有重要的意义。

降水时间序列特征不仅有趋势、突变等的非周期变化，也有不同时间尺度上的周期变化，是气象学者关注的热点，目前在这方面已有研究［3－4］。华南地区多个市县对当地的降水特征也做了不少的的研究［5－9］。但是气候系统是非常复杂的，它不但具有非线性和非平稳性，而且有层次性，许多不同大小的时空尺度构成了多层次结构［10］。近些年在Hilbert－Huang变换基础上发展出的极点对称模态分解（ESMD）方法，在数据分析上具有极高灵活性和自适应性，非常适合非线性非平稳数据的多尺度分析，目前已被应用于电气工程、信息科学、大气科学和机械工程等领域数据的分析研究上［11－14］。鉴于此，本研究采用ESMD方法对1958—2020年上川岛的年降水序列进行多时间尺度分析，并用小波分析、M－K检验法对ESMD方法的结果进行对比验证，试图为今后上川岛降水预报和防灾减灾救灾提供参考。

1 研究数据和方法

利用上川岛国家气象观测站1958—2020年的逐年降水资料，运用ESMD方法、小波分析、M－K检验法等方法进行分析。ESMD方法借鉴了经验模态分解（EMD）思想，将外部包络线插值改为内部极点对称插值，借用“最小二乘”的想法来优化最后剩余模态使其成为整个数据的“自适应全局均线”，并由此来确定最佳筛选次数，ESMD具体计算方法和步骤见参考文献［14］。

2 上川岛降水年际变化

上川岛多年平均降水量为2 227.8mm，年最大降水量为3 657.7 mm，出现在1973年；年最小降水量为1 028.1 mm，出现在1977年。对上川岛年降水量序列进行线性拟合（图1a），可以看出，上川岛年降水序列总体上呈现出上升的趋势，每年降水量增加5.23 mm。为了进一步分析其变化趋势的显著性和突变情况，采用M－K检验法计算出M－K趋势系数并作M－K检验曲线（图1b）。通过计算得出M－K趋势系数为0.979 8，这表明年降水量呈上升趋势，但并未通过置信度90%的显著性检验。由M－K检验曲线图可以发现UF和UB两条曲线出现了非常多的交点，说明上川岛年降水序列没有出现明显的突变。

图1 1958—2020年上川岛年降雨量变化（a）和M－K检验曲线（b）

3 降水变化的多尺度分析

运用ESMD方法对1958—2020年上川岛降水序列进行分解，其最佳筛选次数为24，此时得到4个模态分量（模态1—4）和1个剩余模态R，如图2所示。

图2 上川岛降水序列ESMD分解的模态分量及剩余模态R

分解出来的每个模态都有其独立的物理意义，其中剩余模态是原始数据的最佳自适应全局均线，而模态1—4可以看成不同时间尺度的振动子信号，各自代表了原降水序列不同时间尺度的振荡特征。运用快速傅里叶变换（FFT）周期图法求出每个模态分量的平均周期，再计算出各自对原降水序列的方差贡献率（表1）。

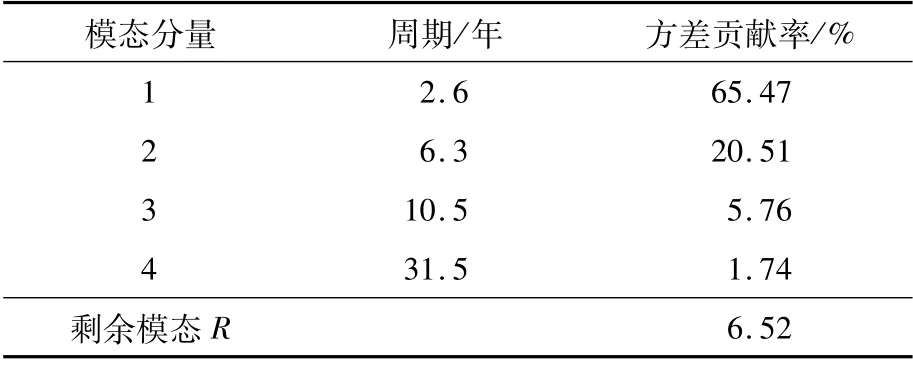
表1 降水序列各模态分量的方差贡献率

结合图2和表1可以发现，模态1表现出2.6年的周期振荡，其方差贡献率高达65.47%，表明上川岛年降水量序列以2.6年为周期的振荡最为显著，这种周期振荡主要表现在1968—1982、1985—1996、2004—2012年这3个阶段，说明这3个阶段的降水变化幅度比较明显。模态2表现出6.3年的周期振荡，其方差贡献率为20.51%，表明年降水序列以6.3年为周期振荡的信号十分明显，其振幅表现为增多－减少－增多的循环变化。模态3和模态4分别表现出10.5和31.5年的周期振荡，它们的方差贡献率为5.76%和1.74%，表明年降水序列在周期为10.5和31.5年的振荡比较稳定。最佳自适应全局均线的方差贡献率为6.52%，从图3可以看到，其在随时间变化序列上与上川岛年降水量有很好的对应关系，这表明ESMD方法的分解是可靠的。此外，还可以看到在1958—1973年降水量呈上升趋势，1974—1993年降水量呈小幅下降趋势，1994—2020年降水量又呈上升趋势，整体呈上升趋势。因此，上川岛年降水量序列的变化是非线性增加，并不是简单的线性持续增加。

图3 最佳自适应全局均线与实况雨量拟合图

为了验证ESMD方法分析出的周期振荡特征的合理性，本研究利用小波分析进行对比验证。小波分析能同时反映出信号的时域和频域特征，在气候分析中应用非常广泛［15］。图4为上川岛年降水量序列的小波系数实部图和方差图。从图4中可以看到，上川岛年降水量序列存在3～4、准9、准12、准33年的周期振荡。对比小波分析和ESMD方法的周期结果，发现两者的结果比较相近，但有一定的差异。这可能是因为上川岛年降水量序列是非线性非平稳数据，小波分析理论基础是线性叠加原理，在处理非线性数据上有一定的局限性，而ESMD方法是在Hilbert－Huang变换基础上的新发展，是一种具有极高灵活性和自适应性的数据分析方法，十分适合非线性非平稳数据的多尺度分析。

图4 1958—2020年上川站年降水序列Morlet小波变换系数实部（a）和小波方差（b）

4 不同时间尺度下的降水突变分析

为了研究不同时间尺度下的上川岛年降水量序列的突变情况，应用直接插值法求出4个模态的瞬时频率和瞬时振幅，并绘制出其与时间的变化图，见图5。

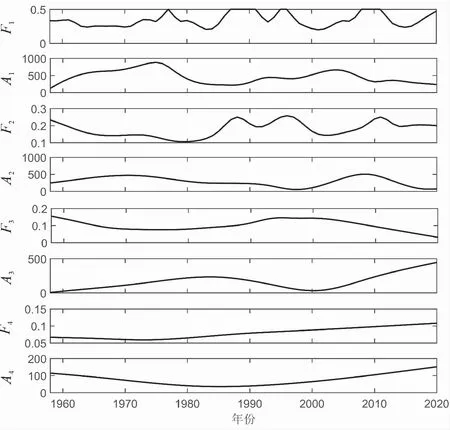
图5 各模态频率（F）与振幅（A）的时间变化

其中F1—F4为模态1—4的频率，A1—A4为模态1—4的振幅。由F1和A1可得，1986年出现了突然的高频、小振幅振荡，说明2.5年尺度的突变发生在1986年。由F2和A2可知，1995年出现了突然的高频、小振幅振荡，说明6.3年尺度的突变发生在1995年。由F3和A3发现，2000年出现了突然的高频、小振幅振荡，说明10.5年尺度的突变发生在2000年。由F4和A4得到，模态频率从1972年开始一直增高，而模态振幅从1985年开始一直变大，说明在31.5年尺度上的上川岛年降水量自1985年开始持续上升。

5 结论

1）上川岛年降水量变化以年际尺度上周期变化为主，有2.6和6.3年的周期振荡，方差贡献率分别为65.47%和20.51%；年代际尺度上以10.5和31.5年周期振荡为主。

2）2.6、6.3和10.5年尺度下的突变时间分别为1986、1995和2000年。31.5年尺度上没有明显的突变时间，该尺度的年降水量自1985年开始持续上升。

3）利用ESMD方法可以将不同时间尺度的序列有效分离，便于诊断多时间尺度的周期、趋势和突变特征。

ESMD方法在分析非线性、非平稳数据方面有其特殊的优势，其对于气象数据分解的可靠性、各个模态分量的权重判断以及如何将其应用到气候预测上等方面仍需要进一步的探讨和验证。