基于ANSYS的架空输电线脱冰跳跃动态特性研究

黄 强，连 雯，张翰涛，王 琼，胡淑兵

（1.中国电建集团江西省电力设计院有限公司，江西 南昌 330096；2.国网上海市电力公司浦东供电公司，上海 200120）

0 引言

输电线路脱冰跳跃是指冰区输电线路的覆冰在温度等自然条件下脱落引起导线的上、下振动，工程中称为“冰跳”。冰跳过程中各相导线之间及导地线之间的间隙可能小于相应的绝缘间隙，从而导致闪络、烧伤甚至烧断导线等电气事故[1-3]。

在现有的输电线路脱冰跳跃研究中，主要研究方法包括覆冰导线的实际观测、导线脱冰试验研究[4-6]、脱冰跳跃数值仿真研究[7-9]。其中由于实际观测受到气象条件的限制，持续时间长且成本较高，各单位公开的资料较少。而脱冰跳跃仿真研究相较于脱冰试验研究更容易实现，且成本较低。文中基于ANSYS对不同覆冰工况导线脱冰跳跃做有限元计算，并分析了导线脱冰跳跃的动态特性。

1 基本原理

1.1 架空线的基本特性

架空线属于典型的索结构，不能承受压力和弯矩，主要依靠索的抗拉性能来承受外部荷载[10]。针对架空线的基本特性做出如下假设：

1）忽略间隔棒的作用，将分裂导线等效为单根导线，并且不考虑导线的扭转刚度；

2）输电线采用索单元模型，考虑其几何非线性，满足虎克定律；

3）输电线路的舞动只在垂直方向发生，不考虑水平和扭转方向的舞动。

1.2 导线的初始构型

在现有的研究中，因架空输电线的长度远大于其截面尺寸，通常认为导线的几何形状受材料的刚性影响很小，可将其线视为一根柔软的链条，处处受铰接，只能承受轴向力而不能承受弯矩[10]。另外，通常认为导线上的载荷是延线长均匀分布的，如图1所示，由此得到悬链线方程，如式（1）。

图1 导线上的载荷分布情况（悬链线）

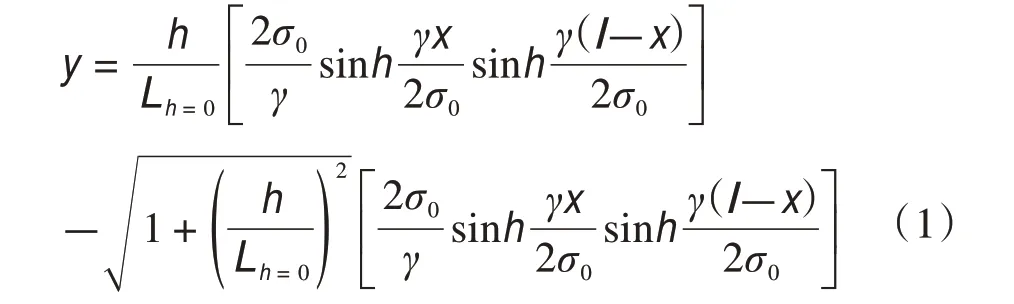
式中，h为悬挂点的高差，σ0为弧垂最低点的应力；γ为垂直比载；l为悬点的水平距离；Lh=0为悬点高度相同时架空线的线长，见式（2）。

不等高悬点架空线的线长见式（3）。

1.3 导线覆冰载荷模拟方法

导线覆冰载荷常用的模拟方法有：等效集中质量法、等效密度法、附加冰单元法，其建模思路如下：

1）等效集中质量法：线上的覆冰被转换成一系列均匀的集中质量，其作为外部负载施加到线上，并且每根导线的冰重量可通过式（4）计算。

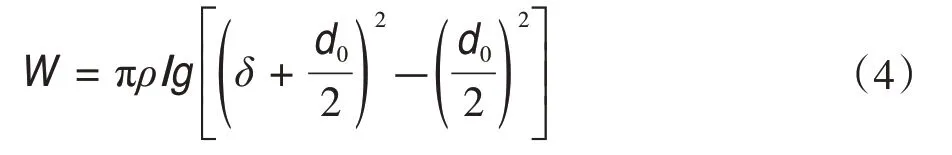
式中，ρ为覆冰密度，一般取0.9 g/cm3；δ为覆冰厚度；l为输电线的档距；g为重力加速度，一般取g=9.805 m/s2；d0为导线外径。

2）等效密度方法：通常认为输电线表面上的冰涂层沿着线均匀分布，因此冰负荷可以等于线密度的增加，其等效密度可按式（5）计算。

式中，W1、W2分别为输电导线的自重和覆冰重量，kg/m；A为导线的截面积，m2；ρ1为输电导线密度；ρ2为增加的密度值。

3）附加冰单元法：在输电导线脱冰跳跃仿真建模时，将导线上的覆冰作为与导线单元平行的“Pipe”单元，并与导线单元共用节点。

2 建模方法

针对架空输电线路的强非线性的特点，采用目前结构分析中使用最为广泛的通用程序之一ANSYS，其具有较好的建模和分析能力。文中根据架空线悬链线理论和方程，编写导线初始构型程序，得出架线后导线的初始构型；然后在ANSYS中建立架空输电线的非线性有限元模型，并分析覆冰架空输电线脱冰跳跃动态特性。

非线性有限元法的基本原理是在架空线弦线位置创建几何模型，采用适当的初应变和较小的弹性模量，施加自重荷载，逐步更新有限元模型；设定收敛条件，当结果满足收敛条件时退出循环迭代求解，其流程如图2所示。

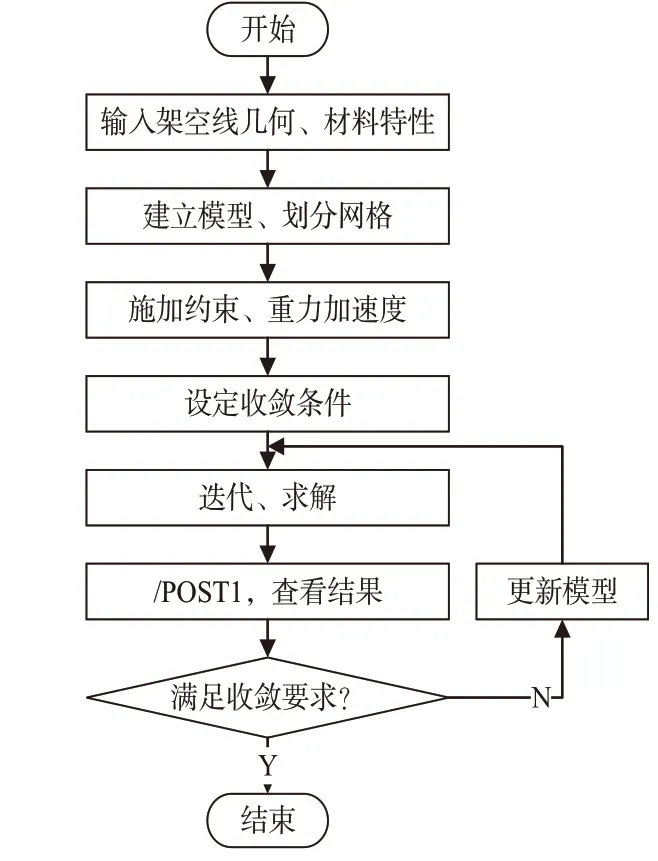
图2 找形流程图

3 输电线脱冰跳跃动态特性分析

下面以某架空输电线为例研究输电线脱冰跳跃特性，导线采用2×LGJ-400/35，其物理参数如表1所示。

表1 输电线的物理参数

3.1 水平档距大小对输电线脱冰的影响

水平档距是指相邻两杆塔之间的水平距离，由于水平档距的大小是影响脱冰跳跃高度最直接的因素，文中详细研究了不同水平档距对脱冰跳跃的影响。在不考虑高差的情况下，假定输电线上单位冰载荷为20 N/m，100%脱冰，得到结果如图3至图5所示。

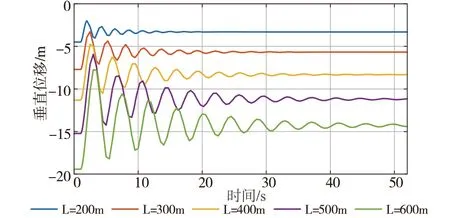
图3 不同水平档距的跨中Z向位移时程曲线

图4 不同水平档距的跨中Z向位移大小

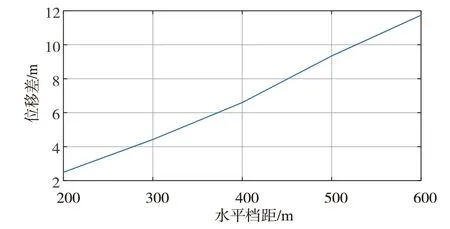
图5 不同水平档距的跨中Z向位移差值

根据图3的跨中Z向位移时程曲线图可以看出不同档距对输电线脱冰跳跃具有显著的影响。由图4可知，随着水平档距的增大，输电线的弧垂逐渐增大。此外，输电线脱冰后的跳跃高度是随水平档距近似线性增长，如图5所示。

3.2 覆冰厚度与脱冰跳跃的关系

针对不同地区之间的气温具有一定的差异，这就可能导致其输电线上的覆冰重量也不同。本案例采用集中质量法对输电线上施加冰载荷，在水平档距为500 m的情况下，分别研究了覆冰厚度为5 mm，10 mm，15 mm，20 mm，25 mm，30 mm下的导线脱冰跳跃动态特性（100%脱冰）。其中图6的负值表示其跳跃高度处于导线悬挂点（水平面）上方。

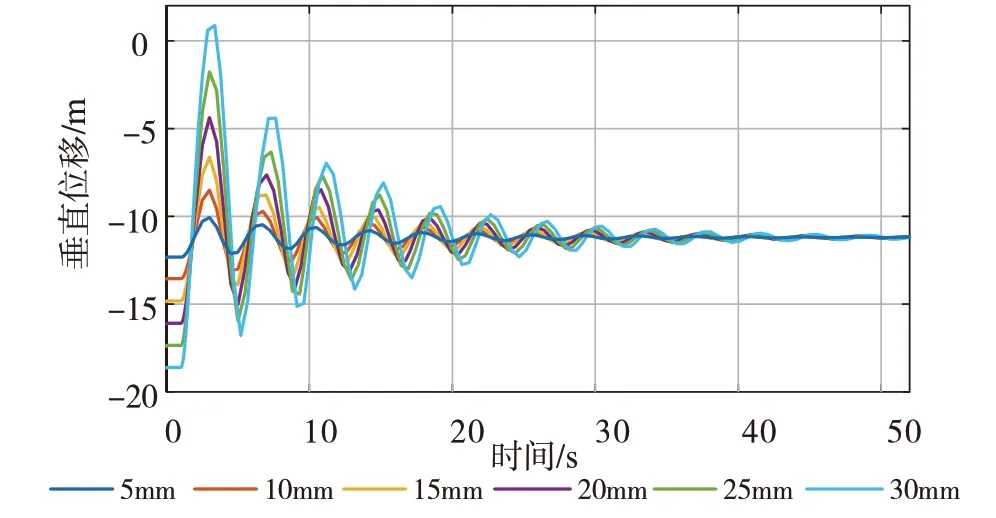
图6 不同覆冰厚度的跨中Z向位移时程曲线

从图7可以看出脱冰后跨中Z向振动幅度是随着导线的覆冰厚度的增大而变大，这一点从图7中垂向位移的最大值和最小值可以更加直观地看出。从图7还可以看出，当导线的覆冰厚度过大时（如重冰区），脱冰后的跳跃高度会超过导线悬挂点。此外，图8的结果显示导线脱冰后的振动幅度是随着覆冰厚度近似线性增长。

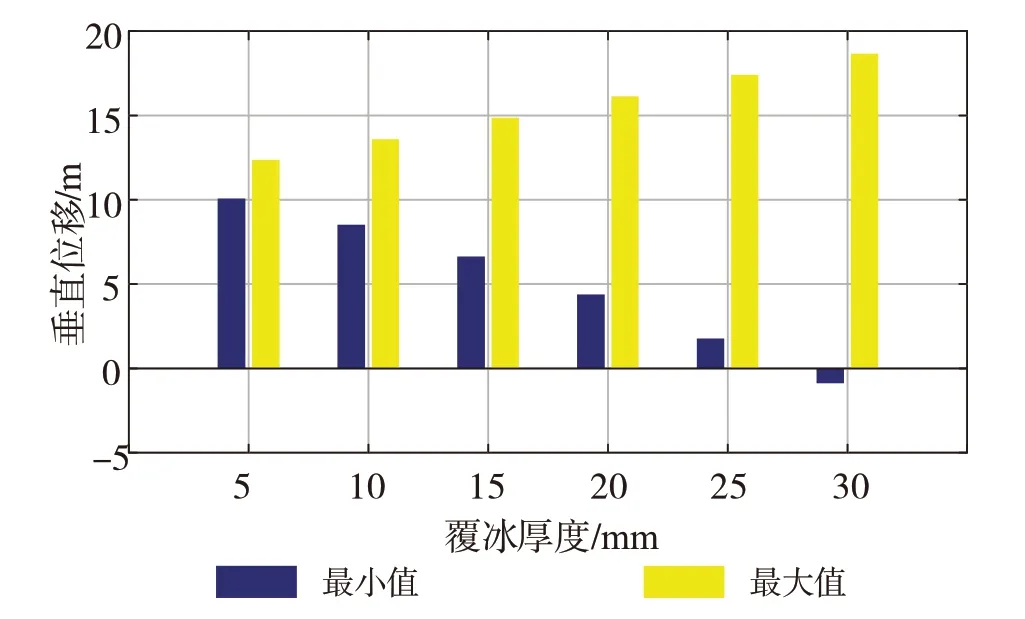
图7 不同覆冰厚度的跨中Z向位移大小

图8 不同覆冰厚度的跨中Z向位移差值

3.3 脱冰位置与脱冰跳跃的关系

考虑到输电线上的冰载荷通常不是100%脱冰，因此本案例研究了脱冰位置与导线脱冰跳跃的关系。假定水平档距为500 m，覆冰厚度为20 mm，20%脱冰，脱冰位置为图9所示。由于位置1、2与位置4、5是对称的，故而只需要研究其中一个即可。本案例以位置1、2和3为研究对象进行相关的仿真分析，得到的结果如图10至图12所示。

图9 输电线上脱冰位置

图10 不同脱冰位置的跨中Z向位移时程曲线

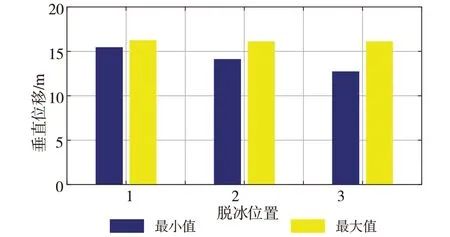
图11 不同脱冰位置的跨中Z向位移大小

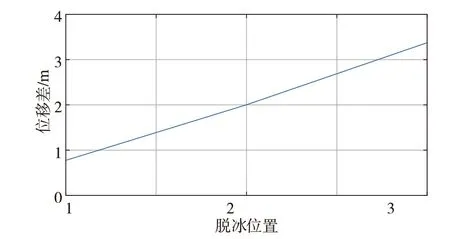
图12 不同脱冰位置的跨中Z向位移差值

由图12可知，位置3对跨中Z向位移的变化最大，其次是位置2，影响最小的是位置1。主要原因是观测点（跨中）恰好落在位置3上，且距离位置1最远。从图11、图10可以看出，针对跨中Z向振动幅度，不同位置脱冰产生的差异在1～3 m之间，可以知道不同位置的脱冰对跨中Z向的位移影响较小，且彼此之间的差异不大。

4 结语

文中针对架空输电线的特性，结合有限元理论，建立ANSYS仿真模型，研究了架空输电线路导线脱冰跳跃特性。得到如下结论：

1）架空输电线的水平档距和覆冰厚度对输电线跨中Z向位移影响显著，而脱冰位置则相对来说很小。故重冰区线路应尽量避免出现大档距。

2）在其他条件不变的情况下，输电线脱冰后的跳跃高度随水平档距（或覆冰厚度）增大近似线性增长。

3）需要注意的是当覆冰厚度足够大时，其脱冰跳跃的最高点会落在导线悬挂点的上方。