基于随机机器故障的柔性作业车间动态调度

尤一琛， 王 艳， 纪志成

(江南大学 物联网技术应用教育部工程研究中心， 江苏 无锡 214122)

柔性作业车间调度问题(flexible job-shop scheduling problem，FJSP)作为作业车间调度问题(job-shop scheduling problem,JSP)的一个扩展，在实际生产调度应用中具有更高的适用性，更加贴合实际生产调度.生产调度的任务就是把有限的资源在合理的时间内分配给不同的任务，以满足1个或多个目标[1].针对调度问题，群体智能算法和进化算法为求解FJSP提供了解决方案，然而在实际工业生产中，由于调度环境的不确定性，调度问题具有复杂性和灵活性的特点，生产环境的复杂性会使得FJSP求解难度大大提高.机器的故障及人为原因的误操作在实际生产中都不可避免，当出现该类问题时，整个车间的工件工序安排和机器安排都会出现问题，因此为了更加贴合实际中的生产过程，对于动态柔性作业车间调度问题(dynamic flexible job-shop scheduling problem，DFJSP)的研究也更有意义.

S. Z. MELISSA等[2]针对DFJSP提出了1种基于人工蜂群算法(artificial bee colony，ABC)和OSMA(operating sequence and machine assignment)双层编码的启发式算法模型框架，针对编码进行优化，采用ABC对工序编码进行优化，在机器编码中引入本地搜索进行优化，针对生产时间的变化，实现动态调度.GAO K. Z.等[3]针对FJSP中存在的机器恢复问题提出了一种改进的Jaya算法，在调度过程中，对于最大完工时间引入本地搜索启发式，在重调度过程中，引入本地搜索从而改善Jaya算法的收敛时间，并且有效平衡了重调度过程中的稳定性.ZHANG S. C.等[4]针对车间中存在的各种动态扰动问题，提出了一种启发式多智能体系统与蚁群优化算法混合的新算法，并且针对动态调度问题，提出了一种析取与或图.刘乐等[5]针对开放式车间中所存在的机器故障等问题进行了分类，并且针对各分类对其重调度方法进行了研究，提出了重调度指标，提高重调度效率.吴秀丽[6]提出了一种基于多目标免疫遗传算法，采用事件和周期混合驱动的动态调度策略来解决车间动态调度问题，并分析了算法复杂度以及影响算法复杂度的因素.

综上所述，现如今对动态调度的研究只局限于针对算法的改进，在发生故障后采用完全重调度方法或者右移重调度，并未考虑到是否需要进行重调度或者是忽略对重调度方法的选择与对比.因此，针对随机设备故障的柔性作业车间动态调度需要设计有效的重调度方法和策略.笔者采用事件驱动和周期驱动混合驱动的组合重调度策略，采用优化精英选择策略的遗传算法，并验证算法求解在随机机器故障下的动态柔性作业车间调度问题的实用性.

1 问题描述

1.1 柔性作业车间调度模型

柔性作业车间调度问题可分为机器分配问题和工序排列问题.在机器分配问题中，每道工序拥有1个或多个加工机器可选，针对不同的加工机器，在不同加工机器上的加工时间也不相同.在工序排列问题中，工序序列将取决于每台机器所选择的工序的顺序.动态柔性作业车间调度问题在柔性作业车间调度的基础上引入扰动因子，干扰主要来源有机器的故障、人为原因误操作和加急订单等，笔者引入随机机器故障为扰动因子.DFJSP可以定义如下：n件待加工工件编号分别为J1、J2、…、Jn，m台可供选择的加工机器编号分别为M1、M2、…、Mm，每个工件都有j道工序，每道工序都必须从机器集合中选择1台可加工机器，考虑到扰动因子，在随机时刻，随机机器发生故障.调度的任务是需要对n件工件的工序进行合理安排，将其以调度优化目标性能为指标分配给每台加工机器.

为了使得DFJSP调度问题规范化，需要满足以下假设条件：① 零时刻所有机器都处于待机状态；② 所有工件的工艺顺序不可发生改变，即工序的先后顺序不可逆；③ 出现扰动因子，即机器发生故障时，在该台机器上直接受到影响的工序停止加工，其他机器上未受到影响的并且正在加工的工序继续加工直到加工完成；④ 机器故障后可恢复且恢复时间可预测；⑤ 每个工件在固定时刻只能在单个机器上加工；⑥ 各工序加工时间包括加工时间和相关准备工作时间.

1.2 DFJSP的调度目标

主要研究以最小化最大完工时间为优化目标的动态柔性作业车间调度问题，计算公式为

(1)

式中：tmax为最大完工时间；ti为工件i的完工时间.

最大完工时间越小，说明调度结果的性能越好，车间生产效率越高，因此在优化目标上针对最大完工时间实现DFJSP优化.

2 精英选择遗传算法设计

2.1 编码解码

2.1.1编 码

DFJSP模型与FJSP模型类似，都由机器分配(machine assignment, MA)和工序排列(operation sequencing，OS)2个子问题构成.因此采用OSMA双层编码，分别对机器和工序进行编码，获得2段有序基因序列，得到柔性作业车间的排产方案.OSMA编码如图1所示，其中：图1a方框中数字为工件序号；Oij为工件i的第j道工序；图1b方框中数字为机器编号.

图1 OSMA编码

2.1.2解 码

针对产生的染色体，需要进行解码，从而获得有序的调度表，产生调度方案.针对图1所对应的染色体采用左移解码[2]，获得3×3的调度问题[7]的调度表，如表1所示.

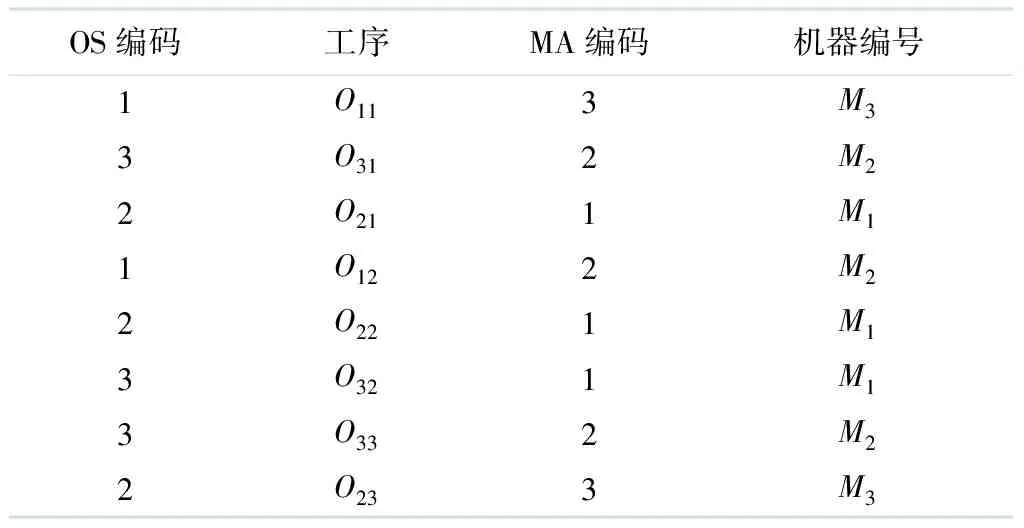
表1 调度表

2.2 精英选择策略改进

精英选择遗传算法(elite selection genetic algorithm, ESGA)[8]的定义是在基本遗传算法的基础上，在选择操作处引入精英选择策略.精英选择策略是通过对染色体适应度进行排序，保留染色体中具有最优适应度的个体，将其原封不动地保留至子代染色体中，这就使得遗传算法具有全局收敛性，但缺点是容易陷入局部最优，因此，在精英选择策略基础上，为了提高父代种群多样性，防止陷入局部最优，算法早熟，引入一个随机分布函数，即

ni=rand(0.8,1.0)Fi，

(2)

式中：ni为从Fi中选择的个体数；Fi为父代染色体经过适应度排序精英选择后的个体总数；rand(0.8,1.0)为在区间(0.8,1.0)内取随机数.

改进后的精英选择策略如图2所示.其中：Pt为父代染色体种群；Pt+1为精英选择后的子代个体集合；Qt为子代染色体种群；Qt+1为由父代形成的新的子代染色体种群.

图2 改进后的精英选择策略

2.3 交叉操作

由于编码方式为OSMA的双层编码，因此交叉操作需要分为工序排列基因段OS的交叉和机器分配基因段MA的交叉.工序排列基因段的交叉采用IPOX(improved precedence preserving operation crossover)交叉，机器分配基因段的交叉采用MPX(multipoint preservative crossover)多点交叉[9].

2.3.1IPOX交叉操作步骤

将工件集合{J1,J2,…,Jn}随机生成2个非空工序集Q1和Q2，将父代P1包含Q1的工件基因复制至子代C1中，不改变其位置，将P2中不包含Q1的工件基因按顺序复制至子代C1中的空余位置，生成C1.同理，将父代P2中包含Q2的工件基因复制至C2中，不改变其位置，将P1中不包含Q2的工件基因按顺序复制至子代C2中的空余位置，生成C2.IPOX交叉过程如图3所示.

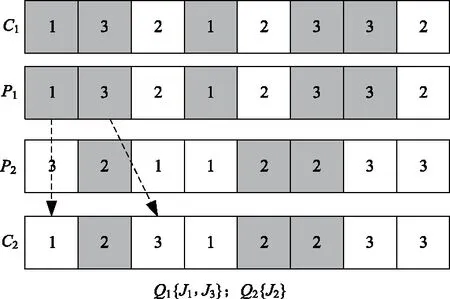
图3 IPOX交叉过程

2.3.2MPX交叉操作步骤

随机生成1个与机器编号染色体长度相同的[0，1]集合，0表示该位置处的染色体不需要交换，1表示将该位置处的染色体与上一个1位置处的染色体进行交换.

2.4 变异操作

变异操作能够防止算法早熟，并且提高局部搜索能力和维持染色体群体多样性，针对工序编码和机器编码2段染色体的变异，随机选择父代染色体中的2个基因片段，进行位置交换，得到子代染色体.

2.5 ESGA算法的流程

ESGA算法流程如图4所示.

图4 ESGA算法流程图

3 DFJSP分析

重调度分为2个方面的问题：① 何时开始重调度，即重调度的驱动策略；② 如何进行重调度，即重调度的方法.

3.1 重调度评价指标

3.1.1完工时间偏差

在完成重调度后，得到新的完工时间，引入完工时间偏差，来计算发生扰动并重调度后产生的影响.采用完工时间之差的方式进行评价，完工时间之差为

(3)

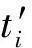
3.1.2序列偏差

工件工序的偏差将产生移动工序所需要的人工成本和材料调运成本，因此引入序列偏差作为评价指标，针对对应工序的机器变更进行评价.

由式(4)判断工件i的工序j加工机器是否发生改变.

(4)

生成评价指标SD，即

(5)

式中：num(j)为总工序数.

因此整体的重调度评价指标为

Y=ω1tD+ω2SD，

(6)

式中：ω1和ω2为权重值，且ω1+ω2=1.

重调度评价指标越小越好.

3.2 重调度驱动策略

3.2.1基于事件驱动重调度

基于事件驱动重调度是根据是否有动态扰动事件的发生来决定是否启动重调度，这种驱动机制具有良好的实时性，能够实时响应扰动事件，然后做出实时决策，但是若遇到连续频繁的扰动事件，那么其系统的稳定性会降低，计算的复杂性将会大大提高.

3.2.2基于周期驱动重调度

基于周期驱动重调度是通过设立1个周期来使得整个系统按照一定频率进行重调度.这种驱动机制有效避免了对系统稳定性的影响，其稳定性较好，且在实际应用中较容易实现，但是若遇到突然扰动事件，其响应速度较慢，并且无法选择合理的周期值.

3.2.3基于事件和周期混合驱动重调度

采用基于事件和周期混合驱动重调度，将事件驱动和周期驱动结合在一起来驱动重调度，能够在保证系统稳定性的同时，也能够响应突发动态时间，从而更加有效地提高了系统的稳定性[10].

3.3 重调度方法

以随机机器故障为扰动因素，建立了DFJSP模型，在该模型的基础上作如下假设：在tf时刻处，机器BM发生故障，预计需要恢复的时间为tr，此时在该机器上进行加工的工序为Oij，且所有工序的加工时间和加工顺序都是已知且固定的.

3.3.1右移重调度

传统右移重调度是将在发生故障时，所有受影响工序的加工开始时间向后推移tr个时间单位，以适应突发扰动所造成的影响，并且确保后续工序可以正常运行.此方法虽然稳定性较好，但是由于所有受影响的工序开始时间都被推后固定时间，则其最大完工时间将大大提高，影响生产效率.因此针对这种情况，为实现部分重调度，设计了一种二叉树右移重调度方法，二叉树的起始根部为Oij，左子树用来存放根部工序后续受到影响的工序，右子树用来存放在机器k上受到影响的其他工件的工序，该方法的步骤如下：

1) 二叉树起始根部受影响的工件工序为Oij，找到未开始的工序集合O′.

2) 根据不等式(7)，在O′中，筛选出当前受影响工件的左子树上的工序集合.若满足不等式(7)，则将该工序加入当前左子树，并根据式(8)和式(9)更新该工序后续工序的开始时间和完工时间.

tr+tijk>tsi(j+1)k′，

(7)

tsi(j+1)k′=tr+tijk，

(8)

ti(j+1)k′=tpi(j+1)k′+tsi(j+1)k′，

(9)

式中：tijk为工件i的第j道工序在机器k上的完工时间；k为故障机器编号；k′为预调度方案中工序的加工机器；tsi(j+1)k′为工件i的第j道工序的下一道工序在机器k′上的开始时间；ti(j+1)k′为工件i的第j道工序的下一道工序在机器k′上的完工时间；tpi(j+1)k′为工件i的第j道工序的下一道工序在机器k′上的加工时间.

3) 根据不等式(10)，对步骤2)中所产生的左子树上的工件集合进行迭代，筛选出当前受到影响工序的右子树上的工序集合，并且剔除左子树中已有工序，保证左子树与右子树中的工序不重叠，若满足不等式(10)，则将该工序加入对应的右子树，并根据式(11)和(12)更新该工件的开始时间和完工时间.

tr+tijk>tsj′k，

(10)

tsj′k=tr+tijk，

(11)

tj′k=tpj′k+tsj′k，

(12)

式中：tsj′k为该工序在同一台机器k上的下一道工序j′的开始时间；tj′k为该工序在同一台机器k上的下一道工序j′的完工时间；tpj′k为该工序在同一台机器k上的下一道工序j′的加工时间.

4) 遍历步骤3)中新产生的右子树中的工序，对其进行步骤2)的操作，直到循环至O′中的工序循环才完毕.

采用1个3×3算例[11]，采用上述改善后的部分右移重调度，假设O21加工完成时机器M1故障，得到基于二叉树的右移重调度示意图如图5所示.

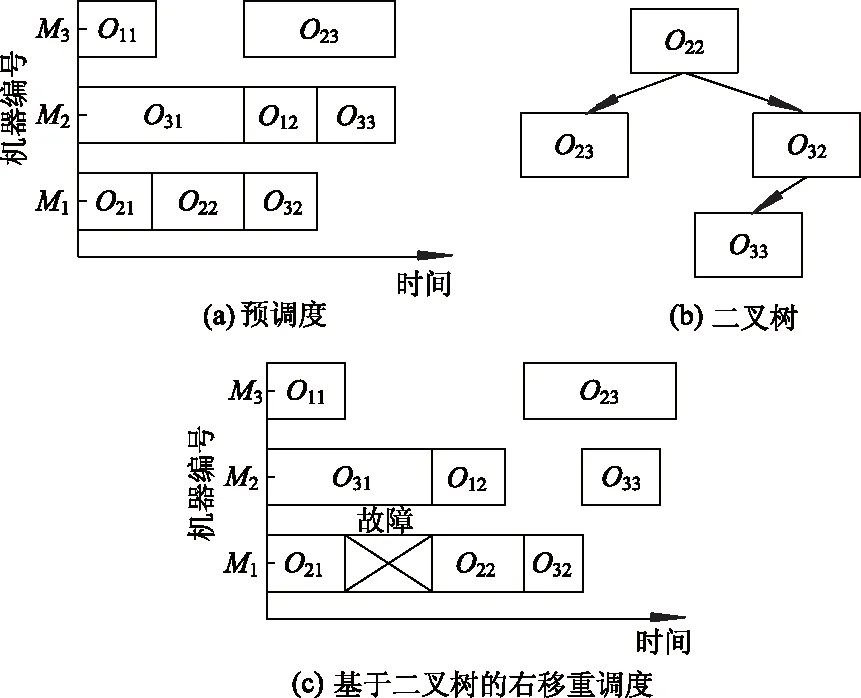
图5 右移重调度示意图

3.3.2完全重调度

采用基于未开工工序的完全重调度，在机器发生故障后，为了重调度得到更优的最大完工时间或者消除机器故障对生产时间造成的影响，对在tf时间后才开始加工的工序进行重调度，原先已完成或者正在加工的工序序列和机器分配均不改变，得到新的重调度方案.

3.3.3组合重调度策略

根据式(6)设计了一种组合重调度策略，基于重调度评价指标，将右移重调度与完全重调度相结合，采用重调度评价指标来评价右移重调度与完全重调度所生成的方案的表现，最后采用重调度评价指标较低的重调度方案.

3.4 重调度流程

重调度流程如图6所示.

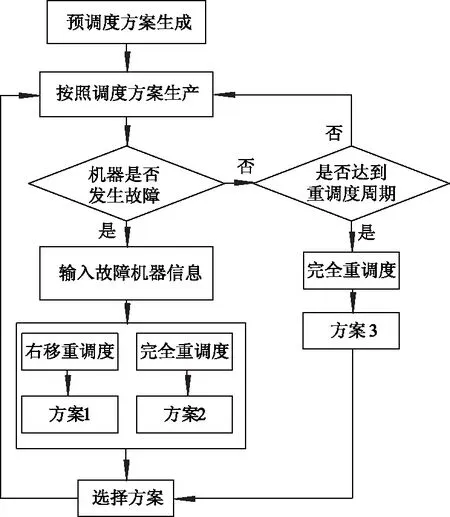
图6 重调度流程图

4 试验结果及分析

采用MATLAB R2019b软件针对动态柔性作业车间问题进行仿真，电脑硬件参数如下：处理器为Intel(R) Core(TM) i5-8500 CPU @ 3.00 GHz；内存为8 GB.

4.1 试验设置

4.1.1试验算例设置

采用6×6×10实例进行仿真测试，该算例含有6个工件，每个工件含有6个工序，共有10台机器[11]，仿真数据如表2所示.

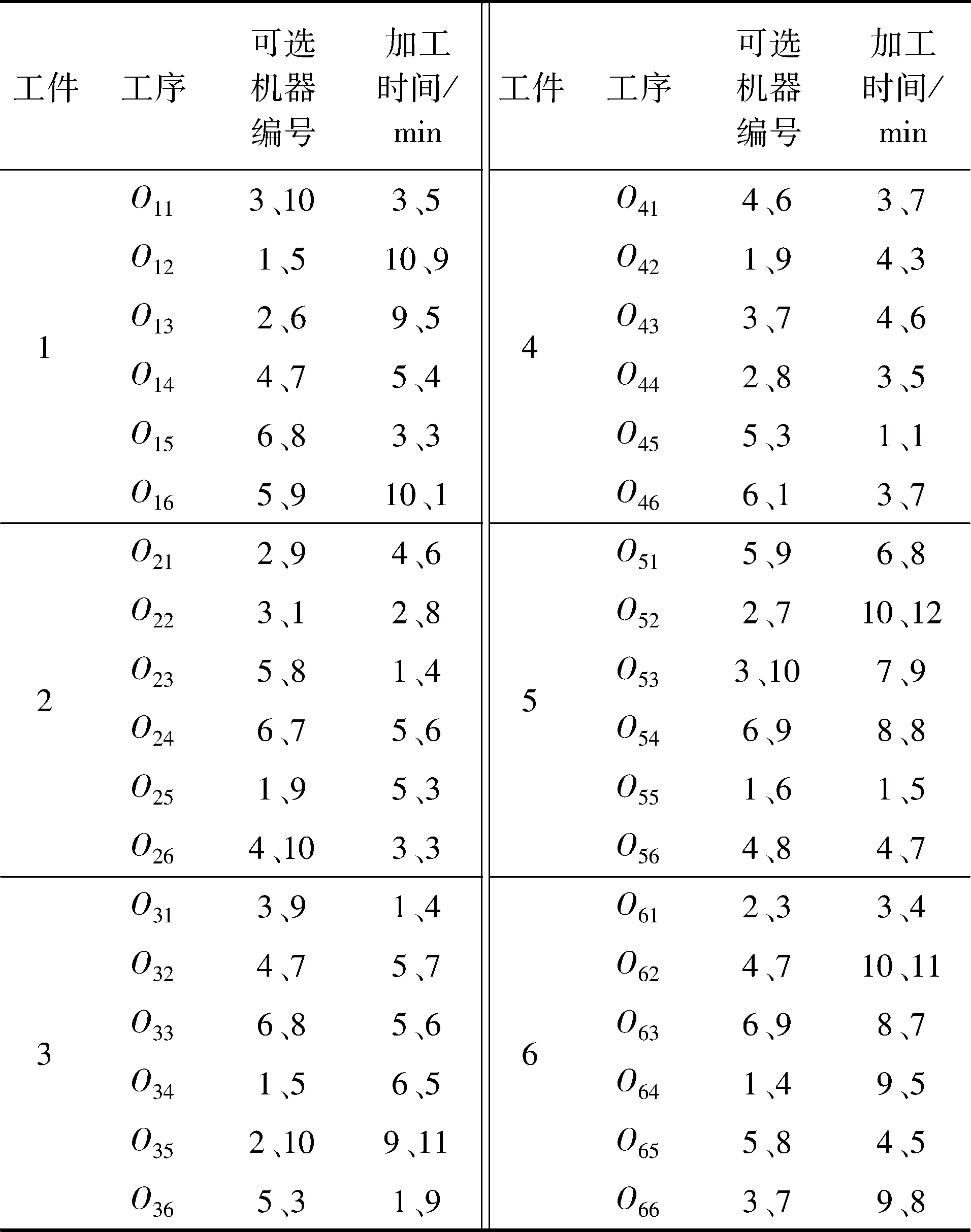
表2 仿真数据集

4.1.2ESGA算法参数设置

ESGA算法中，群体规模为50，编码长度为36，迭代次数为100次，交叉概率为0.7，变异概率为0.1.

4.2 试验仿真分析

针对随机机器故障的柔性作业车间调度问题，选定重调度评价指标的权重为0.9和0.1.随机设置第4台机器为故障机器(BM=4)，在第13 min发生故障，预计需要5 min恢复正常工作状态.

图7为生成的预调度方案，其最大完工时间为43 min.

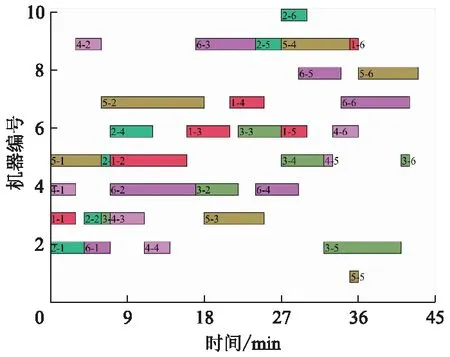
图7 预调度甘特图

当机器4在第13 min发生故障，仿真得到的右移重调度甘特图如图8所示，其最大完工时间为48 min.

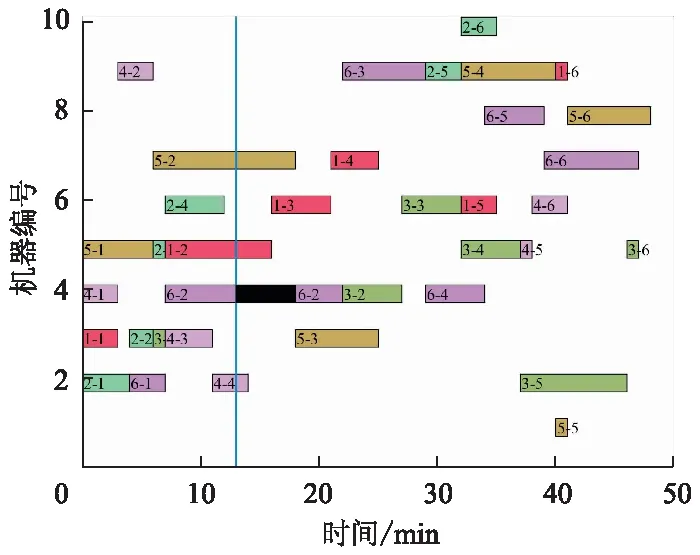
图8 右移重调度甘特图(BM=4)

从图8可以看出：在故障发生后，考虑恢复时间，仅仅针对受到影响的未完成工序进行右移重调度，而不是将所有未完成的工序均进行右移动重调度，并且将工序排序更为紧凑，有效地降低机器故障对整体生产稳定性的影响.

图9为完全重调度方案，其最大完工时间为47 min，相比右移重调度，在优化最大完工时间程度上，完全重调度性能表现更优.

图9 完全重调度甘特图(BM=4)

通过计算2种方案的重调度评价指标，完全重调度的评价指标为3.9，小于右移重调度的评价指标4.5，分析可知，虽然完全重调度需要对工序的机器进行调整，影响了整体生产的鲁棒性，但是在综合方面指标来看，完全重调度所得的方案性能表现更优，因此，组合重调度策略最后选择完全重调度方案.

设置第3台机器BM=3在第19 min发生故障，预计需要6 min恢复正常.图10为右移重调度生成的调度方案，其最大完工时间为47 min.

图10 右移重调度甘特图(BM=3)

从图10可以看出：只针对部分受影响的工序进行右移，并且右移量并非仅仅取决于恢复所需要的时间，而且还需要根据机器和工序间隙来决定受影响工序的右移量.

图11为完全重调度生成的调度方案，其最大完工时间为44 min，其有效降低了机器故障所带来的影响.通过计算评价指标，组合重调度策略选择完全重调度方案.

图11 完全重调度甘特图(BM=3)

为了验证算法的有效性，随机设置3组故障机器情况(3、4、5)，分别采用右移重调度，完全重调度和组合重调度策略进行10次仿真试验，对数据求平均值，结果如表3所示，在故障恢复时间较长的情况下，完全重调度的表现优于右移重调度，右移重调度在故障恢复时间较短的情况下表现更优，并且，相比于右移重调度和完全重调度，在发生机器故障时，采用组合重调度可以更加有效地降低机器故障对整个生产过程中带来的影响，验证了组合重调度策略的有效性.

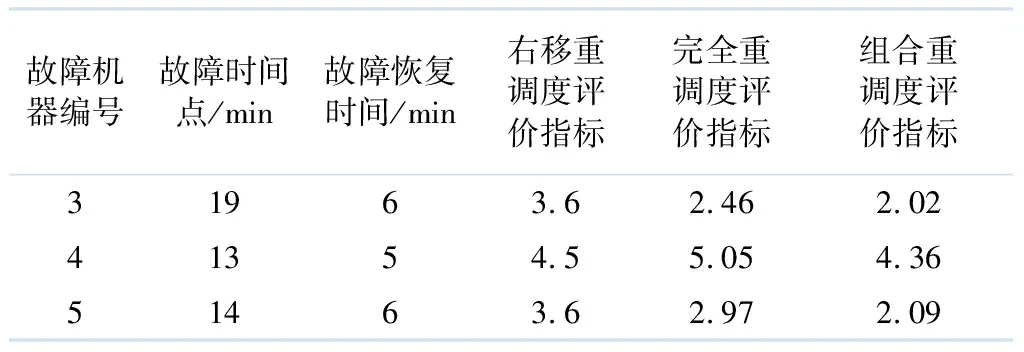
表3 仿真结果对比

5 结 论

针对FJSP中发生随机机器故障的动态事件，改进了含有精英策略的遗传算法，并设计了一种部分右移重调度，采用二叉树，对右移时间量与右移工件进行计算筛选，减少生产系统受到的影响.同时，将右移重调度与完全重调度相结合，引入重调度评价指标，设计了一个组合重调度策略，对动态调度过程中右移重调度和完全重调度的方案进行评价选择，实现对柔性作业车间中机器故障情况下的动态调度，通过与右移重调度和完全重调度的对比，可以得出如下结论：组合重调度策略能够有效改善机器故障发生后柔性作业车间动态调度的最大完工时间和机器偏移量.通过仿真试验，验证了动态调度算法对解决随机机器故障下柔性作业车间动态调度问题的有效性.