基于三角模糊数的不完全信息静态库诺特博弈模型及其应用
赵洪斌,陈奕延
(1.中咨工程管理咨询有限公司,北京 100048;2.北京理工大学 管理与经济学院,北京 100081)
一、引言
随着科技水平的不断发展,人类对精确性分析的需求与日俱增,大数据、云计算、深度学习等一系列新型技术都是为满足这类需求而产生的。然而,与精确性分析相悖的模糊性分析也随之蓬勃发展,模糊数学在处理实践中的某些问题甚至优于传统的经典数学方法[1],与此同时,近些年的诺贝尔经济学奖有多次都颁发给了研究博弈论或博弈论相关方向的学者,包括Alvin E.Roth(2012)、Jean Tirole(2014)、Oliver Hart(2016)和Bengt Holmstrom(2016)等人[2],这无疑激起了许多学者研究博弈问题的兴趣,中国作为模糊数学研究的四大中心(美国、西欧、日本、中国)之一,自然而然出现了许多交叉性质的学术研究,即使用模糊数学来研究博弈问题:李纪真等(2015)[3]针对当前网络安全预警响应决策模型缺乏主动性且未引入响应时机决策机制而导致无法在最佳时机触发最优响应策略的问题,建立了基于双重动态非对称三角模糊矩阵博弈的主动预警响应决策模型,该模型生成的方案可以使攻击者在扫描、漏洞溢出、权限提升三个阶段的最低收益分别降低28.4%、11.6%和2.6%,提高了网络安全主动预警响应决策能力和效率;李翠和薛惠锋(2016)[4]基于模糊联盟博弈模型,对模糊博弈的核心解及稳定集解进行梳理,报告了博弈核心解在企业知识联盟利益分配中可能为空集的现状,通过采用引入隶属度及分配系数的方法,展开广义模糊解概念的延拓、广义模糊解间关系的刻画及模糊联盟博弈收益值部分保留的需求调查,反映了既能满足企业与多个知识联盟合作又可满足企业知识联盟再发展的应用需求问题;李瑾(2016)[5]基于模糊合作理论,进而建构了联盟博弈模型并以供应链为考察视角,对该博弈模型作出了两次模型拓展与应用,以期为信息时代下物联网的发展及其相应的物流管理提供理论指引与经验证据;孙蕾和孙绍荣(2017)[6]构建了跨域合作污染治理的特征函数及模糊合作博弈的参与度函数,结合京津冀实际环境数据,利用模糊博弈Shapley 值法获得合作省市成本分摊方案,最后分析了年平均浓度,年空气质量未达标天数及环境污染治理力对成本分摊值的影响关系;孙红霞和张强(2017)[7]针对参与联盟的局中人具有一定参与度的情形,研究了具有模糊联盟的双合作博弈的支付分配问题,通过成本分摊算例验证了模糊双合作博弈支付分配模型的可行性;苗治平和李翠(2017)[8]构建了模糊平均单调博弈模型,通过博弈模型的求解来解决合作联盟最优利益分配问题。诸如此类的研究有很多,却较少有研究模糊条件下库诺特博弈模型及其均衡解的成果。
二、知识准备
满足定义[9],且隶属函数图形如图1 所示的模糊数称为三角模糊数,其中l,m,r沂R,l,r 分别称为三角模糊数的下界和上界,m 称为三角模糊数的主值,(m-l)与(r-m)称为三角模糊数的下限和上限,当l=m=r 时,三角模糊数退化成普通的经典实数,(r-l)的值越大,越模糊。

图1 三角模糊数
u(x)为隶属函数,L(x)为左隶属函数,R(x)为右隶属函数,0臆L(x),R(x)≤1,其隶属函数的表达式为:

该式通常可省略0 值部分,其简式为:

若加之限定条件,令l,m,r>0,则此时的三角模糊数称为正三角模糊数,如图2 所示。

图2 正三角模糊数
正三角模糊数的表达式同公式(1)与公式(2)一致,表示方式也与三角模糊数一致,在经济问题中由于变量和参数通常为正数,故多使用正三角模糊数来解决相关问题。
三角模糊数的运算性质可参考张兴芳等(2005)[10]的论文与李荣钧(2002)[11]的著作。特别注意,两个三角模糊数的乘积不再是三角模糊数,如图3 所示。

图3 两个三角模糊数及其乘积
其中N1与N2是三角模糊数,亦是一个正模糊数,但非三角模糊数。
三、模型构建
库诺特博弈模型常被用来研究市场的双寡头垄断竞争,其定义和具体介绍可参考相关文献[12-14],模型假设厂商之间不存在任何正式或非正式的勾结,且每一方都知道对方将如何行动,库诺特博弈模型也常被运用于研究各类假设条件下的博弈问题,这其中较为复杂的是不完全信息静态库诺特博弈模型,这里引入正三角模糊数,假设两企业生产同类同质的产品,企业1(记为E1)和企业2(记为E2)均有高、低两种类型的模糊单位成本,企业1 和企业2 彼此不知道对方的模糊单位成本,只具有信念,企业E1 和企业E2 生产相同的产品,相关变量如表1 所示。

表1 模糊单位成本及信念
可知,企业E1 和企业E2 的高低成本均是正三角模糊数,lij,mij,rij>0[15],按照三角模糊数之间比较大小的方法,则单位模糊成本的高低(大小)必须满足表2 所述条件。

表2 三角模糊数大小条件表
其中,三角模糊数M(Nij)的均值为:

设其方差为σ2(Nij),则方差表达式为:
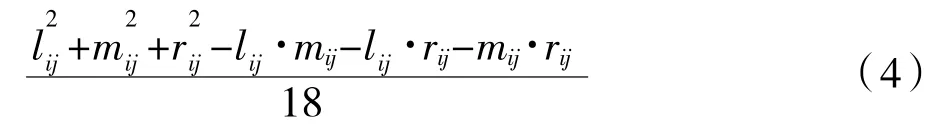

(一)完全垄断的模糊最优产量

由于有4 种模糊成本,故相应的模糊垄断利润亦有4 种,其模糊收益函数的表达式可由联立方程组得到:



由模糊最优产量可得两个企业的行动空间的表达式为:


(二)模糊贝叶斯均衡产量

对其中4 个最优化问题的决策变量求导,并令导数等于0,可得以下联立方程组:

对方程组进行整理,求解过程参考经典实变量情况下的方法[16],分别解得4 种模糊单位成本下的模糊贝叶斯均衡产量:

四、算例演示

由公式(3)及公式(4)判断可知表3 中的模糊单位成本满足表2 中的条件,计算两个企业E1 和E2 的模糊贝叶斯均衡产量,省略计算步骤,将最终计算结果在表4 中列出。

表3 模糊单位成本及信念

表4 计算结果表


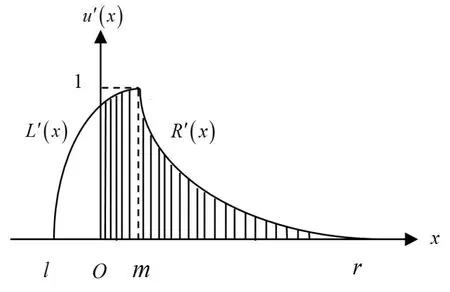
图4 改进型模糊数
五、结语
基于三角模糊数的不完全信息静态库诺特博弈模型可有效求解双寡头企业在不完全信息条件下参量模糊的贝叶斯模糊均衡产量,其运用的模糊博弈的方法可以解决模型中参量模糊的博弈问题,为今后进一步研究模糊博弈或不确定性(概率、模糊数学、灰色系统、粗糙集等)博弈问题提供了参考依据。未来可从以下三个方向进行深化研究。
首先,将机器学习与模糊博弈结合,在预测、分类、聚类算法的基础上,将博弈模型作为内生约束条件嵌入,从而在决策计算中纳入利益分配机制的考量,以便于处理海量信息决策时的利益分配问题;其次,可考虑正态模糊数等其他模糊数的博弈模型,杜绝三角模糊数“尖点突变”的缺陷;最后,可建立更为宏观的算例库,针对不同社会经济问题开展更多实证类研究,通过“反馈-调节”的方式进一步检验模型的实效性。

