考虑间断分布切削刃真实运动轨迹的立铣刀侧铣表面扇形残留研究
张建超,牛兴华*,孟意兵,于紫昭,王学腾
(天津理工大学a.天津市先进机电系统设计与智能控制重点实验室,b.机电工程国家级实验教学示范中心,天津300384)
早在20世纪40年代,MARTELLOTTI[1-2]通过具体的实验与分析,给出了关于铣刀切削刃轨迹的明确描述,铣削加工过程中刀具切削刃的轨迹是次摆线,而不是圆弧线,并且推导出了准确的轨迹方程。目前,刀具切削刃真实运动轨迹也越来越多地被考虑到铣削过程中。贺小东等[3]通过计算铣刀切削刃的真实运动轨迹即次摆线运动轨迹,推导出未变形切削厚度计算的超越方程。通过对该超越方程的数值求解,得到了准确的未变形切削厚度。聂强等[4]通过研究刀具真实切削运动过程中的次摆线轨迹及其影响,提出一种新的瞬时切厚解析计算方法,并针对两齿和四齿的情况给出瞬时切厚的具体计算公式。窦炜等[5]利用刀具切削刃真实轨迹即次摆线,处于切削状态的刀刃与前一齿尖所经过的摆线运动轨迹相交,以其方位角与前一刀齿过同一交点时的方位角之差为辅助变量,建立了满足铣屑形成条件的运动学超越方程。MONTGOMER等[6]和ALTINTAS等[7]基于切削刃真实轨迹建立了动态铣削模型并应用于周铣过程中,以此来确定颤振对工件表面的影响。
对于真实轨迹的研究,多数学者集中在利用真实运动轨迹去研究切削厚度和利用有限元仿真去研究铣削力、铣削温度的变化规律,而对于真实运动轨迹下的铣削工件表面形貌的研究很少涉及。
零件表面形貌对于零件的表面质量以及零件的使用性能有很大的影响,很多学者对于机械加工中的表面形貌进行了大量的研究。OMAR等[8]研究了平头铣刀端铣削系统,通过Z-map法描绘出了工件表面轮廓,并获得了不同的主轴旋转状况下,零件表面形貌的变化情况。CHEN[9]在考虑切削参数的基础上,利用切削刃扫掠轨迹与工件求交,获得残留高度来预测表面形貌,同时又分析了加工过程中的动态特性。MIZUGAKI[10]针对不同姿态下的球头铣刀,对切削刃上的点进行了数学描述,并根据加工中刀具的运动,给出了工件表面形貌的解析方程,并进行了求解。
对工件表面形貌的研究,多数集中在研究两行刀轨之间的行间残留,而对铣刀回转表面上间断分布切削刃所形成的沿进给方向的扇形残留的研究极少。
本文在考虑铣刀切削刃真实运动轨迹的同时,对考虑间断分布切削刃的扇形残留展开研究。
1 铣刀切削刃真实运动轨迹
1.1 摆线及次摆线
1.1.1 关于摆线及次摆线
摆线一般是指一个基圆沿直线作无滑动的滚动时,基圆上一定点所形成的轨迹。次摆线包括长幅摆线和短幅摆线。长幅摆线是指基圆外一定点的轨迹,短幅摆线是指基圆内一定点的轨迹。
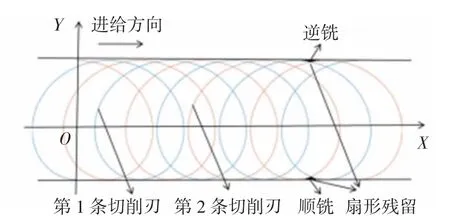
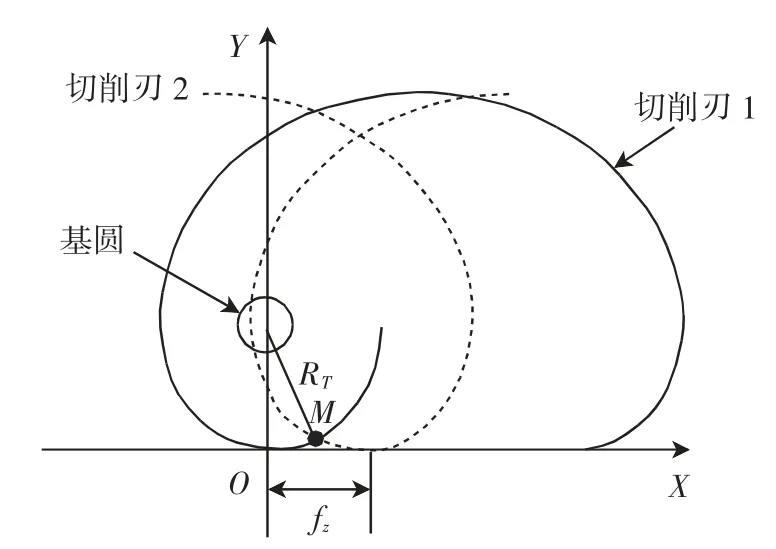
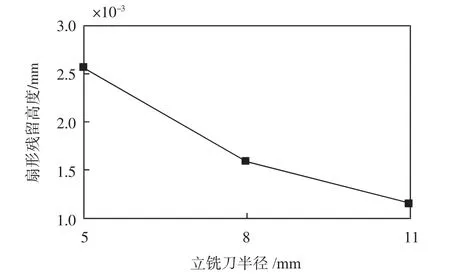
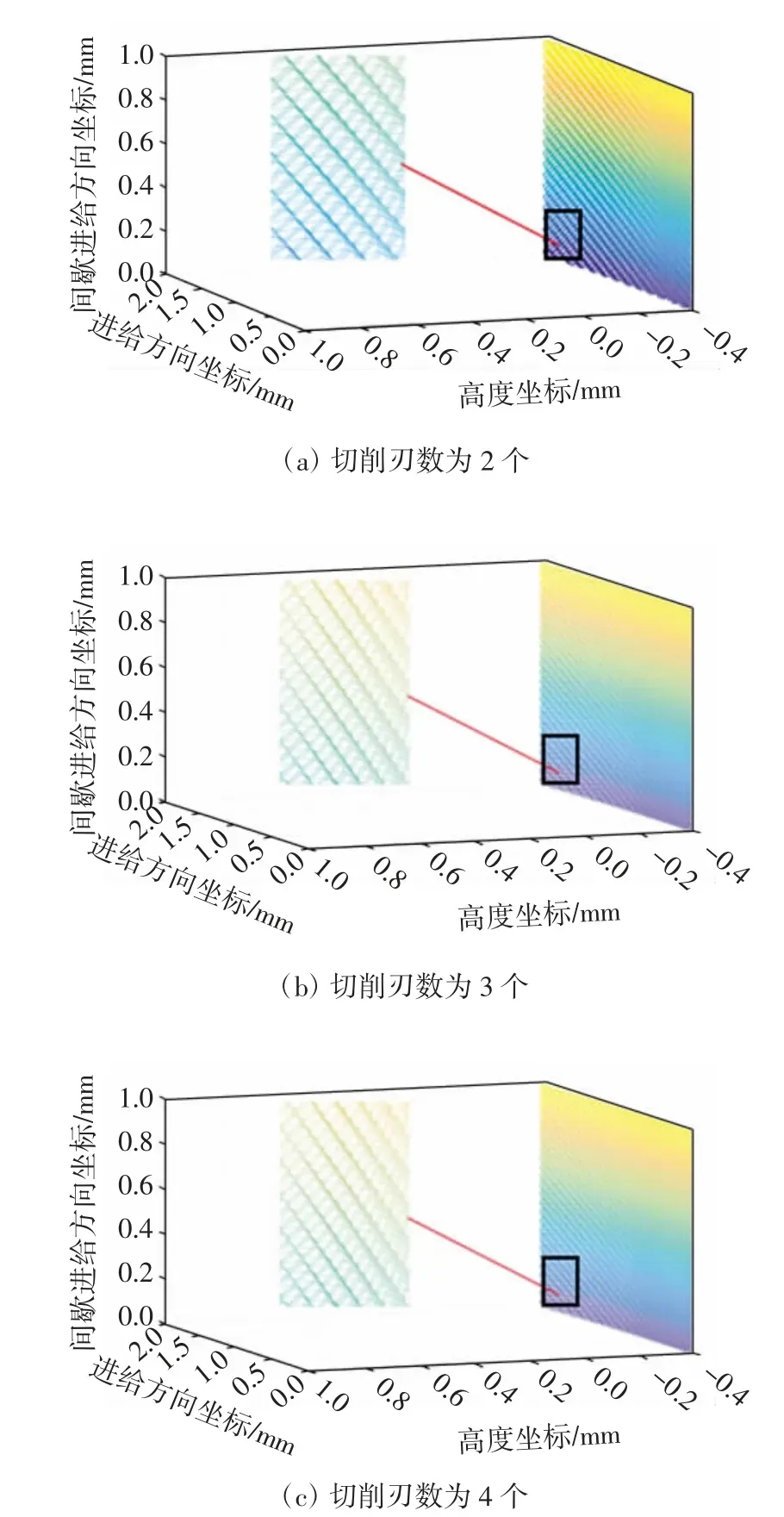
摆线和次摆线轨迹的形成如图1所示。其中X轴为与基线平行且过基圆圆心,R为基圆半径,r为某一定点与基圆圆心之间的距离。当r=R时,轨迹为摆线;当r>R时,轨迹为长幅摆线;当r 图1 摆线和次摆线轨迹的形成Fig.1 Formation of cycloid and trochoidal trajectory 1.1.2 摆线及次摆线的参数方程 将曲线表示为如下参数形式 可进一步得到 分别将式(1)和式(2)代入式(6)中,可得出摆线及次摆线的曲率。 摆线曲率K1为: 由摆线曲率的公式可以看出,随着R的增大,摆线的曲率逐渐减小。 1.2.1 切削刃运动轨迹参数方程 铣刀在实际铣削加工时,刀具的运动包括绕自身轴线的旋转运动和进给方向的平动,切削刃运动轨迹为次摆线。摆线的基圆半径为[11]: 2)逆铣时次摆线运动轨迹的曲率。当逆铣即运动轨迹的转角为φ=(2n+1)π(n=0,1,2,…)时,长幅摆线的曲率K为: 将式(11)与式(12)进行比较可知,顺铣时的曲率大于逆铣时的曲率。 3)顺、逆铣的扇形残留分析。次摆线运动轨迹及顺、逆铣如图3所示,由于顺铣时的曲率大于逆铣时的曲率,因而顺铣时工件表面的扇形残留高度大于逆铣时工件表面的扇形残留高度。 图3 次摆线运动轨迹及顺、逆铣Fig.3 Cycloid motion trajectory and up and down milling 立铣刀曲面模型如图4所示,建立与刀具固结的刀具坐标系σ0(O0-X0Y0Z0),其中Z0轴为沿着刀具主轴轴线方向。θ为刀具曲面上任意一点P在X0O0Y0平面内与X0轴夹角,RT为刀具半径。建立立铣刀的刀具曲面参数方程为: 图4 立铣刀曲面模型Fig.4 Surface model of end mill 立铣刀切削刃模型如图5所示,P′为切削刃上一点,P′在X0O0Y0平面内的投影与X0轴夹角为θ,刀具螺旋角为β,建立刀具坐标系下的切削刃曲线参数方程为[12]: 图5 立铣刀切削刃模型Fig.5 Cutting edge model of end milling cutter 立铣刀的其他切削刃可看成是由第1个切削刃旋转一定角度后形成的,多条切削刃的立铣刀参数方程为: 式中,Z为切削刃数,j为第j条切削刃,其中j∈[1,Z]。 3.1.1 不考虑切削刃时立铣刀侧铣表面 当对立铣刀侧铣表面研究不考虑刀具切削刃时,立铣刀的铣削部分是以圆柱面的形式运动。铣削运动过后所形成的加工表面是一个光滑的平面。图6为不考虑刀具切削刃的侧铣工件表面仿真结果。 图6 不考虑刀具切削刃的侧铣工件表面仿真结果Fig.6 Surface simulation results of the side milling workpiece without the cutting edge of the end milling cutter 3.1.2 考虑间断分布切削刃的侧铣表面形貌 实际铣削加工过程中,刀具存在间断分布的切削刃,铣刀切削刃真实运动轨迹为次摆线。 由于立铣刀的切削刃在回转表面存在间断分布,从而在刀具沿进给方向会有一部分材料未被刀具切削刃切除掉,从而残留在工件表面上,称为扇形残留。图7为考虑刀具切削刃的侧铣工件表面仿真结果。 图7 考虑刀具切削刃的侧铣工件表面仿真结果Fig.7 Surface simulation results of the side milling workpiece with the cutting edge of the end milling cutter 由立铣刀的真实加工轨迹为次摆线轨迹,可推导出扇形残留高度h。图8为立铣刀切削刃次摆线运动轨迹,切削刃1和切削刃2中每相邻的两个最低点间的距离即每齿进给量fz,图8中点M的高度即为扇形残留高度h。当刀具切削刃数为两个时,M点位于1/2每齿进给量处,代入公式(10)可得公式为: 图8 立铣刀切削刃次摆线运动轨迹Fig.8 Trajectory of trochoidal motion of the cutting edge of the end milling cutter 式中,RT为刀具半径,φ为刀具转角。 从而可得扇形残留高度的公式为: 仿真计算算法采用Z-map法[13],假设工件不动,由刀具完成进给运动形成工件表面。 由于MATLAB编程计算的要求,统一将立铣刀的切削刃参数方程写成齐次坐标矩阵形式为: 设刀具绕Z轴旋转角度为φ,沿X、Y、Z方向进给速度分别为vx、vy、vz,分别与进给时间相乘,即为3个坐标方向的位移分量,旋转变换矩阵表示为: 矩阵Q乘切削刃矩阵后得到切削整体坐标,再与加工前工件整体坐标进行布尔运算后,就可以得到加工后的工件表面形貌。 仿真计算中,首先在MATLAB软件中建立网格模型,将工件的表面划分为x×z个网格,根据仿真工件的大小和精度要求选取x和z。Y1表示为刀具离散点的y值,Y2表示工件高度的y值。然后将工件高度Y2赋予一个初值,本文初值为加工余量0.2 mm。根据精度要求将切削刃离散成若干个微元,由式(18)和式(19)计算出刀具离散点的值。最后与工件高度值比较,若Y1 图9 仿真计算算法流程图Fig.9 Flow chart of simulation calculation algorithm 应用MATLAB软件仿真研究时,通过改变铣刀半径和铣刀切削刃数来观察表面形貌中扇形残留的变化。 3.3.1 铣刀半径对扇形残留的影响 仿真试验铣刀参数如表1所示。立铣刀半径对扇形残留的影响如图10所示,其中图10的(a)、(b)和(c)分别对应于表1中的第1组、第2组和第3组的各项数据。 图10 立铣刀半径对扇形残留的影响Fig.10 Influence of end milling cutter radius on fan-shaped residue 表1 仿真试验铣刀参数Tab.1 Milling cutter parameters for simulation test 通过改变铣刀半径来观察表面形貌中扇形残留高度的变化。当其他量保持不变,只改变立铣刀半径时,可得到立铣刀半径与扇形残留高度的关系,如图11所示。 由图11可分析出,随着立铣刀半径的增大扇形残留高度逐渐减小。 图11 立铣刀半径与扇形残留高度的关系Fig.11 Relationship between the radius of the end milling cutter and the fan-shaped residual height 3.3.2 铣刀切削刃数对扇形残留的影响 仿真试验铣刀参数如表2所示。立铣刀切削刃数对扇形残留的影响如图12所示,其中图12的(a)、(b)和(c)分别对应于表2中的第1组、第2组和第3组的各项数据。 图12 立铣刀切削刃数对扇形残留的影响Fig.12 Influence of cutting edge number of end milling cutter on fan-shaped residue 表2 仿真试验铣刀参数Tab.2 Milling cutter parameters for simulation test 通过改变铣刀切削刃数来观察表面形貌中扇形残留高度的变化。当其他量保持不变,只改变立铣刀切削刃数时,可得到立铣刀切削刃数与扇形残留高度的关系,如图13所示。 由图13中关系可分析出,随着立铣刀切削刃数的增加扇形残留高度逐渐减小。 图13 立铣刀切削刃数与扇形残留高度的关系Fig.13 Relationship between the cutting edge number of end milling cutter and the fan-shaped residual height 本文首先提出了刀具切削刃在铣削中的真实运动轨迹,建立了立铣刀回转曲面方程和切削刃方程。然后研究了考虑立铣刀切削刃的真实运动轨迹的工件表面成形算法,比较了真实运动轨迹下顺铣与逆铣的曲率大小。接着给出了一种求解扇形残留高度的求解方法。最后通过使用MATLAB仿真软件改变立铣刀半径和立铣刀切削刃数进行仿真实验。由仿真实验结果可以得出如下结论。 1)顺铣时的曲率大于逆铣时的曲率,因而顺铣时工件表面的扇形残留高度大于逆铣时工件表面的扇形残留高度。 2)当立铣刀其他参数不变,改变立铣刀半径的大小时,随着立铣刀半径的增大扇形残留高度逐渐减小。 3)当立铣刀其他参数不变,改变立铣刀的切削刃数时,随着立铣刀切削刃数的增加扇形残留高度逐渐减小。 因此,在实际的铣削加工中采用多刃半径大的刀具会极大地改善铣削表面质量。诸上研究对零件表面质量的研究具有积极意义。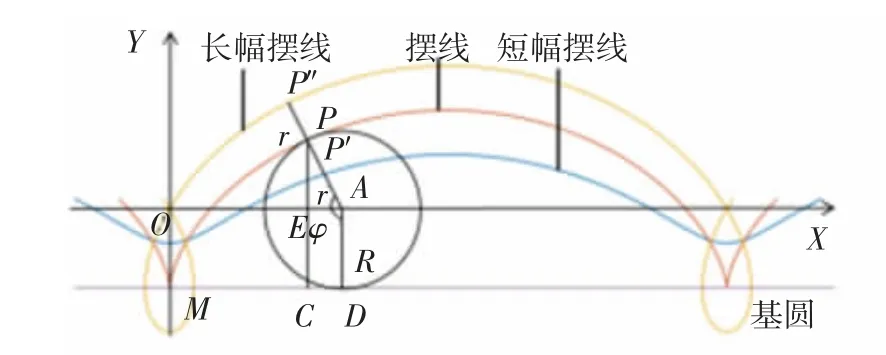
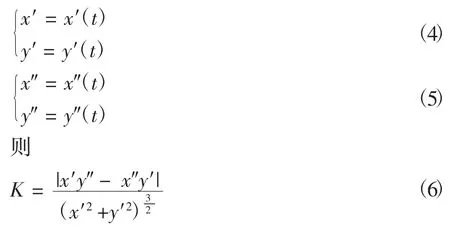
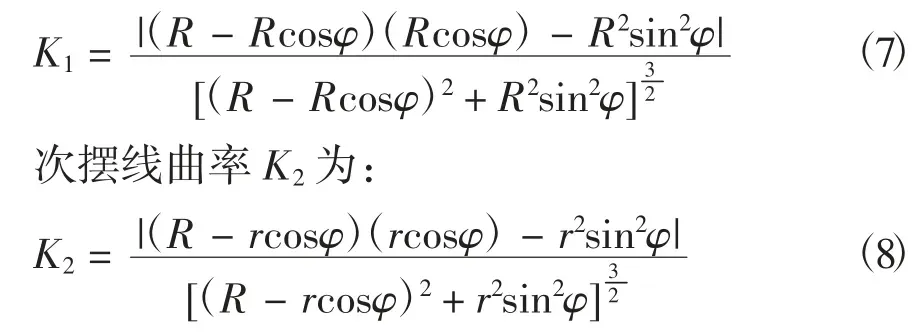
1.2 铣刀切削刃的真实运动轨迹


2 立铣刀侧铣表面数学建模
2.1 立铣刀刀具曲面数学模型

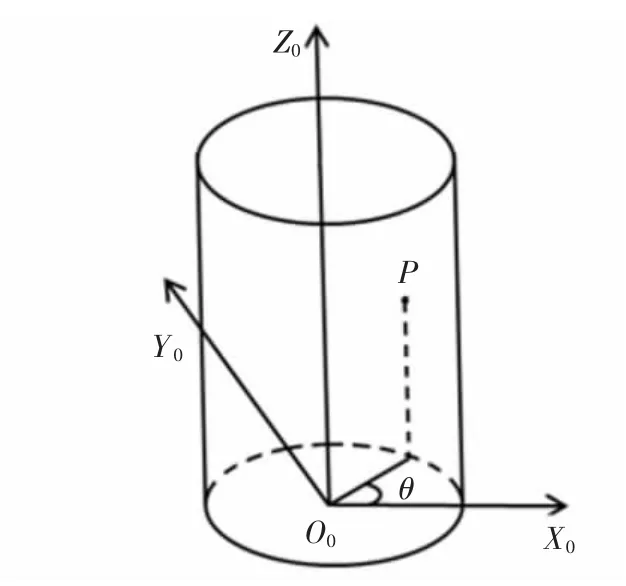
2.2 立铣刀切削刃数学模型



3 立铣刀侧铣工件表面形貌
3.1 扇形残留
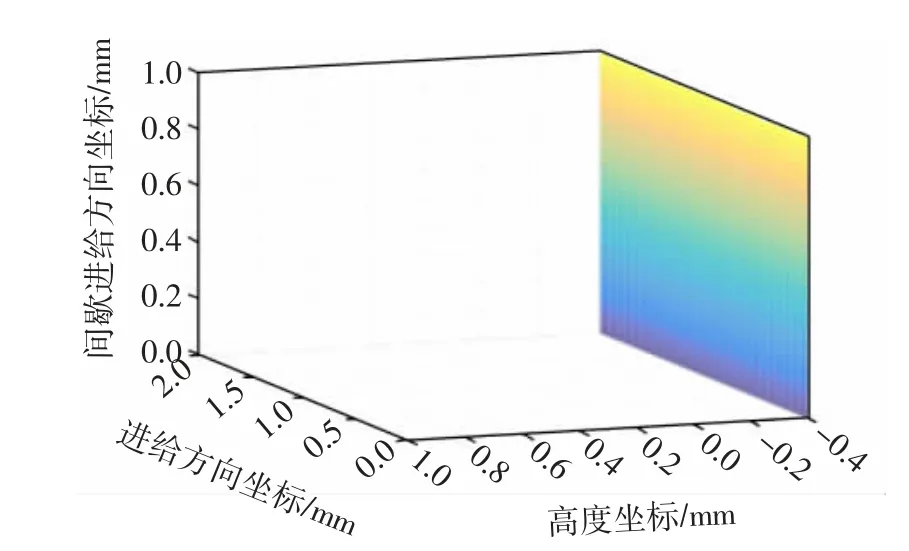
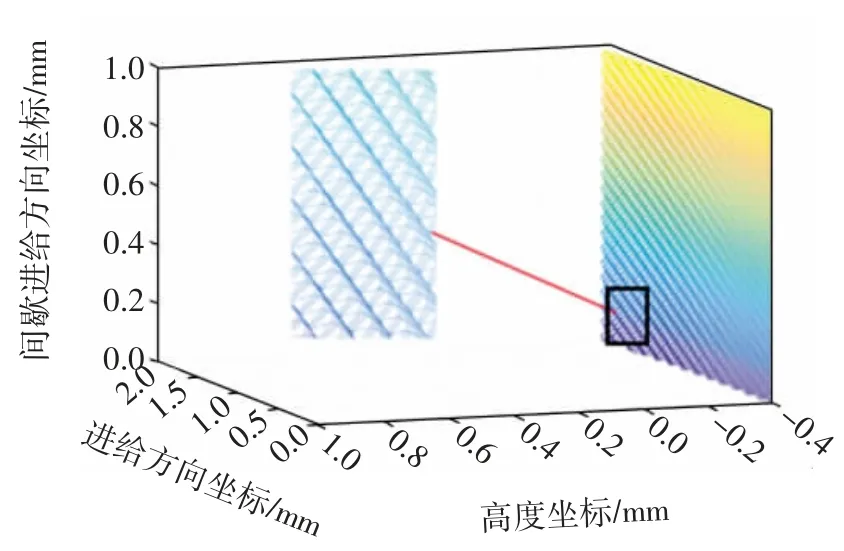


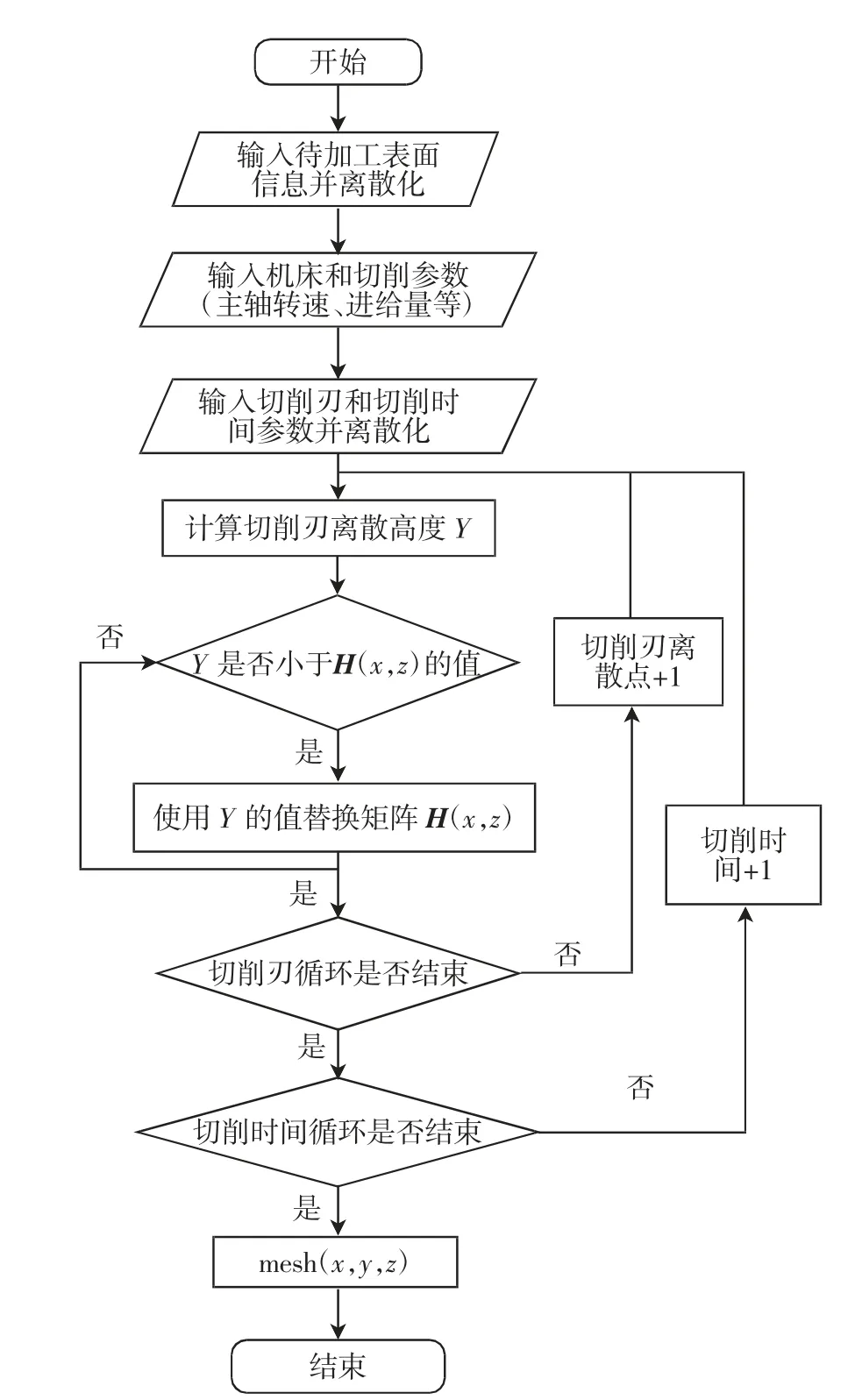
3.2 仿真算法

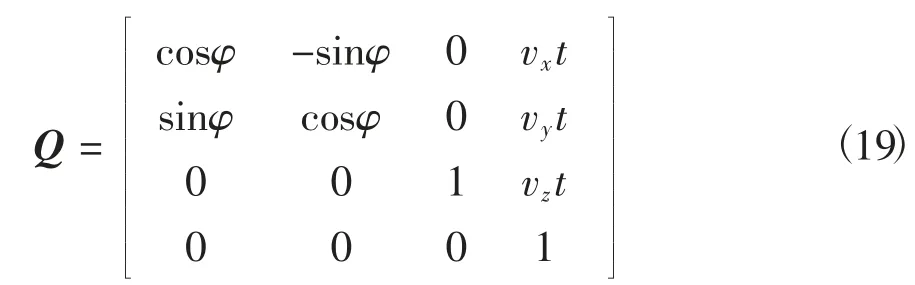
3.3 扇形残留仿真研究




4 结论

