地球表面测向交叉定位算法

赵辰乾，王松波，刘益辰

(中国船舶工业系统工程研究院，北京 100094)

0 引 言

目标定位在战争中具有重要意义，确定目标位置有助于了解敌方的军事部署，进而为武器打击提供引导。电子侦察通过被动接收辐射源目标的电磁信号来确定目标位置，具有作用距离远、隐蔽接收、不易被敌方察觉的优点。无源定位方法主要有测向交叉定位法和时差定位法。测向交叉定位法无需进行精确的时间同步且只需进行信息级的数据协同，但是定位精度较低。时差定位法需要进行精确的时间同步且需要信号和脉冲级的数据协同，但是定位精度较高。本文主要研究测向交叉定位算法。

测向交叉定位方法已经非常成熟，经典算法有几何定位法、最小二乘法[1]、离散概率密度法[2]和最大似然法[3]等，但是这些经典算法都基于二维平面场景，没有考虑地球曲率的影响，在实际应用中，对远距离目标和高纬度目标的定位误差过大。目前，众多学者也提出了许多基于地球表面的交叉定位算法。文献[4]提出了基于椭球模型的定位算法，该算法计算复杂度低且系统误差极小，但是只适用于两站交叉定位场景。文献[5]提出了基于地球椭球参考平面的定位算法，该方法可以部分消除地球曲率的影响，但是需要额外参考点，且对参考点的选取非常敏感，选取不当的参考点时，定位误差很大[6]。除此之外，还可以采用迭代法求解非线性定位方程组，但是该方法具有计算量大、存在迭代不收敛情况、无解析解等问题。针对上述问题，本文提出了基于距离误差最小和地球表面约束的交叉定位算法，算法适用于双站和多站场景，对于远距离目标和高纬度目标的系统定位误差极小，同时具备有解析解、无需迭代等优点。

1 算法原理

本文提出的交叉定位算法基于距离平方和最小准则和地球表面约束，即定位点位于地球表面且距离各侦察站测向面的距离平方和最小。本算法是一种典型的最优化问题，可用拉格朗日乘子法进行求解。

假设共有M(M≥2)个侦察站参与交叉定位，第i个站的经度为Li，纬度为Bi，高度为Hi，测向方位角为φi。

首先，计算各侦察站的地心地固(ECEF)坐标和测向面的法向量，设第i个站的ECEF坐标为(xi,yi,zi)，测向面法向量为fi。

经纬高与ECEF坐标转换公式如下：

(1)

式中：a为地球椭球的半长轴；b为半短轴；e为偏心率。

侦察站测向面法向量的计算公式为：

f=[sinBcosLsinφ-sinLcosφ,

sinBsinLsinφ+cosLcosφ,-cosBsinφ]T

(2)

然后，利用距离误差与地球表面约束方程构造拉格朗日函数，求解定位点位置，此部分是算法的核心。

(3)

定位点的地球表面约束方程为：

(4)

利用式(3)和式(4)构造拉格朗日函数：

(5)

将式(5)表示为矩阵形式：

(6)

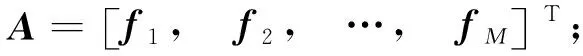
求解拉格朗日函数γ，可得：

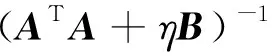
(7)

由于地球长短半轴长度非常接近，因此矩阵B可以近似为单位阵，此时式(7)可以近似为：

(8)

忽略地球偏心率，式(4)可以近似为xTx=a2，将式(8)代入其中计算k值，可得：

(9)

(10)

将式(8)和式(9)代入式(6)可得：

γ=xTATAx-xTATg-gTAx+gTg=

a2λi-2api

(11)

(12)

最后，计算定位点到侦察站的距离，距离较小者为正确定位点，并将其ECEF坐标转换为经纬高，转换公式如下：

(13)

2 仿真验证

本节通过仿真实验验证算法在双站和多站情形下以及有无测向误差情况下的定位误差。

(1) 无测向误差

场景一：双站测向交叉定位

两站经纬度分别是(-1°，30°)和(1°，30°)，定位误差如图1所示。

图1 无测向误差，双站定位误差分布图

场景二：三站测向交叉定位

三站经纬度分别是(-1°，30°)、(1°，30°)和(0°，31.7°)，定位误差如图2所示。

(2) 有测向误差，测向误差的标准差为1°，误差服从零均值正态分布

场景三：双站测向交叉定位

两站经纬度分别是(-1°，30°)和(1°，30°)，定位误差如图3所示。

场景四：三站测向交叉定位

三站经纬度分别是(-1°，30°)、(1°，30°)和(0°，31.7°)，定位误差如图4所示。

结论：算法适用于双站和多站定位场景。当测向误差为0时，算法对于1 000 km内目标的系统定位误差在米级,远小于测向误差造成的定位误差，基本可以忽略。

3 结束语

通过算法原理和仿真结果可知，本算法具有以下三方面优点：

从算法实现角度考虑，本算法的主要计算量是三阶实对称矩阵的特征分解，计算复杂度低，无需迭代，有解析解。

从算法误差角度考虑，本算法对于1 000 km以内目标的系统定位误差在米级，远小于测向误差造成的定位误差，满足实际需要。

从算法适用场景考虑，本算法适用于双站和多站交叉定位场景。

综上所述，本算法可以很好地应用于实际工程中。