苏州市高速公路安全统计建模

张琪 王雪松 丰明洁 裴莹莹 邓毅萍

摘 要：高速公路作为连接长三角地区的重要通道，承载了大量的交通需求。通过安全建模分析，识别长三角都市圈通勤时段高速公路交通事故特征及交通安全主要影响因素，提高其运行安全和效率，有利于推进长三角城市群交通一体化建设。本文采集苏州市10条高速公路双向的交通事故数据、道路几何数据和交通运行数据，考虑空间相关性，基于微观路段单元，建立了贝叶斯负二项条件自回归模型。结果表明，道路几何特征、交通运行特征对高速公路安全均存在显著影响。

关键词：长三角都市圈；高速公路；贝叶斯负二项条件自回归模型；影响因素

基金项目：道路交通安全“十四五”规划（2020SJD06），道路安全现状分析与对策研究专题

Safety modeling for freeway in Suzhou

ZHANG Qi1，WANG Xuesong1，FENG Mingjie1，PEI Yingying1，DENG Yiping2（1.Key Laboratory of Road and Traffic Engineering of the Ministry of Education， Tongji University， Shanghai 201804， China；2.Traffic Management Research Institute of the Ministry of Public Security，Wuxi 214151，China）

Abstract： As an important passage connecting the Yangtze River Delta， freeways carry a large amount of traffic demand. It is necessary to conduct corresponding safety analysis， in order to identify the characteristics and impact factors of freeway crashes during commuting periods in the Yangtze River Delta metropolitan area. Geometric features， traffic operational factors were gathered from the 10 freeways in Suzhou， China. Considering spatial correlations， a set of Bayesian Negative Binomial Conditional Autoregressive（NB-CAR）model was selected as prediction model based on micro-level analysis units. Results indicate that geometric features and traffic operational factors are substantially associated with crash frequencies.

Keywords： Yangtze River Delta metropolitan areas；freeway；Bayesian Negative Binomial Conditional Autoregressive model；effect factors

截至2019年，長三角地区高速公路总里程为1.49万公里，高速公路覆盖率显著高于全国平均水平，其中苏州市高速公路里程达608公里[1]。高速公路作为连接长三角都市圈的重要通道，提供了中大量、长距离的快速交通服务，承担着长三角区域大量的过境交通。由于高速公路交通流量大、行车速度高的特点，一旦发生事故将造成极大的生命财产损失和交通运行影响。识别高速公路通勤时段的交通事故特征，保证交通安全和通畅，对苏州市乃至整个长三角区域尤为重要。因此研究高速公路事故影响因素有助于为其运行、管理提出有效的改善措施。

交通事故数据具有离散性、非负性、随机性、非正态分布等特点，传统的线性回归模型无法对事故数据进行很好的拟合。因而建立了广义线性回归模型来进行事故预测，其中泊松模型和负二项模型被广泛用于拟合事故的发生[2]。然而广义线性模型均假设研究的样本相互独立，并未考虑事故数据的层次结构性，如研究单元的空间相关性，可能会造成错误的估计。由于高速公路沿线路段在几何设计、交通运行特征等方面存在未观察到的相似之处，为解决由此导致的空间相关性，条件自回归模型被广泛应用于高速公路事故建模[3-5]。该模型克服了广义估计方程理论的局限，可灵活设置组内研究单元间的关联系数。

本研究基于苏州市10条高速公路的微观路段单元的数据，考虑空间相关性，建立条件自回归负二项模型。针对高速公路高峰通勤时段，研究其道路几何特征和交通运行特征与事故发生频率之间的关系。

1数据准备

1.1高速公路选取与路段划分

本文以苏州市10条高速公路为分析对象，将其划分为微观分析单元：主线路段每1公里划分为一个微观单元；出入口路段考虑到出入口匝道对交通运行的影响，以匝道位置对路段进行划分。最终，10条高速公路共划分为1013个微观路段研究单元。

1.2数据采集

交通事故数据来源于苏州市2019年全年高速公路交通事故记录。针对划分的微观研究单元，采集车道数、匝道类型、路段长度等微观路段的道路几何变量，采集到的匝道类型如图 1所示。流量数据来源于高速门架信息和交通流量表，统计高峰小时流量。速度数据来源于高德平台，采集10条高速公路所有路段的速度数据，并计算高峰小时的平均速度。道路几何设计变量和交通运行变量的统计信息如表 1、表 2所示。

2安全统计模型与估计方法

2.1贝叶斯负二项条件自回归模型

贝叶斯方法可以结合先验分布，利用原有模型为现有数据建模提供先验依据，从而得出更好的拟合结果。先验分布可以由经验得出，也可以是无信息的先验分布。该方法可以有效避免由于数据偏差过大造成结果的不可靠。理论框架如下：

2.2模型结果

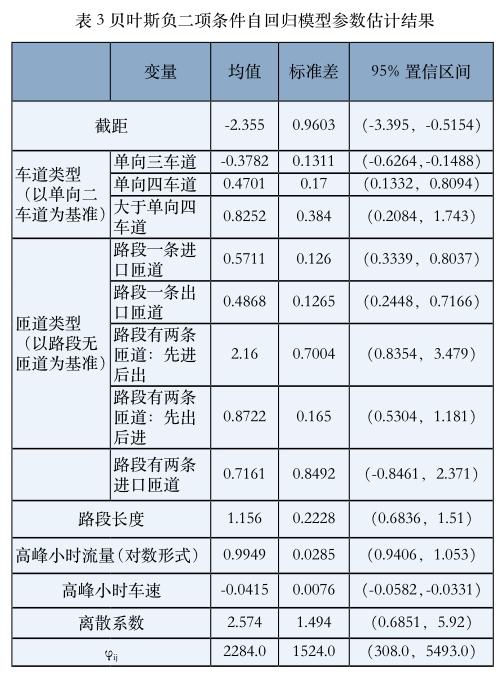
贝叶斯估计通过马尔科夫链算法来完成。本文利用WinBUGS软件的吉布斯取样法（Gibbls Sampling）模拟马尔科夫链，从而完成对贝叶斯模型的标定。假设模型中的随机效应项的方差和负二项分布的离散系数均服从逆伽马分布，设定马尔科夫链进行20000次迭代，并舍弃前4000次不稳定迭代。参数估计结果如表3所示。

95%置信区间不包含零说明对应的估计参数是显著的。根据事故预测模型的参数估计结果，可以看出道路几何变量和交通运行变量均为交通事故的显著影响因素。

3安全影响因素分析

3.1道路几何特征

根据表3，车道属性部分，单向三车道的系数为负值且在95%置信水平下显著，表明单向三车道的事故频率显著低于单向二车道。单向四车道及大于单向四车道的模型系数均为正值且在95%置信水平下顯著，表明车道数到达一定程度时，高速公路交通事故随着车道数的增加而增加且显著相关。Kononov等[6]利用神经网络模型研究车道数与交通安全之间的相关关系，也得到类似的结论。这可能与随着车道增加而导致的变道行为增加有关，早晚通勤高峰期间交通流量较大，驾驶人会倾向频繁变道以保证自己运行顺畅，而在高速公路上，以较快的速度进行变道，容易导致追尾事故和侧碰事故。

匝道类型部分，路段有一条进口匝道、一条出口匝道、先进后出匝道和先出后进匝道的模型系数显著为正。说明相比无匝道的路段，有一条进口匝道、出口匝道、先进后出和先出后进匝道会增加路段的事故风险。交通流频繁分流和汇入，会对主线交通造成干扰，因此路段存在进口匝道或出口匝道均会增加路段发生事故的可能性。路段有两条进口匝道的模型系数不显著，可能与样本量过小有关。

路段长度部分，模型结果显示，路段长度变量显著且符号为正，这说明高速公路交通事故随微观路段长度增加而增加。高速公路交通流作为连续流，以极高的车速运行，且驾驶环境较为单一，驾驶人面临突发情况可能会反应不及，容易造成事故。

3.2交通运行特征

路段高峰小时流量的对数与事故频率呈显著正相关关系，即随着高速公路路段流量的增加，事故频率也随之增加。当交通流量增多时，车辆之间的互相干扰会显著增加，严重影响交通运行安全和效率。

路段高峰小时平均速度与交通事故呈显著的负相关关系，即高速公路路段事故随着速度的增加而降低。较高的运行速度，说明高速公路路段运行情况畅通，而较低的运行速度，则说明路段交通运行情况不佳，有可能发生交通拥堵或事故，该情况易发生追尾和侧碰等事故。

4总结

本文以苏州10条高速公路为研究对象，建立贝叶斯负二项条件自回归模型，发现路段长度、高峰小时流量、高峰小时速度、车道数和匝道类型均会对高速公路路段事故数产生显著影响。该结果揭示了以苏州市为例的高峰通勤时段道路几何特征与交通运行特征对高速公路交通事故的影响，为苏州市高速公路交通安全管理工作及未来长三角都市圈交通规划的实施提供一些借鉴。

参考文献

[1] 苏州市统计局.苏州市统计年鉴（2020）[M]. 北京：中国统计出版社，2020.

[2] DANIEL J R， MAINA E. Relating Safety and Capacity on Urban Freeways. 6th International Symposium on Freeway Capacity and Quality of Service， Stockholm， Sweden. 2011.

[3] XIE K， WANG X， OZBAY K， YANG H. Crash frequency modeling for signalized intersections in a high-density urban road network [J]. Analytic Methods in Accident Research. 2014， 2： 39-51.

[4] MA X， CHEN F. Multivariate space-time modeling of crash frequencies by injury severity levels[J]. Analytic Methods in Accident Research. 2017， 15 ： 29-40.

[5] WANG X， FENG M. Freeway single and multivehicle crash safety analysis： Influencing factors and hotspots [J]. Accident Analysis & Prevention. 2019， 132.

[6] KONONOV J， BAILEY B A， ALLERY B K. Exploratory Analysis of Relationship between the Number of Lanes and Safety on Urban Freeways[J]. Journal of the Transportation Research Record， Washington D.C： Transportation Research Board of the National Academies. 2008.