正弦表面结构的薄膜失稳形貌有限元分析和实验验证

杨玺琳，刘海东，贾 飞，吴良科，古 斌

(1.西南科技大学 制造科学与工程学院，四川 绵阳 621010；2.哈尔滨工业大学 航天科学与力学系，哈尔滨 150001；3.重庆大学 航空航天学院，重庆 400044)

表面褶皱现象在自然界中广泛存在，特殊的表面微形貌可以赋予材料不同的功能[1-3]，因此如何构筑复杂的表面形貌具有十分重要的理论与实际应用价值。近年来，研究人员通过表面失稳、化学刻蚀、光诱导的高分子交联技术、纳米压印、等离子体处理等手段构筑材料表面微结构[4-8]。其中，表面失稳以其形貌和尺度易于调控、构筑方法简易、成本低廉和大量潜在应用等优点受到学者青睐[9-11]。

(1)

(2)

式中，μf和μs分别为薄膜和基底的剪切模量，h为薄膜厚度，薄膜和基底的泊松比均取为0.5。在此基础上，Cai等[13]探讨了微小曲率对平面薄膜临界失稳载荷和波长的影响，并给出了修正后的值为

(3)

(4)

式中Ω为与曲率相关的量，可表示为：

(5)

式中R为薄膜的初始曲率半径。

1 有限元分析

1.1 有限元模型

图1 具有正弦表面结构的薄膜基底系统示意图Fig. 1 Schematic diagram of a film-soft substrate system with a sinusoidal structure

模糊综合评判法中的权重向量W=(w1,w2,w3,w4)反映了对各信任因素的关注程度,w1、w2、w3、w4分别为4个信任因素的权重,需满足w1+w2+w3+w4=1。本文采用常用的常值权重,且令w1=w2=w3=w4=1/4。

1.2 数值结果和讨论

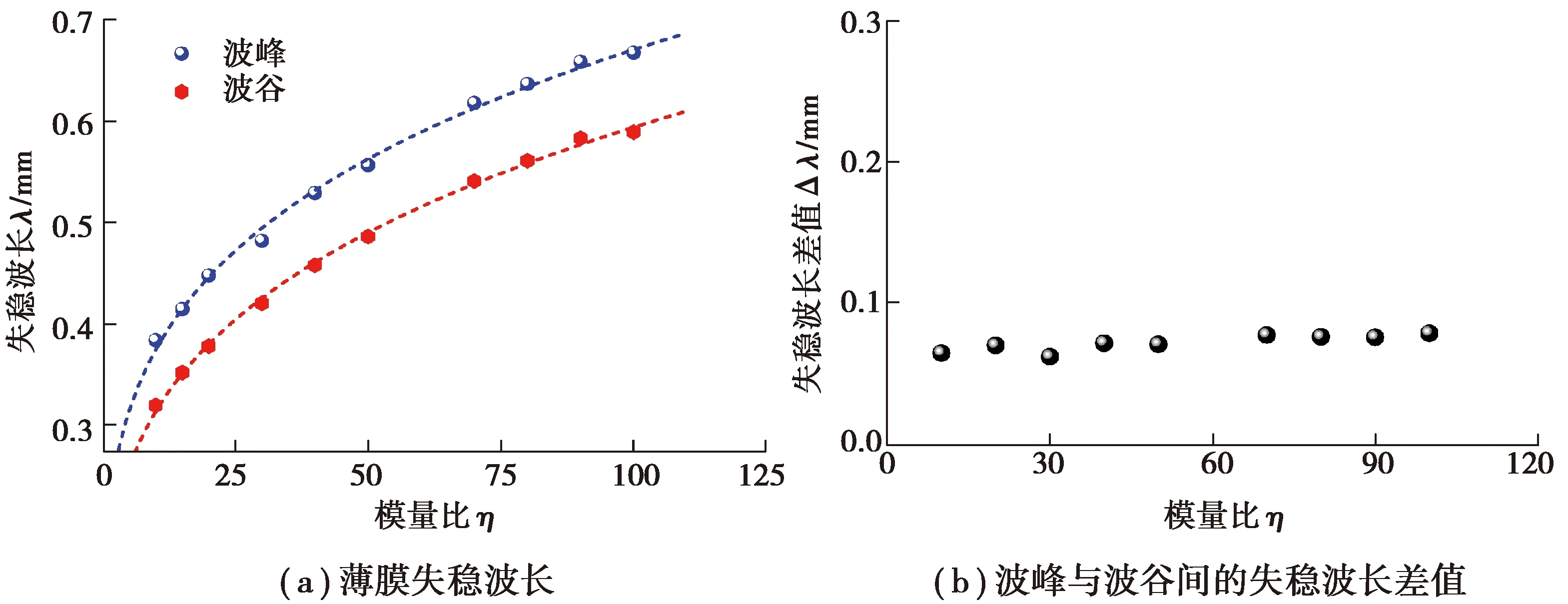
图2 当A=0.25 mm，h=0.05 mm，ξ=0.2时，正弦薄膜失稳形貌随薄膜基底模量比的变化Fig. 2 When A=0.25 mm, h=0.05 mm, ξ=0.2, the instability of the sinusoidal film changes with the film-substrate modulus ratio

1.2.2 预拉伸变形量的影响

选定变量A=0.25 mm，h=0.05 mm，η=80，预拉伸变形量在0.15≤ξ≤0.35范围内取值，正弦表面结构波峰和波谷处的失稳波长及两位置间失稳波长差值的变化分别如图3(a)和图3(b)所示。图中结果表明预拉伸变形量的增加会导致波峰和波谷处失稳波长的减小，而两位置间的失稳波长差值则轻微增大。波峰和波谷处失稳波长的变化近似符合线性规律，可分别用线性拟合函数λ=-0.90ξ+0.81(波峰处)和λ=-1.08ξ+0.77(波谷处)表示，(如图3(a)中虚线所示)。

图3 当A=0.25 mm，h=0.05 mm，η=80时，正弦薄膜失稳形貌随预拉伸变形量的变化Fig. 3 When A=0.25 mm, h=0.05 mm, η=80, the instability of the sinusoidal film changes with the pre-stretch deformation

1.2.3 薄膜厚度的影响

为研究薄膜厚度对失稳波长的影响，取A=0.25 mm，η=80，ξ=0.2以及0.05 mm≤h≤0.1 mm。相应的有限元模拟结果见图4(a)和图4(b)。从图4(a)可以看出，波峰和波谷处的失稳波长均随着薄膜厚度的增加而增加，且变化规律可近似用线性拟合函数表示，即λ=12.87h(波峰处)和λ=11.60h(波谷处)。此外，波峰与波谷间的失稳波长差值也随着薄膜厚度的增加而增大，但变化不明显，如图4(b)所示。

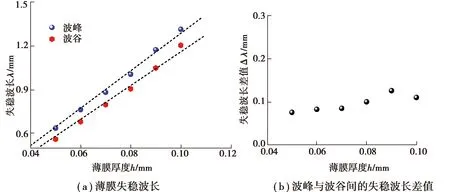
图4 当A=0.25 mm，η=80，ξ=0.2时，正弦薄膜失稳形貌随薄膜厚度的变化Fig. 4 When A=0.25 mm, η=80, ξ=0.2, the instability of the sinusoidal film changes with the thickness of the film

1.2.4 正弦表面结构幅值的影响

当h=0.25 mm，η=80，ξ=0.2时，正弦表面结构波峰和波谷处的失稳波长随正弦表面结构幅值的变化如图5(a)所示，其中正弦表面结构幅值的变化范围为0≤A≤1 mm。图中可以看出，随着正弦表面结构幅值的增大，波峰处的失稳波长呈整体增大的趋势，而波谷处的失稳波长呈整体减小的趋势。两者都不随正弦表面结构幅值的改变而单调变化。两位置间的失稳波长差值随正弦表面结构幅值的改变发生显著变化，且表现出随正弦表面结构幅值增加而近似线性增大的规律。该规律可用拟合函数Δλ=0.36A表示，见图5(b)。另外注意到，当正弦表面结构幅值大于一定值时，如A≥0.8 mm，在波峰处将不发生表面失稳，相应的失稳波长差值也未给出。

图5 当h=0.25 mm，η=80，ξ=0.2时，正弦薄膜失稳形貌随正弦表面结构幅值的变化Fig. 5 When h=0.25 mm, η=80, ξ=0.2, the instability of the sinusoidal film changes with the amplitude of the sinusoidal surface structure

1.3 膜基系统表面失稳波长的经验公式

λ=kh(ξ+c)ηb。

(6)

图6 当h=0.05 mm，ξ=0.2时，平面膜基系统的失稳形貌Fig. 6 When h=0.05 mm, ξ=0.2, the instability morphology of the planar film-based system

图7 当ξ=0.2, η=80时，平面膜基系统的失稳波长随薄膜厚度的变化Fig. 7 Variation of the instability wavelength of film-substrate system of flat surface with the film thickness when ξ=0.2, η=80

2 表面失稳形貌的调控以及实验验证

2.1 表面失稳形貌调控的有限元模拟

前述有限元分析表明，利用不同的参数组合可以对薄膜表面失稳形貌进行调控。此外，通过赋予波峰和波谷区域薄膜不同的性质，如剪切模量和厚度，也能改变薄膜的表面失稳形貌。图8显示了当λ0=10 mm，A=0.5 mm，h=0.05 mm，ξ=0.2时，波峰和波谷区域薄膜取不同剪切模量引起的表面失稳形貌。在本文中考虑了4种情况：1)μb∶μt∶μs=50 ∶500 ∶1；2)μb∶μt∶μs=1 ∶20 ∶1；3)μb∶μt∶μs=200 ∶20 ∶1；4)μb∶μt∶μs=20 ∶1 ∶1。μb和μt分别为波谷和波峰处薄膜的剪切模量，基底的剪切模量保持不变且μs=1.0 MPa[15]。由图8(a)和(c)可知，当μb≠μt>μs时，正弦薄膜表面出现类似双波长正余弦条纹的形貌[15]。而且某区域剪切模量越大，该区域产生的失稳波长越长，这与图2中均匀薄膜(μb=μt>μs)的结果一致。但由于波峰与波谷处薄膜的剪切模量不同，两位置间的失稳波长差值也有很大的差异。这与均匀薄膜时薄膜剪切模量几乎不影响失稳波长差值不同。因此，通过控制薄膜不同区域的剪切模量，可实现对局部失稳波长和区域间失稳波长差值的调控。特别是当μt>μb=μs或μb>μt=μs时，仅有波峰或波谷区域产生表面失稳，如图8(b)和(d)所示。

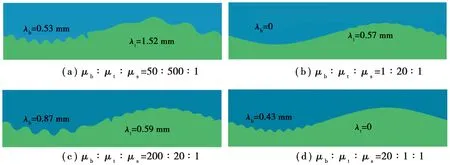
图8 波峰、波谷与基底不同剪切模量的失稳模态Fig. 8 Instability modes of different Young’s modulus of the crest, trough and base

与调节剪切模量类似，改变薄膜不同区域处的厚度也能改变薄膜的表面失稳形貌，实现对失稳波长和失稳波长差值的调控，如图9所示。此时λ0=10 mm，A=0.5 mm，η=50，ξ=0.2，考虑4种薄膜厚度组合：(a)hb=0.05 mm，ht=0，(b)hb=0.05 mm，ht=0.02 mm，(c)hb=0，ht=0.05 mm，(d)hb=0.02 mm，ht=0.05 mm。hb和ht分别为表面波谷和波峰区域的薄膜厚度。当hb≠ht时，正弦薄膜表面同样出现类似双波长正余弦条纹的形貌，如图9(b)和(d)所示。而且表面薄膜越厚的区域，失稳波长越长，波峰与波谷间的失稳波长差值也与不同区域的薄膜厚度相关。特别当表面薄膜厚度为0时，该区域将不会发生表面失稳，如图9(a)和(c)所示。

图9 波峰与波谷位置处薄膜厚度不同时的失稳模态Fig. 9 Instability modes when the film thickness at the peak and trough is different

2.2 表面失稳形貌调控的实验验证

实验以道康宁公司生产的硅橡胶-PDMS184为原材料。主要仪器包括行星搅拌机(型号AR-100，日本THINKY公司)、干燥箱(型号DHG-9075A，上海一恒科学仪器有限公司)、UV表面照射装置(型号BZZ250G-T，汇沃科技有限公司)和扫描电子显微镜(型号7610F，日本电子株式会社)等。

图10 具有正弦结构表面的PDMS样品 Fig. 10 PDMS sample with sinusoidal surface

图11 正弦结构波峰与波谷位置处失稳形貌差异化的制备方法Fig. 11 Preparation method of differential instability at the peak and trough positions of a sinusoidal structure

利用场发射扫描电镜观测样品表面失稳形貌并测量波峰和波谷处的失稳波长，不同辐照时长的样品表面失稳形貌如图12所示。其中样品1波谷处失稳波长为29.813 μm，波峰处失稳波长为124.219 μm，如图12(a)和(b)所示。样品2波谷处失稳波长为97.031 μm，波峰处失稳波长为37.688 μm，如图12(c)和(d)所示。由于硬化处理时间越长，薄膜的剪切模量和厚度越高。样品1对应图8中算例(a)和图9中算例(d)，样品2对应图8中算例(c)和图9中算例(b)。比较可知，实验结果与有限元模拟结果定性吻合。即薄膜剪切模量和厚度越高(硬化处理时间越长)，失稳波长越长，而且改变不同区域的辐照时间，可以有效调控波峰与波谷区域失稳波长的差值。因此，实验结果验证了所提出的有限元模型和结果的正确性，同时该实验工艺对于实际构筑特殊表面微形貌具有一定的参考价值。另外必须指出：由于实验中薄膜的弹性模量和厚度同时受辐照时间影响，且难以精确测量，无法为数值模拟提供准确的参数。现阶段实验结果仅能定性地验证数值模拟结果，实现定量验证还需进一步的系统研究。

图12 不同辐照时长正弦样品波峰与波谷位置的失稳形貌SEM图像Fig. 12 SEM images of the instability of the peak and trough positions of long sinusoidal samples at different irradiation times

3 结 论

3)根据有限元结果提出了利用非均匀薄膜调控表面失稳形貌的方案，并进行了实验验证，实验结果与数值结果定性吻合。同时，实验工艺提供了一种可用于构筑特殊表面微形貌的简便方法。

研究成果有助于理解自然界中某些特殊表面形貌的形成机理，在物理、仿生以及超疏水材料等领域具有广泛的应用前景。