Hamel 框架下几何精确梁的离散动量守恒律1)

高 山 史东华,2) 郭永新

*(北京理工大学数学与统计学院,北京 100081)

†(辽宁大学物理学院,沈阳 110036)

引言

柔性梁的动力学广泛存在于力学系统当中,其研究发展不断与固体力学、流体力学、非线性动力学、生物力学等其他学科进行交叉[1-4].几何精确梁模型作为容许大范围运动、大变形的柔性梁的理想模型,自提出后在分析、数值、应用等方向吸引了大量关注[5-11].在柔性机器人的运动控制[12-13]、DNA动力学的研究[14]中有广泛的应用.

在几何精确梁的数值算法方面,传统数值格式直接离散动力学方程,可以实现连续系统的计算仿真,但是很难保持系统内在的对称性、守恒性等物理特性,如能量、动量等.Marsden 等[15]提出的变分积分子是一种从Lagrange 函数出发,通过离散变分原理直接得到保结构数值格式的方法.Demoures 等[16]提出的几何精确梁的李群积分子和李代数积分子可以自然保持能量动量,但没有充分利用系统对称性,对于几何精确梁等对称性很强的系统离散格式复杂程度很高.在此基础上,Ball 等[17]对有限维系统提出了Hamel 变分积分子,主要适用于带对称性的约束力学系统,特别是带对称性的非完整约束力学系统.Shi 等[18-20]进一步应用无穷维几何中的活动标架法结合变分原理,得到约束无穷维力学系统和经典场论中刻画运动的标准型—–Hamel 形式,进而得到能用于经典场论动力学计算的保结构格式—–Hamel 场变分积分子.Hamel 场变分积分子可以无需额外的Lagrange 乘子来求解无穷维约束力学系统,特别是非完整力学系统.其是一种分布式算法,每一次计算只需利用待计算点周围的信息,具有计算效率高的特点.王亮等[7]将Hamel 场变分积分子应用于几何精确梁,并通过数值算法验证了Hamel 场变分积分子能长时间保结构的特征.

保结构性质对非线性力学系统的长时间定性行为的了解和定量分析是非常必要的.这里结构包括辛结构、酉结构、体积结构、接触结构、泊松结构等几何结构,也包括能量、动量、系统特征值等首次积分结构[21].在天体力学[22-23]、量子力学[24]、电磁学[25]等学科中许多模型数值算法的构造中,尽可能多地保持原系统的内在对称性、守恒性等物理特征的算法往往表现出很强的数值预测能力和跟踪能力[21].例如,电磁学中受到广泛应用的Yee 格式已被证明保持多辛结构和动量映射[26].在保结构算法的理论研究上,钟万勰等[27]建立了一套Hamilton 动力系统的辛几何方法,张素英等[28]在此基础上,对Poisson 流形上的广义Hamilton 系统的数值算法进行了研究,提出了广义Hamilton 系统显式的保持真解典则性的数值方法.刘世兴等[29]研究了特定的非完整系统的辛算法,并将其与Runge-Kutta 法进行对比,说明了辛算法具有高的精确度.满淑敏等[30]提出了一类求解非完整系统的保结构算法,并证明了其对称性,说明了其收敛性和长时间保结构的特性.

对Hamel 变分积分子的现有研究结果在数值上充分表现出了其对非线性系统,包括有限维系统、无穷维系统、完整系统与非完整系统,长时间动力学行为的良好预测[7,17,20].本文以几何精确梁为例,利用离散Noether 定理,研究了Hamel 场变分积分子的保动量性质,以期为进一步研究其保结构性质提供参考依据.

1 几何精确梁的动力学模型

考虑一个在空间中运动的质量均匀的弹性梁.设{E1,E2,E3} 为物质标架的一组基,初始时刻梁沿E2轴水平自然放置(无弹性形变),一端位于原点(见图1).设梁长为l,密度为ρ,截面面积为A的正方形.

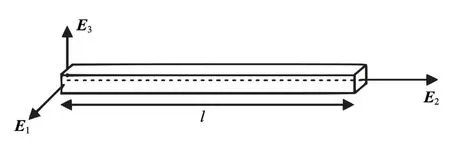
图1 几何精确梁初始位形Fig.1 Initial configuration of a geometrically exact beam

在几何精确梁的模型中,梁的截面做刚体运动,其位形可由

描述,其中φ:R×[0,l] → R3为中线位置函数,Λ:R×[0,l] →S O(3) 为截面旋转矩阵.引入对流速度

和对流应变

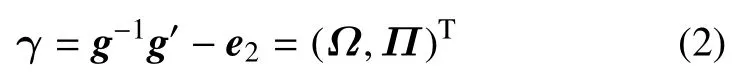
其中顶标·和上标′分别表示对时间变量t和空间变量s求导,e2为E2方向的单位向量.此处利用了李代数se(3) 与R6的等同.对流速度ζ包含了截面运动的角速度ω和平移速度π的信息,对流应变包含了弹性拉伸、弯曲和剪切信息.从而,几何精确梁的Lagrange 密度可写作

其中〈·,·〉为se*(3)与se(3)配对,K,P 分别为常对角阵.从而作用泛函为

令η=g-1δg为独立变分,易知η与ζ,γ满足如下变分公式[20]

其中[·,·]为se(3)上的李括号.

根据变分公式和Hamilton 原理,计算得到自由几何精确梁的动力学方程

和自由边界条件

其中[·,·]*为se(3)李括号[·,·]的对偶括号.同时,由式(1)和式(2)可知,ζ和γ满足相容性条件

相容性条件描述了对流速度和对流应变生成的分布的可积性.在场论框架下,位形g是以时空为底流形,纤维为的主丛S E(3)的截面,相容性条件在几何上可解释为主丛的局部平坦性条件.对一般纤维丛情况下的相容性条件的讨论参见文献[19].对于给定初始条件和边界条件的几何精确梁,其运动由动力学方程(3)和相容性条件(5)共同确定,将式(3)和式(5) 构成的方程组称为几何精确梁的Hamel 场方程组[18-19].

2 几何精确梁Hamel 场变分积分子

通过离散Hamilton 原理得到Hamel 场变分积分子.设离散梁的空间节点数为K,空间步长为Δh,时间步数为N,时间步长为Δt.梁的位形由序列n=0,1,2,···,N-1,j=1,2,···,K描述,表示在n时刻第j个截面的位形.分别定义离散对流速度和离散对流应变如下

由于指数映射exp :se(3) →S E(3)是局部微分同胚,在exp:se(3)→S E(3)与相距较近,即在exp 的值域中时,上式唯一确定了离散对流速度,离散对流应变的情形类似.从而,离散Lagrange 密度为相应的作用和为

注:上式中第一项的求和范围应为n=0,1,2,···,N-1,j=1,2,···,K,第二项的求和范围应为n=1,2,···,N-1,j=0,1,2,···,K.为了后续计算表达式的简洁,本文将上式求和范围统一写为n=0,1,2,···,N-1,j=0,1,2,···,K,将指标溢出的变量统一记为0.

及离散相容性条件

3 Hamel 场变分积分子保动量性质

本节首先证明自由的(不受外力、外力矩) 的几何精确梁系统具有动量守恒性质,随后通过离散Noether 定理[31]证明Hamel 场变分积分子可以保持精确离散动量.

根据经典力学理论,一个不受外力(矩) 的完整力学系统总动量保持不变,故自由运动的几何精确梁系统具有动量守恒性质.动量守恒往往是在空间坐标下进行验证的,由于Hamel 场变分积分子是在活动标架下给出的,为建立其离散动量守恒,用活动标架表述的梁的动量.

根据Noether 定理,令φ:[a,b]×[0,l]×(-ϵ0,ϵ0)→R,ϵ0＞0 为任意一个以时空和变分变量为自变量的C1光滑的函数,并且满足φ(a,s,ϵ)=φ(b,s,ϵ)=φ(t,0,ϵ)=φ(t,l,ϵ)=φ(t,s,0)=0,∀t∈[a,b],∀s∈[0,l].取定李代数中任意一个元素ξ∈se(3),构造变分曲线

其中g(t,s)为Hamel 场方程的任意一个精确解.下文中均用表示变量依赖于变分参数ϵ.于是的偏导数和无穷小变分δg可分别写作

从而,变分曲线对应的对流速度、对流应变和体坐标系下的变分分别为

将变分曲线代入作用泛函并对其变分,得到

将式(3)代入,得到

其中Ad*表示Ad 算子的伴随算子.由于δφ和ξ的任意性可知

此式为场论框架下的动量律.进一步,对式(11) 在[0,l]上积分,利用空间边界条件(4)可以得到即系统总动量守恒.将此表达式改写到空间坐标系中,即可得到角动量守恒和平动动量守恒的经典表达式.下面,在上述连续情形动量守恒证明的基础上,利用离散Noether 定理进一步证明Hamel 变分积分子也可以自然保持系统离散动量.定义变分序列

体坐标下的变分为

根据式(13)和式(14)和BCH 公式[32]可知

其中算子I:se(3)→se(3)*为

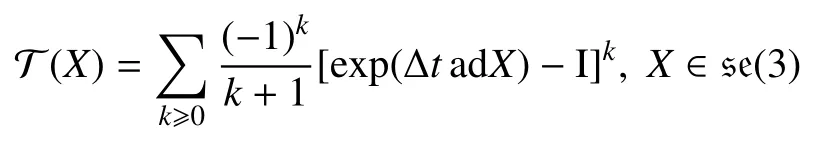
同理可得

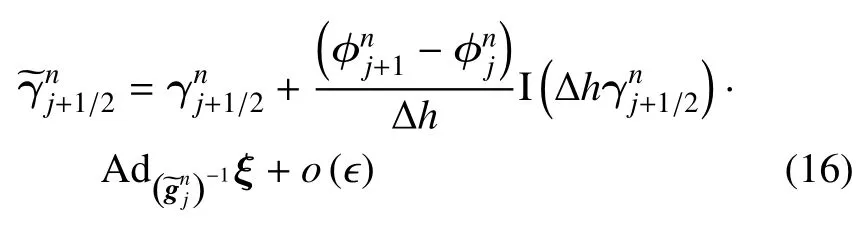
根据离散Noether 定理,将变分序列代入离散Lagrange 密度并对其作用和变分,得到

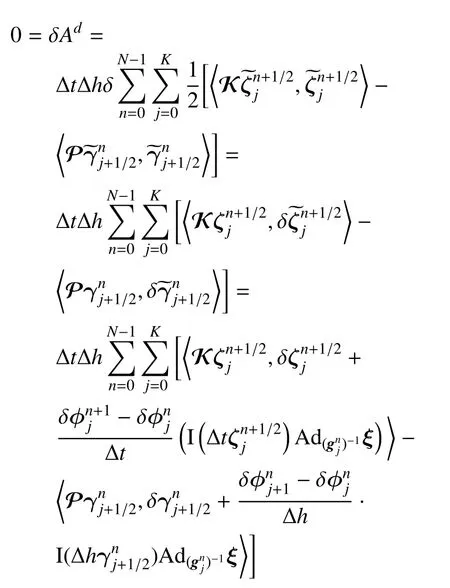
其中最后一个等式利用了变分的定义,可知小量o(ϵ)的变分为零.将离散Hamel 方程代入上式可得

对任意给定的ξ,由于的任意性可知

上式为式(11)的离散对应形式.

上式对j在1,2,···,K上求和并用离散边界条件(9)可得

其中I*为I 的伴随算子.

综上,可以得到如下定理定理3.1.

几何精确梁的Hamel 场变分积分子(8) 和(10)在边界条件(9)下满足如下定义的离散动量守恒

Jd表达式中级数的存在技术上是李代数se(3)非交换性在BCH 公式中的反映,而根本上由于在Hamel 框架下,离散对流速度处于位形与之间,故位形和离散对流速度值无法完全匹配,需离散动量表达式中出现级数来弥补.这种不匹配对于Hamel 场变分积分子的构造是必要的,可以使所得变分积分子具有更高精度[20].值得注意的是,上式中的离散动量可以展开为

这里的首项可作为连续动量(11) 的直接离散,从而Hamel 变分积分子在O(Δt) 误差范围内可以保持此离散动量的首项[7].

4 算例

下面通过两个例子分别从分析和数值角度验证上述结论.

例一考虑一个沿E3方向以v0初速度做匀速直线运动的几何精确梁,不妨设梁长l=1,梁的质量和转动惯量均为1,那么系统总动量非零分量为Jlin3=v0.

在Hamel 框架下,梁的位形可写作

其中y,z分别为截面中线在E2,E3方向的坐标.从而对流速度有表达式

在se(3) 与R6的等同下,ζ=(0,0,0,0,0,)T.令a=(0,0,0,0,0,1)T,由式(12)可得系统在E3方向上的动量为

考虑系统的离散动量,由于在此场景下非平凡的对称群为沿E3轴做平移运动的加法群,指数映射exp退化为线性映射,于是可得

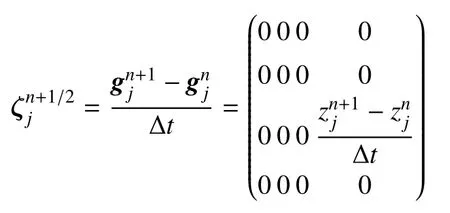
E3方向上离散动量表达式为

这与空间坐标系下的经典动量表达一致.

例二考虑初始位形如图1 所示的不受外力的几何精确梁.其参数[33]如下:梁长l=1,横截面是边长为0.1 的正方形,密度ρ=1000,杨氏模量E=107,泊松比ν=0.35.

取时间步长Δt=10-4s,空间节点数K=10,给定梁的初始对流速度为

初始对流应变为

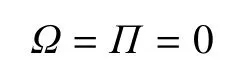
通过Hamel 场变分积分子(8)～(10)迭代计算10 000步,得到几何精确梁的角动量和线动量如图2 和图3 所示,说明了Hamel 场变分积分子可以长时间以O(Δt)精度保持系统角动量和线动量.

图2 梁的角动量Fig.2 Evolution of angular momentum

图3 梁的线动量Fig.3 Evolution of linear momentum

5 结论

对于不受外力、外力矩的力学系统,动量守恒是一个基本的守恒律.对几何精确梁模型,传统方法往往将其看作大量刚体的串联或位形空间为无穷维流形的无穷维力学系统来研究其动量,而本文在协变场论观点下,从时空角度用活动标架法研究Hamel 场变分积分子的保动量性质,进一步说明了Hamel 场变分积分子保结构的性质,同时也间接说明其具有长时间数值稳定性.本文所给的证明方法也同样适用于一般经典场论场景下的Hamel 场变分积分子.下一步将探究Hamel 形式及变分积分子的保能量、保辛结构等保结构性质,并将其应用到壳、膜等更复杂力学系统的建模与仿真中.