基于Edgeworth级数法数控磨床电控系统可靠性指标研究*

范晋伟 刘会普 秦 池 李伟华

(①北京工业大学机械工程与应用电子技术学院，北京 100124；②北京第二机床厂有限公司，北京 102444)

近些年，我国数控机床行业迅速发展，成为数控机床制造大国,目前国产机床可满足大部分用户的使用需求，且价格低廉,然而较之国外数控机床行业，国产机床的性能、精度与可靠性等方面仍存在较大差距，高端机床市场占用率低[1]。数控磨床作为关键数控机床类型之一，广泛应用于航空航天、军事国防和民计民生等精密零部件的加工中，因此，对数控磨床的可靠性建模研究具有重要意义。

国内外学者对数控磨床可靠性建模展开了大量的研究工作：Hoseinie Seyed Hadi利用Weihull函数对液压系统进行了可靠性建模[2]。Ronald R Y利用模糊方法建立了复杂系统的可靠性模型[3]。刘超等人使用最小二乘法对数控磨床冷却系统进行了可靠性建模，确定其符合指数分布模型[4]。罗静等人使用MINIITAB软件对数控磨床故障数据进行可靠性建模，并对其进行了故障树分析[5]。刘勇军等人使用线性回归对数控磨床液压系统进行可靠性建模，并对平均无故障时间进行了点估计和区间估计[6]。黎刚刚对数控磨床砂轮架主轴系统进行FMEA分析,确定其故障部位、故障模式、故障原因及故障影响[7]。

通过以上文献可以发现：数控磨床及其子系统的可靠性研究多为冷却系统、液压系统和主轴系统，电控系统作为数控磨床关键子系统之一，尚未有学者对其进行可靠性指标研究；此外，上述研究方法常利用典型函数分布(正态分布、对数正态分布、指数分布和二参威布尔分布)模型对故障数据进行拟合，即利用线性回归(最小二乘法)进行参数估计，经模型检验和优选后进行可靠性指标计算，存在适用范围小和计算步骤繁琐的缺点。因此，文章引入Edgeworth级数法，结合四阶矩技术和Hermite多项式对数控磨床电控系统进行可靠性指标研究，旨在探索一种新的可靠性指标研究方法。

1 可靠性指标体系

可靠性可以被定义为在使用条件和规定时间内，机械产品完成规定功能的能力，常用的可靠性指标包括：可靠度、累积失效概率、故障概率密度函数和平均故障间隔时间[8]。

1.1 可靠度

可靠度是指在规定时间内，规定条件下，完成规定功能的概率，常用R(t)来表示，是对可靠性的定量描述。计算公式如下：

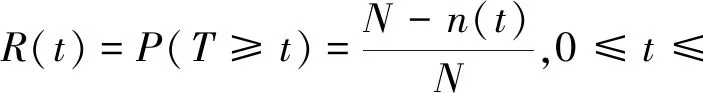
(1)

式中：N为样本总数；n(t)为t时刻时故障样本数。

1.2 累积失效概率

与可靠度相对应，累积失效概率是指在规定时间内，规定条件下，未完成规定功能的概率，也称不可靠度，常用F(t)来表示。计算公式如下：

(2)

1.3 故障概率密度函数

定义累积失效函数F(t)的一阶导数为故障概率密度函数，常用f(t)来表示。计算公式如下：

f(t)=F′(t)=-R′(t)

(3)

1.4 平均故障间隔时间

平均故障间隔时间(MTBF)是指在规定时间内，规定条件下，系统正常运行总时间与总故障次数之比，观察值计算公式如下：

(4)

式中：ti为第i个故障间隔时间；n为故障总数。

引入故障概率密度函数f(t),点估计值计算公式如下：

(5)

2 故障数据的收集

文章的可靠性数据来源于北京第二机床厂MKS型号数控磨床现场实验数据以及部分厂家实际生产过程中记录的数据，在严格遵守《数控机床可靠性评定》[9]中相关原则前提下，共获得364条真实可靠的故障数据，其中电控系统故障数据69条，部分故障数据如表1所示。

表1 电控系统故障数据表

3 Edgeworth级数法

Edgeworth级数法能将服从任意分布类型的概率分布函数近似地展开为标准正态分布，结合四阶矩技术和Hermite多项式，可以获得磨床电控系统的可靠度函数，进而对其他的可靠性指标进行计算。

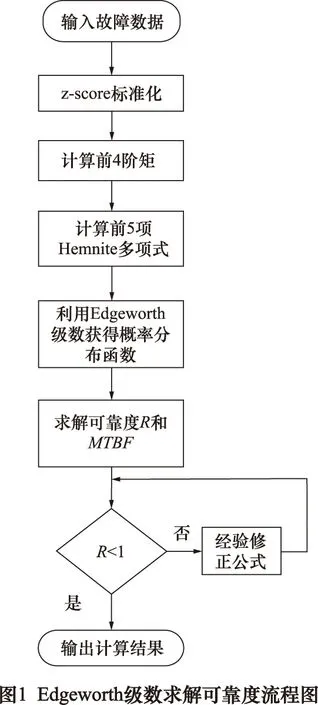
3.1 Edgeworth级数求解可靠度流程

对于任意故障数据t，在引入Edgeworth级数后，其可靠度概率分布函数可展开为以下形式[10]：

(6)

式中：φ(t)为标准正态分布的分布函数，φ(t)为标准正态分布的概率密度函数。μt、σt、θt和ηt为数控磨床电控系统故障数据的前四阶矩，即均值、标准差、偏差和峰度。Hi(t)为第i阶Hermite多项式。相关公式如下：

(7)

(8)

(9)

(10)

θt=E{[t-E[t]3]}

(11)

ηt=E{[t-E[t]4]}

(12)

(13)

利用公式(6)计算可靠度R(t)时，当可靠度R(t)<1可认为Edgeworth级数已获得足够精确的解,但可能出现数据过逼近使得R(t)>1，此时，引入经验修正公式[11]：

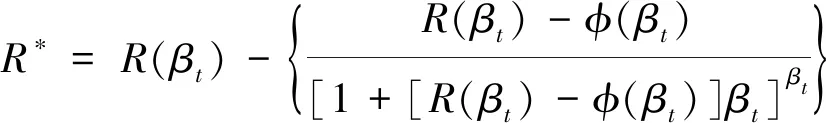
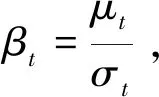
利用Edgeworth级数法求解数控磨床电控系统的可靠度流程如图1所示。

3.2 基于Edgeworth级数法电控系统可靠度计算

按照图2流程图顺序，首先采用z-score标准化法将表1数据进行标准化转换，标准化后故障数据如表2所示。

表2 电控系统标准化故障数据表

由公式(9)～(12)计算得到标准化故障数据的前四阶矩分别为：

(15)

由公式(13)可递推出Hermite第二、第三和第五阶多项式分别为：

(16)

将结论(15)和(16)代入公式(6)，即可得到数控磨床电控系统可靠度概率分布函数为：

0.202 5t3+0.235 7t2+0.190 5t-0.235 7)

(17)

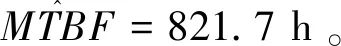
4 传统方法

传统的机电产品整机或关键子系统的可靠性分析思路为：首先将原始故障数据预处理后，然后利用典型函数分布(正态分布、对数正态分布、指数分布和二参威布尔分布)模型对故障数据进行拟合，接下来经模型检验和优选后确定最优模型，最后进行可靠性指标计算。

4.1 传统方法求解可靠度流程

(1)故障数据预处理

常用经验分析法对故障数据进行预处理。对于含有n个增序排列的故障数据，可靠性的估计值可用中位秩计算[12]。可靠度函数R(ti)计算公式如下：

(18)

式中：n为故障总数，i为故障间隔时间。

(2)参数估计

常用最小二乘法[13]对故障数据分布模型进行参数估计，典型分布模型参数估计公式如表3所示：

表3 典型分布函数参数估计表

表3中，a0和a1为线性相关式y=a0+a1x的系数，可由最小二乘法线性回归得到，相关公式如式(19)所示：

(19)

(3)拟合检验

常用D检验法[14](K-S检验法)对模型进行拟合检验，以检验原始数据与拟合曲线之间是否存在线性关系。D检验法相关公式如下：

(20)

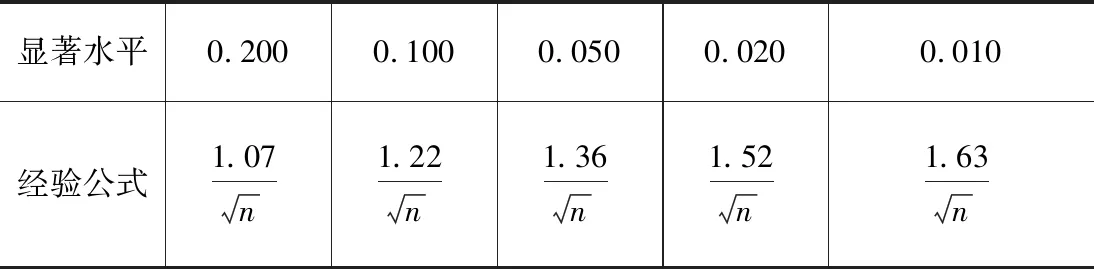
表4 Dn,α经验公式表(n>50)

(4)优度检验

当两种以上模型都经过了拟合检验，为评选出拟合最优的模型，需要对其进行优度检验。常用相关系数法[15]进行模型优度检验，相关公式如下：

(21)

(5)求解MTBF和可靠度R

在确定故障数据可靠性模型后，可按照公式(1)和(5)计算电控系统的可靠度R和MTBF。

利用传统方法求解数控磨床电控系统的可靠度流程如图2所示。

4.2 基于传统方法电控系统可靠度计算

按照图3流程图，首先对故障数据进行预处理，预处理部分结果如表5所示。

表5 经验分析法数据计算表

电控系统典型分布模型拟合的参数估计、拟合检验和优度检验结果如表6所示：

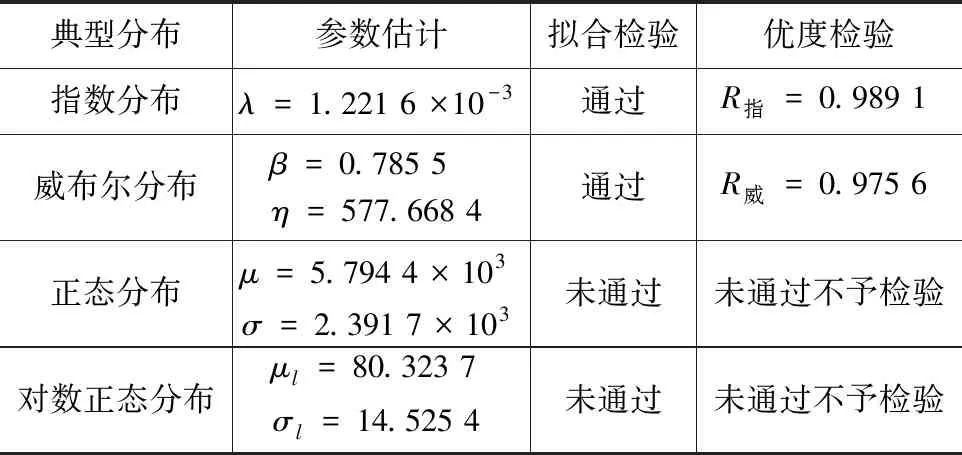
表6 电控系统典型分布模型拟合表

由表6可知：指数分布和威布尔分布均通过拟合检验，且优度R指>R威，则证明指数分布模型对电控系统故障间隔时间的拟合更加精确，可靠性指标如下：

(22)

从两种方法对故障数据可靠度函数拟合效果来看，如图3所示：Edgeworth法在[0,500],[1 000,2 500]区间处比传统方法更加准确。

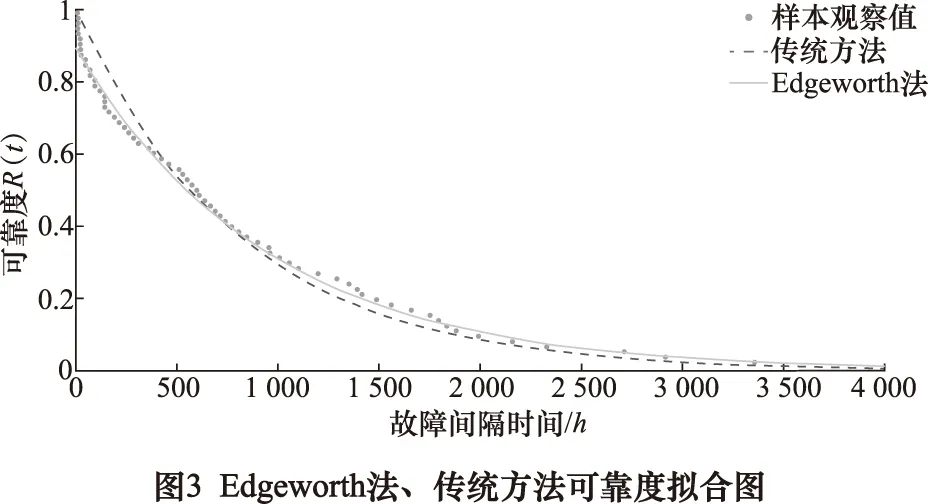
从两种方法MTBF点估计值与MTBF观察值的误差来看，由公式(4)得到MTBF观察值为818.6 h，基于Edgeworth法MTBF点估计值为821.7 h，基于传统方法MTBF点估计值为835.4 h，由此可知，基于Edgeworth法获得的MTBF点估计值更加接近观测值。

5 结语

文章利用Edgeworth级数法对数控磨床电控系统故障数据进行可靠性指标分析。首先结合四阶矩技术和Hermite多项式将电控系统可靠度函数近似展开，计算得到电控系统可靠度函数及其平均故障间隔时间MTBF。然后利用传统方法计算电控系统可靠度函数及其平均故障间隔时间MTBF。最后以故障数据观察值为标准，比较两种方法在可靠度函数拟合和MTBF计算上的优劣。结果显示Edgeworth级数法在保证计算精确性的前提下，能简化电控系统可靠性指标求解过程，克服了传统方法计算过程复杂、运算量大的缺点。研究结果已反馈给厂家并获得认可，对提升数控磨床整机的可靠性水平有重要意义。