基于正交铣削试验的7A65-T7451铝合金表面粗糙度预测模型

武洵德 王文理

(中国航空制造技术研究院，北京 100024)

航空航天领域广泛使用高强铝合金制造关键结构件[1]，7XXX系铝合金历经多个发展阶段，20世纪以来开发出了7075、7475、7050、7055等高强、高损伤容限合金。

近年，欧美在7150、7055等高强韧铝合金的基础上，进一步研究发展出的更高强度级别、断裂韧性和耐腐蚀性能更加优异的新一代高强高韧性和高强高耐蚀铝合金。

国内针对性的开发出了7A65系新型铝合金，在25～100 mm和100～152 mm厚度区间，7A65铝合金厚板强度及断裂韧性均较7050厚板有较大幅度的提升，强度分别提升了10%和13%左右，断裂韧性高出20%以上。其他各项性能包括疲劳、应力腐蚀等仍保持了7050厚板的综合优势。使用7A65铝合金替代航空飞行器机体材料使用量最大、使用部位最多的7050铝合金，可以起到5%～10%的减重作用。7A65铝合金具有高强度、高韧性等优势，将成为未来航空航天领域高端装备制造同类铝合金材料和各大军民用飞机主承力结构件的升级换代成品，拥有广阔的应用前景。

表面粗糙度是衡量航空结构件加工质量的重要指标，对零件的耐磨性、疲劳强度及抗腐蚀性等使用性能有直接影响[2-3]，表面粗糙度是表面完整性最重要的因素[4]，也是影响航空器疲劳寿命的主要因素[5]。

目前国内外主要使用回归分析法、响应曲面法和神经网络等方法构建切削参数和表面粗糙度的关系模型。王素玉[5]、任敬心[6]、陈曦[7]等人利用回归分析方法进行了粗糙度模型的构建，陈涛等人[8]使用反应曲面法建立切削轴承钢的粗糙度模型，Kumar V[9]和Sethupathy A[10]等人也利用响应曲面法建立了精度较高的表面粗糙度数学模型，刘红军和杨树新[11]建立了一种基于改进粒子群神经网络的铣削表面粗糙度预测模型，Krishna Mohana Rao G等[12]采用神经解包建立了多感知器神经网络模型并对网络的权重因子进行了优化。基于回归分析法简单与直观的优点，本文使用回归分析法建模。

由于国内尚无7A65-T7451铝合金的加工经验，缺少切削工艺参数和工艺特性，本文采用正交试验方法对7A65-T7451铝合金厚板材料进行大量切削试验，测量表面粗糙度参数，利用多元回归分析法建立表面粗糙度预测模型，研究铣削参数对表面质量的影响规律，为未来7A65-T7451铝合金的铣削参数优化和7A65铝合金飞机结构件加工提供了试验参考依据。

1 切削试验

1.1 正交试验设计

如果进行完全试验方案，试验过程复杂且试验数量将高达74次，因此采用统计学家田口玄一的正交试验法简化过程，可获得较好的试验效果。本试验选用四因素七水平正交试验，以获得大量的工艺数据。根据标准正交表L49.7.8，处理以后得到正交试验方案见表1。

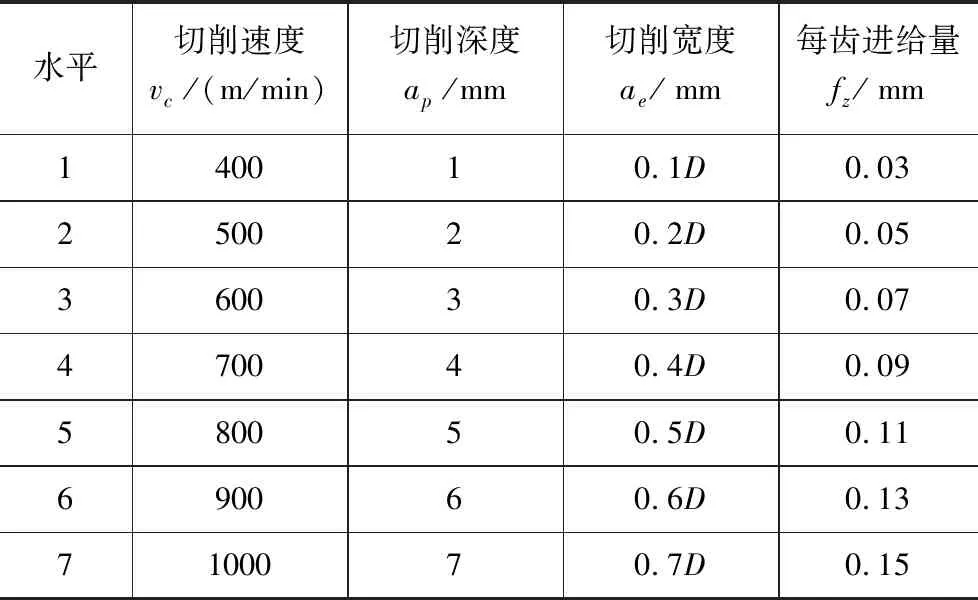
表1 四因素七水平正交试验参数优化方案

1.2 刀具选择

本试验使用山特维克可乐满(Sandvik Coromant)CoroMill Plura整体硬质合金立铣刀，材料牌号为H10F，刀具规格见表2，适于铝合金铣削。

表2 试验刀具规格

1.3 试验材料

试验工件为7A65-T7451铝合金预拉伸板，规格为500 mm×600 mm×80 mm，对7A65-T7451铝合金板材合金元素分析，并与7050-T7451铝合金作比较：7A65-T7451铝合金的Zn元素的含量有所提高，Cu元素含量变化很小，Mg元素和其余微量元素含量有所下降，导致7A65-T7451铝合金的强韧性较7050铝合金提高了10%左右，硬度也有较大变化，试验材料硬度采用便携式硬度测量仪(图1)现场测量得到，数据见表3。

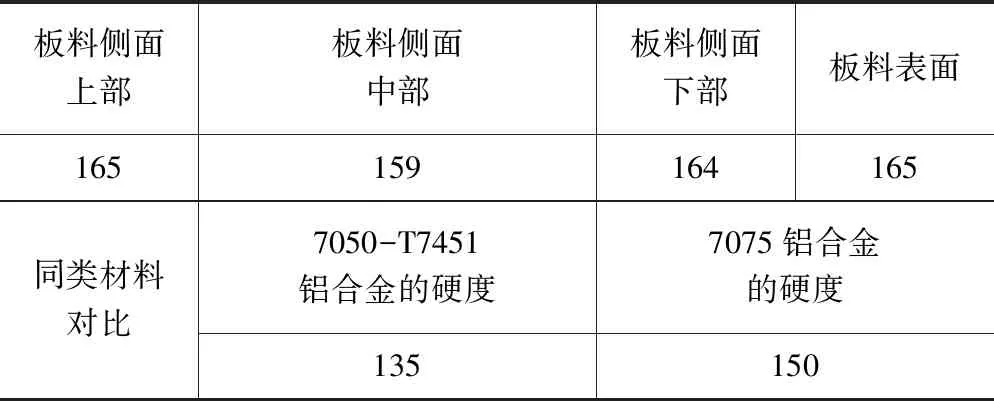
表3 7A65-T7451铝合金δ80预拉伸板硬度(HBW，10 mm/3 000 kg)

1.4 试验设备

HSM25-80五坐标桥式高速铣床(主轴最大转速24 000 r/min，主轴最大功率44 kW，主轴最大扭矩62.7 N·m)，采用SINUMERIK-840D数控系统，试验现场如图2。试验中测量表面粗糙度采用TIME/时代TR220手持式粗糙度测量仪(图3)，测量范围：Ra0.025～12.5 μm，测量精度：0.001 μm。

1.5 试验现场及结果

试验在HSM25-80高速铣机床上进行，采用喷雾冷却，试验过程采用顺铣行切方式进行切削，试验走刀及实际切削现场和结果如图4和图5所示。

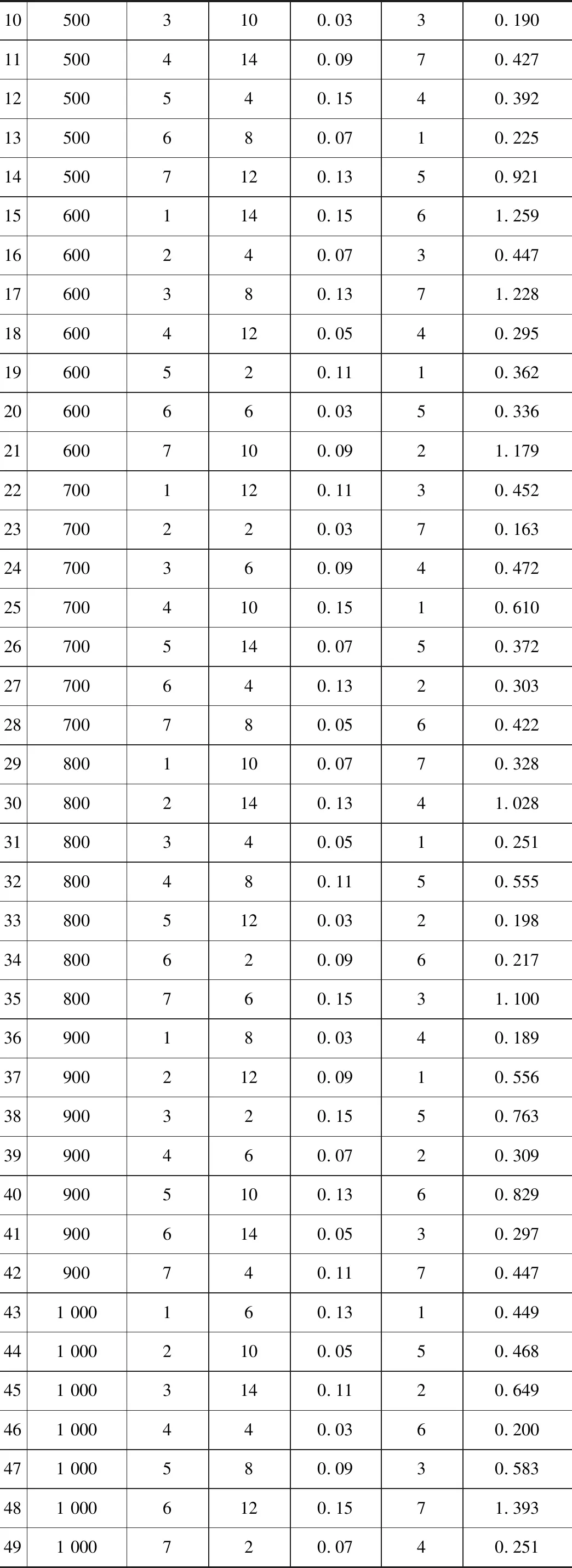
在现场切削试验过程中，根据实际切削效果和现场条件，每组试验后取2～3个不同区域重复测量获得多次测量结果，计算其平均值作为该组试验的最终结果，最终试验结果见表4。

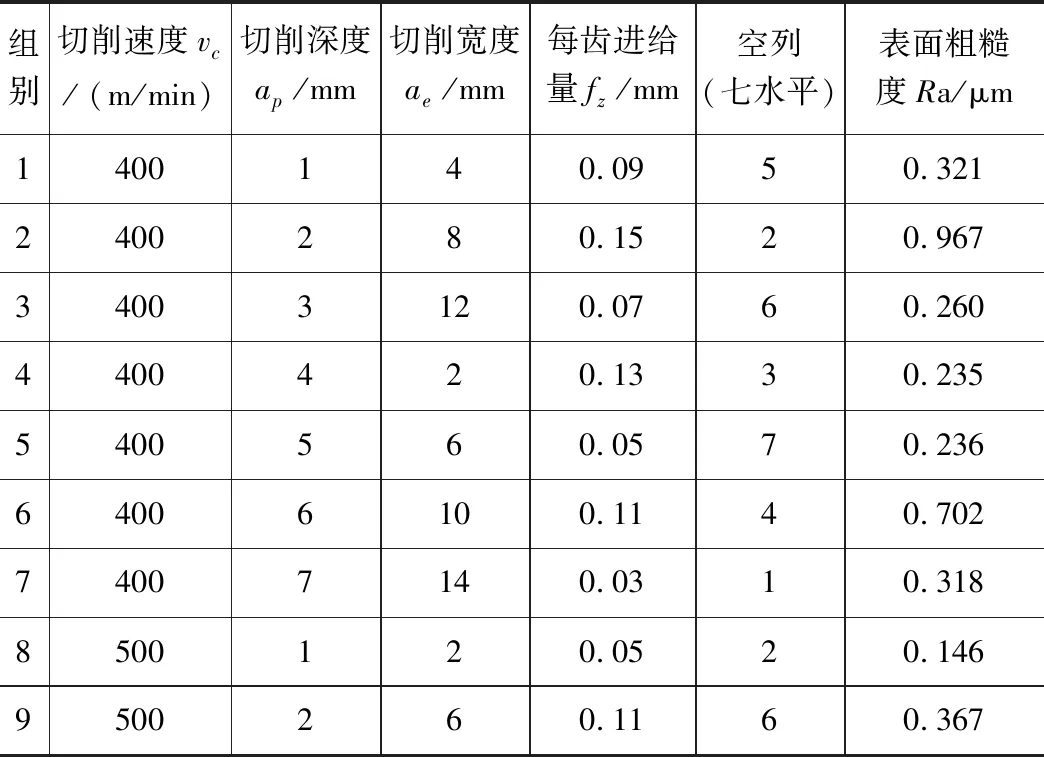
表4 正交切削试验结果

105003100.0330.190115004140.0970.42712500540.1540.39213500680.0710.225145007120.1350.921156001140.1561.25916600240.0730.44717600380.1371.228186004120.0540.29519600520.1110.36220600660.0350.336216007100.0921.179227001120.1130.45223700220.0370.16324700360.0940.472257004100.1510.610267005140.0750.37227700640.1320.30328700780.0560.422298001100.0770.328308002140.1341.02831800340.0510.25132800480.1150.555338005120.0320.19834800620.0960.21735800760.1531.10036900180.0340.189379002120.0910.55638900320.1550.76339900460.0720.309409005100.1360.829419006140.0530.29742900740.1170.447431 000160.1310.449441 0002100.0550.468451 0003140.1120.649461 000440.0360.200471 000580.0930.583481 0006120.1571.393491 000720.0740.251

2 数据分析与建模

2.1 数据分析

利用简单且实用性强的极差分析法(R法)处理试验结果(式(1))，以此来确定正交试验中各因素影响指标的主次关系排序，同时确定本次试验中各因素的最优水平、找出试验结果范围内的最优组。极差分析结果见表5。

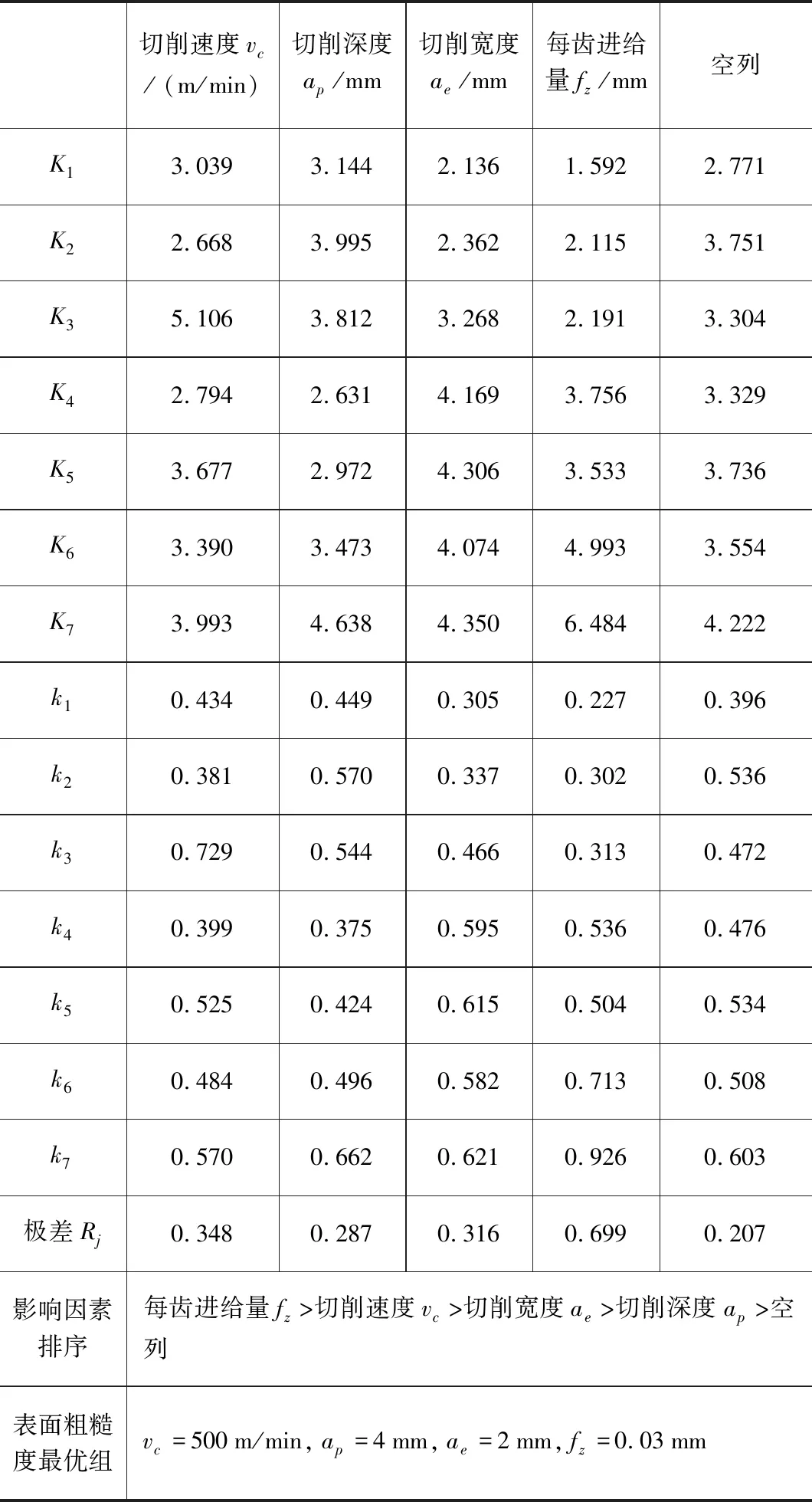
表5 极差分析结果

(1)

极差分析结果显示，各切削参数中每齿进给量fz对表面粗糙度有最显著的影响，切削速度vc和切削宽度ae次之，切削深度ap的影响最小。现有试验分析结果的表面粗糙度最优组见表5中结果。

根据试验结果分析平均值水平的变化，绘制基于均值的切削参数对表面粗糙度的影响趋势图(图6)。

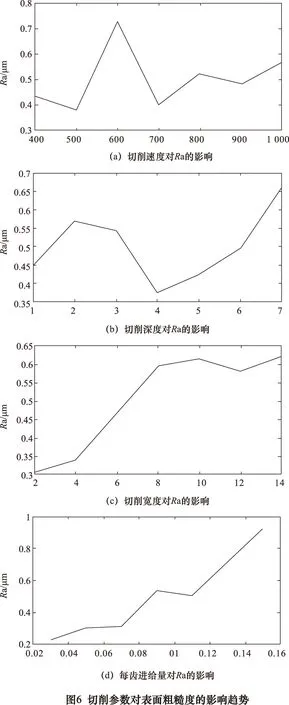
在图6a和b中，切削速度和切削深度对表面粗糙度的影响基本都是在前段存在一个峰值区，然后逐渐增加，实际加工中尽量避开峰值选取参数。根据图6c和d，表面粗糙度与切削宽度和每齿进给量基本呈正相关增加的趋势，实际加工推荐使用较小的进给量和切削宽度。加工选取参数时，应避免同时使用大切削参数，以提高机床和刀具的使用寿命。

2.2 粗糙度预测模型

根据Tipnis V等的加工表面粗糙度预测的经验模型[13]，该模型包含了切削速度、进给量及切削深度3个切削参数，Yang A[14]和Ramesh S[15]等人对影响切削加工表面粗糙度的因素进行研究和验证，以此模型和本试验数据为基础，还需要在模型中加入本试验所用到的切削宽度因素，因此应用正交回归试验建立表面粗糙度与切削用量之间的指数关系式[15]。

(2)

式中:Kr为决定于加工材料、切削条件的修正系数；n为主轴转速；ap为轴向切深(切削深度)；ae为径向切深(切削宽度)；fz为每齿进给量；b1、b2、b3、b4为指数。对式(2)两边取对数

logRa=logKr+b1logn+b2logap+b3logae+b4logfz

(3)

式(3)可以转化为

y=b0+b1x1+b2x2+b3x3+b4x4

(4)

建立多元线性回归方程

式中：εi为试验随机变量误差。

式(5)用矩阵形式表示为

Y=Xβ+ε

(6)

其中

Y={y1,y2,y3,…,y49}T

β={β0,β1,β2,…,β4}T

ε={ε1,ε2,ε3,…,ε49}T

采用最小二乘法对参数β进行估计，得到回归方程为

(7)

b=(XTX)-1XTY

(8)

根据表4计算得到

得到

b={-0.519 0，0.234 7，0.076 1，0.380 4，0.797 8}T

因此铣削7A65-T7451铝合金厚板的表面粗糙度预测模型为：

(9)

3 预测模型的显著性检验和误差检验

3.1 回归方程的显著性检验

根据经验公式假设得到模型，但仍要判断模型的拟合程度，对其进行显著性检验，以判断模型拟合的状态。

统计检验结果如表6所示，F=25.396>[F(4，40)，F(4，60)]，显示本试验表面粗糙度预测模型是高度显著的，拟合状态较好，有较高的可信度。

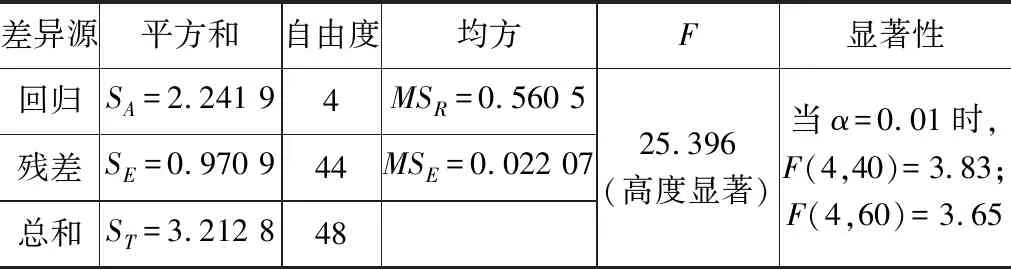
表6 表面粗糙度回归方程显著性检验分析

3.2 预测模型的误差检验

除了正交试验以外，试验中还进行了其他试验组进行试刀分析，使用这些试验数据进行表面粗糙度模型的准确度和误差验证，以此来评价回归分析得到的模型是否具有实践意义，能否对实际加工进行工艺指导。

表7是验证参数及模型计算参数的汇总对比，根据误差计算结果，误差平均值为11.68%。误差结果显示该预测模型的预测准确度较好，在实际生产现场具有一定的指导意义。同时从检验结果观察到，在实验参数范围内插的预测结果比外拓的预测值要好一个数量级，处于模型参数范围内的预测效果是比较好的。工程应用如果需要更全面的预测模型，可以适当增大试验组参数范围进一步优化模型。

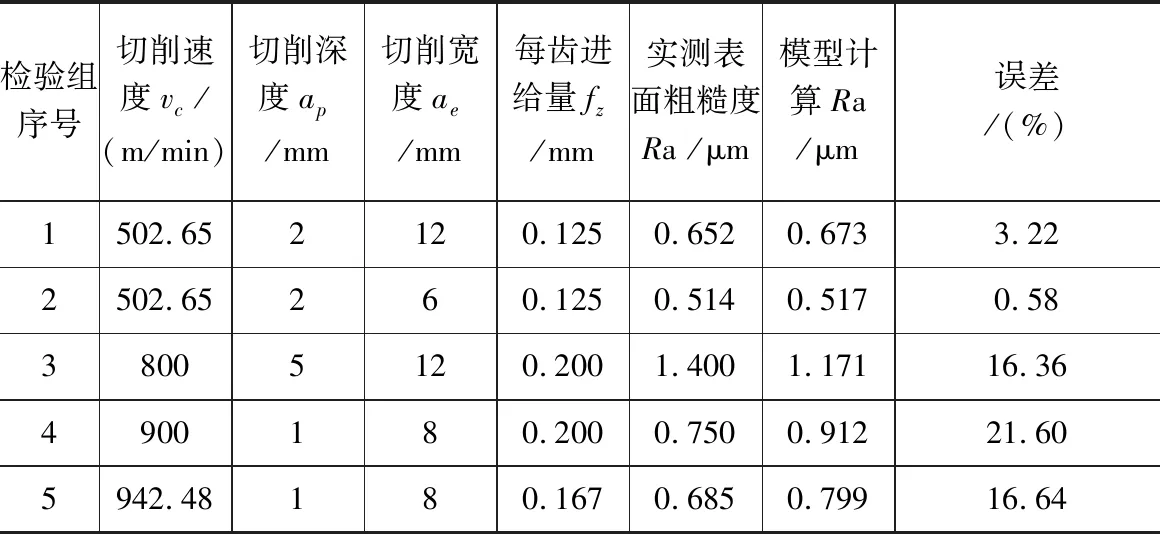
表7 检验参数及结果与模型预测值对比误差

4 结语

对7A65-T7451铝合金预拉伸板进行表面粗糙度正交铣削试验，使用极差分析法确定各切削参数影响权重和本试验表面粗糙度最优组，确定各切削参数对粗糙度的均值效应影响趋势，利用多元线性回归进行建模，建立7A65-T7451铝合金表面粗糙度预测模型，得出以下结论。

(1)7A65-T7451铝合金在国内缺少相关的切削试验参数，本试验填补了相关领域的工艺参数空白，为7A65铝合金飞机结构件加工提供了基础切削参数和经验，对7A65铝合金的应用推广有借鉴意义。

(2)本试验建立的预测模型基于现场正交试验和回归分析，针对7A65-T7451铝合金的厚板切削，根据实际拟合效果和误差检验结果，模型准确度和可信度较高，有一定的工程应用价值。

(3)依据表面粗糙度预测模型，可以在本试验参数范围合理选择加工参数提高7A65-T7451铝合金零件表面粗糙度，以此提高飞机结构件的疲劳寿命。