基于局部搜索的并行扩展规则推理方法∗
李 壮,刘 磊,张桐搏,周文博,吕 帅
1(吉林大学 计算机科学与技术学院,吉林 长春 1 30012)
2(符号计算与知识工程教育部重点实验室(吉林大学),吉林 长春 130012)
可满足性问题(SAT)是公认的第一个NP-完全问题,是人工智能领域最重要的研究方向之一.自人工智能发展初期就引起了研究者的广泛关注,当今SAT 求解器已能够解决很多现实问题.近年来,国内外的学者致力于求解SAT问题的效率和求解能力,提出了多种方法.
1992年,Selman 等人提出的GSAT 算法证明了局部搜索算法可以应用于求解SAT 问题,其强大的求解能力为局部搜索求解SAT 问题奠定了基础[1].随着局部搜索方法在该领域的广泛应用,自2002年SAT 比赛的开展以来,众多基于局部搜索算法的求解器也相继问世并展现出了各自强大的求解能力.2005年,Li 等人提出了g2wsat类算法,该算法结合随机选择和贪心双模式,在求解的过程中展现出良好的性能[2].2011年,Li 等人提出了利用变量可满足历史记录的局部搜索求解器SatTime,获得SAT 2011 随机组银奖[3].2016年,KhudaBukhsh 等人提出了SATenstein 求解框架,该框架结合了多个高性能局部搜索求解器,其求解效果胜过多个主流求解器[4].近年来,由Cai 等人提出的基于局部搜索的格局检测策略成为SAT 比赛中最具影响力的策略之一.2011年,Cai 等人设计的SWCC 算法及相关求解器皆使SAT 求解器的计算能力得到巨大地提升,并取得惊人的成绩[5].随后,Cai 等人于2012年提出的CCASat 获得SAT 20 12年随机组金奖[6].2014年,Cai 等人提出的CSCCSat 获得SAT 201 4年比赛Hard-combinatorial 组铜奖和SAT 2016 比赛Random track 组银奖[7].同时,基于局部搜索的格局检测策略用于求解Max-SAT 问题也取得了巨大的成功[8,9],其中,CCLS 在MAX-SAT 2013 非完备性求解器组中获得4 项金奖.2018年,Cai 等人基于局部搜索算法,在完备算法上设计了ReasonLS 求解器,并在同年SAT 国际比赛中获得No-Limits track 组金奖[10].以上不难看出,局部搜索算法的广泛应用和强大的效率已得到不断突破.
经典的SAT 求解器大多基于DPLL 算法和归结方法,2003年,Lin 等人提出的扩展规则方法打破了传统思维的限制,开辟了SAT 求解的新思路[11].作为归结方法的互补方法,通过寻找子句的极大项来判断CNF 公式的可满足性.他提出的ER 算法得到了国内外的广泛认可,并为日后的研究打下了坚实的基础.基于ER 的算法,Lin、Wu、李莹和张立明等人分别提出了IER[11],RER[12],NER[13],SER[14]等算法,将完备的ER 算法的求解效率提升了几个数量级的高度.在扩展规则的应用方面,2010年,殷明浩等人在可能性扩展规则的基础上提出了EPPCCCL理论,可作为可能性知识编译的目标语言[15].2016年,刘磊等人提出了扩展反驳方法,并在该推理方法与知识编译之间建立了联系[16].2017年,王强等人提出两种加速#SAT 求解的启发式策略,提出了CER_MW 和CER_LC&MW 两种算法,其求解速度是其他算法的1.4 倍~100 倍,求解能力也在限定时间内可解更多的测试用例[17].2018年,杨洋等人在SWCC 算法的基础上提出了ERACC 算法,该算法突破了传统扩展规则推理对公式规模的局限,求解效率有了极大提高[18,19].
不仅如此,各种经典的技术也相继应用于扩展规则求解的过程中,如启发式和并行处理等技术.2009年,李莹等人针对IER 算法提出了IMOM 和IBOHM 两种启发式,其求解效率较IER 提高了10 倍~200 倍[20].Zhang等人基于其PSER 的半扩展规则策略提出了分割解空间的PPSER 算法,证明了该算法具有合理的执行效率,并优于NER、DR、IER 等算法[21].
由以上不难看出,基于扩展规则的推理方法如今已得到了广泛的应用.但与局部搜索等推理方法相比,仍然具有很大的提升空间和完善度.本文基于ERACC 算法,从李莹的IMOM 启发式算法和张立明的PPSER 并行算法中得到启示,提出了PERACC 算法.该算法基于杨洋等人[18,19]的ERACC 算法,调用启发式算法CPVI,通过选择变量并调用PERM 算法,用变量的组合将原解空间分割成不同的子空间,每个子空间通过SIMT 算法选择初始极大项,随后进行并行处理.最后实验证明,该算法较ERACC 算法的求解效率有较大的提高[22].
本文第1 节介绍了局部搜索和扩展规则的基础知识并给出了相关定义.第2 节提出启发式策略CPVI 算法、并行处理策略PERM 算法和变量赋初始值策略SIMT 算法,并将它们有机结合,在ERACC 算法基础上提出了PERACC 算法.第3 节进行了实验的对比,证明了我们的算法在特定的问题上较原算法快出1.6 倍~117 倍不等.
1 基础知识
1.1 局部搜索
定义1.在一个布尔变量集合V={x1,x2,…,xn}中,每个变量呈正、负两种文字形式xi和¬xi以析取的形式存在于CNF(conjunctive no rmal form)公式的每个子句Ci中,公式中的每个子句之间是合取的.找到一个或多个解释能使CNF 公式为可满足的真值指派过程,称为SAT 求解.
SAT问题的求解是按照某种特定规则对变量进行选取、赋值和剪枝等过程,找到可满足的解释.完备的算法如DPLL,其功能在于不仅可以判断子句集的可满足性,而且可以找到可满足的解.局部搜索作为不完备的方法采取完全不同的方式对SAT 问题进行求解,该方法通过不断变换部分子句空间所有变量赋值使得可满足的子句不断增加,最终达到子句集可满足的目的.当处理不可满足的问题时,由于子句集无解而使变量赋值无限地变换下去.因此,局部搜索只能求解可满足的子句集,且其求解效率远高于完备的算法,却无法处理不可满足的子句集.
1.2 扩展规则
传统的归结方法是通过归结出空子句来判断子句集不可满足;而作为归结的互补方法,扩展规则是通过对CNF 公式中的子句能否扩展出所有极大项来判断其可满足性.其基本定义如下.
定义2.CNF 公式中的一个子句C,变量l的文字形式不在C中出现.有D={C∨l,C∨¬l},则称C到D的过程为扩展规则,D是子句C关于变量l扩展后的结果.
定义3.若一个子句包含所有变量对应的正文字或负文字之一,则称该子句为变量集的一个极大项.
初始的扩展规则推理方法是通过计数每个子句所能扩展出的极大项个数,利用容斥原理计算所能扩展出极大项总数.如果极大项个数是2n(n为变量个数),则CNF 公式是不可满足的;否则是可满足的.这种完备算法的缺点在于:其处理的CNF 规模十分有限,当子句数超过一定阈值,将会造成内存溢出.李莹等人提出的NER 算法通过一定次序判断当前极大项T是否能被CNF 公式中的子句扩展出来:当所有极大项都能被扩展出来时,子句集不可满足;当存在至少一个极大项不能被扩展,则子句集可满足.该算法的求解效率远优于ER 和IER 算法,但缺点在于机械地变换极大项,暴力的求解方式满足了算法的完备性,却丢失了很多启发式信息.杨洋等人提出的ERACC 算法基于局部搜索的格局检测方法,通过得分机制选取变量,根据变量的邻居关系精确格局信息,并通过双向半扩展规则来限制变量的选取范围.该算法在时间复杂度和空间复杂度上都有了很大的改进,并且利用了局部搜索的高效性,使求解可满足问题的求解效率达到了质的飞跃.
1.3 基于精确格局检测的扩展规则算法
基于局部搜索的扩展规则推理方法的本质在于:以寻找极大项空间不可扩展的极大项为目标,利用贪心策略限定极大项空间,以变量的邻居变量设定格局信息,从而减少了冗余搜索步骤,牺牲了算法完备性,从而达到了高效求解的效果.
ERACC 算法的精髓在于对极大项中反转变量的选择,通过最大左度和最小右度的概念,限定两集合中的变量.如果集合为空,则退一步选择得分高的变量取反.精确了变量的选择直接控制了极大项的变换,使得推理过程更加精确(算法的具体流程见文献[18,19]).但是算法仍存在以下不足:初始极大项的选择并没有明确的启发式;串行的处理也使得ERACC 算法无法发挥出极致的效果;忽略了预处理技术,使子句集没有化简的过程.下文将针对以上问题提出PERACC 算法,使求解的性能发挥到极致.
2 PERACC 算法
传统的基于扩展规则的并行推理方法将子句集的极大项空间分解为若干个子空间,并对其进行逐一求解.这种并行方式并未加入启发式信息,使得分割空间无层次.即使分割的子空间彼此毫无关联,但整体推理的空间复杂度并无降低.
本文提出的并行处理是一种结合了对解空间化简的预处理方法.在选择特定的变量之后,对原子句集进行化简,化简后的子句集与原子句集是逻辑等价的,这也极大地降低了对整个子句集求解的空间需求;并在ERACC 算法中加入了对初始值的赋值限制,改变了ERACC 对初始值赋为1 的单调做法,使求解器整体求解能力得到了较大地提升.
2.1 CPVI算法
我们通过选取变量的启发式算法,对出现在每个子句中的文字赋予权值.从文字出现在各个子句中的累计次数计算出得分最高的变量.首先,遍历原始子句集获得所有文字的数组,从数组中选取最大数对应的变量.如果同等数量的变量有若干个,那么从中随机选取需求个数作为初始变量,变量个数由所划分的解空间参数决定.变量选取算法如下,其中,vs=(var,score)表示变量及对应的得分,其中,var表示变量,score表示变量的得分.
算法1.计算选取的变量CPVI(computing the picking variables initially).

算法1 采取一种遍历求和排序的方式来计算各个变量的得分集合,从而选取权重最高的变量作为化简子句集的初始变量.算法第2 行表示程序遍历了整个子句集F并统计了所有变量集合;第3 行~第5 行对所有的变量及其得分清零;第6 行~第10 行分别描述了对所有变量和每个变量在各个子句中的双重循环,得到变量集合的得分数组vsi.score,并对其进行排序;第12 行~第24 行表示当出现得分均等的若干个变量时,从中随机选取所需个数变量;最后输出所选择的变量.
变量得分的计算,令F为CNF 公式,Ci={l1,…,lk}为子句集中任意子句(i∈(0,m]),m为子句数,Wi为子句相关联文字的权值.则变量v基于F的得分函数为
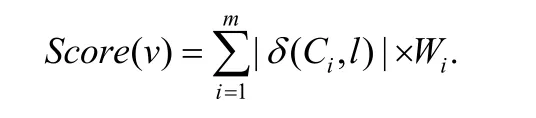
在以上公式中,δ为二元谓词特征函数,代表多值逻辑的取值.令l表示在子句Ci中变量v所对应文字的取值.δ的具体定义如下:

以上公式给出了变量得分的计算方式,基本思想为:根据文字出现在子句中的形式取相应的值.正文字取1(变量所对应文字为l时取1),负文字取−1(变量所对应文字为¬l时取−1).通过求和计算累计变量的得分,根据得分将变量排序,进而选取所需变量.该方法的时间复杂度是线性的,因此,该预处理方法所需时间在求解的过程中所占比重是极小的.
例1:令CNF 公式F={A∨C∨¬D,¬B∨¬G∨H,¬A∨E∨G∨¬H,C∨E∨H,¬D∨G∨¬H},在该测试用例中,每个变量相对应的文字权值Wi为1,则变量的得分如下:
•Score(A)=|1×1|+|0×1|+|(−1)×1|+|0×1|+|0×1|=2;
•Score(B)=|0×1|+|(−1)×1|+|0×1|+|0×1|+|0×1|=1;
•Score(C)=|1×1|+|0×1|+|0×1|+|1×1|+|1×1|=2;
•Score(D)=|(−1)×1|+|0×1|+|0×1|+|0×1|+|(−1)×1|=2;
•Score(E)=|0×1|+|0×1|+|1×1|+|1×1|+|0×1|=2;
•Score(G)=|0×1|+|(−1)×1|+|1×1|+|0×1|+|1×1|=3;
•Score(H)=|0×1|+|1×1|+|(−1)×1|+|1×1|+|(−1)×1|=4.
由例1 可以看出:给定CNF 公式F中,所有文字的权值为1,在对变量选择的过程中扫描一次即可得知变量的得分.在选取变量阶段,我们选取得分最高的变量(例1 中的变量F).在硬件条件允许的条件下,我们可以选择多个变量.如果我们选择3 个变量,那么会根据得分依次选择变量G和变量H,而第3 个变量的选取则在得分相等的变量{A,C,D,E}中随机选取一个.
我们的目的在于对原解空间进行最大程度化简,因此选择了得分最高的变量作为初始变量.最理想的情况是存在某个变量出现在每个子句中,这样可以最大程度地降低子句集规模,得到的问题规模最小.即:在预处理阶段约简了原子句集,其约简后的结果与原子句集是逻辑等价的.
定理1.预处理阶段,化简后的子句集与原子句集是逻辑等价的.
证明:固定了极大项中的文字之后,原子句集中带有互补文字的子句可直接忽略,因为这样的子句是无法扩展出当前极大项的;而带有相同的文字可以忽略不计,只看除了该文字剩余部分的子句.这样,剩余变量的模型组成了新的极大项,与化简后的子句集相对应,即,同原极大项和原子句集是逻辑等价的.
例2:令CNF 公式F={A∨B∨C∨D,¬A∨B∨¬C∨E,¬A∨¬B∨¬G,¬A∨B∨¬D∨¬E,B∨C∨¬D∨G},按照算法1 选取变量,我们应选择的变量为A和B.如果我们单看其中的一个子空间,变量取值为¬A和B,那么化简的原子句集为F′={¬C∨E,¬D∨¬E,C∨¬D∨G},新的解空间是由变量{C,D,E,G}所组成的极大项空间.
由例2 可以看出:在保证了逻辑等价的前提下,化简后的子句集规模已经远远地小于原子句集的规模.实验证明:不论在时间还是空间上,都有了很大的提高.
2.2 PERM算法
选择变量的目的在于化简解空间,而并行的目的是基于化简基础上能够全面地对子句集求解.由于选择的变量组合的不同,对子句集化简的程度也不同.基于该问题,我们会选择几种化简后,求解效率最高的那个子空间作为判断的标准.我们提出了PERM 算法来解决这一问题.
PERM 算法过程如下:
算法2.并行扩展的推理方法PERM(parallel extensionrulereasoning method).

算法2 给出在极大项子空间中分割原始极大项解空间的并行算法PERM.首先输入原CNF 公式和已选取的变量,预处理程序通过二进制方法将变量的2α种析取将子句集的极大项空间分解为threadnum个独立的子空间,并记录每个子空间的返回结果,然后对每个极大项子空间并行地调用ERACC 算法进行极大项的判定.当某一个极大项子空间EndThread(i)中返回的结果为SAT,即该子空间中存在某个极大项在规定时间内不能被扩展出来的子句,则子句集是可满足的.将该结果返回至主程序,推理过程结束.
2.3 SIMT算法
由第1 节我们可知,NER 和ERACC 两种算法都是以寻找子句集扩展不出的极大项为目标来进行推理的,所以我们采取的途径是变换和调整极大项的模型.在ERACC 中已详细地说明了如何去变换调整极大项,忽略了对初始极大项的重视,采用了单纯的对初始极大项中没个变量赋值为1.初始的极大项中,变量的赋值在整个推理过程中占据重要的位置.如果没有针对性地给初始极大项赋值,则会在求解过程中走很大的弯路,间接地增加了冗余的推理过程.
为了使推理过程更直接、高效,我们提出了SIMT 算法,有针对性地解决对初始极大项中变量赋初始值的选择.由于极大项中的每个变量可以赋值为正和负两种文字形式,而每种文字形式的赋值概率为50%,我们提出的算法是每个变量根据原子句集中文字出现的比率来确定初始极大项中变量的取值概率.实验结果表明,我们的策略是有效的.
SIMT 算法过程如下.
算法3.选择初始极大项方法SIMT(selection of initial maximum term).


算法3 中,i代表初始的极大项,通过遍历子句集得到F中的变量数n,再根据每个变量所对应的文字统计其正、负文字出现的个数,n(li)表示变量对应的文字总个数.第5 行~第10 行是一个循环.根据正负文字出现的个数与变量对应的文字总个数,计算对应极大项中该变量应该赋值的概率,即有指向性地调整了变量赋值的概率.逐一对变量赋值之后,当赋值变量的个数完成了第n个后,说明初始极大项已经产生,算法结束.有针对性地选择初始极大项,会使下一步的推理更加精准,提高了推理效率.
2.4 PERACC算法
结合了以上算法,基于ERACC 算法,我们提出了基于精确格局检测的并行扩展规则算法,算法过程如下.
算法 4.基于精确格局检测的并行扩展规则算法 PERACC(parallel e xtension rule ba sed on accurate configuration checking).

算法PERACC 的执行过程大致如下:第1 行~第4 行通过调用CPVI 算法选择初始变量,通过变量选择的数量,得到分解解空间的数量,并对各个解空间进行化简,然后对各个解空间进行求解;第5 行调用算法SIMT 来计算各个解空间的初始极大项;第6 行~第18 行是调用ERACC 算法对每个解空间的求解,其详细过程可参考文献[18,19];第19 行~第22 行是一个死循环,当各个解空间中,某一个解空间找到了扩展不出的极大项,那么跳出该循环.
3 实验结果与分析
本节对算法PERACC 算法进行实现,并且将其与扩展规则领域主流的求解器SER,ERACC 以及国际主流的SWCC 求解器进行了对比.实验结果证明了PERACC 算法不仅胜过了传统的扩展规则方法,而且大大地缩短了与国际主流求解器的距离.
实验环境:Arch Linux 16.04 操作系统,12 核CPU,内存8GB.对于每一问题测试用例,均将算法执行50 次,最终取平均值作为结果.由于本文提出的算法属于不完备算法,所以解决的问题都是可满足性的问题.测试用例来源于https://www.cs.ubc.ca/~hoos/SATLIB/index-ubc.html,SWCC 的源代码来源于他的个人主页https://lcs.ios.ac.cn/~caisw/SAT.hrml,g2wsat 的源码来源于国际SAT 比赛官网https://www.satcompetition.org/.
首先,我们采用处于相变区域的Uniform Random-3-SAT 问题,不论是对于系统的SAT 求解器或者是随机的局部搜索算法都是很难的问题.在以往的扩展规则算法测试中,由于受到求解规模的限制,只能求解一些小规模的测试用例.而在文献[18]中,ERACC 求解器已经展现出了其强大的求解能力,可以求解先前求解器无法求解的测试用例.所以在我们的测试中,首先选择了ERACC 所能求解的规模最大的测试用例.我们选择变量250、子句数为1 065 的规模最大的问题.由于测试用例规模较小,所以该组实验我们将运行30 秒未结束的测试用例定为Time o ut.由表1 不难看出:传统的SER 算法已经无法解决规模庞大的测试用例,而ERACC 算法和PERACC 算法显然已经突破了传统算法的限制,发挥了极大的潜力.在这组测试用例中,PERACC 算法的求解效率并没有ERACC 好.原因在于预处理的过程需要少量的时间,而ERACC 算法没有预处理的过程.因此,在处理规模相对较小的问题时,并不能凸显出PERACC 算法的优势,即先前所能求解的测试用例已经无法凸显我们算法的优势.
在表1 实验中,我们默认PERACC 算法在预处理过程中选择4 个变量,并不确定选择4 个变量就是最优的选择.
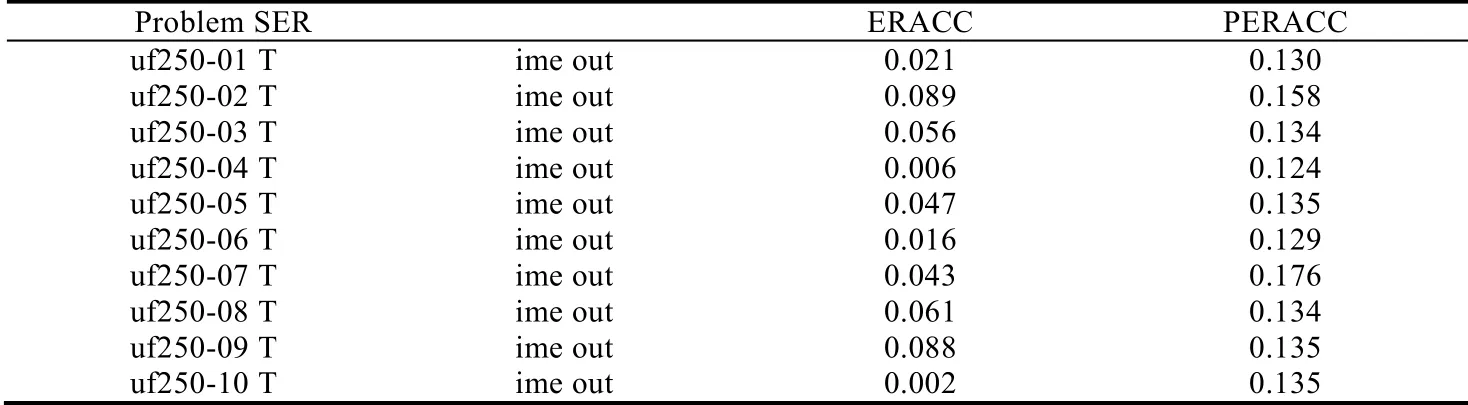
Table 1 Experiment results on uniform random-3-SAT instances uf250(CPU time/s)表1 随机3-SAT 测试用例uf250 实验结果(CPU time/s)
带着以上两个问题,我们做出了以下实验.
表2 选择了图着色问题中一些较难的大型Random-3-SAT 测试用例.图着色类测试用例包含200 个顶点和479 条边,将GCP 测试用例编译为SAT 问题后,成为600 个变量和2 237 条子句.我们选择以下测试用例的原因在于它们的复杂性更高,求解时间较长,所以该组实验我们将运行500 秒未结束的测试用例定为Time o ut.这些测试用例与表1 相比规模更大,更能突出PERACC 的性能,符合我们对上述问题的实验论证.
为了测试SIMT 算法的有效性,我们在表2 中加入了基于ERACC 算法,结合了SIMT 的算法ERACC+.通过ERACC 和ERACC+两组实验我们不难看出:在21 个测试用例中,ERACC+组有18 个测试用例优于ERACC 组,其中效果最好的一组对比数据提高了82 倍.而平均时间也提高了近3.5 倍.由此我们得知,加入SIMT 算法比单纯的将初值赋为1 效果要好很多.
PERACC(i)代表启发式过程中选择i个变量.从ERACC(2)和PERACC(4)两组数据可以看出:针对比较复杂的问题,PERACC(4)算法已经比较明显地凸显出了其性能的优势.从这两组数据也不难看出:选择变量的数量越多,其求解效率越高.结合表 1 分析,虽然 PERACC 算法在启发式阶段花掉了少许时间,但是整体来看,PERACC(4)比ERACC 效率提高了4 倍~25 倍不等,这也符合了磨刀不误砍柴工的道理.
我们将继续延伸我们的思路,加入了当前国际著名的局部搜索求解器SWCC 进行对比.从数据上不难看出,PERACC 比ERACC 的效率提升了1.6 倍~117 倍不等.虽然PERACC 的求解效率并没有超过SWCC 求解器,但是相对于当前扩展规则领域最高效的ERACC 而言,PERACC 已大大地缩短了与SWCC 的距离.

Table 2 Experiment results on graph Colouring instances flat200-479(CPU time/s)表2 图着色测试用例flat200-479 实验结果(CPU time/s)
我们将实验的证明继续扩大化,选择了AIM 类问题.该类问题结构性很强,变量个数以及正负文字比例存在一定规律,解的个数只有一个,求解难度较高.1_6 和2_0 代表子句与变量的比率,测试用例的变量为100 个.所以,我们将运行1 200s 未结束的测试用例定为Time out.
从表3 可以看出:在前4 个测试用例中,并没有拉开PERACC 和ERACC 的差距,g2wsat 在规定时间内未找到解,SWCC 的数据两极分化比较严重;后4 个测试用例中,仍然体现出了PERACC 的高效性,并且大大地拉开了与g2wsat 的求解差距.虽然在多半用例,我们仍然无法超越SWCC.我们分析:对于结构性较强的AIM 类问题,局部搜索求解结构SAT 问题并不占优势.对于少数测试结果,PERACC 算法超过了SWCC 求解器,这在扩展规则领域是史无前例的,从中也看出扩展规则方法在求解SAT 问题上的巨大潜力.
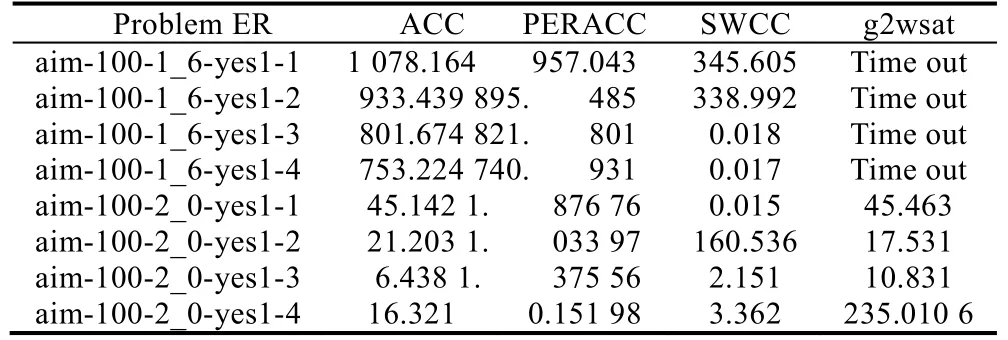
Table 3 Experiment results on AIM instances(CPU time/s)表3 AIM 类问题测试实验结果(CPU time/s)
以上实验结果表明:PERACC 算法在求解复杂性较高、规模较大的测试用例时,更能凸显PERACC 的高效性能,同时缩短了与SWCC 求解器的差距,得到了比较良好的效果.
基于扩展规则的推理方式本身是与归结方法截然相反的求解过程,它是从问题的解空间入手来寻求答案.基于扩展规则的ERACC 算法相比于成熟的局部搜索求解器确有不足,因此,我们在原有基础上做出了一系列改进,进一步研究扩展规则的适用性.我们相信,虽然扩展规则推理方法还处于初级阶段,但与不完备的局部搜索方法相结合,必将发挥出它更大的潜力.
4 总结与展望
本文基于ERACC 算法提出了并行框架,提出了PERACC 算法,我们先后提出了预处理、化简解空间等技术,并行处理各个子空间.通过实验显示:该算法较原算法的求解效率有较大的提高,并不断缩短了与国际著名算法SWCC 的差距.
PERACC 算法在原有算法的基础上进一步大胆地尝试了扩展规则方法领域中不完备推理的发展.下一步,我们决定将DPLL 算法中的单文子传播机制加入其中,从而进一步完善预处理的效果.另一方面,我们将知识约简方法应用于并行前和并行后,通过对复杂问题约简手段的不断提高,才能让我们去不断地求解复杂性更高、规模更大的测试用例.具体的方法还需要进一步进行理论分析和大量的实验来证明想法的可行性,合理与PERACC 结合,使算法的求解能力得到最大化的提升.

