取定s的严格d-正则随机(3,2s)-SAT问题的可满足临界∗
王永平,许道云
1(贵州大学 计算机科学与技术学院,贵州 贵阳 5 50025)
2(贵州财经大学 数统学院,贵州 贵阳 550 025)



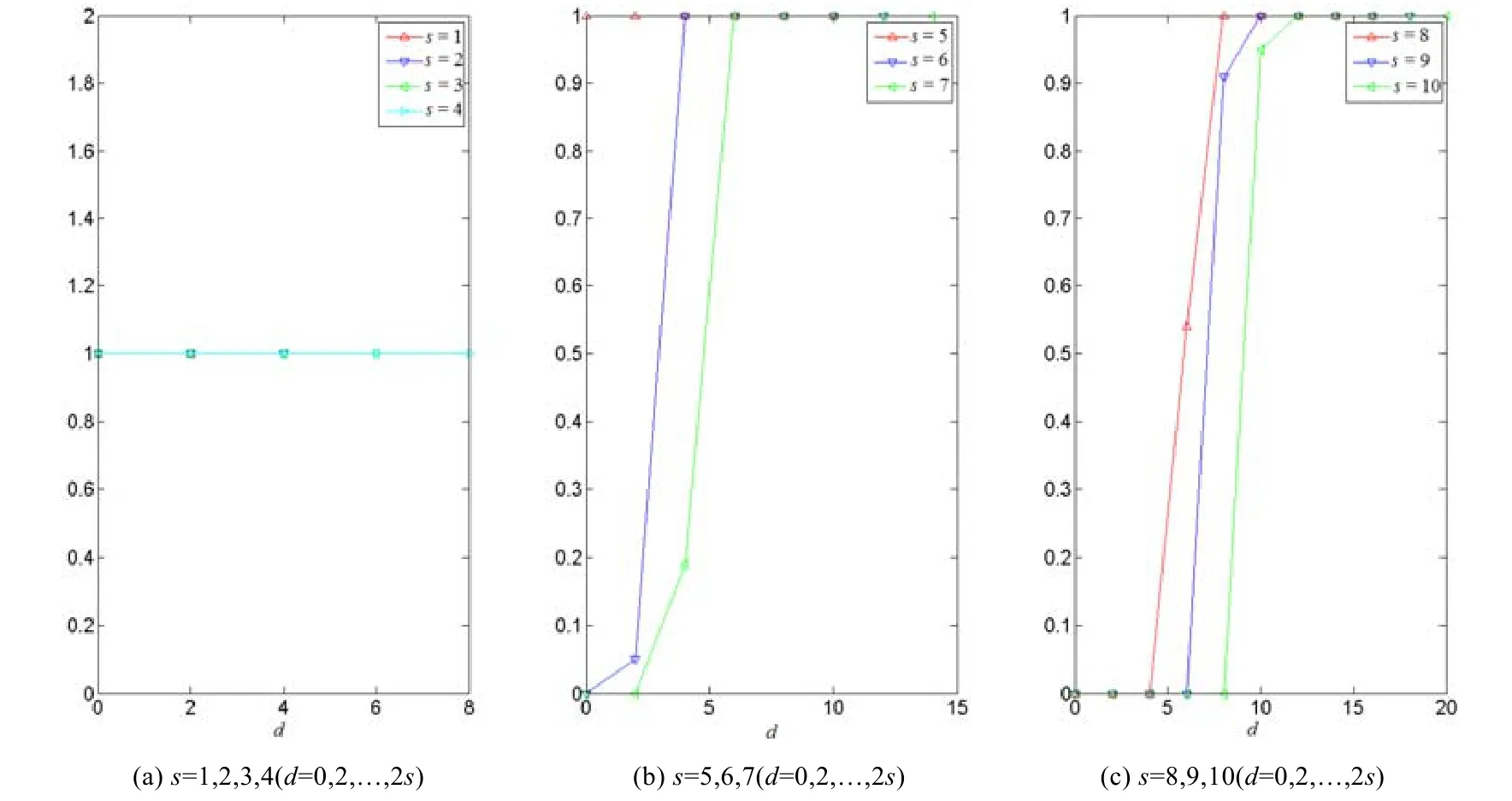
Fig.1 Ratio of satisfiable instances when N=180 and s∈{1,2,…,10}图1 当N=180 而s=1,2,…,10 时的可满足实例占比
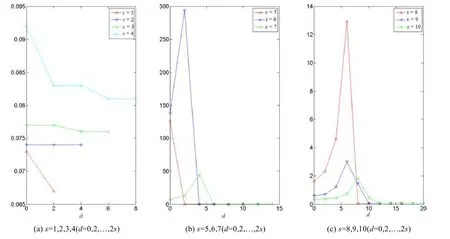
Fig.2 Average time in seconds for solving an instance when N=180 and s∈{1,2,…,10}图2 当N=180 而s=1,2,…,10 时,求解一个实例的平均时间(s)
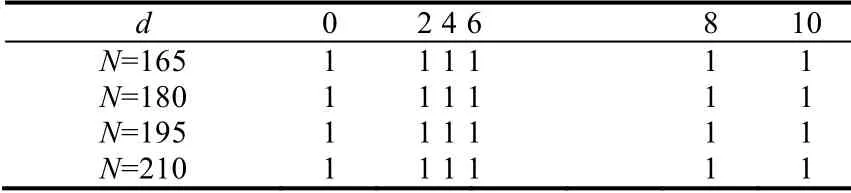
取定整数5 本节主要使用文献[13]的方法研究严格d-正则随机(3,2s)-SAT 问题在s取定时的可满足临界.这一过程主要分成两步:一是通过构造特殊随机实验得到一个特殊真值指派是一个严格d-正则随机(k,2s)-CNF 公式解的概率的渐近表达式;二是使用一阶矩方法得到严格d-正则随机(3,2s)-SAT 问题在s取定时可满足临界值的下界. 设F是一个严格d-正则随机(k,2s)-CNF 公式.如果F的文字全体组成的多重集是L,则由SDRRK2S 模型可知,L可作为该模型Step 2 中的多重集A.由SDRRK2S 模型还可知,该模型可由L生成(2Ns)!个公式.因此,该(2Ns)!个公式中可满足的公式占比即为F是可满足的概率.如果F的文字全体组成的多重集是L′,则由SDRRK2S 模型可知,此时F是可满足的概率与F的文字全体组成的多重集是L时相应的概率相等.因此在本节中,约定F的文字全体组成的多重集是某个取定的集合. 设F是一个严格d-正则随机(k,2s)-CNF 公式.注意到,F是否可满足取决于是否存在作为F解的真值指派.因此,可考虑使用真值指派和公式共同描述该公式可满足的可能性.设l是F的一个文字,σ∈{0,1}N是一个真值指派.如果σ(l)=1,则称l是公式F的由σ决定的1-文字;否则是公式F的由σ决定的0-文字.在不致混淆的情况下,简称l是1-文字或0-文字.设A(F&σ)是1-文字全体组成的多重集,而B(F&σ)是0-文字全体组成的多重集.进一步,设S(F&σ)是SDRRK2S 模型由多重集A(F&σ)∪B(F&σ)生成的公式全体组成的多重集.于是,真值指派σ是公式F解的概率如下: Table 1 Numerial solutions of the null point d0 when s∈{10,20,…,100}表1 当s=10,20,…,100 时,唯一零点d0 的数值解 根据定理3 的条件d Step 1.设k=3,用SDRRK2S 模型生成100 个实例. Step 2.使用Zchaff 求解器[12]分别求解这100 个实例.记求解器成功求解的实例总数是n,并记不可满足实例总数是nu. Step 3.计算nu/n并记之为rs.显然,rs表示在成功求解实例中不可满足实例所占比例. 注意到:当s=30 时,总共需要进行4×12=48 次实验,而且在各次实验中,三元对(s,N,d)互不相同.为方便讨论,记此48 次实验中的任意一个是E.设F是一个严格d-正则随机(3,2s)-CNF 公式,其中,参数s,N以及d恰好是实验E中三元对的各相应值,则实验E的100 个实例可看作对公式F的100 次模拟.进一步,实验E的rs可看作对F是不可满足的概率的模拟.这说明,我们的实验是合理的. 表2~表4 分别给出了s=20,30,40 时的模拟实验结果,其中,11.8310,22.6038,34.3585 分别是s=20,30,40 时d0的数值解.由表2 可知:当s=20 时,对于任取的d<11.8310 和N∈{165,180,195,210},都有rs=1.注意到,rs可看作对公式是不可满足的概率的模拟.因此,表2 支持定理3.同理,表3 和表4 也均支持定理3. Table 2 Va lues of rs when s=20 and d<11.8310表2 当s=20 并且d<11.8310 时的rs 值 Table 3 Va lues of rs when s=30 and d<22.6038表3 当s=30 并且d<22.6038 时的rs 值 Table 4 Va lues of rs when s=40 and d<34.3585表4 当s=40 并且d<34.3585 时的rs 值 此外,同表2~表4 中各个rs均等于1 一样,当s=50,60 时,模拟实验结果也均为rs=1(为节约篇幅,我们没有展示这些结果).因此,s=50,60 时的模拟实验结果也均支持定理3.综上,模拟实验结果验证了理论证明所得下界的正确性. 注意到:在上述模拟实验中,各个rs均等于1.这说明定理3 所得下界仍然比较粗糙,需要进一步改进. 基于严格正则(k,2s)-CNF 公式,我们提出了每个变量正负出现次数之差的绝对值均为d的严格d-正则(k,2s)-CNF 公式.我们使用了新提出的SDRRK2S 模型生成严格d-正则随机(k,2s)-CNF 公式.初步进行的模拟实验表明:当整数5 需要说明的是:从模拟实验结果看,本文所得下界仍然比较粗糙,需要进一步改进.此外,研究讨论该可满足临界值的上界以确定SAT-UNSAT 相变点也十分必要.这些工作将为研究参数d如何影响公式求解难度以及设计随机难解实例生成算法奠定基础.
1 SDRRK2S 模型


2 可满足临界分析
2.1 相关准备
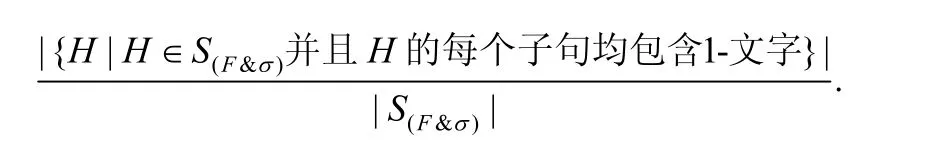




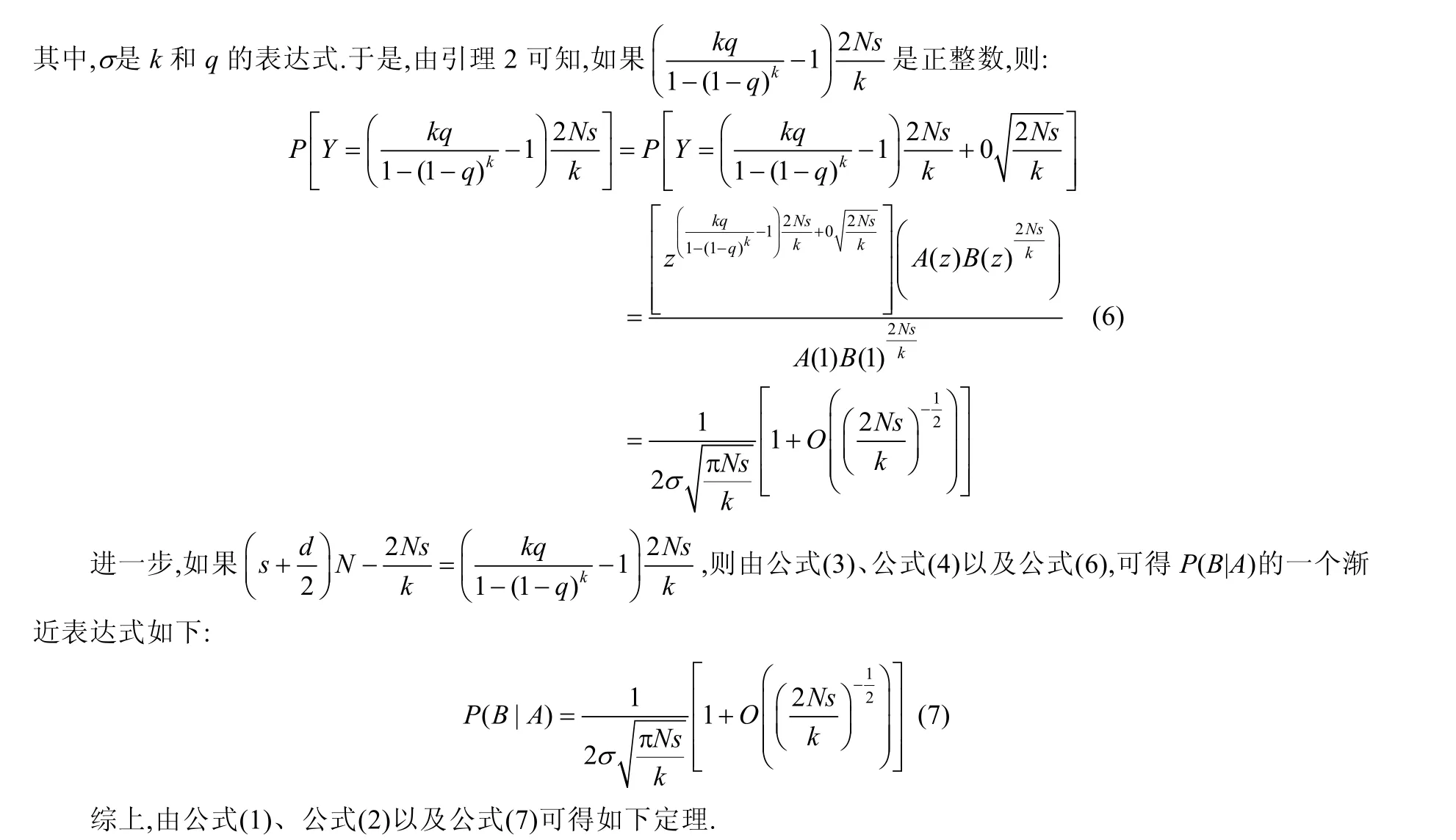


2.2 可满足临界





3 模拟实验


4 结论

