玩出数学课堂中的“数学味”
——浅谈小学数学第一学段模型思想的培养
林晓玉
(集美区后溪中心小学,福建 厦门 361022)
一、科学挖掘教材,积极渗透模型思想
小学数学课程中有许多内容渗透着模型思想,对课程内容的研究是教师进行建模教学的基本前提。首先教师应该要识别并揭示课程内容的知识实质和蕴含的模型思想,在此基础上去挖掘教材中知识的呈现方式。理清课程内容的重点及学生的知识掌握目标,结合学生的认知水平、认知经验及认知方式,积极渗透数学模型思想。
例如,笔者在教学人教版小学数学二年级下册第九单元《推理》时,经历了几次磨课,感受颇多。《推理》是一节数学逻辑推理课,虽说是使学生初步了解逻辑推理的数学思想,但是也蕴含着数学建模的思想。在磨课的过程中,让我深刻地认识到,我们教给孩子的应该是方法,而不是对题讲题,要让孩子学以致用,懂得举一反三。实际上,就是要让孩子在心中有解决问题的思路,脑海中有解决问题的模型思想。这节课在引入部分,让孩子们来猜一猜老师的年龄,我过分强调让孩子们用关联词“不是……,就是……”来描述猜年龄的过程。在新授环节,当遇到三种选择的时候,我又一次强调可以用关联词“不是……也不是……就是……”来进行推理。除此之外,我还将这两个关联词放在板书的重要位置。一堂课下来,我似乎将一节逻辑性很强的数学课上成了语文课,让这节数学课缺失了数学味儿。我的误点是规范孩子推理的表述,而不是教孩子学会解决问题的一连串步骤。经过导师的指导,我才恍然大悟,我们这节课要教会孩子解决这类推理问题的方法步骤。引导孩子从关键的信息入手,最先能确定下来的信息,要先确定下来。接着继续从不能确定的信息入手,把能够排除的可能都排除了,引导孩子有序地推理得出结论。这样子的教学,孩子们才知道遇到这类题型,心中有方法,知道第一步做什么,第二步做什么,有一系列的思路与操作,这样的数学课才有数学味道。这是逻辑推理的过程,这更是数学建模的过程。
二、巧妙运用表格,合理融入模型教学
小学数学中的“解决问题”,其实就是一个主动、生动、充满个性化的建模过程。因此,在引导学生发现数学模型的同时,要主动分析题目中的关键之处,生动个性地运用数学工具来呈现解决问题的过程。借助表格的简洁明了,来帮助分析解决方案,通过对比观察逐步概括成抽象的数学模型,提高学生运用模型思想解决问题的能力。
例如,人教版小学数学三年级上册第三单元《测量》中的运煤问题,载质量分别为2 吨和3 吨的两辆车,如果每次运煤的车都装满,怎样安排能恰好运完8 吨煤?当我们在教学解决这类问题时,孩子们都是直入主题,无序地猜测。首先遇到问题时,要先理清题目中的给定的条件及其限定。引导孩子关注到“每次运煤的车都要装满”,说明2 吨的车每次都要装满2 吨,3 吨的车亦是如此。那么确定好每次车都是装满后,还要关注到关键词“恰好”。“恰好”是刚刚好,不多也不少。所以需要去合理安排,在车子都装满的情况下刚好运完8 吨煤。这节课需要孩子去尝试多种方法解决问题,接着让孩子思考怎样才不会遗漏掉运煤的方案,引发孩子自主地进行有序思考。老师顺势引出表格,利用表格来呈现解决问题的所有方案,凸显列举法的严谨性。虽说要将所有的方案都罗列出来,比较费时,但是这体现了科学严谨的数学学习态度。
紧接着,放手让孩子去列表举例,发现有两种列表方案,一个是从全部安排载质量2 吨的车入手,另一个是从全部安排载质量3 吨的车入手:

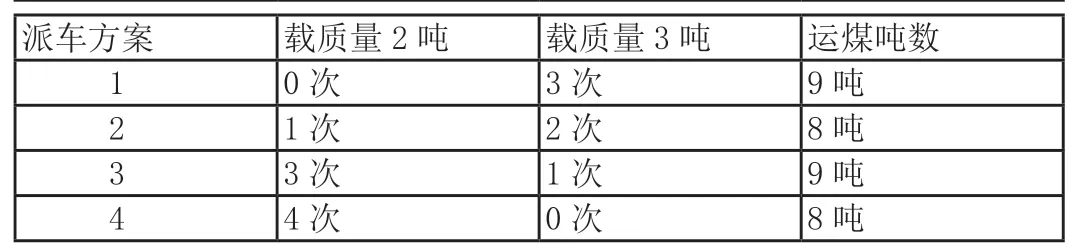
对比观察,发现从载质量3 吨入手,分析的情况会少一些,也更快找到正确答案。通过孩子们的观察和交流,优化出解决问题的方案,列表的时候从较大量入手,这样可以更高效地找到解决方案。在指导学生有序地思考,培养学生的有序思维的过程中,也是构建起解决这类问题的图表模型,提炼出建模背后的蕴含的数学知识。
如此,让学生在数学课堂中经历小组合作及探究,与组员的交流中得出结论,经历一环扣一环的学习过程,引领全班学生共同提炼出模型背后所包含的数学知识,在建构表格模型的过程中,带领学生感悟,把方法学到家,最终适应每一个学生的自身发展,学生可以自由选择自己喜欢的模型来解决问题。
三、精确剖析信息,自主建构模型意识
解决问题中,经常蕴含着大量的文字信息和图片信息,教师应培养学生善于从问题和图片中获取有用的信息,对信息进行精确的剖析。与此同时,还要教会学生合理运用数学图形,将复杂信息转化成简易的数学模型。在学生的认知过程中,要建立一些符号化的数学模型,通过具有“模型”功能的符号、图形等载体,可以帮助学生感悟抽象的数学知识,为今后的数学学习打下坚实的基础。
例如,笔者教学人教版小学数学三年级上册的“归一”问题和“归总”问题时,借助图形、线段图分析数量之间的关系。教学例8时,引导学生从“妈妈买3 个碗用了18 元”入手去思考,可以画碗的简易图,也可以用图形来表示碗。3 个圆形表示碗,再用大括号表示一共有18 元。接着让学生独立画图,求解“如果买8 个同样的碗,需要多少钱”。在解题的过程中,将复杂的文字信息转化成简洁的、直观的图形,学生自然在心中建立了模型图,以后遇到类似的题目可以通过画图来表示,同一幅图也可以代表不同的题目。教学例9 时,对学生抽象概括的能力要求更高一些。不仅仅是学会分析题目的蕴含的关键信息,还需要用到线段图来理解题意。用一段线段表示1 个碗的价格,那买6 个同样的碗,就是要画出6 段等长的线段。那么这整条线段表示的意义,也是学生要在心中建立的模型。这整条线段表示的是买6 个碗的价钱,接下来我们要用同样的价钱去买9 元1 个的碗。因此,我们同样需要用到等长的线段,在等长的线段中取出1 份表示9 元。学生在探究中深刻感受画线段图来整理信息的优越性,意识到图像模型建立的重要性。
四、结语
“授之以鱼不如授之以渔”。教会学生在心中有建模的概念,学会应用模型思想,宛如赋予学生开启数学知识殿堂大门的金钥匙,给了他们“法宝”勇敢闯荡丰富的知识海洋。在第一学段的数学教学中,老师有目的地培养学生数学核心素养——模型思想,在学生的心中搭建起数学学科知识与解决生活实际问题的桥梁。
总而言之,在第一学段的数学教学过程中,教师要注重引导学生在头脑中建立起数学模型的框架,让学生养成一种良好的学习习惯,即尝试运用数学模型思想去解决数学问题。在学习数学的过程中,教师要帮助学生,让他们能够慢慢地提升自身的学科素质,从而培养和提高学生在数学学科的核心素养。学生建立起数学模型思想,是一个十分漫长的过程,需要教师在数学教学过程中,恰当地运用数学工具以及数学手段进行教学,合理运用数学模型的方法,让学生能够自然地将课题上实际的数学问题转化成数学模型,运用数学模型思想,再让学生在课堂上进行反复地尝试和反复地应用,这样学生们才能玩出数学课堂中的“数学味”!

