基于边界域的变精度粗糙集
马周明,王育齐,林依婷
(1.闽南师范大学 数学与统计学院,福建 漳州 363000;2.闽南师范大学 计算机学院,福建 漳州 363000;3.数字福建气象大数据研究所,福建 漳州 363000)
0 引 言
粗糙集理论[1]作为一种处理不精确、不确定、不完备知识和数据的表示、学习、分类方法,在大数据快速发展的今天,已逐渐成为人工智能理论基础方向研究的重要分支。它在机器学习、模式识别、数据挖掘、信息处理、图像处理、医学诊断等诸多领域得到了一些较好的应用[2-9]。
粗糙集理论的核心思想是利用分类方法,将等价关系确定的等价类当作已知的知识集合。进而,利用这些知识来表示任意的对象集。通过一对集值函数:上下近似算子,考虑已知知识包含于对象集,还是至少与对象集相交不空,得到对象集在该已知知识框架下的近似范围。该理论最大的优势在于,不需要通过任何先验知识或主观判断,完全依据数据对任意对象集进行一定知识框架下的刻画。这对知识发现和数据挖据具有非常重要的价值。然而经典粗糙集的这种包含关系,在现实生活中往往太过严苛。从而,随着数据量的激增和类型的日益复杂,严格的包含关系作为粗糙集依赖的描述工具,在一定程度上限制了它在很多复杂环境下的应用和推广。基于此,Ziarko提出了基于一定包含程度的变精度粗糙集模型[10]。其理论的基本思想是在经典粗糙集中给出一个阈值,即允许在一定阈值范围内的错误分类率存在。经典粗糙集就是这种变精度粗糙集阈值为0的特殊情形。因此,变精度粗糙集是经典粗糙集的推广。变精度粗糙集有利于发掘出看似没有关联的数据之间的潜在联系。目前,变精度粗糙集无论在理论研究还是在模型推广方面,都取得较好的发展。比如,双论域情形下的变精度模型及其应用[11],基于覆盖的变精度粗糙集研究[12-13],模糊环境下的变精度粗糙集推广等[14-19]。而且在一些领域得到了比较广泛的应用[20-21]。
变精度粗糙集主要侧重于将经典粗糙集中的严格包含关系放宽为一定程度上的多数包含关系。在数据处理过程中,主要侧重已有知识框架下的知识完整性,这就不可避免地失去了经典近似算子最基本的自反性所对应的公理化特征:对象集的下近似包含于对象集,且对象集包含于其上近似之中。在经典粗糙集的推广研究中,基于其不确定区域,即边界的功能重要性,可直接研究对象集在一定知识分类下的边界区域,从而出现了基于边界域的粗糙集模型[22]。该模型首先考虑对象集的不确定区域,或者边界区域,在此基础上给出相应的上下近似。和经典粗糙集相比,基于边界域的粗糙集从不同的侧面对经典粗糙集进行了阐述。并且和经典粗糙集相比,它具有更良好的性质,比如在一般二元关系下,它总是具有原来自反性和对称性对应的公理化特征。为了进一步探索变精度粗糙集不同情形下的结构和性质,本文研究了基于边界域的变精度粗糙集,给出了3类带有阈值的不同边界域。在此基础上,定义了3类相应的基于边界域的变精度粗糙集模型。分别研究了它们的边界算子以及近似算子的性质。最后,以经典粗糙集作为参照,对最初的变精度粗糙集和这3类基于边界域的变精度粗糙集进行了比较研究。第Ⅰ类变精度模型是已有经典变精度粗糙集模型的推广,第Ⅱ类变精度模型则是经典粗糙集模型的直接推广。这2类变精度模型都侧重于从局部多数包含的角度刻画对象集。第Ⅲ类变精度模型则从对象集的边界域,即整体多数包含的角度描述所研究的对象集合。
1 基于边界域的粗糙集
基于边界域的粗糙集的基本方法,是从优先构造边界集出发,然后给出相关上下近似算子。下面介绍有限论域U中任意对象集X关于二元关系R的边界等相关基本概念。
定义1[22]设R为有限论域U上的任意二元关系,∀X⊆U,其余集记为-X,称
BRL(X)={x∈X|∃y∈-X,xRy∨yRx},
BRH(X)={x∈-X|∃y∈X,xRy∨yRx}
分别为集合X基于二元关系R的下边界集和上边界集。并将
BR(X)=BRL(X)∪BRH(X)
称为集合X基于二元关系R的边界集,简称二元关系边界。显然
BR(X)={x|∃y∈xRy∨yRx,(x∈X∧
y∈-X)∨(x∈-X∧y∈X)}
有了边界集的概念,则称集合
分别为集合X的下近似集和上近似集,X-BR(X)表示集合X与其边界集BR(X)的差集。
定理1基于边界域的粗糙集近似算子和经典近似算子等价的充要条件是论域U上二元关系R是其上的相容关系。
换言之,论域U上的任意二元关系R和其相容闭包的基于边界域的粗糙集近似算子和经典近似算子完全等价。其中,二元关系R的相容闭包是指包含R的最小相容关系(满足自反和对称)。由于经典粗糙集是在等价关系基础上产生的。综上,基于边界域的粗糙集和经典粗糙集在形式上自然是完全等价的。
2 基于边界域的变精度粗糙集Ⅰ
经典粗糙集中的近似算子主要利用了集合的包含关系。对于占绝对大多数的包含或者按照用户需求的一定程度上的包含,经典粗糙集显然无法满足其要求,从而产生了变精度粗糙集,首先介绍下面一些基本的概念。
定义2[23]设U为有限论域,∀X,Y⊆U,称D(Y/X)为集合X在Y中的包含度,如果其满足:
(1)0≤D(Y/X)≤1;
(2)当X⊆Y时,D(Y/X)=1;
(3)当X⊆Y⊆Z时,D(X/Z)≤D(X/Y)。
显然,D(Y/X)=|X∩Y|/|X|是一个包含度。
有了包含度的定义,下面给出基于包含度的变精度粗糙集。
定义3[10]R是有限论域U上的等价关系,D为P(U)上的包含度,α∈(0.5,1],∀X⊆U,记
∪{[x]|D(X/[x])≥α},
∪{[x]|D(X/[x])>1-α}
分别称他们为集合X的α下近似和α上近似。
上面变精度粗糙集的定义,根据给定的阈值α来确定对象集X的上下近似集。显然,它适当放宽了经典近似算子中的包含关系,将其变为某个特定阈值下的多数包含关系,使得这类具有多数包含的粗糙集,在此意义下变成了精确集。下面从边界域的角度出发,考虑变精度粗糙集的基本形式和性质。首先给出下面的定义。
定义4设R是有限论域U上的等价关系,∀X⊆U,称
分别为集合X的α伪下边界和β伪上边界。这里(1>α>β>0)。显然,α伪下边界是包含度相对比较大的等价类之并,而β伪上边界是包含度相对比较小的等价类之并。
尽管约定1>α>β>0,但事实上,为了达到多数包含的现实需要,往往取α为一个非常接近1且小于1的正数,而β则取一个非常接近0且大于0的正数。有了上面定义,称集合


证明(1)—(3)根据定义4显然,下证(4)和(5)。




证明(1)—(4)根据定义4和命题1显然成立。下面证明(5L),(5H)和(6LH)成立。





证毕。
定理2当α+β=1时,基于边界域的第Ⅰ类变精度粗糙集和已有的定义4中的变精度粗糙集完全等价,即对任意的对象集X
证明由上面定义4,下近似相等显然。对于上近似,

{x∈U|D(X/[x])>0}-{x∈U|0 证毕。 通过上面基于边界域的第Ⅰ类变精度粗糙可以更直观地看出,对于任意对象集X,其下近似集不一定包含在对象集X之中。同样,对象集X也不一定包含在其上近似集之中。因此,就经典的变精度粗糙集而言,尽管它将严格包含关系放宽为多数包含关系,但同时也失去了下近似必定包含于所刻画的对象集,以及对象集必包含于其上近似这一重要的性质。 为了尽量让变精度粗糙集中的上下近似算子具有经典粗糙集中的“上”“下”内涵,即下近似包含于对象集,且对象集包含于上近似之中。同样,先给出下面上下边界的定义。 定义5设R是有限论域U上的等价关系,∀X⊆U,称 分别为集合X的第Ⅱ类α下边界和β上边界。这里(1≥α>β≥0)。显然,α下边界是包含度相对比较小的等价类之并,而β上边界是包含度相对比较大的等价类之并。 尽管约定1≥α>β≥0,但事实上,为了达到多数包含的现实需要,往往取α为一个非常接近1且小于1的正数,而β则取一个非常接近0且大于0的正数。有了上面定义,称集合 分别为集合X的第Ⅱ类α下近似集和β上近似集。也称其为基于边界域的第Ⅱ类变精度粗糙集。基于边界域的第Ⅱ类变精度粗糙,直接保证了任何对象集的下近似包含其中,它本身也包含于其上近似之中。下面考虑它们相应的其上、下边界和上、下近似算子的性质。 证明(1)—(6)根据定义5显然.下面证明(7). 证毕。 证明(1)—(4)和(6)根据定义5和命题3显然。下面证明(5L),(5H)和(7LH)。 证毕。 基于边界域的第Ⅱ类变精度粗糙集在适当放宽严格包含的同时,也保留了经典粗糙的一些主要的性质。它主要从每个等价类对于对象集的包含程度进行刻画。然而在经典粗糙集中,也可直接利用对象集的边界(上下边界之并)在对象集中的包含程度进行刻画。先给出一些基本相关概念。 设R为有限论域U上的等价关系,对任意的对象集X⊆U,称D(X)=D(X/BR(X))为对象集X边界包含度。显然,对象集X边界包含度D(X)=|BRL(X)|/|BR(X)|。它也描述了对象集上下边界之间的比例关系,或者是经典粗糙集中上近似集或下近似集接近对象集X的程度。 定义6设R是有限论域U上的等价关系,∀X⊆U,称 分别为集合X的第Ⅲ类α下边界和β上边界。这里(1>α>β>0)。下边界中的“其他”包括D(X)≥α或者BLR(X)=BHR(X)=BR(X)=∅;上边界中的“其他”包括D(X)≤β或者BLR(X)=BHR(X)=BR(X)=∅。 尽管约定1>α>β>0,但事实上,为了达到多数包含的现实需要,往往取α为一个非常接近1且小于1的正数,而β则取一个非常接近0且大于0的正数。这样,上述数学结构才具有更好的现实意义。有了上面定义,称集合 分别为集合X的第Ⅲ类α下近似集和β上近似集。也称其为基于边界域的第Ⅲ类变精度粗糙集。下面考虑其上、下边界和上、下近似算子的性质。 证明(1)—(3)根据定义6显然成立。下面证明(4)—(6)。 证毕。 证明根据定义6和命题5,(1)—(3),(5),(6)显然成立。下面证明单调性(4L),(4H)和α对偶性(7LH)。 证毕。 上述讨论可知,对基于边界域的第Ⅲ类变精度粗糙集,其相应的边界算子不满足单调性。但是其对应的上下近似算子却满足单调性。并且,基于边界域的第Ⅱ类和第Ⅲ类近似算子具有一样的性质。 对于基于边界域的第Ⅰ类变精度粗糙集,根据定理2可知当α+β=1时,它和已有的经典变精度粗糙集完全等价。换言之,基于边界域的第Ⅰ类变精度粗糙集本质上是已有经典变精度粗糙集的推广,且二者表示方式有所不同。经典变精度粗糙集借助包含度,适当放宽包含条件,按照等价类在对象集中的多数包含,给出了其放宽限制的上下近似集;前者依据一定阈值下的包含度,首先给出放宽限制的边界域,或者不确定区域,再利用其给出相应的上下近似集。二者从代数算子的意义上具有完全相同的性质。需要注意的是,经典粗糙集意义上的对象集包含其下近似集,上近似集包含对象集这个重要性质,这2种结构一般都不成立。 下面主要考虑基于边界域的第Ⅰ类和第Ⅱ类粗糙集之间的关系。 定理3对任意X⊆U和满足1>α>β>0的任意α和β,经典粗糙集和基于边界域的第Ⅰ类和第Ⅱ类变精度粗糙集满足下面的关系: 定理4对任意的X⊆U和满足1>α≥β>0的任意α和β,经典粗糙集和基于边界域的第Ⅲ类变精度粗糙集满足下面的关系: 基于边界域的粗糙集首先定义了对象集不确定性地带——边界域,然后直接得到相应的上近似集和下近似集。它和经典近似算子完全等价的充要条件是论域上的二元关系是相容关系。在考虑边界域基本特点的基础上,本文提出3类基于边界域的变精度粗糙集,并详细讨论了它们各自的性质。其中,基于边界域第Ⅰ类变精度粗糙集在阈值满足α+β=1时,和最初的变精度粗糙集完全等价。而第Ⅱ类和第Ⅲ类变精度粗糙集具有比最初的变精度粗糙集更良好的一些性质。结果表明,第Ⅰ类变精度模型是已有经典变精度粗糙集模型的推广,第Ⅱ类变精度模型则是经典粗糙集的直接推广。这2类变精度模型都侧重于从单个知识粒度或等价类在对象集中的包含程度刻画。而第Ⅲ类变精度模型从对象集的整体边界域在对象集中的包含程度进行描述。这些结果在大规模数据处理中,尤其是在无需严格包含或只要求大多数包含的环境中具有一定的实践意义。3 基于边界域的变精度粗糙集Ⅱ






4 基于边界域的变精度粗糙集Ⅲ


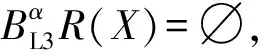
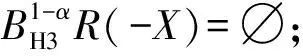



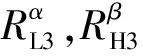


5 几类近似算子之间的关系



6 结束语

