一种高温钢结构计算方法

杨传平，刘 杰，朱永江

(中国五环工程有限公司，湖北 武汉 430223)

高温钢结构广泛存在于工业生产中，例如锅炉支撑、石油化工行业加热炉内部管件支撑、旋转加热炉内部构件支撑等。这些钢结构长期处于高温工况下，且有部分设备钢结构已达到钢材蠕变设计温度(600～900℃)。

目前，国家钢结构设计规范以GB 50017《钢结构设计规范》[1]为主，其他行业性、地方性法规有CECS410：2015《不锈钢结构技术规范》[2]、CECS200—2006《建筑钢结构防火规范》[3]、GB/T 22395—2008《锅炉钢结构设计规范》[4]等。这类结构设计规范中均只适用于设计温度为200℃以下，或者火灾情况下短时间受热钢结构设计，不适用于加热炉内部长期受高温影响的钢结构设计。

SH/T 3036—2012《一般炼油装置用火焰加热炉》[5]中介绍了一种用于计算设计温度为425℃以下碳钢结构的方法，其主要应力计算和评定方法均参照GB 50017，但对常用结构钢材的强度设计值进行了折减，主要考虑高温对于钢材力学性能的影响。此标准虽扩展了钢结构计算方法的温度范围，但仍不能适用于更高温度的钢结构计算。

高温蠕变的钢结构可以采用蠕变材料模型进行有限元屈曲计算，需要考虑蠕变发展过程中第一阶段和第二阶段对屈曲的影响。其中，Norton方程[6]是对材料蠕变第二阶段应力应变关系描述中比较常用的一种，其中一种恒定温度和作用时间下材料蠕变表达式见式(1)。但是此种方法计算量较大，计算耗时较高，不适宜大型钢结构的设计计算。

ε=K′σn

(1)

Flugge[7]提出了一种简便的计算杆件蠕变屈曲载荷的方法，其方程形式和线弹性材料杆件屈曲类似，考虑蠕变的影响，调整了方程中弹性模量值。此方法运用时较为方便，可以很容易地通过查取材料参数获取结果。

本文高温钢结构计算方法参考GB50017，采用以概率理论为基础的状态设计方法[1]，用分项系数设计表达式进行钢结构的强度和刚度校核，其中，材料参数考虑高温影响进行调整；同时采用许用应力法，进行长期高温及蠕变作用下的强度和稳定性校核。

1 高温钢结构的计算方法

1.1 高温钢结构正常使用极限计算

这种极限状态对应于结构或结构构件达到正常使用或耐久性能的某项规定限值。例如，影响结构正常使用的变形、振动，或耐久性的局部损坏[8]。在一般的化工设备中，内部构件载荷以永久载荷为主，本文只考虑永久载荷工况。针对高温钢结构的正常使用极限计算，需要注意的是要使用设计温度下的材料力学性能。

正常使用极限状态设计表达式：

(2)

式中，C为结构或结构构件达到正常使用要求的规定限制，本文主要是位移和挠度限制值；SGik为第i个永久载荷产生的效应值，例如重力产生的位移。

1.2 高温钢结构承载能力极限状态计算

承载能力极限状态对应于结构或结构构件达到最大承载能力或不适于继续承载的变形，例如整个结构或结构的一部分作为刚体失去平衡(如倾覆等)；结构构件或连接因超过材料强度而破坏(包括疲劳破坏)，或因过度变形而不适于继续承载；结构转变为机动体系；结构或结构构件丧失稳定(如压屈等)[8]。同1.1节原因，本文也只考虑永久载荷工况。针对高温钢结构的承载能力极限计算，需要注意的是要使用设计温度下的材料力学性能。

承载能力极限状态设计表达式：

(3)

式中，γ0为结构重要性系数，一般工业建筑取γ0=1；γGi为载荷分项系数，钢构承受载荷主要为永久载荷且起主导作用时取γG=1.35；SGik为永久载荷产生荷载效应值；γR为结构抗力分项系数，碳钢取1.111，不锈钢取1.165；fy为钢材高温下屈服极限标准值。

钢结构强度和稳定性计算时，需要考虑钢结构受力状态分为轴心受力、受弯、拉弯、压弯等，根据材料是不锈钢或者碳钢，其计算公式有所不同，具体见文献[1]和文献[2]。

1.3 高温钢结构蠕变控制

当构件工作温度长期处于材料蠕变温度范围内时，钢材的蠕变将十分明显。当构件应力为拉应力时，结构破坏形式为蠕变失稳破坏，此时使用蠕变许用应力控制即可[9]。

当构件处于压应力状态时，结构可能发生屈曲，或者工作一段时间后，由于杆件蠕变变形后发生蠕变屈曲。此时采用蠕变强度许用应力控制不再合适。按照Flugge[7]介绍的方法，可以很好地解决相关问题。

结构承受恒定应力时，Flugge采用杆件屈曲临界应力如下：

(4)

式中，l为杆件计算长度；r为杆件回转半径；Et为通过材料蠕变等时性曲线取得的切向弹性模量。

联立Et定义、Norton方程式(1)和式(4)，并考虑安全系数FS，可以得到杆件蠕变许用应力：

(5)

设计中取屈曲许用应力安全系数为：

FS=1.5-0.026ln(t)

(6)

式中主要考虑随着时间增加，蠕变变形增加后，非材料因素造成的影响将越来越小，并且在整个构架的设计中，单一杆件因受力较大而产生较大蠕变变形后，其他杆件相应承受更多内力，整体系统内杆件受力呈现均匀趋势。应力集中的杆件破坏的可能性进一步降低。当t=1h，FS=1.5，与GB/T 151-2014中换热管轴向应力失稳安全系数相当；当t=100 000h，FS=1.2。

本文中采用蠕变等时性曲线方法获取切向模量。一般是将蠕变中时间和应变曲线转换为应变应力曲线，由此得到等时性曲线(见图1)。

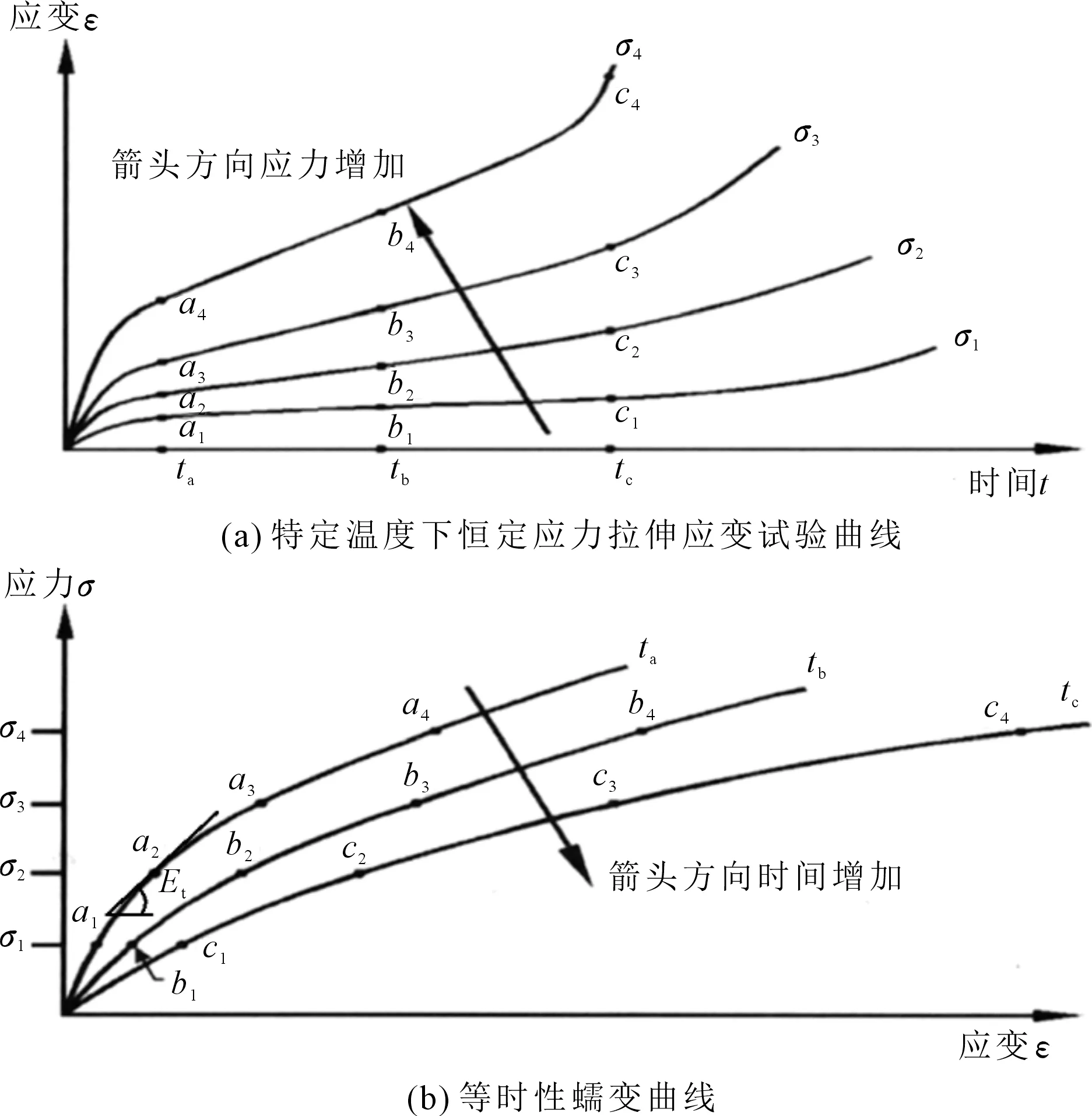
图 1 等时性蠕变曲线转换方法

图1(a)为特定温度下恒定应力拉伸应变试验曲线，将图1(a)中应力应变按图中转换方法转换为图1(b)所示等时性曲线。在满足结构内部应力恒定条件下，采用式(1)模拟蠕变应力应变曲线，从而求出对应恒定加载时间下蠕变应力应变关系中K’和n的取值，从而通过式(5)求得恒定加载时间下的蠕变许用应力。其中，蠕变等时性曲线可通过查询ASME III得到。

由于钢结构中各杆件应力在蠕变作用下趋于平均，因而以蠕变许用压缩应力去限制初始最大压缩用力的方法，总体上是安全且存在一定的保守。

2 算例

某设备内部存在如图2所示高温桁架。其材料为304H不锈钢，设计温度为593℃，设计使用时间为100 000h。304H不锈钢600℃下弹性模量为1.443×105MPa，屈服极限为94.3MPa，泊松比为0.3，平均线膨胀系数为1.794×10-5mm/(mm·℃)。100 000h下拉伸蠕变许用应力为50MPa。结构锥形盘面上承受200mm均匀煤粉重力载荷。304H材料蠕变等时性曲线可以参考ASME III。

图2 某设备内部高温桁架

2.1 高温桁架正常使用极限计算

参照式(2)，按照GB 50017计算方法对结构正常使用极限进行计算，采用有限元计算装置整体位移和杆件挠度。其中，结构最大整体位移和杆件挠度见表1。

表1 结构最大整体位移和杆体挠度

其中，位移值主要作为高温桁架相关支撑和驱动的输入，挠度满足设计要求。

2.2 高温桁架承载能力极限状态计算

参照式(3)，按照GB 50017计算方法对承载能力极限进行计算，验算结构强度和稳定性。利用有限元计算杆件应力，然后参照式(3)，按照GB 50017计算方法分别对强度和稳定性应力进行校核。其中，式(3)右侧fy取593℃下屈服应力值94.3MPa。强度和稳定性应力最大值和允许值见表2。

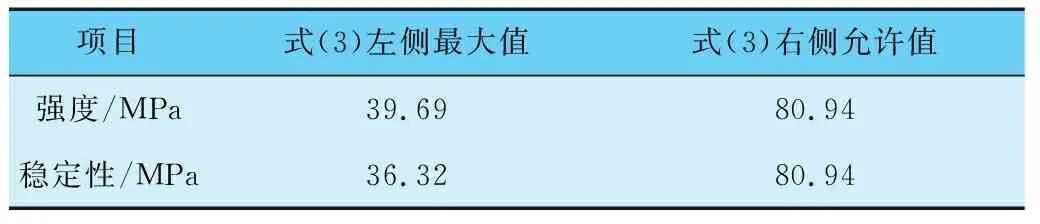
表2 强度和稳定性应力最大值和允许值

根据表中计算结果，高温桁架满足短时强度和稳定性要求。

2.3 高温桁架蠕变校核

(1)桁架结构中应力为拉伸应力状态的，用蠕变断裂强度控制杆件应力。蠕变计算中按照安全系数法进行计算，不考虑载荷分项系数，计算结果见表3。

表3 拉升最大应力和蠕变许用应力

根据表中计算结果可知，高温桁架中拉伸杆件满足蠕变强度控制要求。

(2)桁架结构中应力为压缩应力状态的，用蠕变许用压缩应力控制杆件应力。按照安全系数法计算，结构最大压缩应力为26.9MPa，此杆件的长细比为120。

按照Norton公式拟合，304H材料100 000h下的等时性曲线见图3。

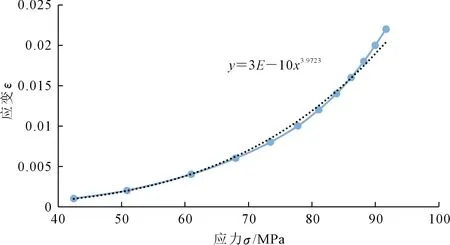
图3 593℃下304H 100 000h 应力应变曲线

从图3中得到参数K′=3E-10，n=3.972 3，根据式(5)计算许用蠕变压缩应力为29.3MPa。由于结构杆件压缩应力小于蠕变许用压缩应力，结构蠕变稳定计算合格。

3 结语

本文提供的高温钢结构计算方法具有如下优点：①考虑了高温对材料性能的影响，且在常温钢结构计算的基础上进行高温修正，具有较强的类比性，易于工程技术人员掌握；②方法考虑蠕变对结构的影响，且控制方法简单清晰，对复杂的蠕变变形采用初始计算结果进行替代，计算结果虽趋于保守，但可较好满足工程需要。