航空三步进分幅图像拼接

岳 广，孙文邦，张星铭，李铜哨

(空军航空大学 航空作战勤务学院，长春 130022)

1 引言

航空遥感目前被广泛应用于种植农业、军事侦察、灾害探测等领域，然而受飞行高度和相机视场角的限制，遥感图像视场较小，能照射到的区域范围有限[1-2]。为了对大目标区域进行全局把握、了解，一般需要多条带或多次成像，然后将多张遥感图像拼接为整幅宽视野图像[3-5]。

当图像条带增加时，给图像拼接也带来了一定难题。随着条带数量增加，图像间的重叠关系增多，图像匹配关系变得复杂。对多条带图像拼接问题的解决方案主要可以分为基于特征匹配的方法和基于POS(position and orientation system)数据的方法。

在基于特征点的拼接方法中，许越等[6]构建了多条带拼接模型，分析了俯仰、翻滚对重叠域的影响，但是该法考虑要素较少，不适用于航空图像。石硕崇等[7]阐述了海洋测绘中的困难，并提出了限制因素，但航空遥感精度达不到测绘水平，适用性不强。在采用机载POS数据进行拼接的方法中，韩文超[8]利用POS数据和特征匹配的方法，完成序列图像拼接，但该法只适用于单条带的图像拼接。徐秋辉[9]通过POS数据结合特征匹配的方法，完成了多条带图像拼接，但实验中未考虑条带间图像的配准关系，拼接效果不佳。Ruizhe Shao[10]提出根据位置和姿态参数，推算下一时刻无人机遥感图像位置，确定条带间图像重叠区域，利用重叠区域中的匹配点对，快速、准确地确定对匹配对位置，该法减少了时间消耗，但对数据精度要求较高。

利用上述方法处理由三步进得到的多条带图像时，发现上述文章大部分都不能较好地解决三并列图像拼接问题，且对多条带图像拼接效果不理想，由于上述方法考虑到的影响因素较少，导致多条带图像拼接出现错位。因此本文针对该问题提出航空三并列图像拼接方法，在保证图像拼接精度的情况下，满足具有三并列分幅图像的拼接。

2 三步进面阵图像几何校正

传统几何校正通常依靠俯仰角、滚转角和偏航角进行坐标转换矩阵解算，利用坐标转换矩阵实现倾斜图像校正为正射图像。然而，当三步进分幅图像需要进行几何校正时，需要考虑到左右倾斜角带来的影响。而且每张图像成像时高度并不相同，校正后所得图像分辨率也不相同，由此给后续拼接带来了困难。为了解决该问题，本文提出结合相机安装角、真航向角、飞行高度和传统校正的3个角元素进行精确几何校正的方法，得到同一地面分辨率的序列图像，为后续的拼接提供了基础。

2.1 传统坐标转换

在几何校正中需要用到计划坐标系O-XLYLZL、像空间坐标系S-xyz、像空间辅助坐标系S-XTYTZT[11]。3个坐标系间关系如图1所示。

计划坐标系记为坐标系A(O-XLYLZL)，计划坐标系的原点在计划拍摄区域内某点上，XL轴沿计划飞行方向，ZL轴垂直于地面向上，且坐标系A构成右手坐标系。

如图1中所示，利用坐标转换矩阵，像空间坐标系转换至像空间辅助坐标系为：

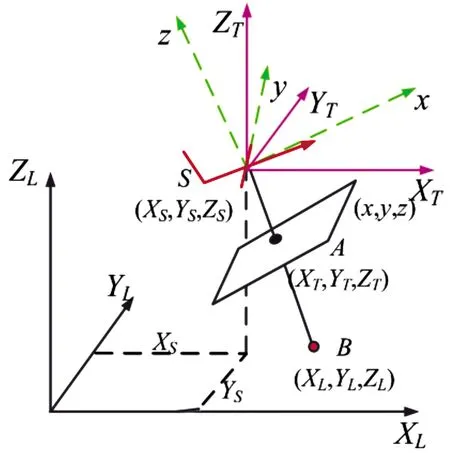
图1 坐标转换关系示意图

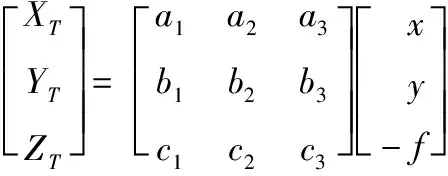
(1)

式(1)中：(x,y,-f)表示像空间坐标系中像点坐标；(XT,YT,ZT)表示像空间辅助坐标系中像点坐标。

构成的坐标转换矩阵为：

(2)

式(2)中，φ，ω和κ分别表示飞机的俯仰角、翻滚角和偏航角。

利用像空间辅助坐标系和像空间坐标系间的转换关系，可以推导像空间坐标系与计划坐标系间关系，即：

(3)

利用以上公式，可以完成像空间坐标系、像辅助坐标系以及计划坐标系三者间的坐标转换。

2.2 坐标系选择与坐标转换改进

2.2.1坐标系选择

本文选择搭载POS系统的无人机机载图像为处理对象。部分POS数据如表1所示，包含数据有飞机飞行姿态信息以及地理坐标信息等。通过分析偏航角与真航向角的变化可以发现，当真航向角发生细微变化时，偏航角未产生变化。由于机载POS系统记录飞行参数时，以一段距离内飞行航迹相对于计划航线的角度记录为当前偏航角，故数据中显示偏航角为0。

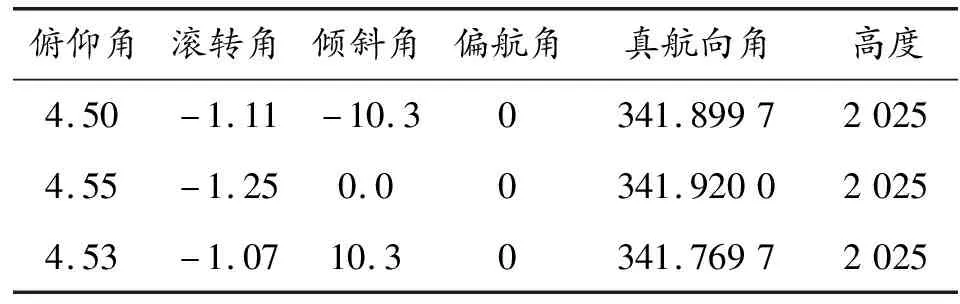
表1 机载POS数据

因此在选择构建坐标转换矩阵时，采用真航向角代替偏航角。确保转换矩阵的精度，并且为了能够与地理信息建立联系，方便后期地理坐标间的嵌套，以真航方向作为参考。为了表述方便，建立了以下坐标系。

1)载机坐标系。载机坐标系C其原点在载机质心，XC轴平行于载机纵轴指向前，YC轴平行于载机横轴指向左，ZC轴平行于载机竖轴指向上。

2)机平坐标系。机平坐标系F其原点在载机的质心，XF轴沿飞机纵轴的水平投影线，且指向飞行方向，ZF轴沿当地垂线指向天顶。

3)机北坐标系。机北坐标系G其原点在载机质心，XG在载机所处位置的当地水平线内，指向正北，YG轴在载机所处位置的当地水平面内，指向正西，ZG平行于当地地理垂线指向天顶。

将图像旋转至航向方向，相应的选择机北坐标系G作为基准坐标系。

为了完成坐标系间的转换，需要重新解算转换矩阵。即需要计算像空间坐标系I→载机坐标系C→机平坐标系F→机北坐标系G之间的转换过程。转换矩阵间计算关系为：

(4)

2.2.2坐标系转换

1)像空间坐标系→载机坐标系转换。

当进行步进分幅成像时，航空相机一般按照一定倾斜角安装在载机上。考虑到相机安装角与载机间的关系，需要计算航空相机坐标与载机坐标间的转角关系，如图2所示。

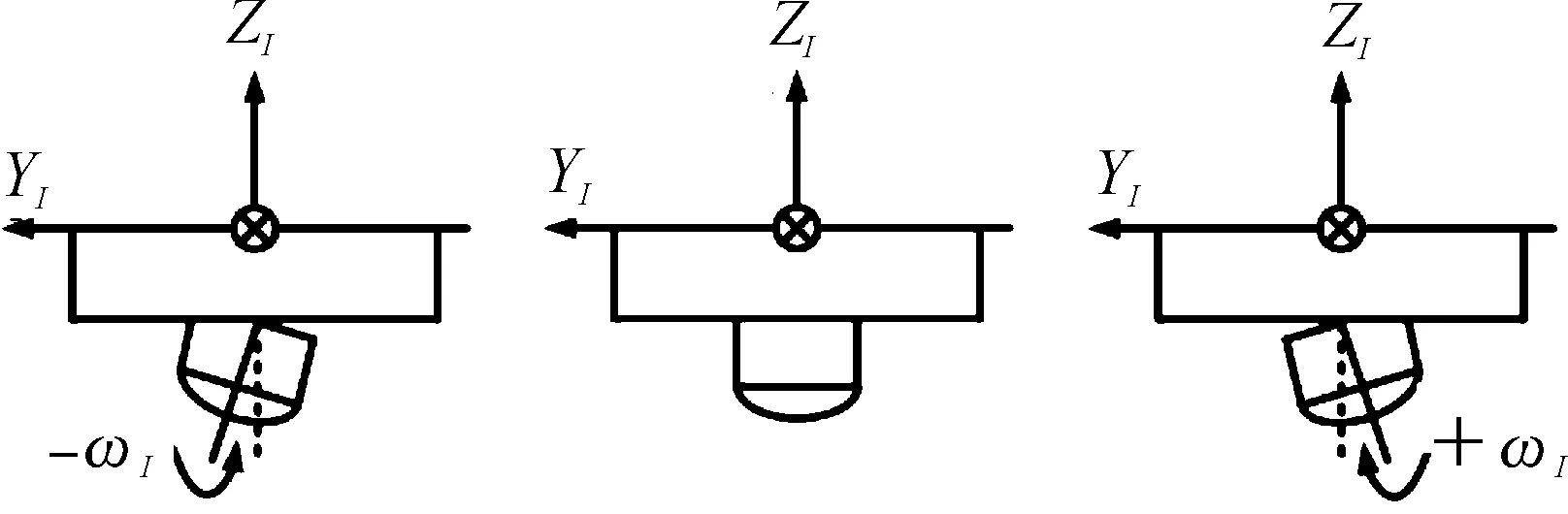
图2 安装倾角示意图

当相机存在左右安装倾角时，一般在摄影测量中规定平台左倾为负，右倾为正。由该安装倾角得到的像空间坐标系→载机坐标系的坐标转换矩阵为：

(5)

2)载机坐标系→机平坐标系转换。

载机在空中由于气流和发动机振动等因素，载机不一定保持平飞状态。因此载机坐标与机平坐标之间存在一定转角关系，包括φ3和ω3等 2个角。由此可以得到载机坐标系→机平坐标系的坐标转换矩阵为：

(6)

3)机平坐标系→机北坐标系。

机平坐标系与机北坐标系只在水平面相差一个航向，而这个航向在相机记录参数中采用真航向来记录。真航向角指飞机纵轴在水平面上投影与当地子午线的夹角。可以得到机平坐标系→机北坐标系的坐标转换矩阵为：

(7)

综上，由像空间坐标系转换至机北坐标系的转换关系为：

(8)

通过解算，可以得到新的坐标转换矩阵为：

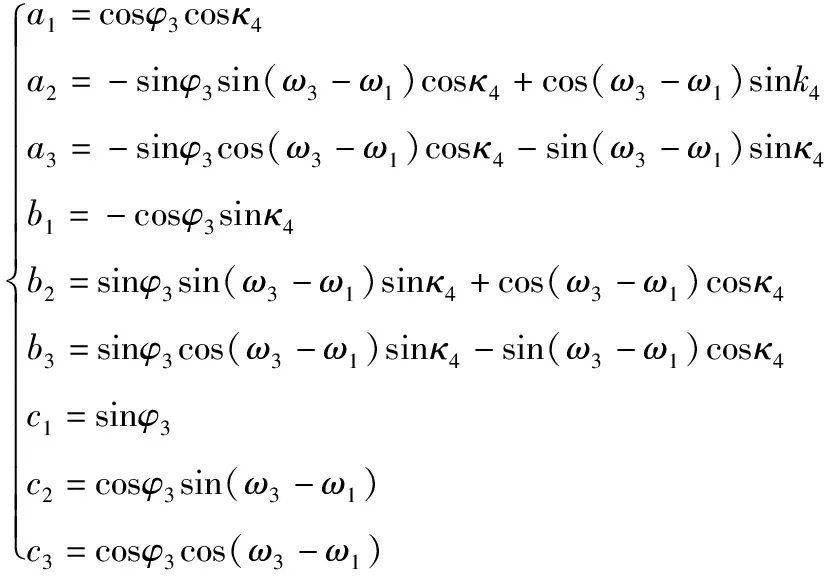
(9)

式(9)中：ω1为相机光轴相对于基座的左右安装角，顺时针转动x轴，即镜头左倾为正；ω3为载机的侧滚角，逆时针转动x轴；φ3为载机的俯仰角，顺时针转动y轴，即上扬为正；κ4为真航向角，顺时针转动z轴，即右转为正。

2.3 改进几何校正算法

利用飞机姿态信息对遥感图像进行几何校正是拼接处理的第一步。仅考虑俯仰角、滚转角和偏航角实现的几何校正，其精度不高且不能满足三步进图像校正。本文提出结合相机安装角、真航向角、飞行高度和传统校正的3个角元素进行精确几何校正。

通过结合相机安装角和真航向角，重新确定了坐标转换矩阵。利用该转换矩阵，可以实现像空间坐标系到机北坐标系的转换。为了得到像点与地面点间关系，利用式(3)推导得到画幅图像构象方程，即：

(10)

式(10)为中心投影构象的基本公式。通过该式建立了像平面坐标系下像点坐标与计划坐标系下的地面点坐标间的联系，也就是说由计划坐标系下地面坐标XA，YA，ZA和摄影中心点坐标XS，YS，ZS可以确定像平面坐标系下的像点坐标x，y。

为了使校正后图像的地面分辨率保持一致，将图像校正过程统一添加高度元素。通过添加高度元素，使得校正图像统一投影至地面，获得了统一地面分辨率的图像。添加高度元素后，式(10)可改进为：

(11)

3 三步进面阵图像拼接

利用POS数据中经纬度信息，可以实现对每张图像拍摄位置坐标的确定，继而可以完成三步进画幅图像粗拼接。由于差分GPS系统获得的经纬度数据精度不高，利用该数据完成的粗拼接有明显的误差，由此进一步进行坐标微调，完成精拼接。

3.1 结合地理信息进行图像拼接

差分GPS系统记录了航空图像拍摄瞬间的位置，表现形式为经纬度坐标。如图3所示，当图像成像时，由差分GPS记录的经纬度坐标为计划坐标系中地底点(D点)位置。地底点为飞机拍摄瞬间摄影中心S正下方且位于地平面上的点。为了完成结合地理信息的图像粗拼接，需要通过寻找图像中像底点与地面地底点位置坐标，在统一的地面分辨率下，将两点信息进行嵌套，即可完成拼接。

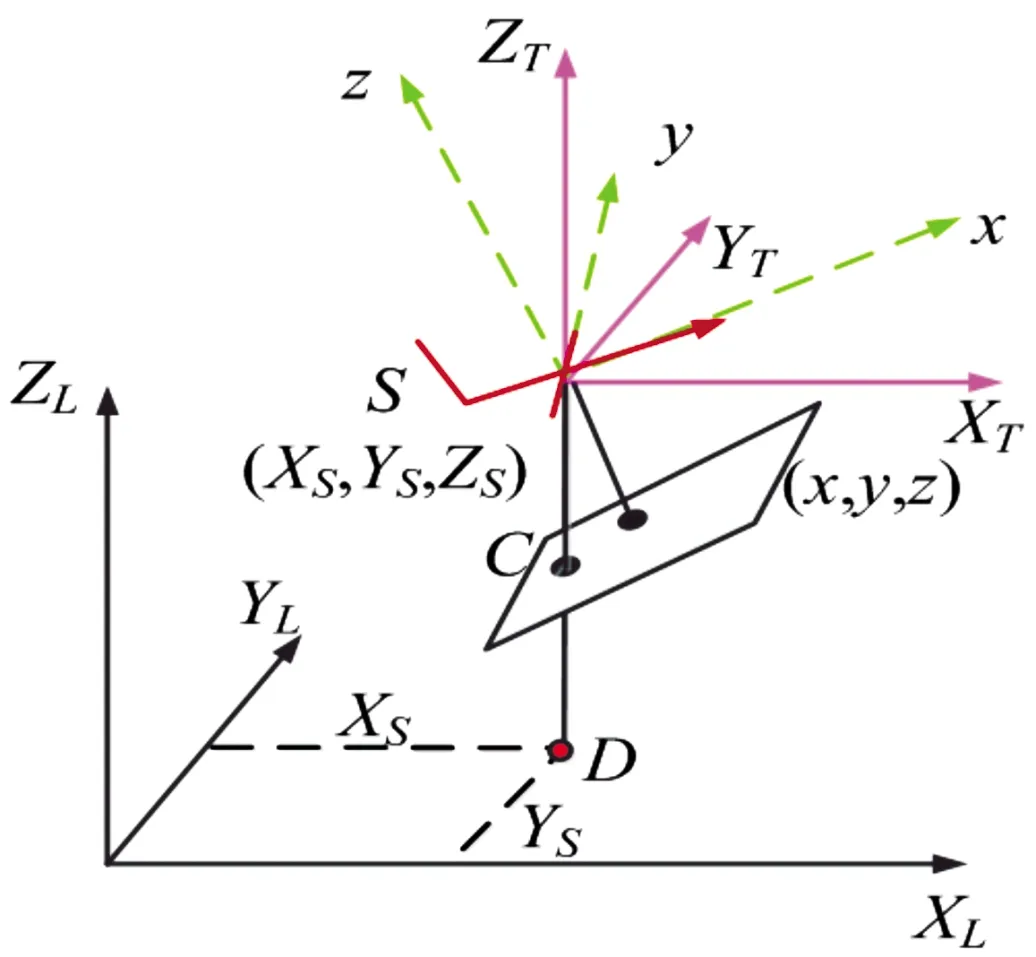
图3 像底点与地底点位置示意图

3.1.1像底点坐标确定

图3中C点为像底点。像底点是过摄影中心S作地平面的垂线与像平面的交点。像底点位于像平面内，表现形式为像点坐标。经几何校正后像底点坐标发生了变化，为了确定像底点坐标的位置，需要在校正后图像中寻找。

如图4所示，图像中展示了几何校正后的图像与坐标系统间的关系。

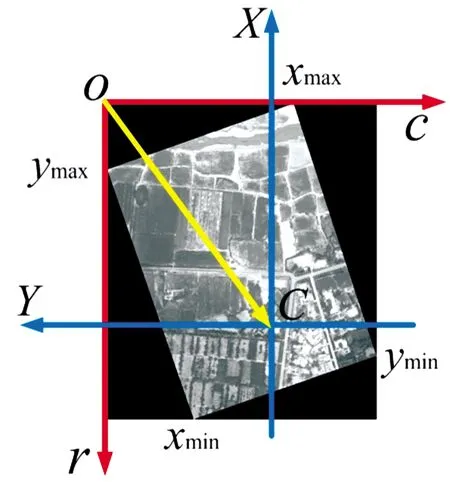
图4 寻找像底点示意图

图4中，O-cr为数字图像显示坐标系统。C-XY为数字图像运算坐标系统，由于在几何校正过程将图像方向旋转至真航向方向，因此X轴指向真北方向，Y轴垂直于X轴向右。图4中C表示为像底点，完成图像几何校正，记录图像4个顶点坐标，通过观察图4可以发现，O点相对于数字图像运算坐标系的坐标等同于C点相对于数字图像显示的坐标。通过记录每张图像的边缘max点，即可求得像底点坐标。

然而当成像模式为三步进时，左右相机安装倾角的大小将会影响像底点是否存在图像上。如图5所示，当相机安装倾角过大时，像底点存在于像平面内而不在图像上。

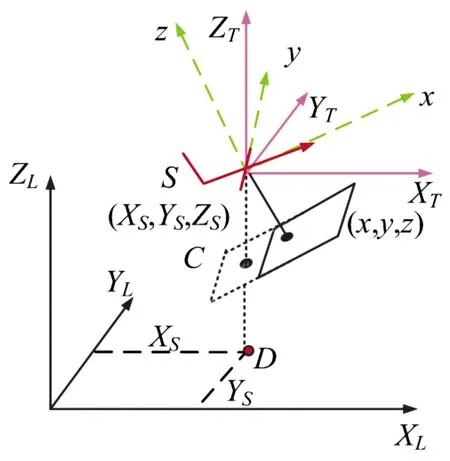
图5 安装倾角示意图

在这种情况下，几何校正后的图像与坐标系统间的关系如图6所示。像底点C坐标求解与上述方法一致。然而在构建数字图像显示坐标系统时需要考虑C点坐标是否存在于图像上。当C点不在图像上时，需要构建新图像将C点包含在内并对该坐标进行相应记录，以便后期使用该点坐标。

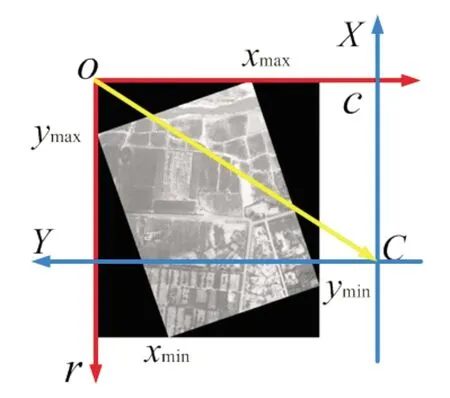
图6 像底点不在图像上示意图

3.1.2地底点位置坐标确定

图3中D点为地底点。由POS系统记录当前地底点的表现形式为经纬度坐标。在图像拼接中，计算图像与图像间的距离及方向信息，即可确定图像位置。

通过POS系统记录的经纬度坐标，确定各点间的位置关系。各经纬度间弧长计算如下：

(12)

SB=ΔLN0cosB0

(13)

式(12)～(13)中：ΔB=B-B0；Mm为Bm处的子午线曲率半径；Bm为B和B0的平均纬度；e′为椭球第二偏心率；ΔL=L-L0；N0表示卯酉圈曲率半径。

通过式(12)，可以计算子午线上各纬度间弧长，当子午线很短时，如子午线两端纬差ΔB<20′，精确到0.001 m，可将子午线视为圆弧，其曲率半径采用两端平均纬度处子午圈曲率半径。同理，通过式(13)，可以计算平行圈上经度间弧长。

利用上述所求得的经纬度差对应的弧长距离，计算欧式距离作为两地底点间相对距离。当航向方向确定时，两地底点间的相对方向也确定。由此，基于经纬度信息可以计算出各地底点间的位置及距离关系。

将寻找到的像底点坐标与对应的地底点坐标进行嵌套，即可完成基于地理信息的图像拼接。

3.2 结合特征匹配进行坐标微调

仅利用位置坐标进行图像拼接时，对POS系统记录数据精度要求很高。在处理POS系统精度不高的图像数据时，仍需要进一步进行精拼接。

利用特征匹配可以解决上述问题。通过在图像重叠区域间进行特征检测并匹配，剔除误匹配对后，根据三步进图像成像的特点，选择坐标微调策略，将匹配正确的特征点用于坐标微调，以纠正POS数据带来的误差。

3.2.1特征检测与匹配

SIFT特征点对图像平移、旋转、缩放具有不变性，对光线变化、噪声、仿射变化有着较强的鲁棒性[12-14]。因为SIFT特征点比较明显，所以依据这些点辨别图像准确率较高。为提高SIFT算法运算效率，需要在重叠区域内提取特征点。完成特征检测后，将特征点进行特征匹配，剔除误匹配对。

3.2.2利用匹配对进行坐标微调

剔除误匹配对后，记录下当前状态下各特征点位置坐标。通过像底点与地底点的嵌套，使得图像中特征点坐标一同嵌套至地面点坐标，并记录为新图像下的坐标。如图7所示。(rml1,cml1)与(rl1,cl1)分别为中央条带和左侧条带相应匹配点的坐标，(rmr1,cmr1)与(rr1,cr1)分别为中央条带和右侧条带相应匹配点的坐标。为了减少误差累积的效果，选择中央条带图像作为基准图像，通过式(14)计算左、右图像与中间图像间距离，得到了需要微调的坐标值。

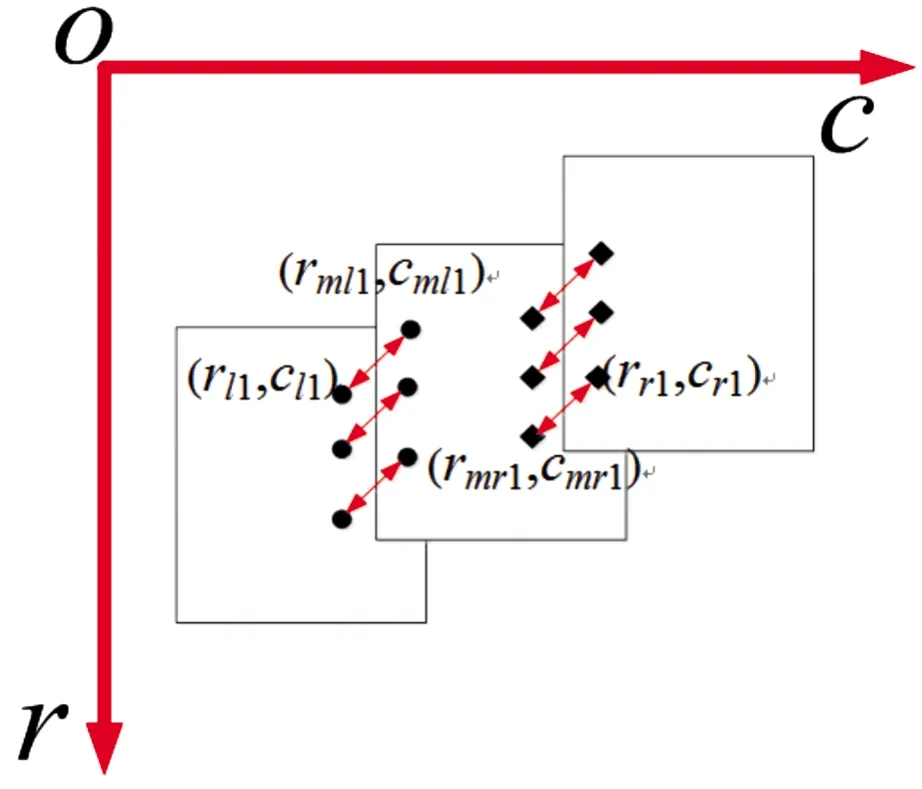
图7 坐标匹配示意图

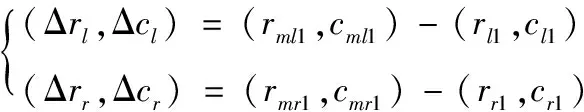
(14)

式(14)中：(Δrl，Δcl)表示中央条带特征匹配点与左侧条带特征匹配点的距离；(Δrr，Δcr)表示中央条带特征匹配点与右侧条带特征匹配点的距离。

由于特征匹配对并不唯一，经计算得到的微调值并非为单一值。为了保证微调值的精准度，将以上求得的若干个微调值进行筛选，在一定阈值范围内计算各微调值的累积频率，取累积频率最大值对应的微调值作为最终微调值。实验中阈值设为10。

如图8所示，通过左右图像与中央条带进行坐标微调，即可完成单个周期内图像坐标微调。重复上述步骤，即可完成多个周期条带间的坐标微调。

图8 坐标微调策略示意图

完成周期图像坐标微调后，然后进行条带间图像坐标微调。虽然条带间三幅图像均具有重叠率，且各张图像特征匹配关系不尽相同，但在进行周期微调时，选择了中央条带作为了基准图像。因此，在进行条带间图像微调时，为了使得误差累积效果减少，以中间周期图像为基准图像，使得上下两侧周期图像进行微调，由此完成了图像精拼接。

4 实验与分析

本文实验采用无人机拍摄某地区的I1～I9图像，如图9所示。此次航空拍摄采取三步进分幅成像模式，图像尺寸为5 344像素*4 008像素，航向重叠率为20%，横向重叠率为10%，对应每张图像的机载POS数据主要参数如表2所示。实验硬件条件为 Inter(R)Core(TM)i5-10210U CPU@ 1.60 GHz，内存为8 GB，软件条件为Matlab 2016b。

图9 实验图像

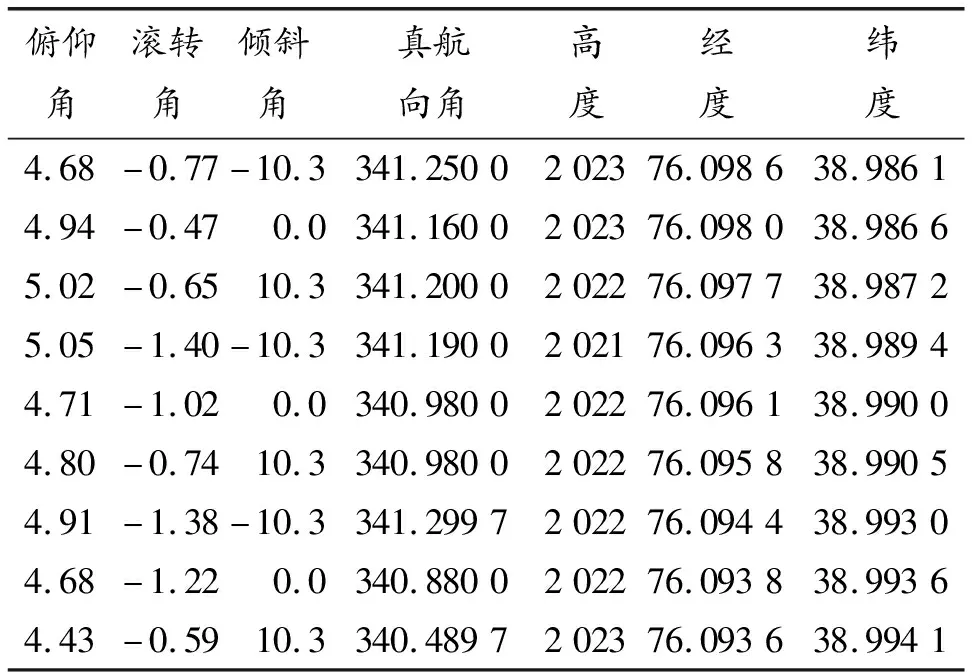
表2 实验图像POS数据主要参数

利用飞机姿态信息，通过式(11)，完成图像几何校正，获取了统一分辨率下的正射图像。几何校正图像如图10所示。实验中分辨率设为0.1 m。

图10 几何校正图像

通过式(12)和式(13)计算地面上机下点间相对距离，将各点间相对位置标定，绘制飞行航迹，如图11所示。在绘制飞行航迹时，将地面航迹路线图分辨率与几何校正后图像分辨率保持一致，以保证后续图像间的正确嵌套。

图11 飞行航迹图

图11中直线表示大致飞行航迹，白色三角表示每张图像拍摄时对应的地面位置。按照飞行方向判断，从右下角到左上角依次为拍摄第1张至第9张时对应地面位置。根据图6所示方法，在校正图像中记录下像底点坐标，如图12所示，图12中白色圆点表示像底点坐标。由于采用三并列成像方式，左右安装倾角较大，故像底点坐标没有落在图像上。

图12 像底点位置图像

将图12中像底点坐标与图11中相应的航迹点嵌套，在图11中绘制基于地理位置坐标拼接的图像，拼接结果如图13所示。在图13中，各幅图像的大致位置基本确定，但由于数据精度较低，导致拼接中存在大量错位现象。在道路、建筑明显目标区，错位现象明显，视觉效果差，因此需要进行进一步精拼接。

图13 基于地理位置坐标拼接图像

利用SIFT算法提取特征点并进行特征匹配，经剔除误匹配对后，记录各匹配对的位置坐标。利用匹配对间的坐标关系，通过式(14)计算得到各图像间坐标微调值。采用先微调周期图像，后微调条带图像的顺序，得到精拼接图像，如图14所示。

图14 精拼接图像

通过对比细节部分，如图15所示，发现经坐标微调后，图像间无明显拼接错位现象，道路、建筑物等明显目标无明显变形。精拼接效果明显优于粗拼接，视觉效果较好。

图15 对比坐标微调前后的图像

5 结论

提出了改进几何校正和三步进图像拼接的新方法。实验表明，本文算法实现了对三步进图像的无缝拼接，解决了传统算法对三步进图像拼接难以处理的问题，对比依靠地理位置信息拼接的图像，具有更好的拼接效果。