一种星敏感器/陀螺组合卫星姿态确定算法

周竹青，李星秀，吴盘龙

(南京理工大学 a.自动化学院；b.理学院，南京 210094)

1 引言

遥感卫星是观测地表覆盖和自然现象的一个重要手段，随着对地观测技术的发展，在无地面控制条件下，卫星遥感对地观测定位精度要求越来越高。高精度的姿态信息是测绘卫星高精度定位，特别是无地面控制下定位的重要前提[1-2]。高精度测绘卫星的自主定姿可以采用星敏感器/陀螺组合定姿方案，因为陀螺能够连续输出角速度，实时性好，但是陀螺存在漂移；而星敏感器可以获得高精度的姿态信息，但是它的工作频率较低。星敏感器/陀螺组合定姿方案用星敏感器获得的高精度的姿态信息来补偿陀螺漂移量，实现互补，获得高精度的卫星姿态[3]，为测绘卫星定位精度的提高打下基础。

姿态确定方法分为两类，一类是确定性方法，另一类是状态估计方法。确定性方法就是根据一组矢量观测值求出卫星的姿态，有TRIAD、q-方法、QUEST法等，其中QUEST算法与其他算法相比，兼具鲁棒性和快速性[4-6]。确定性方法结构简单清晰，但是无法考虑测量过程和模型中的各种误差，而且只能处理星敏感器这类输出观测矢量敏感器输出的数据，无法处理陀螺数据。状态估计算法就是通过建立状态量的状态方程和测量方程，应用估计算法，根据观测量估计出状态量，估计算法有扩展卡尔曼滤波(EKF)、无迹卡尔曼滤波、容积卡尔曼滤波等[7-9]。非线性滤波算法可以抑制观测误差对定姿精度的影响。然而姿态估计算法精度非常依赖系统模型的建立，并且有稳定性不好，易发散等问题。

为使上述两类姿态确定算法实现优势互补，本文提出一种基于改进QUEST算法的两步最优估计算法，将确定性算法QUEST和估计算法EKF相结合。不仅可以利用QUEST算法处理星敏感器数据，降低姿态确定系统的非线性程度，还可以利用EKF估计出星敏感器的测量误差和陀螺漂移。并且因为QUEST算法无法判断姿态四元数的正负，导致输出的四元数不连续，这里对QUEST算法进行了改进。

2 陀螺及星敏感器测量模型

陀螺量测方程为

ωg=ω+d+ηg

(1)

式(1)中，ωg为陀螺的输出，d为陀螺漂移，ηg为陀螺的测量噪声，一般视为高斯白噪声。陀螺的漂移d满足：

(2)

式(2)中，ηd为高斯白噪声。

星敏感器测量得到的是恒星的方向矢量，采用准直型探测器孔径成像或者调制型编码成像技术。假设卫星上的安装的探测器系统由镜筒和CCD阵列敏感器器件组成，定义探测器平面的中心点为测量坐标系的原点Om；OmZm轴指向脉冲星方向，为探测器中心主轴；OmXm轴垂直于OmZm轴，指向CCD行扫描方向；OmYm轴与另外两轴构成右手坐标系Omxmymzm，如图1所示。

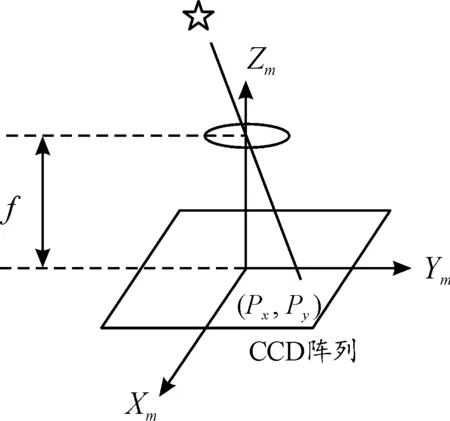
图1 星光成像几何关系示意图

恒星在星敏感器测量坐标系下的单位星光矢量m为

(3)

式(3)中，f为镜筒焦距，(px，py)为星光矢量在CCD阵面上的坐标。

由于卫星星体坐标系到星敏感器坐标系的安装矩阵已知，设为Cbm，所以可以得到恒星在星体坐标系下的单位星光矢量b为

b=Cbmm

恒星在惯性坐标系下的单位参考矢量r为

(4)

式(4)中，α、δ为恒星的赤经、赤纬。

b、r之间的关系如下：

b=Cbir+ε

(5)

式(5)中，Cbi是卫星本体坐标系当对于惯性坐标系的转换矩阵，ε为星敏感器的测量误差。

3 星敏感器/陀螺组合的卫星姿态确定算法

姿态确定算法原理如图2所示，将星敏感器测得的矢量信息经过QUEST算法预处理后得到的卫星姿态四元数，与陀螺状态更新后所得的姿态四元数，作四元数差得到的误差四元数，以此作为 EKF的量测值。

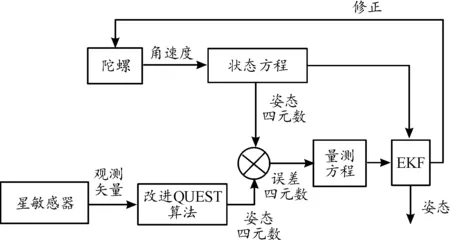
图2 卫星姿态确定原理

3.1 改进的QUEST算法

由1.2节可知星敏感器是通过测量得到恒星在星体坐标系下的星光矢量来求取姿态的。Wahba将这类基于矢量观测求解卫星姿态的问题描述为在最小二乘意义下,求解最优正交姿态矩阵的问题，即求解使Wahba损失函数

(6)

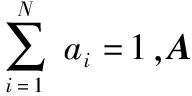
定义增益函数g(A)：

g(A)=1-L(A)=tr[ABT]

(7)

式(7)中，tr代表的是矩阵的迹，矩阵B为

那么求解卫星姿态问题就转化为求解使g(A)最大的正交矩阵。Davenport引入四元数q[10]：

(8)

g(q)=qTKq

(9)

式(9)中，K是4×4维矩阵：

那么求解出使得g(q)最大的四元数q即求得卫星的姿态。经证明满足条件的最优四元数即为矩阵K最大特征值所对应的特征向量，即：

Kqopt=λmaxqopt

然而，因为q和-q都是K的最优特征向量，即：

K(-q)=λmax(-q)

无法判定四元数的正负，即不能得到一个连续的四元数输出，也没有办法使用误差四元数进行工程上的其他应用。为了解决这种问题，根据幂法求解特征向量的原理[11]。如果K的最大特征值是唯一的，并且有最大的绝对值，那么它可以写成

(10)

式(10)中，p为模为1的随机四维列向量。对式(10)进行离散化，可得:

(11)

式(11)中，k=1,2,3,…，初始四元数q0=p也是一个随机向量，对于标准正交的A，可以写出K的特征分解：

K=VDV-1

(12)

式(12)中，D=diag(λ1,λ2,λ3,λ4)，且λ1≤λ2≤λ3≤λ4，V是按顺序属于所有特征值的特征向量组成。根据Mortari的文献[12]可以得到-1<λ1≤λ2≤λ3<λ4≈1，那么：

Vdiag(0,0,0,1)V-1=qqT

最终的连续解表示为

qk=qqTqk-1,qk=qk/|qk|

即：

qk=sign(qTqk-1)q

(13)

式(13)中，sign(·)表示取符号。这里的qk是最优四元数的标量，这表明连输四元数在Wahba最小二乘的意义上是最优的，但对于四元数的选择是连续的。

3.2 系统状态模型

基于星敏感器/陀螺的卫星姿态确定系统的主要思路是用星敏感器得到的高精度的姿态信息来补偿陀螺的漂移。这里用四元数来描述卫星姿态，四元数姿态动力学方程为

(14)

定义误差四元数和误差角速度：

(15)

(16)

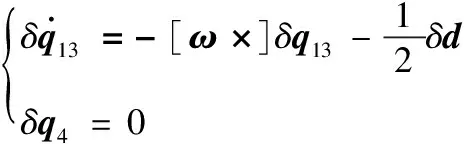
取系统状态量δX=[δq13,δd]T，那么系统状态方程为

(17)

将状态方程进行离散化处理，可以得到离散状态方程：

δXk=Φk-1δXk-1+Gk-1Wk-1

(18)

式(18)中，Φk-1=1+F(t-1)T，T为采样时间。

3.3 系统量测模型

星敏感器的输出为观测星在卫星星体坐标系的方向矢量。QUEST算法要求至少要得到2个不同的观测星在卫星星体坐标系的方向矢量，本文假设在星敏感器视野内有至少两颗可观测星。本文利用2个观测星测得方向矢量，通过改进QUEST算法计算得到卫星四元数。本文的观测量为星敏感器的测量残差，定义量测量：

(19)

式(19)中，qpre根据式(14)预测得到，qstar为利用星敏感器的测量数据计算得到姿态四元数，根据式(13)计算得到。因为量测数据是离散的，所以系统的量测方程为

δZk=HkδXk+Vk

(20)

3.4 算法流程

根据状态方程式(18)和量测方程式(20)，使用EKF进行卫星姿态确定的流程如下：利用k-1时刻的状态量得到k时刻的状态量过程如下：

1)根据k时刻星敏感器的测量值，利用改进的QUEST算法，计算得到k时刻的量测四元数(qstar)k。

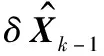
3)根据式(20)计算量测误差量δZk，进行状态更新：

其中，Rk为系统量测噪声矩阵。

4 仿真试验及结果分析

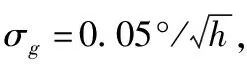
由图3和图4对比可知，由于星敏感器测量精度很高，QUEST算法可以求得高精度姿态四元数，但是它无法判断四元数的正负，就出现了图4所示的情况，与真实姿态四元数符号相反和输出不连续的问题。而经过改进之后如图3所示，可以准确判断姿态四元数的正负，输出连续的四元数。

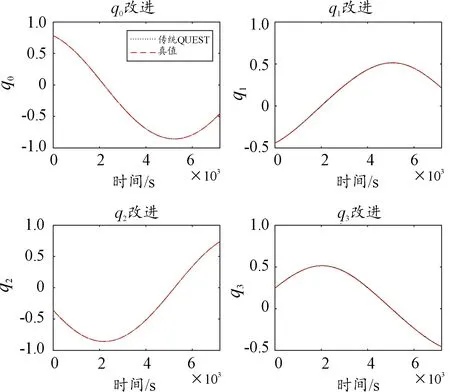
图3 改进QUEST算法求得姿态四元数与真值曲线

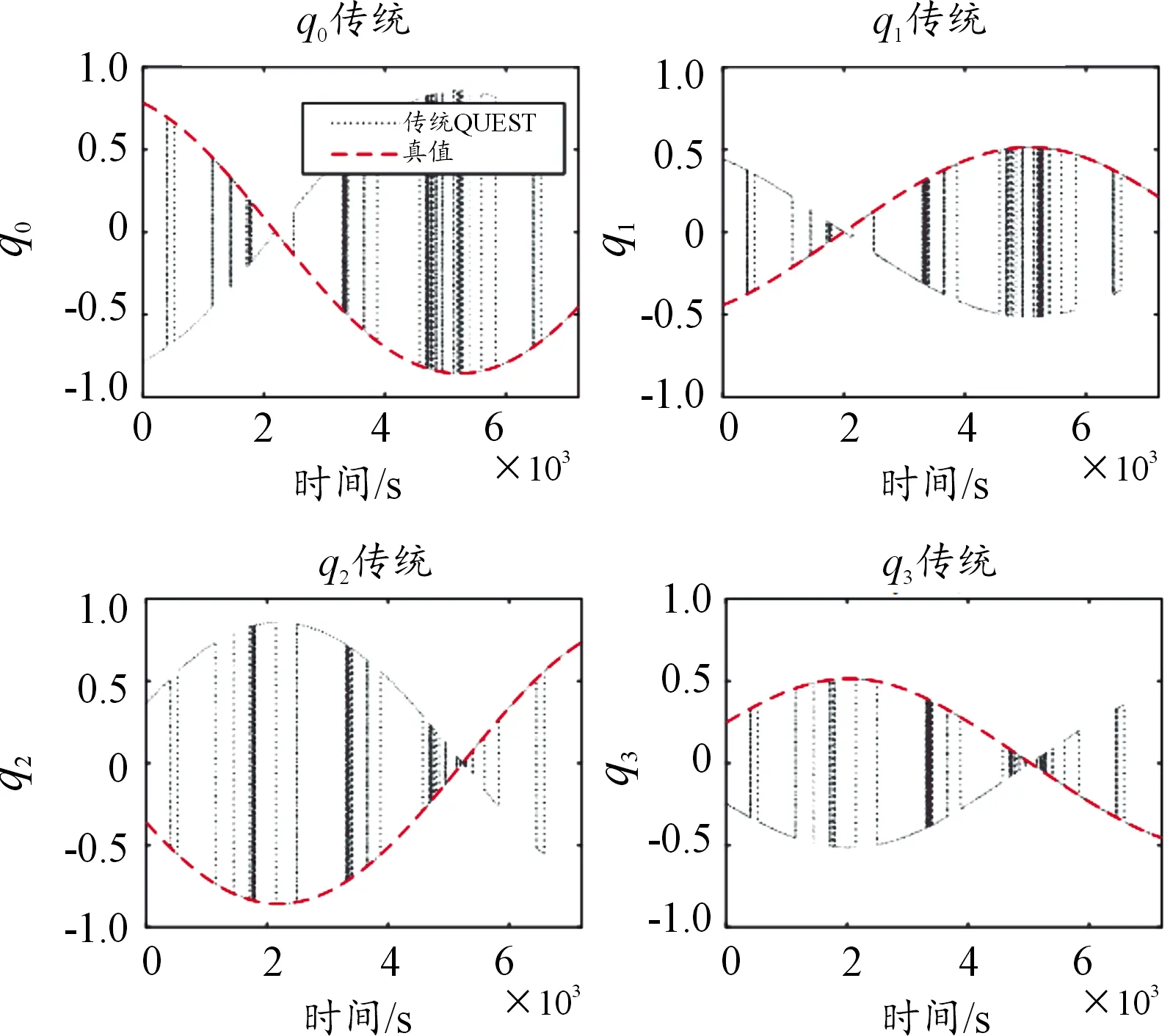
图4 QUEST算法求得姿态四元数与真值曲线

基于星敏感器/陀螺的卫星定姿仿真结果如图5、图6所示。其中红色曲线表示从4 000 s开始出现1 min陀螺仪数据丢失情况时的仿真结果。

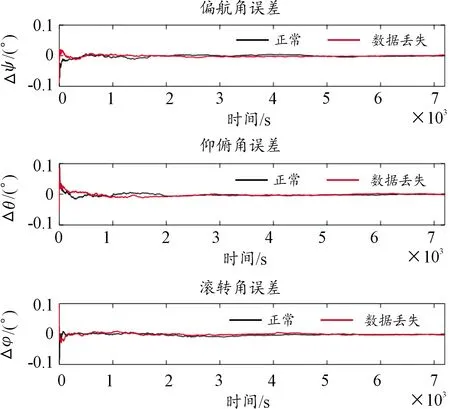
图5 基于星敏感器/陀螺的卫星姿态误差曲线

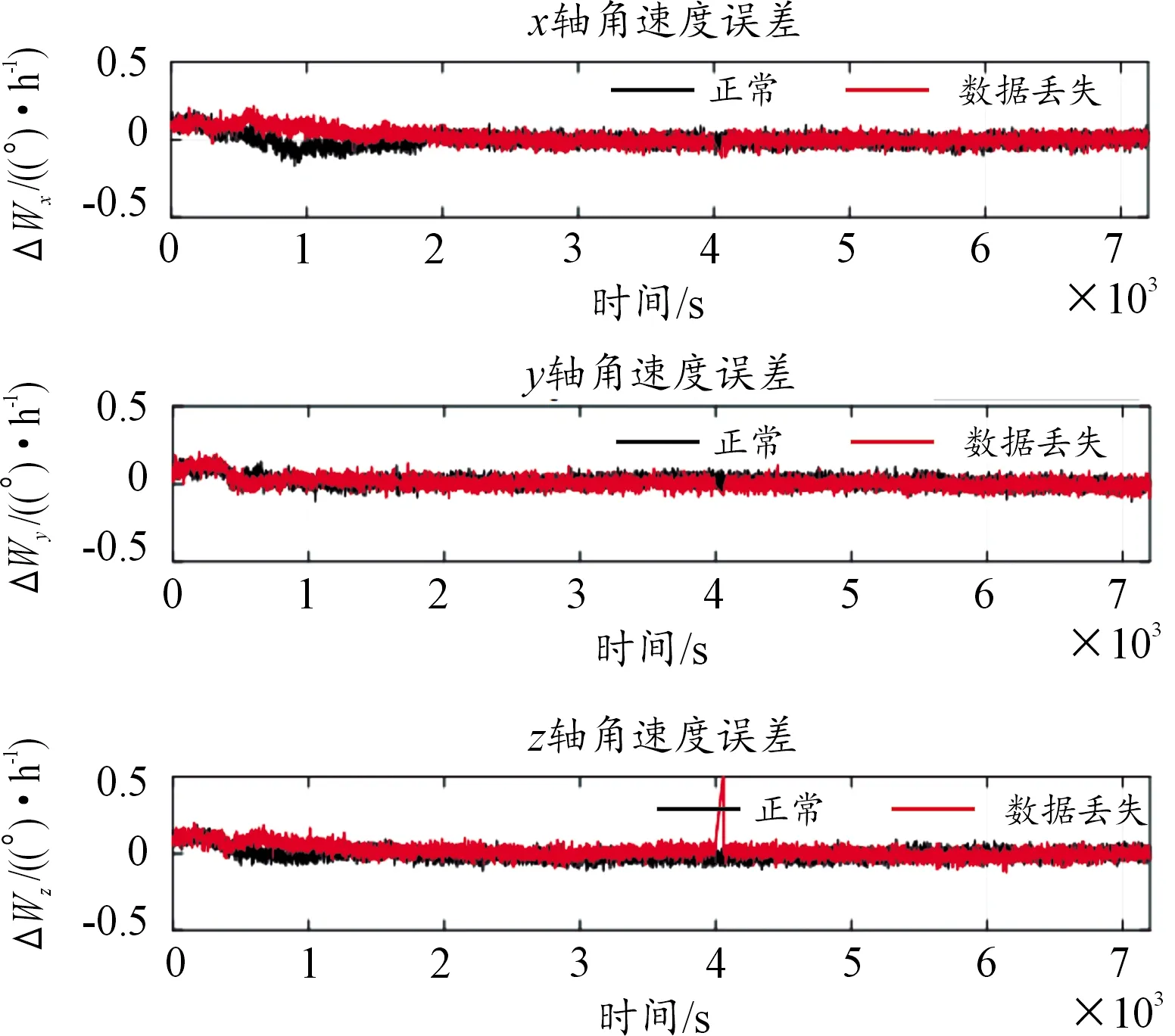
图6 基于星敏感器/陀螺的卫星角速度误差曲线

由图5、图6可以看出：无论是姿态角误差还是角速度误差，都能以较快的速度收敛至0，姿态角误差估计精度达到0.003°、角速度误差估计精度达到0.03°/h，并且短时间的陀螺仪数据丢失对卫星定姿的影响不大。

5 结论

本文针对遥感卫星对于高精度姿态信息的需求，提出了一种星敏感器/陀螺组合的卫星姿态确定算法。首先改进QUEST算法，准确判断四元数的正负，从而输出连续的四元数。将星敏感器所得的星光矢量经过改进QUEST算法处理后得到的姿态四元数作为EKF的量测数据，修正陀螺的漂移。通过数值仿真验证了此算法可以使系统获得较高的姿态估计精度。