水下滑翔机抗干扰非线性自适应控制方法

张文清，吕 勇，马士全

(1.海军潜艇学院，山东 青岛 266199；2.青岛海洋科学与技术国家试点实验室，山东 青岛 266237)

1 引言

水下滑翔机由于海上工作时间长、适用各种复杂海况，利用水下滑翔机、波浪滑翔器、水下无人潜航器等无人移动平台执行任务的活动日益增多，控制领域针对水下无人移动平台的非线性和欠驱动特性以及相关的控制方法的研究成为热点[1-4]。王丹[5]针对含有不确定性和环境扰动的自主海洋航行器的路径跟踪控制问题，结合动态面控制技术分别对全驱动自主海洋航行器和欠驱动自主海洋航行器进行路径跟踪控制器设计，提出了一种基于自适应动态面方法的路径跟踪控制策略，仿真结果表明了所给出控制算法的有效性。张庆闫[6]研究多约束条件下UUV的路径跟踪控制问题。通过对 Lyapunov系统理论及反步法设计了主从式多无人水下航行器的协同编队策略。实现了主从式编队约束下多无人水下航行器协同对给定期望路径的跟踪，并对设计的协同路径跟踪控制器进行了仿真验证。针对欠驱动无人水下航行器的三维空间路径跟踪控制问题，王宏健等[7]设计了跟踪误差反馈增益形式的线性控制项镇定位置跟踪系统，然后基于反步法设计动力学控制器，消除了部分非线性项，简化了虚拟控制量的形式，保证了闭环跟踪误差系统状态的一致最终有界。国内外文献针对AUV机动性强的无人平台相关研究较多，考虑水下滑翔机的欠驱动性与AUV有本质的区别。本文在考虑海流干扰条件下，建立了欠驱动水下滑翔机数学模型，并设计非线性控制器。采用视线导航算法，设计期望俯仰角和偏航角，得到轴向推力、俯仰力矩及偏航力矩，提出了一种欠驱动自主水下航行器的路径跟踪策略。

水下滑翔机工作原理见图1[8]。

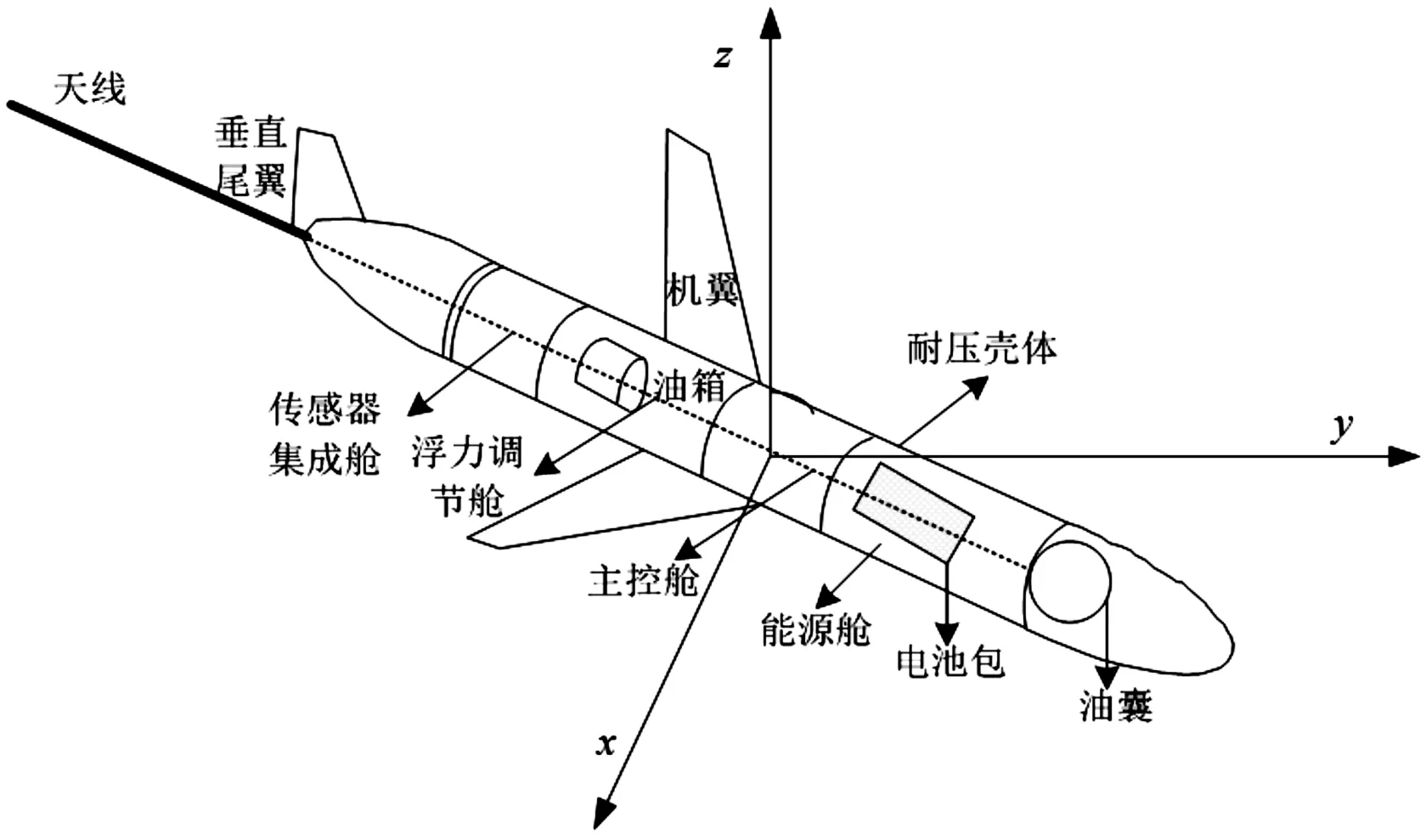
图1 水下滑翔机工作原理示意图

工作流程可以分为4个阶段：水面准备，滑翔下潜，滑翔上浮和水面等待。水下滑翔机在航行开始时，受到净浮力的作用漂浮在水面上。通过卫星通信或甲板无线通信收到控制指令后，水下滑翔机依靠浮力调节单元从外部油囊回油到内部油缸中，减少滑翔机自身的排水体积，使浮力小于重力，从而下沉；同时，姿态调节机构通过移动内部重物来改变重心位置，使水下滑翔机达到所需的姿态角；在下潜的过程中，它是借助水平翼和垂直尾翼受到的水动力，向前和向下滑翔，此时任务传感器进行数据测量工作。在到达预定的工作深度后，水下滑翔机通过浮力调节单元将油从内部油缸排到外部油囊中，增大滑翔机自身排水体积，使浮力大于重力，从而实现系统运动由下潜到上升过程的转变；同时姿态调节机构也进行工作，使其达到向上滑翔所需的姿态角。在滑翔过程中，水下滑翔机会通过姿态调节机构的实时调整自身姿态，使其按照设定的滑翔角和航向进行稳定滑翔运动，如果需要转弯姿态调节机构会通过转动内部重物来改变重心位置，借助横滚力矩和水动力矩的总和作用使水下滑翔机航行发生偏转。当完成工作任务返回水面以后，水下滑翔机会根据预设的程序，使通讯天线伸出水面，进行卫星定位，并通过卫星将测量的数据传输给控制中心，同时接受新的控制指令，进行下一次循环工作。

2 水下滑翔机数学模型建立

欠驱动水下滑翔机六自由度数学模型[3]为：

(1)

(2)

其中，

其中，X=(x,y,z,φ,θ,ψ)T，Ω=(φ,θ,ψ)T是惯性坐标系下位置和角度；υ=(u,v,w,p,q,r)T表示移动坐标系下的速度，满足以下条件：

(3)

本文控制系统设计目标是在存在未知的常值海流干扰和模型参数不确定[9]情况下，对油囊浮力、横滚力矩及俯仰力矩设计反馈控制律使AUG位置(x,y,z)精确跟踪期望轨迹(xd,yd,zd)，且所有闭环系统状态变量是有界的。

3 非线性跟踪控制器设计

水下滑翔机欠驱动非线性控制原理见图2。

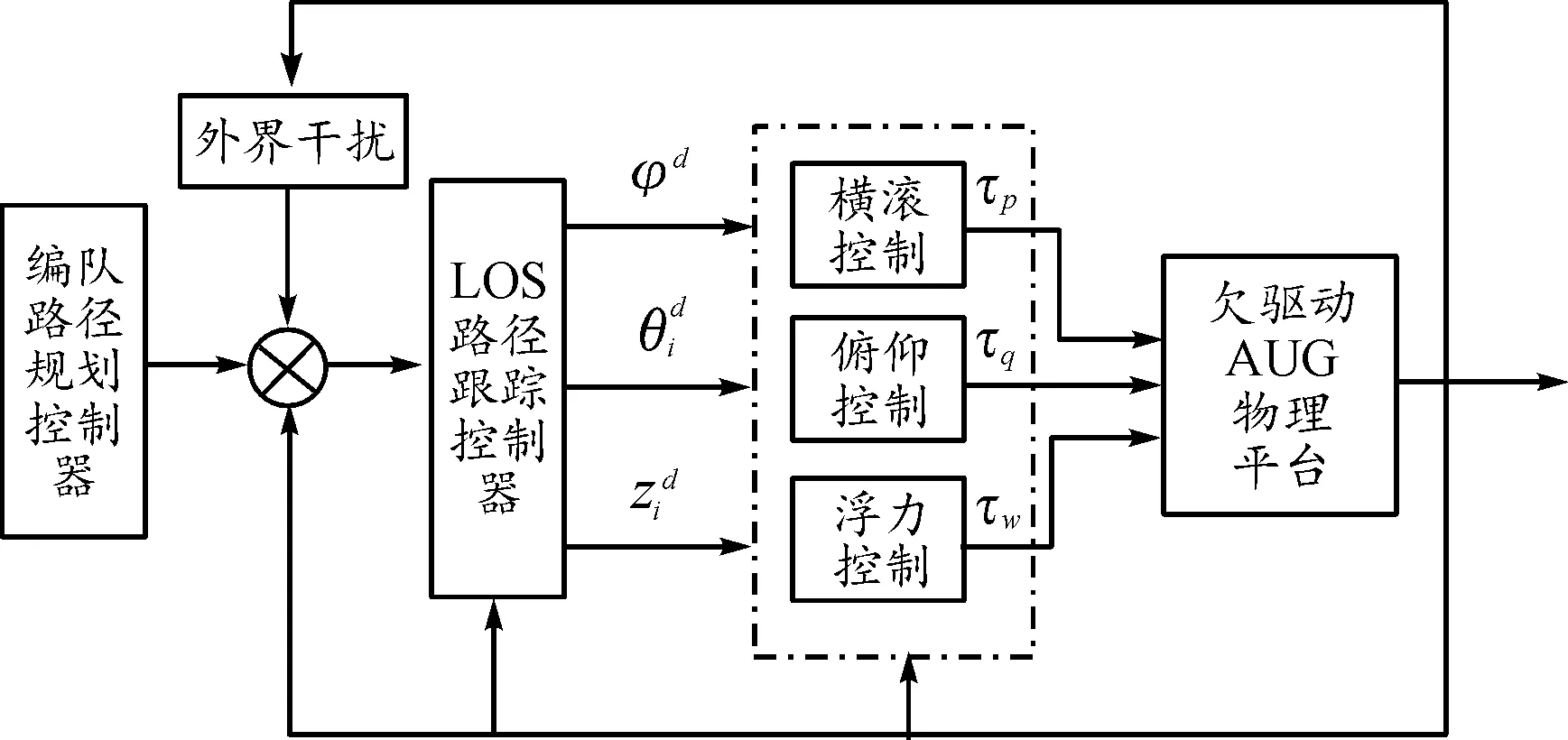
图2 欠驱动AUG非线性控制原理框图

定义跟踪误差：

e=(e1,e2,e3)T=QT(X-Xd)

(4)

s为期望路径算子[10]，以上符号对应关系如下：

则位置误差动态为

(5)

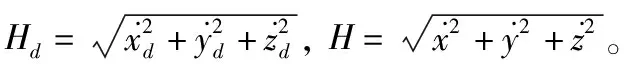
首先根据三维LOS视线导航算法[4]得到：

(6)

(7)

(8)

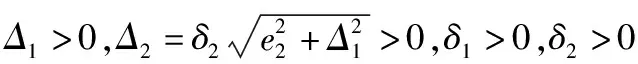
υδ=arcsin(sinρdcosρrcosγr+cosρdsinρr)

(9)

(10)

可知期望俯仰角和偏航角为：

(11)

(12)

设(ws,θs,ψs)为(wref,θref,ψref)滤波后的期望值，下面设计实际控制输入油囊浮力τw、横滚力矩τp和俯仰力矩τq。

定义

(13)

(14)

虚拟输入量设计为：

a3=ws

(15)

(16)

(17)

对式(13)和(14)两边求一阶导数，得

(18)

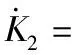
(19)

其中，

整理得到

(20)

对K2两边求一阶导数，结合AUG模型的动力学方程[11]，整理得到

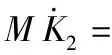
τ-(C(υ)+D(υ))K2-(C(υ)+

(21)

设计实际控制输入为

(22)

4 数值计算与仿真

数值仿真实验中水下滑翔机平台物理参数[12]如表1所示，对上述研究的路径跟踪控制方法的正确性和有效性进行验证。

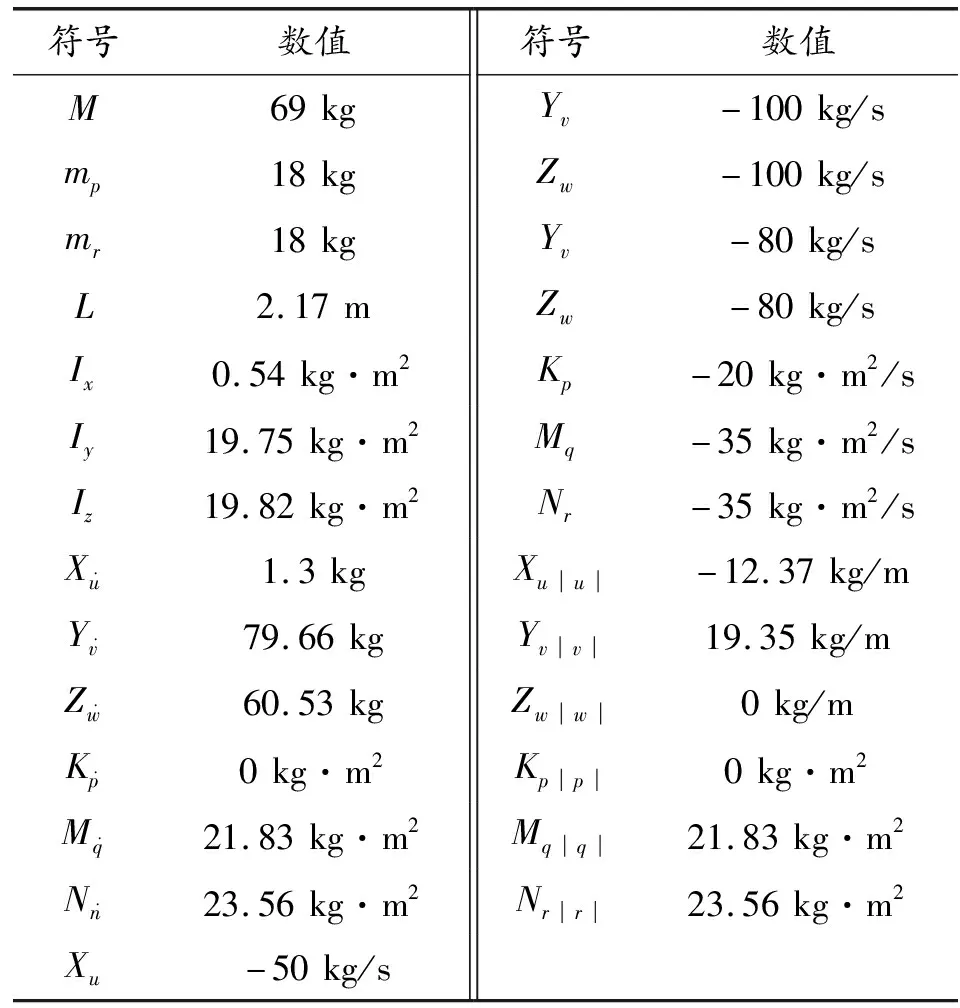
表1 水下滑翔机平台物理参数

仿真参数设置：坐标系采用东南地坐标系，仿真时间30 h，控制频率10 Hz，节点位置误差≤50 m；路径设计为不规则曲线，路径长度30 km左右，路径节点集合设定：xd=[0,5,10,15,20,25]，yd=[0,-3,-5,-5,-3,0]，单位km。单平台控制参数：横滚角控制kp=2 000，ki=0，kd=-1 000；纵倾角控制kp=2 000，ki=10，kd=-1 000；深度控制kp=2 000，ki=10，kd=-200。

1)海流大小1.0 kn，与纬度方向夹角8°条件下运行

设定水下滑翔机路径为不规则曲线，海流大小为1.0 kn，海流方向与纬度方向夹角8°条件下，水下滑翔机采用文中的抗干扰非线性自适应控制方法运行。

图3为水下滑翔机运行实际路径和期望路径的跟踪过程，由图可看出，在模型中存在未知海流干扰和模型参数未知的情况下，控制器可使水下滑翔机稳定跟踪期望轨迹，跟踪误差在10 m以内，达到了预期效果。

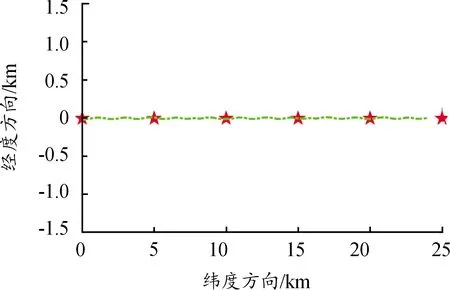
图3 水下滑翔机跟踪控制稳定运行曲线

如图4所示，可以看出水下滑翔机纵倾角度稳定跟踪设定值，下潜为-30°，上浮为+30°，达到了预期效果。

图4 水下滑翔机纵倾角度控制过程曲线

如图5所示，可以看出水下滑翔机横滚角度稳定跟踪设定值，实际横滚角度控制达到了预期效果。

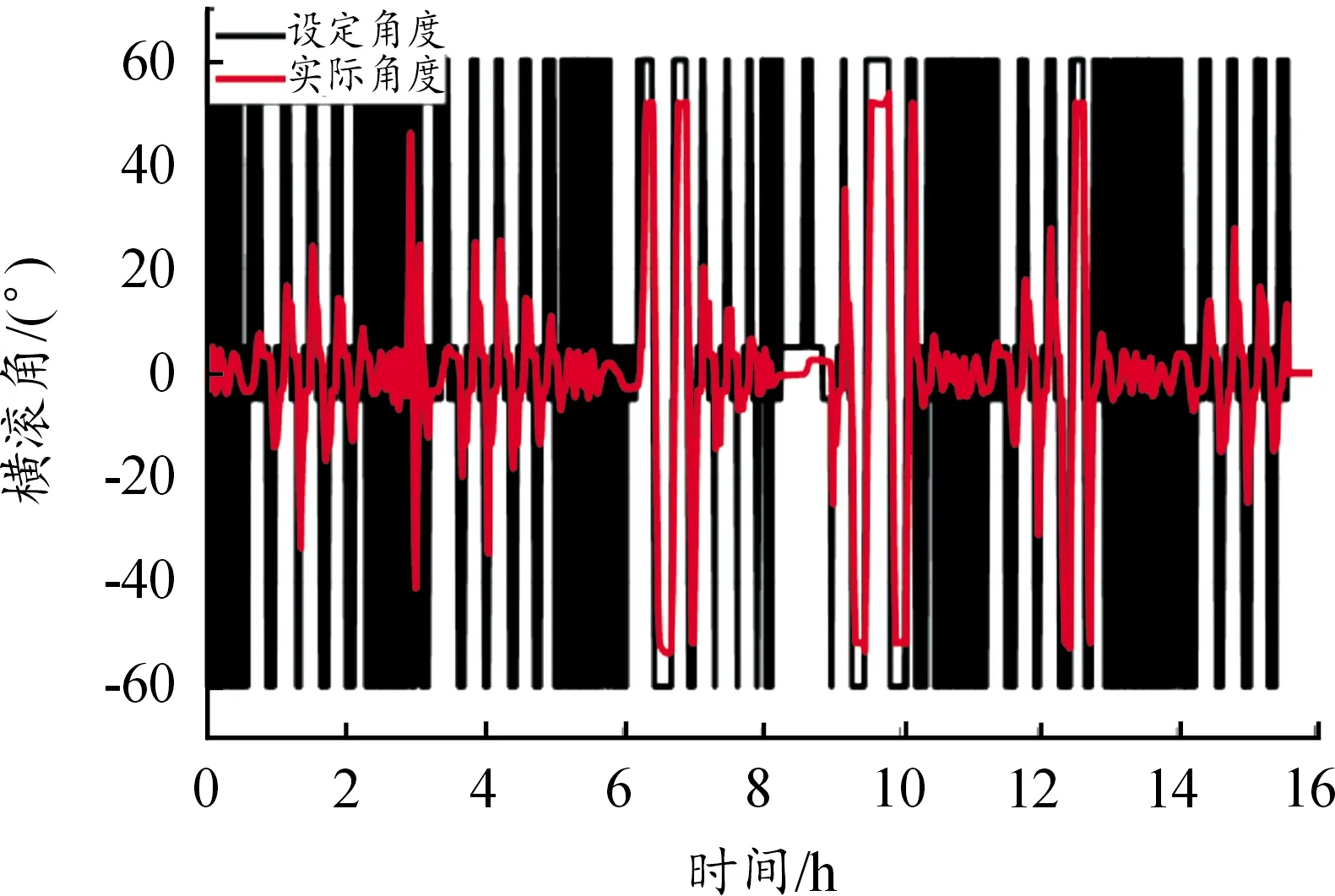
图5 水下滑翔机横滚角度控制过程图

2)海流大小1.0 kn，与纬度方向夹角10°条件下运行

在所有的仿真参数和水下滑翔机参数不变的情况下，设置海流大小1.0 kn，与纬度方向夹角10°，运行结果如图6所示，水下滑翔机个跟踪控制处于临界稳定状态，跟踪误差在50 m以内。

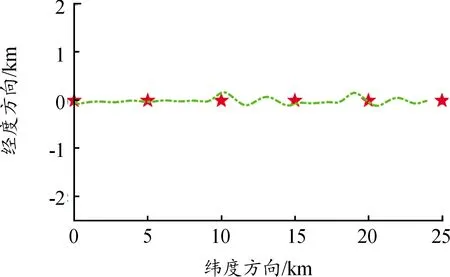
图6 水下滑翔机跟踪控制临界稳定曲线

3)海流大小1.0 kn，与纬度方向夹角12°条件下运行

在所有的仿真参数和水下滑翔机参数不变的情况下，设置海流大小1.0 kn，与纬度方向夹角12°，运行结果如图7所示，水下滑翔机跟踪控制逐渐发散。

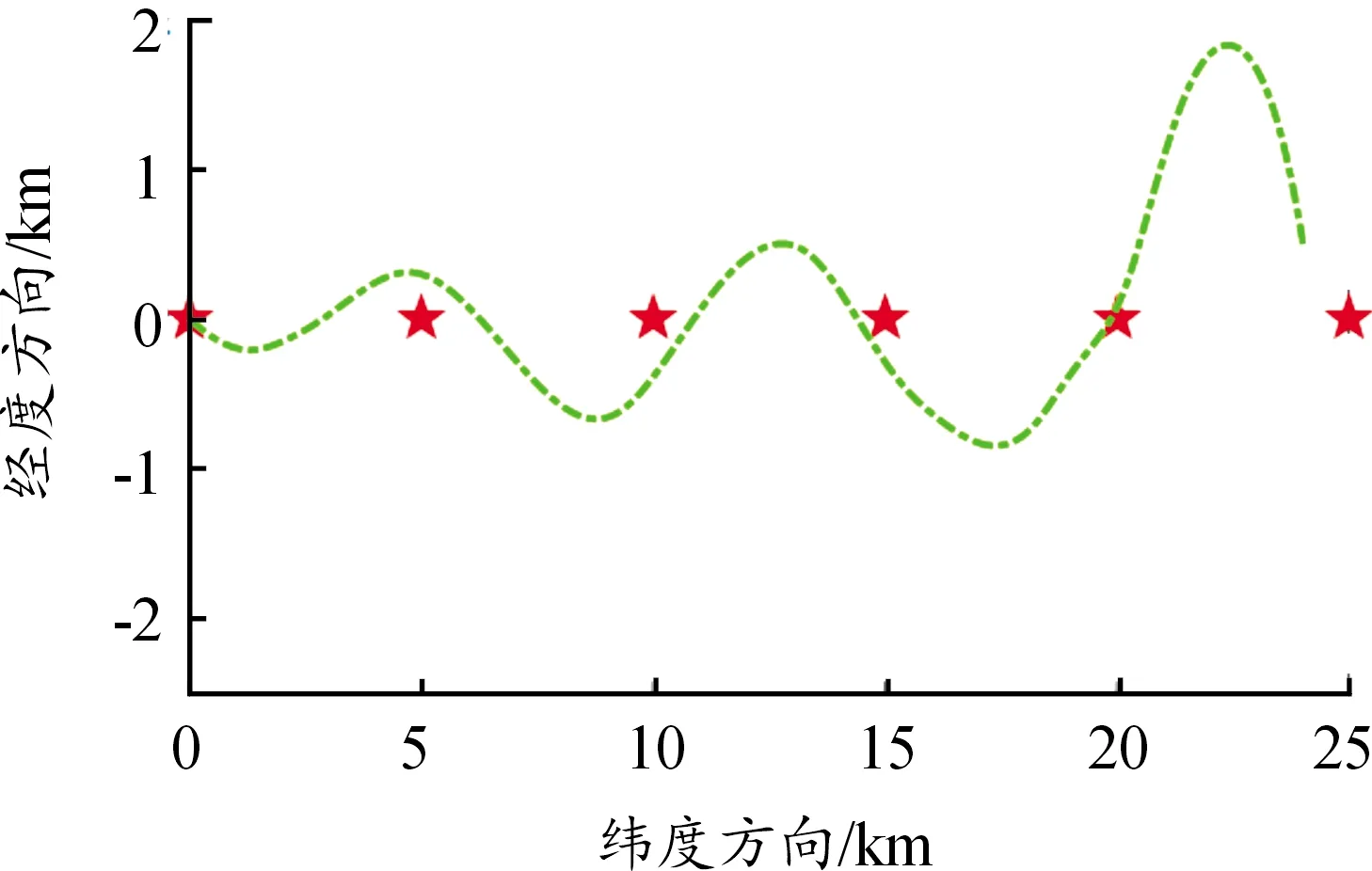
图7 水下滑翔机跟踪控制曲线

5 结论

本文研究了存在海流干扰条件下欠驱动水下滑翔机的路径跟踪问题，结合视线导航法建立了水下滑翔机的欠 驱动路径跟踪模型，并设计了非线性自适应控制策略。通过大量理数值仿真实验，分析了海流大小和方向不同情况下，水下滑翔机路径跟踪控制效果。① 海流大小1.0 kn，与纬度方向夹角8°条件下，水下滑翔机跟踪控制稳定运行；② 海流大小1.0 kn，与纬度方向夹角10°条件下，水下滑翔机跟踪控制临界稳定；③ 海流大小1.0 kn，与纬度方向夹角12°条件下，水下滑翔机跟踪控制逐渐发散。由此可以看出当海流大小和方向满足一定条件时，本文提出的控制器能够克服常值海流干扰及模型参数未知的影响，具有较好的鲁棒性和很好的跟踪效果。当然控制方法不可能适用所有海况条件，当海流大小和方向夹角超过一定值时，水下滑翔机跟踪控制会出现明显的发散。