电动负载模拟器的自适应模糊PI 控制策略

贾东旭，刘 梁，徐照平

（南京理工大学 机械工程学院，江苏 南京 210094）

0 引言

电动负载模拟器是一种在实验室条件下，能模拟舵机承受空气铰链力矩的半实物装置［1］。它的作用是在实验室条件下，实时给舵机施加载荷，模拟舵面受力情况，测试舵机系统的性能。电动负载模拟器的结构简单，维护方便，加载精度高，所以近年来得到了大量的研究。

目前，抑制多余力矩［2］与提高系统控制精度是电动负载模拟器研究的主要问题。虽然传统的控制策略对多余力矩有一定抑制能力，但由于电动负载模拟器系统中存在不确定因素，导致对多余力矩的抑制效果不理想，进而影响到系统的控制精度，而智能控制策略则可解决这个问题。

文献［3］在PID 反馈控制中引入迭代学习算法，以克制系统中非线性因素的影响，抑制多余力矩，提高系统精度。文献［4］设计了自适应滑膜控制，以消除系统中未知的不确定性对滑模变结构控制性能的影响，提高系统的动态特性。针对传统PID 控制器自适应性差的问题，文献［5-6］提出了模糊PID 控制。文献［7］提出了自适应模糊控制，以保证瞬态跟踪性能和最终跟踪精度。文献［8］提出了一种基于半模糊小脑神经网络（Cerebellar Model Articulation Controller，CMAC）的比例-微 分（Proportional-Derivative，PD）混合控制方法，解决不确定因素导致常规基于CMAC 的PD 混合控制方法的不稳定问题，抑制系统的多余力矩。

针对电动负载模拟器系统中的多余力矩抑制问题，文献［9］提出了径向基函数（Radial Basis Function，RBF）神经网络和重复控制PID 相结合的复合控制方法，以提高系统的抗干扰、自适应能力和跟踪性能。

本文在分析电动负载模拟器系统和建立其数学模型的基础上，设计了力矩微分负反馈校正环节和自适应模糊PI 控制器，以提高系统的动态加载性能，最后进行了实验验证。

1 电动负载模拟器系统与分析

1.1 电动负载模拟器的工作原理及其数学模型

电动负载模拟器主要由加载电机、传感器、驱动器和控制器组成，结构简图如图1 所示。系统工作时，控制计算机下达控制指令，力矩传感器和角度传感器分别将采集到的力矩信号、角度信号反馈到加载电机控制器，加载电机驱动器驱动加载电机工作输出力矩对舵机进行加载，弹簧杆连接于加载电机与舵机间，起到力矩缓冲的作用。

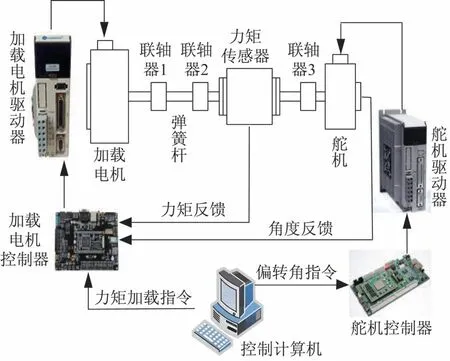
图1 电动负载模拟器结构简图Fig.1 Structure diagram of electric load simulator

由以上对电动负载模拟器的组成和工作原理的分析，得到其数学模型如图2 所示。

图2 电动负载模拟器数学模型Fig.2 Mathematical model of electric load simulator

图2 中：um为加载电机驱动器的输入电压；Tl为系统输出力矩；θr为舵机端输出转角；La、Ra、Ja和Ba分别为加载电机绕组电感、绕组电阻、转动惯量和阻尼系数；KPWM、Kea和Kta分别为加载电机驱动器功率放大系数、加载电机反电动势系数和加载电机转矩系数；TA为弹簧杆连接刚度系数；s为拉普拉斯变换的复变量。

由图2 可得出系统的传递函数为

式中：Um（s）、θr（s）和Tl（s）分别由um、θr和Tl经拉普拉斯变换所得。

数学模型建立之后，在此给出舵机和加载电机的主要性能参数如下：舵机的额定转矩0.32 N·m，额定转速3 000 r/min；加载电机额定转矩0.44 N·m，额定转速3 000 r/min。

1.2 系统多余力矩与不确定因素分析

多余力矩是当加载系统的力矩输入指令为零时，加载系统跟随舵机系统运动输出的力矩。由式（1）可知，系统的输出力矩由两部分组成，其中，第2部分“-θr（s）G（2s）”是由舵机的运动产生的力矩，该部分即为多余力矩。

电动负载模拟器系统中的多余力矩主要由两部分组成［10-12］：一部分是加载电机随动产生的电磁转矩；另一部分是加载电机的多余惯量引起的惯量多余力矩。电动负载模拟器系统工作时，舵机在偏转角指令下做主动转动，加载电机在力矩加载指令下与舵机同轴，被动跟随舵机运动，这种被迫运动会引起加载指令力矩之外的电磁转矩；加载电机在转动过程中，电机转子和连接轴的转动会产生惯量，这个惯量就是多余惯量，由于多余惯量的存在，即使很小的角速度也会产生多余力矩。系统中由于多余力矩的存在，加载电机加载到舵机的力矩势必会受到影响，不会完全按照力矩加载指令进行加载，从而影响到系统的动态特性和加载精度。

电动负载模拟器系统中存在一些不确定非线性因素［13-14］，包括驱动器的影响、电机参数的摄动、摩擦非线性和间隙非线性，都会影响多余力矩的抑制，增大抑制多余力矩的困难性，影响系统性能。

1.3 系统特性分析

由1.1 节建立的数学模型可知，影响系统性能的主要是系统连接刚度和转动惯量2 个参数。系统连接刚度对系统谐振频率和多余力矩的影响的频率特性Bode 图分别如图3 和图4 所示。由图3 和图4 可知，当其他条件不变，连接刚度TA分别为10、50、100 N·m·rad-1时，对应的谐振频率分别为135、242、343 Hz，对应的扰动通道多余力矩谐振峰值分别为24.8、45.5、54.8 dB，即随着连接刚度增大，系统的谐振频率随之增加，系统在无扰情况下的加载带宽也增大；多余力矩的谐振峰值随之增大，系统的多余力矩增大。

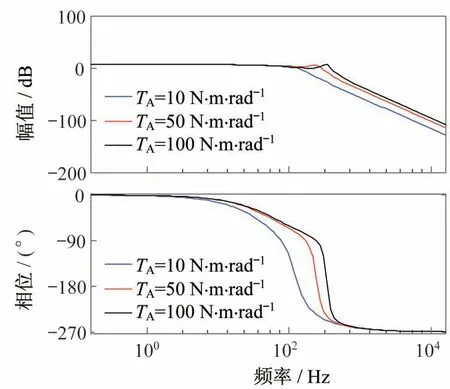
图3 不同连接刚度的系统无扰开环频率特性Bode 图Fig.3 Bode diagram of system undisturbed open-loop frequency characteristics at different connection stiffness

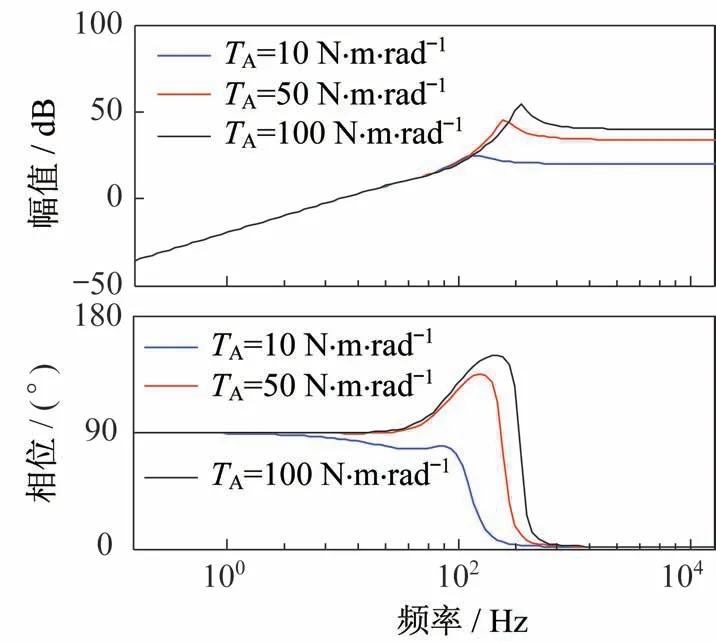
图4 不同连接刚度时系统扰动通道频率特性Bode 图Fig.4 Bode diagram of system disturbance channel frequency characteristics at different connection stiffness

系统转动惯量对系统谐振频率和多余力矩的影响的频率特性Bode 图分别如图5 和图6 所示。由图5 可知，当其他条件不变，转动惯量Ja分别为0.01、0.10、1.00 kg·m2时，对应的谐振频率分别是6.300、2.360、0.739 Hz，即转动惯量越大，谐振频率越小，系统无扰情况下的加载带宽也就越小；由图6可知，在低中频段，系统的多余力矩的幅值随着转动惯量的增大而增大，相位也更加超前，影响系统的加载性能。

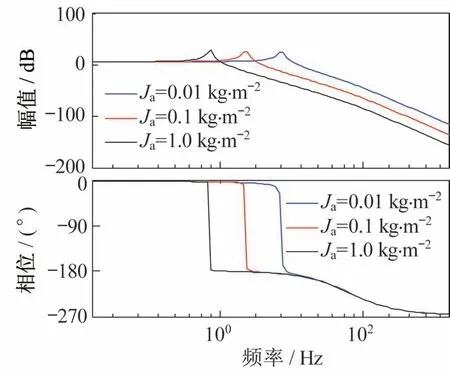
图5 不同转动惯量的系统无扰开环频率特性Bode 图Fig.5 Bode diagram of system undisturbed open-loop frequency characteristics at different moments of inertia

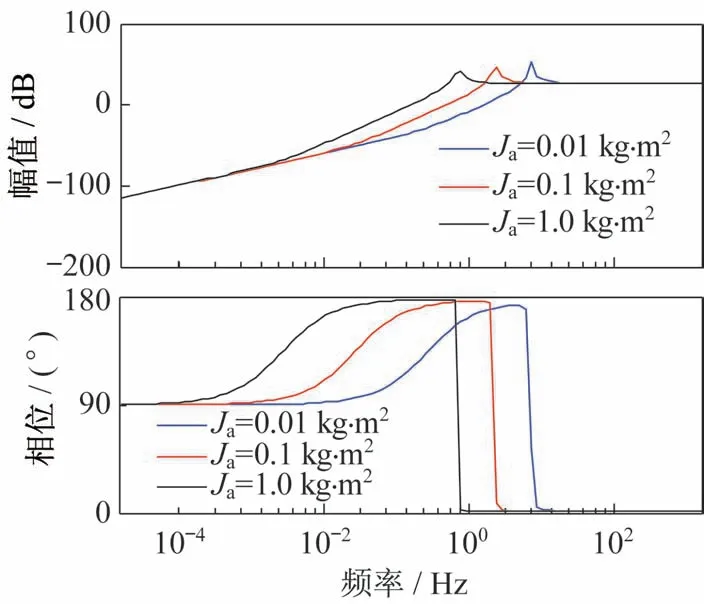
图6 不同转动惯量时系统扰动通道频率特性Bode 图Fig.6 Bode diagram of system disturbance channel frequency characteristics at different moments of inertia

2 控制器的设计

2.1 力矩微分负反馈环节设计

反馈校正能减小被包围环节时间常数、非线性特性的影响和对参数变化的敏感性，尤其是微分负反馈校正［15］。本文将微分负反馈校正引入系统中，对电动负载模拟器的输出力矩进行微分形成力矩变化速度，将此变化速度作为反馈信号，最终形成反馈环节。考虑到纯微分环节较难实现，加入1 个惯性环节1/（1+τs）作为低通滤波器，形成最终的力矩微分负反馈校正环节Kfds/（1+τs），其中，Kfd为微分反馈环节的时间常数，τ为低通滤波器的时间常数。

该微分环节与常规PID 控制器微分环节相比，噪声干扰作用更低，使系统的抗干扰能力更强，稳定性更好。加入力矩微分负反馈环节的电动负载模拟器系统的结构框图如图7 所示。图中，Tin为输入指令力矩。

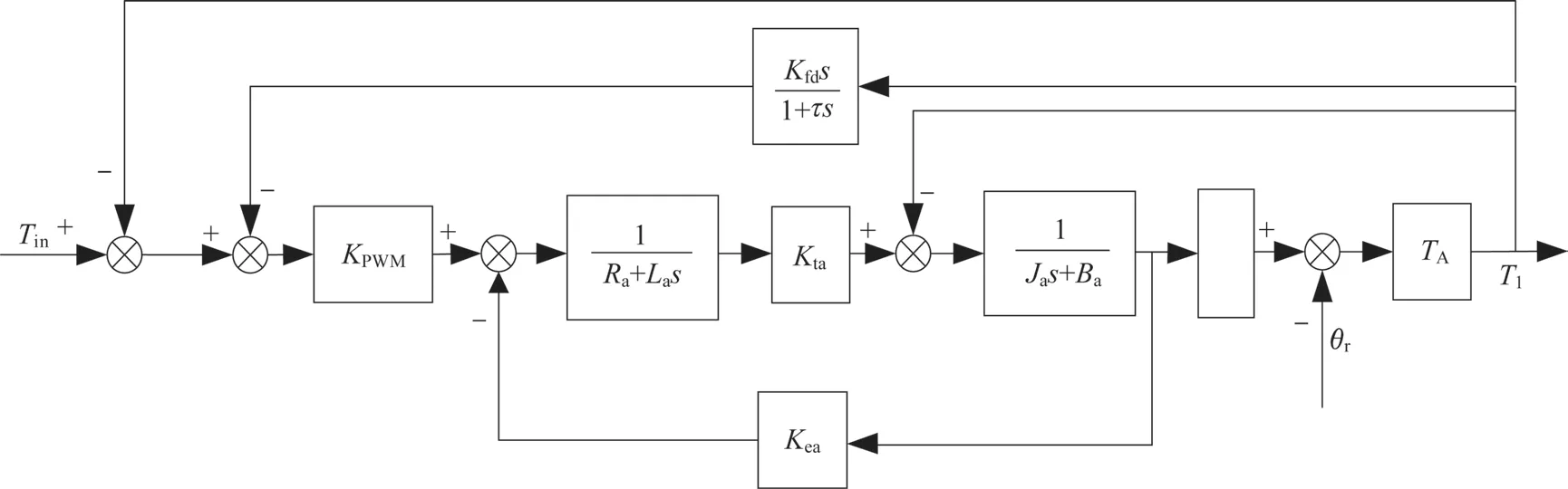
图7 引入力矩微分负反馈的电动负载模拟器系统结构框图Fig.7 Block diagram of electric load simulator system with torque differential negative feedback

2.2 自适应模糊PI 控制器设计

自适应模糊PI 控制器作为PI 控制器与模糊控制器的复合形式，既具有PI 控制器结构简单的优点，又具有模糊控制器自适应性高的特点，可在线自整定PI 控制器的参数，弱化系统非线性因素的干扰，使整个控制系统具有良好的动静态加载特性。

自适应模糊PI 控制器将系统的误差e和误差变化率ec作为输入，在控制器内部，根据制定的模糊规则对PI 控制器的KP（比例系数）、KI（积分系数）2个参数进行自整定，基本控制算法为

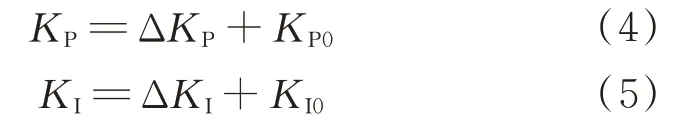
式中：ΔKP、ΔKI是PI 控制器的修正参数，是模糊控制器的输出；KP0、KI0是PI 控制器的初始值。

自适应模糊PI 控制器的控制结构框如图8 所示。图中，r和y是电动负载模拟器系统的输入和输出，u为自适应模糊PI 控制器的输出。

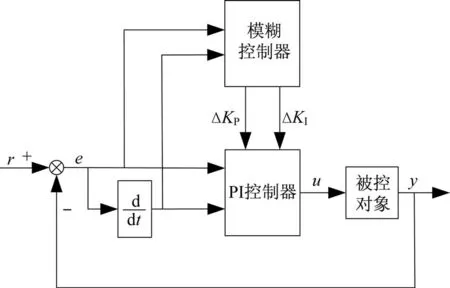
图8 自适应模糊PI 控制器结构框图Fig.8 Block diagram of the adaptive fuzzy PI controller

根据以上分析可知，所设计模糊控制器为双输入双输出结构。取输入e、ec和输出ΔKP的模糊集为｛NB，NM，NS，ZO，PS，PM，PB｝，输出ΔKI的模糊集为｛ZO，PS，PM，PB｝，隶属度函数均取为易实现的均匀三角形函数。根据PI 控制器的参数整定原则和实际操作经验，可列出ΔKP、ΔKI的模糊规则表，见表1 和表2。

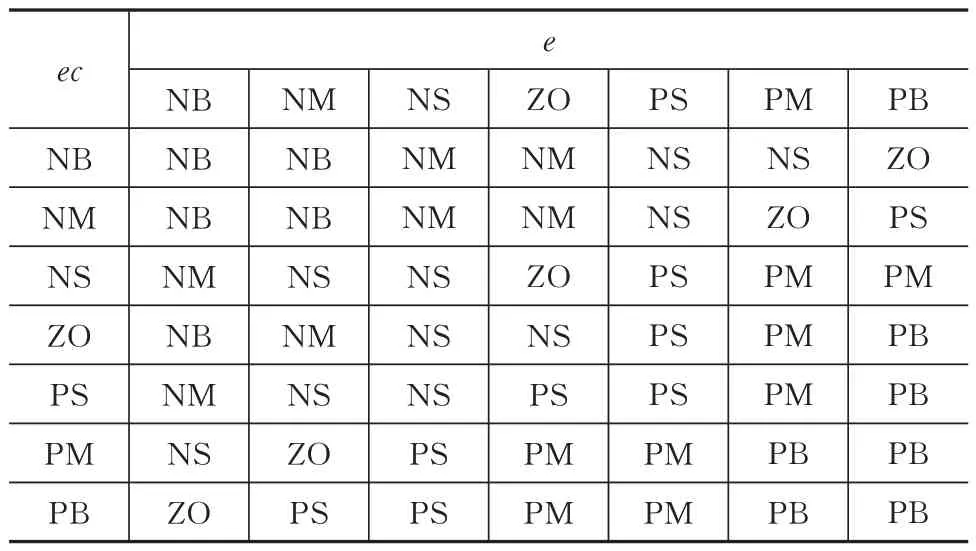
表1 ΔKP的模糊规则表Tab.1 Fuzzy rule table of ΔKP

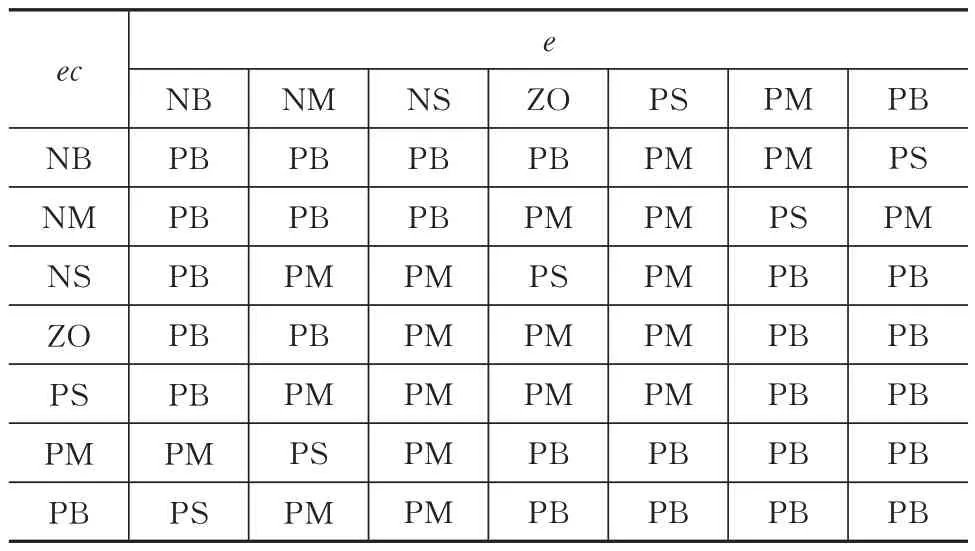
表2 ΔKI的模糊规则表Tab.2 Fuzzy rule table of ΔKI

最后采用Mamdani 推理算法模糊推理，得出1个模糊输出量，再经重心法对模糊输出量反模糊化，完成自适应模糊PI 控制器的设计。

考虑到系统中产生的多余力矩是无延迟地对系统产生干扰，需对多余力矩进行无延迟抑制。凡经控制器控制的方法都有延迟，不能对多余力矩进行及时抑制，因此，引入前馈补偿法进一步对多余力矩进行抑制。

3 仿真验证与分析

为验证所设计自适应模糊PI 控制器的有效性，在Matlab 中进行了仿真验证。

仿真给定系统的力矩输入指令为0 N·m，舵机的位置干扰信号为幅值10°，频率分别是6、10 Hz 的正弦曲线。仿真时，分别对比了系统不加任何控制和补偿时，开环控制的多余力矩与自适应模糊PI 控制时的多余力矩，舵机位置信号频率为6、10 Hz 时的多余力矩曲线如图9 和图10 所示。

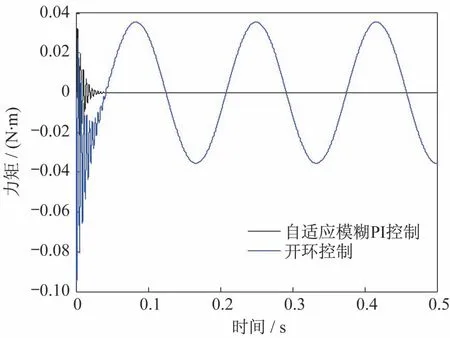
图9 舵机位置信号频率为6 Hz 时系统多余力矩Fig.9 System surplus torque when the servo position signal frequency is 6 Hz

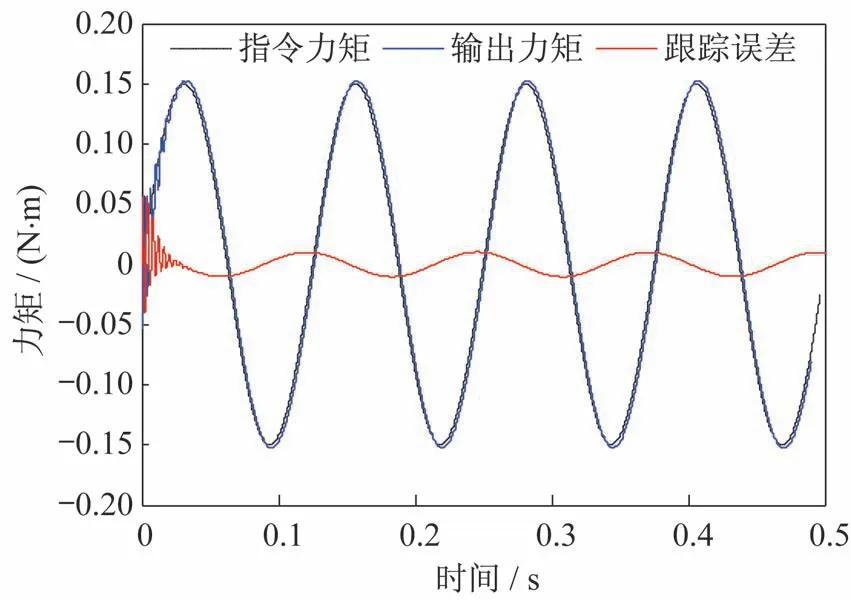
图10 舵机位置信号频率为10 Hz 时系统多余力矩Fig.10 System surplus torque when the servo position signal frequency is 10 Hz

由图9可知，舵机位置信号频率为6 Hz时，系统多余力矩由自适应模糊PI控制前的3.553×10-2N·m降为了控制后的1.894×10-5N·m；由图10 可知，舵机位置信号频率为10 Hz 时，系统多余力矩由自适应模糊PI 控制前的5.888×10-2N·m 降为了控制后的8.932×10-5N·m。控制后的多余力矩被抑制了99%以上，满足了系统的性能要求，从而证明了所设计的控制方法对多余力矩的抑制效果是良好的。

给定系统的力矩输入指令为幅值0.15 N·m，频率8 Hz 的正弦信号，舵机的位置干扰信号为幅值10°，频率10 Hz 的正弦曲线，得到了自适应模糊PI控制时的力矩跟踪曲线如图11 所示。

图11 自适应模糊PI 控制力矩跟踪曲线Fig.11 Torque tracking curve obtained by the adaptive fuzzy PI controller

由图11 可知，输出力矩曲线几乎与指令力矩曲线重合，相位滞后4.03°，跟踪误差峰值为1.023×10-2N·m，跟踪误差控制在了10%内。说明设计的自适应模糊PI 控制器满足“双十”指标要求（“双十”指标，是指在系统的最高工作频率下输出力矩相比于力矩加载指令幅值变化不大于10%和相角变化不大于10°），具有良好的控制性能。

4 实验验证

4.1 实验结果

为验证所设计控制器有效性，进行了实验验证，实验平台如图12 所示。

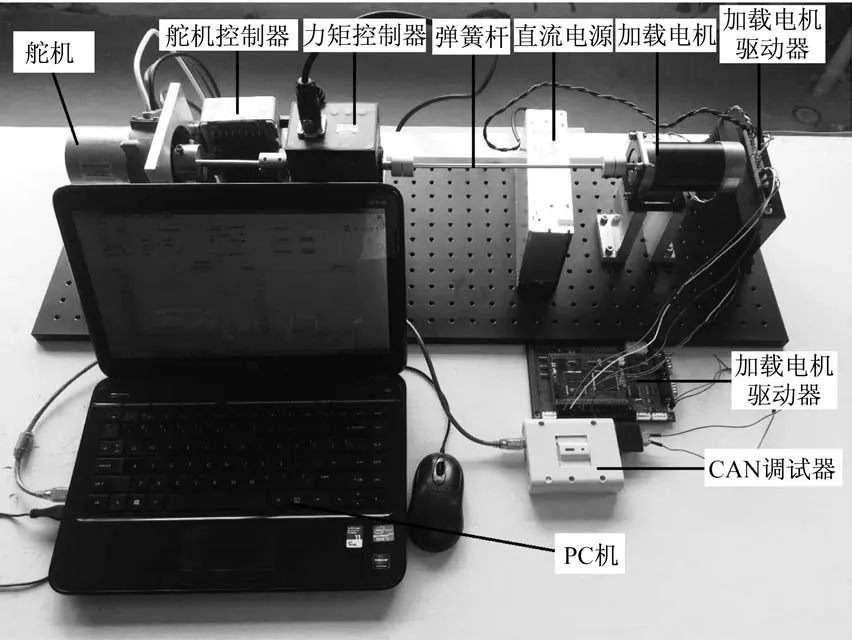
图12 加载系统实验平台Fig.12 Loading system test platform

首先对多余力矩的抑制效果进行实验，此时令指令力矩为0 N·m，舵机运动指令为幅值10°，频率10 Hz 的正弦曲线，所得多余力矩的抑制实验结果如图13 所示。

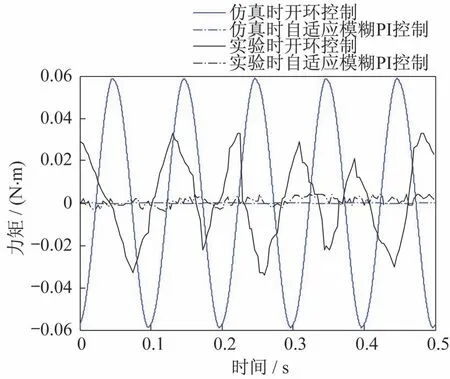
图13 多余力矩曲线Fig.13 Surplus torque curve

动态加载实验结果如图14 所示。此时给定指令力矩为幅值0.15 N·m，频率8 Hz 的正弦信号，舵机运动指令为幅值10°，频率10 Hz 的正弦曲线。

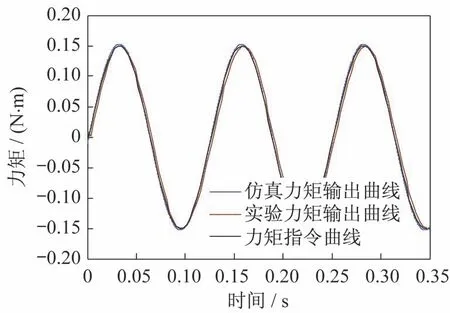
图14 动态加载曲线Fig.14 Dynamic loading curve

4.2 实验结果分析

由图13 可得：实验时开环控制多余力矩的幅值为0.033 N·m，自适应模糊PI 控制时的多余力矩幅值为0.004 N·m，多余力矩抑制率为87.9%；与仿真结果相比，实验所得多余力矩抑制效果虽然没有那么理想，但同样达到了一般工程上要求的85%以上，从而证明多余力矩的抑制效果是良好的。

由图14 可得：实验时系统达到稳态时的最大误差为0.012 7 N·m，占加载指令幅值的8.47%，相位滞后8.64°，满足了“双十”指标要求；仿真时系统达到稳态时的最大误差为0.011 35 N·m，占加载指令幅值的7.57%，相位滞后5.4°；实验结果与仿真结果相比，最大误差较大且相位较滞后。

由以上结果分析可知，实验时的结果可满足系统性能指标要求，但与仿真结果相比，结果并不理想，原因是实验台架中存在的未被消除掉的不确定因素及非线性因素的干扰，且仿真时建立的数学模型不准确，需进一步改进和完善。

5 结束语

本文设计了电动负载模拟器的系统方案，介绍了系统的工作原理，并分析了系统多余力矩的产生原理及系统中存在的不确定因素。针对系统存在的多余力矩及不确定因素，设计了力矩微分负反馈校正环节，在此基础上设计了自适应模糊PI 控制器，并结合前馈补偿对多余力矩进行抑制，以提高系统动态加载性能。仿真结果表明，所设计方法可将多余力矩抑制99%以上，抑制效果明显，且力矩动态跟踪满足“双十”指标，使电动负载模拟器系统具有较好的动态加载精度。最后进行了实验验证，结果表明，多余力矩抑制效果虽不如仿真所得结果理想，但可达到一般工程要求的85%以上，抑制效果良好，动态加载实验也能够满足“双十”指标，验证了所设计控制器的有效性。