防空武器系统能力需求分析的简化方法

陈 杰，谭天乐，史树峰

（1.上海航天技术研究院，上海 201109；2.上海航天控制技术研究所，上海 201109）

0 引言

近程末端防空武器在承担要地防空和机动伴随防空作战时，主要打击武装直升机、无人机，以及低空、超低空突防的精确制导武器。防空反导的作战方法一直在不断变化，攻击方式从原有的超低空突防、隐身突防、电子对抗、诱饵欺骗、精确饱和打击等，逐渐发展出一些新的作战武器和手段，例如，防区外发射精确制导弹药、中近程弹道导弹、高超音速巡航弹和无人机群等［1］。为此，需要重新梳理防空武器系统的能力建设需求，提出面对新威胁的发展思路。针对防空作战任务，寻找从“任务”到“能力”的定量映射关系，分析构建适应防空作战任务的能力需求及能力体系［2］。

防空作战本质上是“攻与防”的博弈对抗［3］。从防御者的角度来看，防空反导在物理数学上可抽象为在作战全阶段（初段、中段、末段），实现“防御导弹”与“攻击目标”的“空间域、时间域、速度域、精度域”之间的多域匹配问题［4］，如图1 和表1所示。

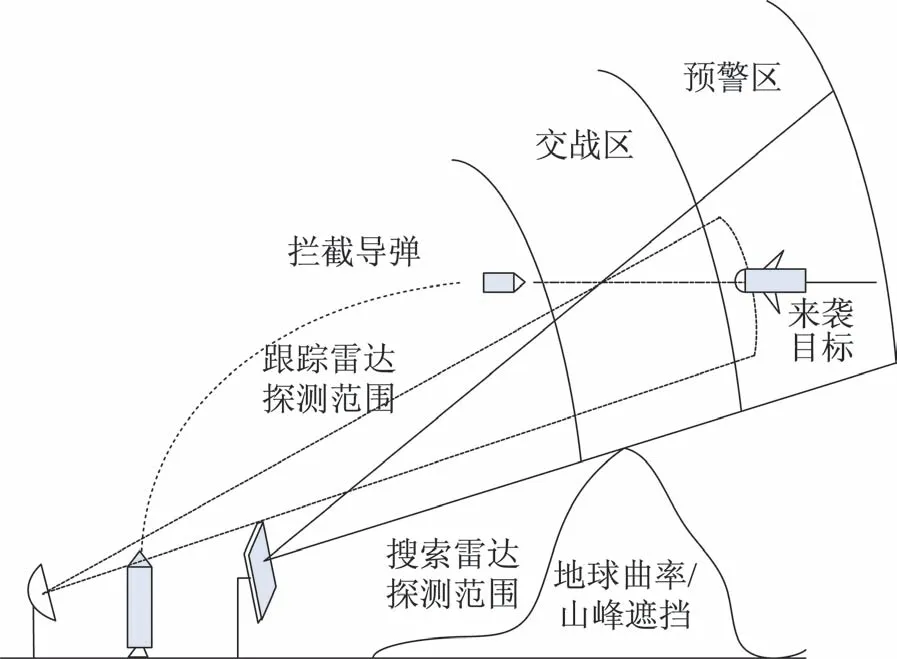
图1 防御对抗示意图Fig.1 Schematic diagram of defensive confrontation

表1 传感器、拦截弹、指挥控制、通信链路的域属性Tab.1 Domain properties of sensors，interceptors，command &control systems，and communication links

防御系统首先需要探测到目标。“武器系统火力发射距离，仅限其传感器探测距离”，即传感器作用空域需考虑视线遮挡“可观性”问题以及基于信噪比/信杂比的“可探性”问题。目前常见的各类传感器包括采用雷达、可见光、红外、激光等，用于探测发现、跟踪定位、目标识别、火控制导、末端制导、引信引爆和效果评估中，其中监视与跟踪是最为关键的问题［5］。其次，武器系统对威胁目标的防御可归结为传感器作用空域、威胁目标、防御武器三者之间的时空关系，确保特定威胁目标不能穿透防御交战区，这里称为防御武器对威胁目标的“可防性”问题。下面分别对可观性、可探性及可防性问题进行分析。

1 传感器的可观性分析

目前的高超声速巡航导弹、战术导弹、无人机等目标存在发现难、探测难以及跟踪难的问题。受地球曲率影响，单个地基雷达难以远距离发现目标。而空基平台则受到国界、地域的限制，不具备全天候工作能力。

分析地基探测系统中地球曲率对目标探测的视线影响（暂不考虑山峰遮挡影响）。对于小范围区域作战，将地球近似为平均半径Re为6 371 km 的球体。如图2 所示，若传感器A距离海平面高度为H0，其最低可视擦地角为γ（负向，顺时钟）可通过Re、H0计算获得，从而得到OB之间弧长L1和AB直线距离x如下：

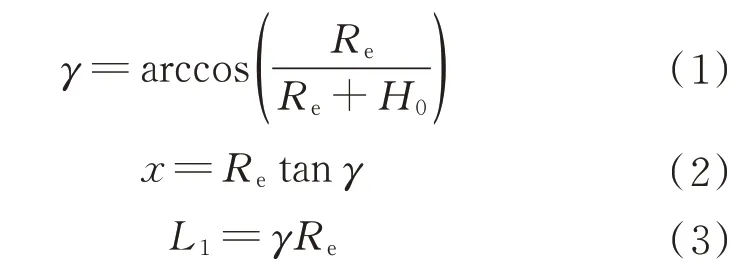
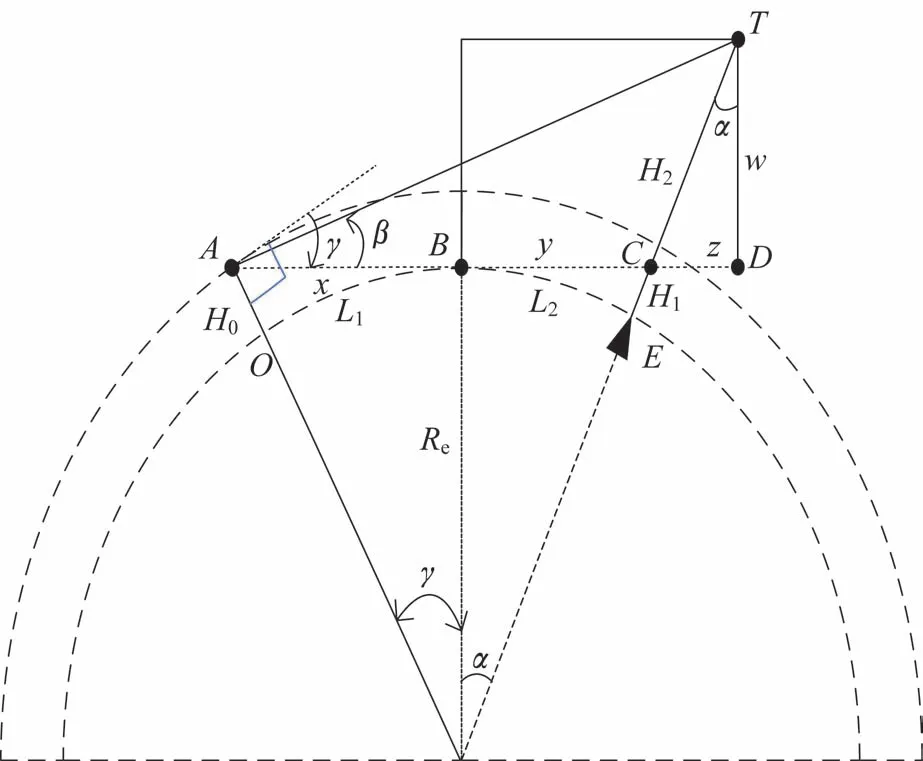
图2 传感器视线可观距离与高度关系Fig.2 Relationship between observable distance of a sensor and height of a threat target

以AB为0°基准，逆时针方向计算擦地角β，威胁目标位于T处。由BE弧长L2，其对地心张角α，BC长度y，CD长度z，DT长度w，EC高度H1，ET总高度H2，则威胁目标可观距离L=L1+L2与H2关系为

式中：

若H0已知，则

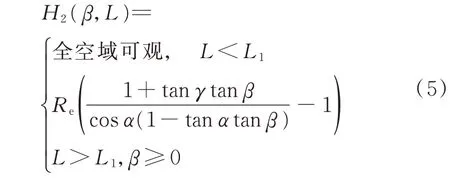
下面举例说明。

1）雷达部署于预警机典型工作高度（H0=0.9 km）。弧长L1=107.08 km，弧L1上空的任何目标均可观。对于弧长大于L1的空域，可求出擦地角β分别为0°、1°、2°时，H2随L的变化关系如图3（a）所示。

2）雷达部署于地面（H0=0 km）。此时γ、L1均为0，不同擦地角情况下L与H2之间的关系如图3（b）所示。以β=1°情况为例，不同飞行高度目标的可视距离见表2。

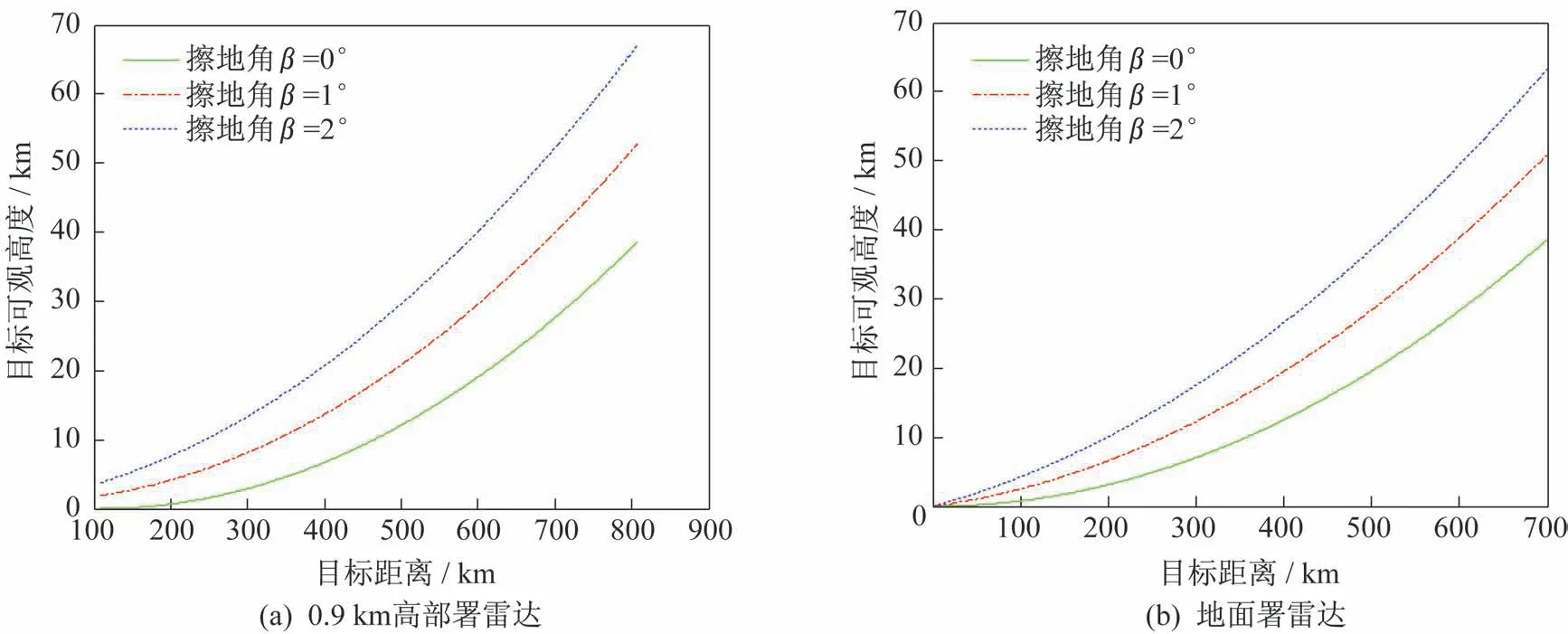
图3 不同传感器部署高度与擦地角情况下，目标距离与最低可观高度之间关系Fig.3 Relationship between target distance and minimum observable height for different radar deployment altitudes and grazing angles

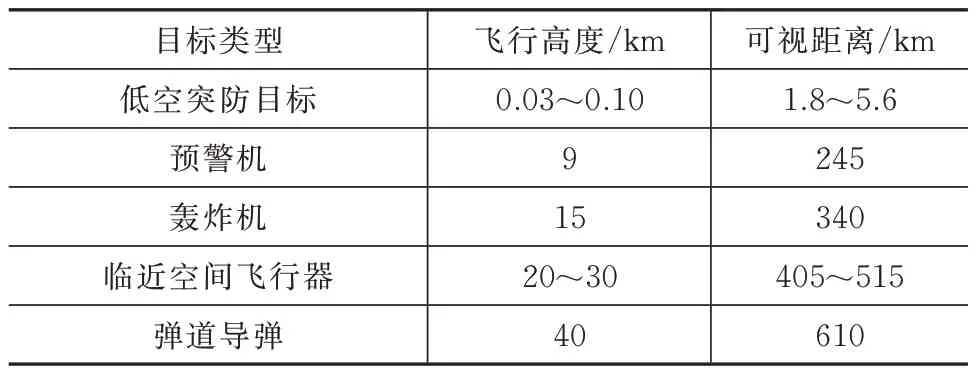
表2 不同飞行高度目标的可视距离Tab.2 Visual distance of targets at different altitudes

可观性分析表明，应重点考虑地球曲率对雷达可观探测距离的遮挡影响，可采用架高雷达，或降低雷达观测擦地角来解决可观性问题。

2 传感器的可探性分析

高超音速巡航导弹、战术导弹等目标移动速度快，会引起雷达信号频谱变化，导致雷达信息与滤波速度不匹配，目标探测过程出现阻碍，进而影响雷达对高速目标的探测，这些可通过雷达技术改进解决。本章仅从信噪比角度对探测制导雷达的可探性进行分析，其他类型传感器的可探性分析也可参考［6］。

探测与制导雷达可实现俯仰、方位角以及距离的三维空间定位，并通过多普勒效应和角度变化率测量目标的相对运动速度。依据雷达方程［7-8］，有

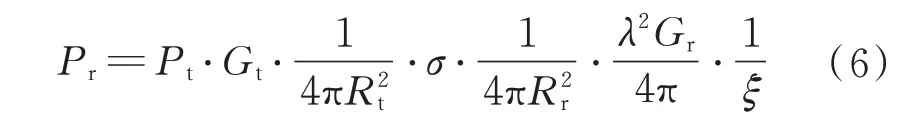
式中：Pr为接收到的回波功率；Pt为发射机峰值功率；Gt为定向天线增益为照射功率密度减少因子；σ为目标反射截面积或目标雷达散射截面积（Radar Cross Section，RCS）为功率密度减少因子；λ2Gr/(4π)为回波接收功率，其中，λ为雷达中心波波长，Gr为接收天线增益；1/ξ为系统损耗与传输损耗。

若Gt=Gr=G，Rt=Rr=R，则天线增益G表示为

即G与天线有效面积A成正比，与λ2成反比。式（6）可简化为

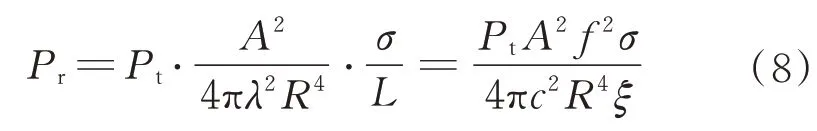
式中：f为雷达波中心频率为光速。

由于雷达在接收信号回波时会引入电噪声，其功率定义依据奈奎斯特定律有

式中：k为波尔兹曼常数；Te为以绝对温度表示的有效噪声温度；Bn为雷达噪声带宽（近似等于雷达单脉冲带宽）；Fn为噪声系数。

进而可以定义雷达接收机的信噪比（Signal to Noise Ratio，SNR）和可检测出的最小信噪比：

式中：rSN为信噪比；rSN0为最小信噪比。定义雷达最小可检测信号Smin为

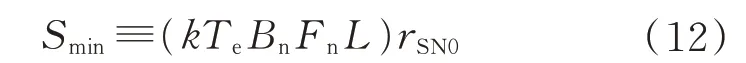
雷达最远探测距离Rmax表示为

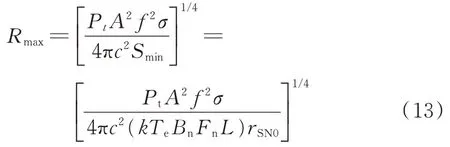
式（13）表明：Pt、A、f和σ越大，雷达可探测距离就越远；Te、Bn、Fn、L、rSN0越大，雷达可探测距离就越近。

若已知某目标截面积σ1的探测距离Rmax(σ1)，其他目标截面积σ2的探测距离Rmax(σ2)可通过下式近似地获得：

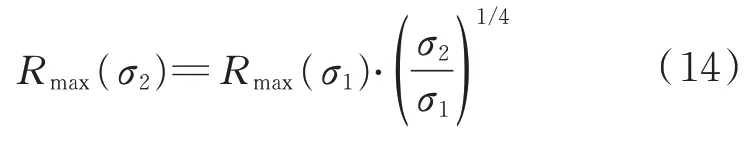
当L=1，可得

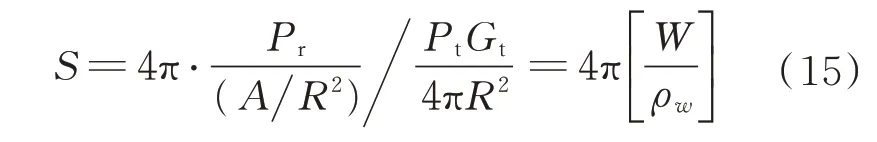
式中：S为RCS；W为接受天线单位立体角接受的目标回波功率；ρw为目标处的照射功率密度。

下面举例说明，选择某型雷达［8］，其参数见表3，典型威胁目标［9-10］的RCS 见表4。

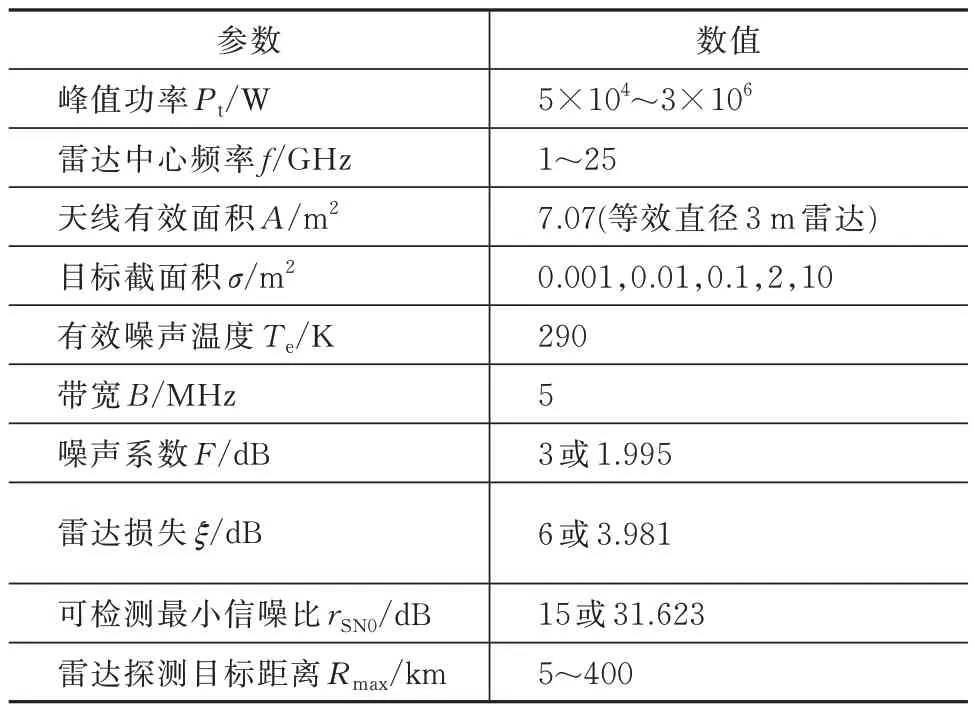
表3 典型雷达参数Tab.3 Parameters of a typical radar

表4 典型威胁目标的RCSTab.4 RCS values of typical threat targets

经计算分析，对于发射功率为60 kW 的X 频段（中心频率为10 GHz）雷达，对应目标截面积分别为0.001、0.01、0.1、2、10 m2时：1）探测距离分别为15、27、48、101、151 km；2）若需实现250 km 的探测，雷达可检测最小信噪比应分别达到-34.0、-24.0、-14.0、-0.7、6.3 dB；3）当发射功率为2.25 MW时，雷达可探测距离分别为37.5、66.7、118.6、250.8、375.1 km。不同目标截面积下，雷达可探性与影响因素关系如图4 所示。

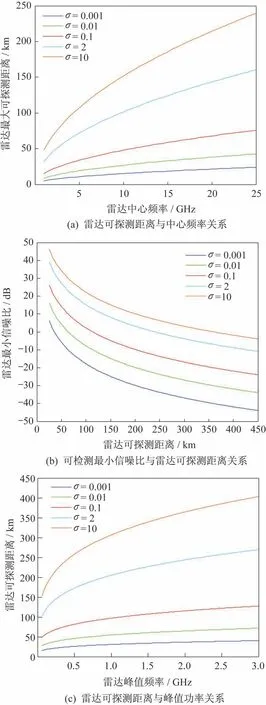
图4 不同目标截面积下，雷达可探性与影响因素关系Fig.4 Relationships of radar detectability and influence factors under different σ

3 威胁目标的可防御性分析

防空武器系统要实现对威胁目标的防御，防御武器［11］的火力拦截备战时间须快于目标穿透防区的时间，满足拦截时间（准备+飞行）小于目标穿透时间的“时间窗口准则”。

防御体系通常采用多层防御拦截，以其中第N层的拦截区为例，将空间关系投影到地平面，如图5所示。第N层防御的火力交战区的近界和远界分别为R1、R2，预警探测区远界为R3；目标相对地面平均飞行速度为Vt；拦截导弹相对地面平均飞行速度为Vm；从预警探测到拦截起飞准备时间为ΔT。

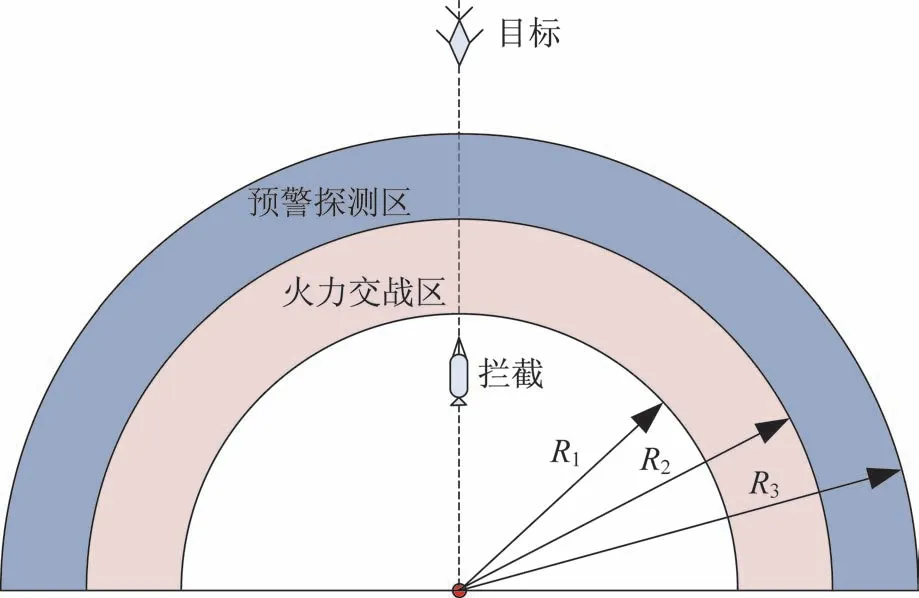
图5 预警探测区、火力交战区示意图Fig.5 Schematic diagram of early warning detection area and firepower engagement area

以目标进入预警探测区远界时刻为起始时间，则有如下关系：

1）目标穿透预警探测区时间为

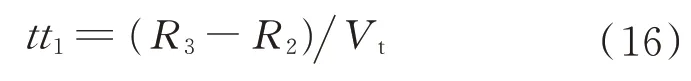
2）目标穿透预警区和交战区总时间为

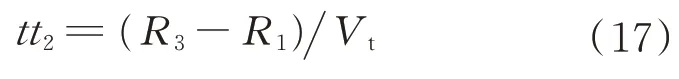
3）拦截弹起飞至飞达交战区近界时间为

4）拦截弹起飞至飞达交战区远界时间为

拦截弹应在交战区完成拦截任务，因此需同时满足：

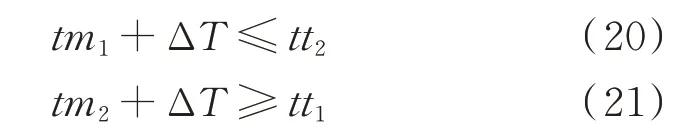
或者

将上述关系式代入不等式有

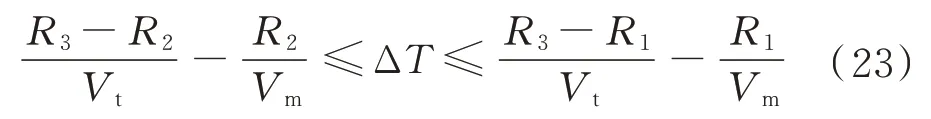
或

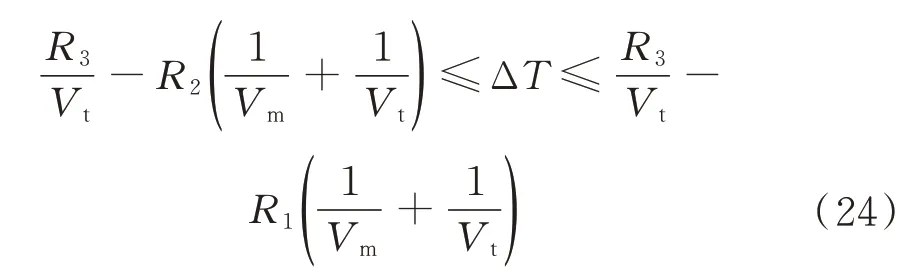
定义1/2 调合平均速度为

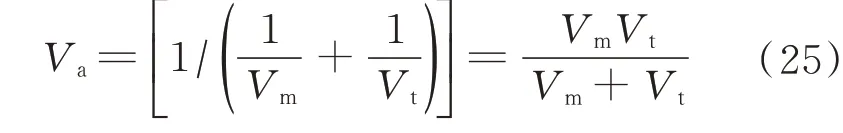
有

下面利用式（26）对分层拦截体系的预警探测区和火力交战区的配置情况进行规划分析。若ΔT、Vt、Vm已知，为避免预警能力不足，目标穿透R1，由tm1+ΔT≤tt2，预警探测远界R3，min应满足

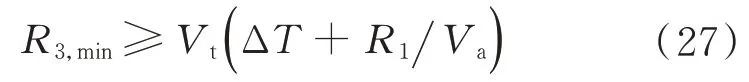
为避免预警能力过剩，以致拦截弹飞达R2后，目标还未到达火力交战区。由tm2+ΔT≥tt1，R3，min应满足

利用上述模型，可对防御武器系统的能力进行初步分析规划和迭代优化，直至满足需求为止。

下面举例进行说明，以中近程防空武器系统为例，拦截实施的步骤如下：

步骤1分析作战威胁目标，确定其运动和电磁特性，见表5。表中，σ为电磁反射特性，Vt、Ht分别为目标平均飞行速度和典型巡航高度.

步骤2规划武器系统的基准能力。武器系统中，ΔT=12 s，Vm=650 m/s，R1=5 km，R2=40 km，R3=100 km（对雷达反射截面积为2 m2的高空常规飞机目标的探测距离）。

步骤3分析传感器对各类目标的可探测距离远界R3。因σ=2 m2时，探测距离为100 km，依据式（14）可得到其他各类目标的可探测距离。

步骤4对于不同飞行速度的威胁目标，分别确定雷达需要的最小探测远界和最大探测远界，从而分析武器系统能力匹配性。若由传感器可观性/可探性确定的探测距离小于或接近需要的最小探测远界，表明武器系统对这类目标不具有防御能力，即存在能力差距；若可观/可探距离均大于最大探测远界，则武器系统存在能力过剩。

由式（27）和式（28）确定防御各类威胁目标所需要的最大、最小探测远界，如表5 和图6（a）所示。

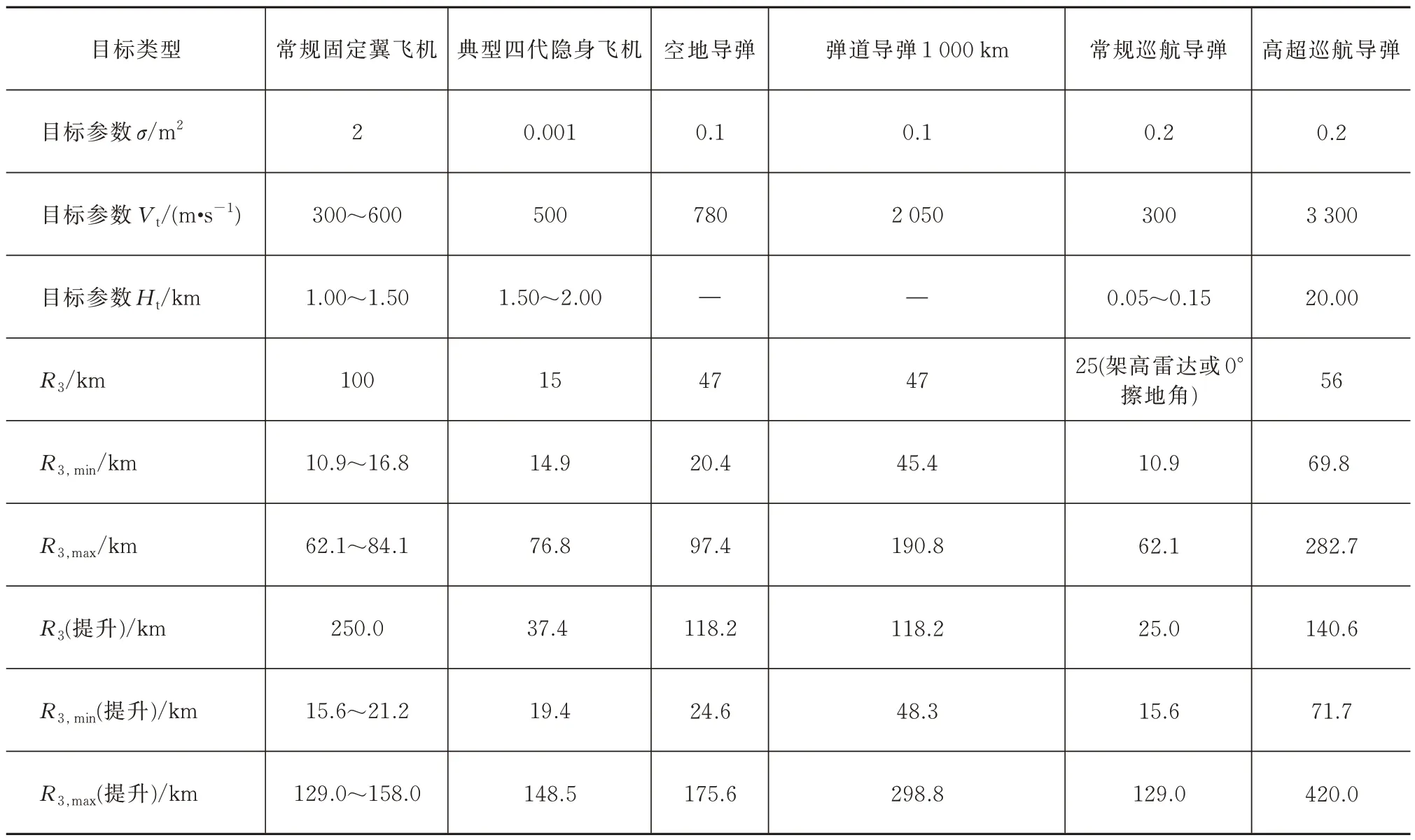
表5 典型防空目标的应对空域范围Tab.5 Response ranges of typical anti-air targets

表5 表明，原规划的武器系统存在能力需求的差距，具体为：1）对常规飞机目标，100 km＞（10.9～16.8）km，能力匹配；2）对隐身飞机目标，15.0～14.9 km，处于临界状态，能力不匹配；3）对空地导弹目标，47.0＞20.4 km，能力匹配；4）对弹道导弹目标，47.0～45.4 km，处于临界状态，能力不匹配；5）对低空巡航弹目标，25.0＞10.9 km，能力匹配，但需要架高雷达或以0°擦地角探测；6）对高超巡航弹目标，56.0＜69.8 km，能力不匹配。

每种威胁目标的速度范围和传感器实际可探测距离如图6 所示。

步骤5对存在能力差距的系统，重新规划系统能力，再进行分析，直到满足能力需求为止。例如，将交战区远界提升2.5 倍，交战区从（5 km，40 km）扩展到（10 km，100 km），将基准预警探测能力也提升2.5 倍，从100 km 提升到250 km；同时，提高拦截弹平均速度1 150 m/s，缩短作战准备时间到10 s。再进行分析计算，如表5 和图6（b）所示。由表5 可知，重新规划之后，武器系统能够对所有威胁目标实施有效防御。

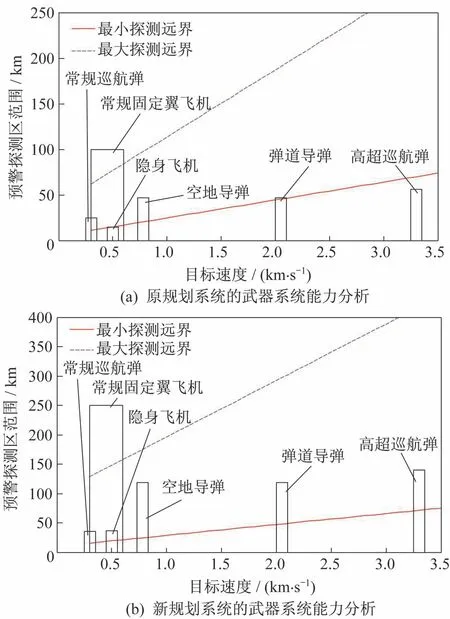
图6 武器系统能力分析Fig.6 Weapon system capability analysis

4 结束语

本文研究并建立了威胁目标、探测传感器、拦截导弹的物理数学简化模型，推导了传感器的可观测性和可探测性条件，得到以下结论：

1）对于低空目标，需要重点考虑地球曲率对雷达可视的遮挡影响。

2）对于主动探测雷达，雷达峰值功率Pt、天线有效截面积A、中心频率f和目标截面积σ越大，雷达可探测距离就越远；反之，噪声温度Te、带宽Bn、噪声系数Fn、系统与传输损失ξ、可识别最低信噪比rSN0增大，会减少雷达可探测距离。

3）主动雷达可探测距离与目标截面积1/4 次方成正比，影响可探测距离的是可检测最小信噪比。

4）应对隐身目标的探测有两类方法：方法1，通过增加雷达峰值功率Pt，或者天线有效截面积A，或者中心频率f，可实现远距隐身目标的探测；方法2，隐身目标并非全频段隐身，对应低频VHF/UHF 频段，其雷达反射截面积较大，可实现探测。对中近程防空武器系统分析实例表明，为应对更多的新威胁目标，武器系统应增大预警探测远界，缩短武器OODA 响应时间，提升导弹飞行速度，拓展交战区范围。本文所介绍的方法可以对防空反导系统的目标可观测性、可探性、可防御性，提供系统有效的建模分析以及方案优化途径。