基于改进BP神经网络的雷达剩余杂波抑制方法

施端阳,林 强,胡 冰,陈 蕾

(1.空军预警学院，武汉 430019；2.中国人民解放军95174部队，武汉 430040)

1 引言

由于雷达工作环境的复杂性，雷达回波信号中包含大量的地物、气象、海洋等杂波和各种干扰。传统的信号处理技术，如动目标显示、动目标检测和恒虚警率等，对雷达回波信号进行检测后，不能完全滤除杂波，仍会存在大量的剩余杂波。这些剩余杂波不仅会形成虚假点迹，影响航迹的质量，还可能会导致数据处理系统饱和，影响雷达探测性能的发挥。因此，对信号处理后的剩余杂波进行有效抑制具有重要的研究意义。

目前，国内外对剩余杂波抑制方法的研究取得了一些成果。文献[1]提出了基于AdaBoost的雷达剩余杂波抑制方法，该方法运用自适应提升算法构造决策树分类器，通过组合多个基学习器的结果对目标和杂波进行分类，解决了弱学习器在特征不明显的杂波点迹上表现不佳的问题。文献[2]提出了一种基于径向基神经网络的海杂波抑制方法，通过改进的IGWO算法进行优化，解决了GWO算法收敛速度慢，易陷入局部优化的不足，对海杂波具有较好的抑制作用。文献[3]针对复杂天气条件下，气象雷达杂波抑制效果差的问题，提出了一种基于模糊神经网络的杂波抑制方法，利用神经网络训练得到地杂波各极化参数的隶属函数，该方法的识别结果更符合地杂波宽分布和非均匀分布的特性，对地杂波抑制起到了较好的效果。文献[4]综合考虑了目标与杂波在幅度、相位、距离等特征的差异，利用综合特征因子评估过滤杂波，降低了虚假航迹率和点迹损失率。但该方法在综合特征因子求取时，加权因子的确定依赖经验值，影响了算法的运算效率和杂波抑制效果。文献[5]提出了一种基于杂波图的杂波抑制方法，分别对单部雷达和组网雷达进行杂波抑制。但该方法需要对杂波区域进行判别、划分，根据不同杂波区选取不同的判别门限，在组网时要考虑不同雷达的融合权值，计算过程较为复杂。文献[6]在研究了雷达信号处理中的动目标显示和动目标检测2种杂波抑制技术的基础上，应用了K近邻算法对目标和杂波进行判别，但是该方法的杂波剩余点迹抑制率不到70%，杂波点迹识别率还有待提高。文献[7]设计了5层BP神经网络分类器，采用L-M算法对分类器进行训练，较K近邻算法和支持向量机提高了分类精度。但是该方法的神经网络过于复杂，识别时间较长，不太适用于雷达剩余杂波的快速识别。

本文针对现有BP神经网络算法学习速度慢，杂波识别率较低的问题，提出了一种改进的BP神经网络抑制杂波的方法。选取多普勒速度、目标原始幅度、杂噪比等8个特征作为输入，设计雷达点迹分类器，引入弹性BP算法提高神经网络的收敛速度，并对网络结构进行优化。结果表明，改进后的BP神经网络算法既节省了识别时间，也提升了杂波抑制的效果。

2 BP神经网络

BP神经网络是一种由输入层、隐含层和输出层组成的多层前馈网络[8-9]。BP神经网络的隐含层数量和各层的节点数可以是一个或者多个，一个包含单个隐含层的BP神经网络可以实现M维到N维的非线性映射，如图1所示[10]。

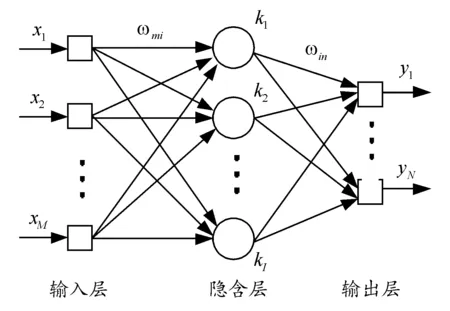
图1 BP神经网络示意图

BP神经网络各层之间全连接，同一层的神经元相互不连接。在BP神经网络中，数据按照输入层-隐含层-输出层的顺序，逐层向后传播。在对网络的权值进行训练时，沿着误差减小的方向，按照反向顺序，逐层向前修正权值，通过多次的学习训练，最终的误差逐渐缩小至符合要求的范围，此时神经网络训练完成。

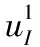
(1)

网络的期望输出为：

d(s)=[d1,d2,…,dJ]

(2)

2.1 工作信号正向传播

神经网络中输入层的节点数为输入向量的维数，输入层的输出为神经网络的输入信号。假设输入信号为x(s)，则输入层第m个神经元的输出为：

(3)

隐含层第i个神经元的输入为：

(4)

假设隐含层传递函数为f(·)，则隐含层第i个神经元的输出为：

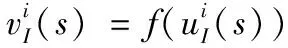
(5)

输出层第n个神经元的输入为：

(6)

假设输出层传递函数为g(·)，则输出层第n个神经元的输出为：

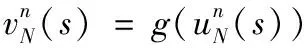
(7)

输出层第n个神经元的误差为：

(8)

神经网络的总误差为：

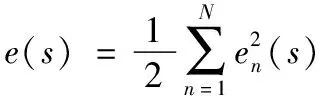
(9)

2.2 误差信号反向传播

神经网络在调整权值时，按照网络逐层反向调整。隐含层与输出层之间的权值调整为：

ωin(s+1)=ωin(s)+Δωin(s)

(10)

输入层与隐含层之间的权值调整为：

ωmi(s+1)=ωmi(s)+Δωmi(s)

(11)

式中，Δωin(s)、Δωmi(s)分别为隐含层与输出层之间和输入层与隐含层之间的权值调整量，其大小取决于训练算法。

3 改进前后的BP神经网络模型

BP神经网络包含训练和学习2个过程[11]。网络训练时，数据通过输入层进入网络，然后传递至隐含层各神经元，数据经过传递函数变换后传递到输出层输出。当实际输出值与期望值误差较大时，误差反向经过隐含层传递到输入层，传递时将误差分配至每一层，各层的神经元权值根据误差进行调整，直至满足训练停止条件。网络学习时，先对网络进行初始化设置，分配连接权值，确定学习次数、误差函数。然后输入训练数据，计算隐含层的输入输出，调整权值。最后计算全局误差，直至误差满足停止条件[12]。

BP神经网络的设计包含网络层数、输入层节点数、隐含层节点数、输出层节点数、传递函数、训练方法和训练参数设置等内容[13]。

3.1 经典BP神经网络模型

1)网络层数

BP神经网络包含一个或多个隐含层。文献[7]中构建了5层神经网络，其中包含一个输入层、3个隐含层和一个输出层。

2)输入层节点数

输入层的节点数取决于输入数据的维数。文献[7]中选取的数据特征为方位、距离、信噪比、幅度、方位跨度和距离跨度等6维特征，因此输入层节点数为6个。

3)隐含层节点数

文献[7]中第1个隐含层有10个节点，第2个隐含层有20个节点，第3个隐含层有10个节点。

4)输出层节点数

输出层的节点数取决于输出数据的维数。在雷达剩余杂波抑制的过程中，需要根据BP神经网络来识别雷达点迹为目标还是杂波，输出数据为一维数据，因此输出层节点数为1个。

5)传递函数和训练参数

BP神经网络的传递函数必须可微[14]。文献[7]中隐含层传递函数为tansig函数，输出层为logsig函数。

6)训练方法

标准BP神经网络的训练算法为最速下降法，但该算法的收敛速度慢，易陷入局部极小。文献[7]中采用了L-M算法，使训练速度得到了一定的提升。

3.2 本文改进BP神经网络模型

1)网络层数

文献[7]中构建的网络结构过于复杂，导致雷达点迹判别耗时较长，无法快速抑制杂波。经理论证实，单个隐含层结构的网络可以实现任意非线性映射[15]。因此，本文构建了3层BP神经网络，包含一个输入层、一个隐含层和一个输出层，简化了网络结构，提高了模型的识别速度。

2)输入层节点数

本文选取的数据特征为多普勒速度、目标原始幅度、目标背景幅度、滤波标志、恒虚警类型、杂噪比、滤波器组选择和EP质量等8维特征，因此输入层节点数为8个。

3)隐含层节点数

隐含层的节点数对BP神经网络的性能影响巨大，隐含层节点数增多可以提高网络的性能，但也会延长训练时间。文献[7]中设计隐含层节点数时未给出设计的依据，存在一定的随意性。本文隐含层节点数采取下式确定：

(12)

式中，M和N分别为输入层和输出层节点数，a是[0,10]之间的常数。本文中输入层和输出层节点数分别为8个和1个，a取值为10，因此隐含层节点数为13个。

4)输出层节点数

本文中，网络输出为0或1的一维数据，0代表该雷达点迹识别为杂波，1代表该雷达点迹识别为目标，因此输出层节点数为1个。

5)传递函数和训练参数

本文选用Tan-Sigmoid函数为隐含层传递函数，线性函数purelin函数为输出层传递函数。网络学习率为0.01，目标误差为10-7，最大迭代次数为1 000次。

6)训练方法

文献[7]中采用了L-M算法，模型的识别时间仍然较长，识别率较低。本文引入弹性BP算法，以提高神经网络的训练速度和识别率。弹性BP算法在调整权值时，仅使用了偏导的符号，而未使用偏导的幅值，这样权值的调整量就与幅值无关，可消除梯度幅度的不良影响。权值调整量的大小由下式决定：

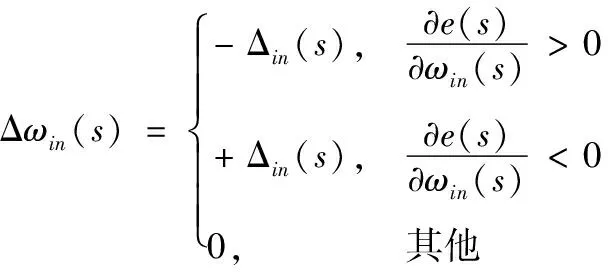
(13)

权值的调整遵循以下原则，如果偏导为正，则权值减小，如果偏导为负，则权值增加。下一次迭代的权值调整量为：

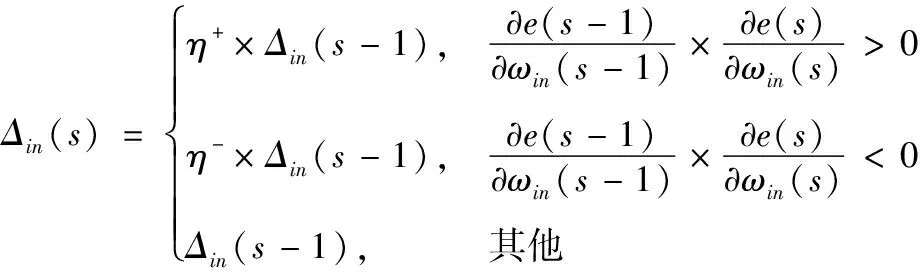
(14)

式中，Δin(s)为权值的调整步长，Δin(s)∈[Δmin,Δmax]，0<η-<1<η+为调整系数。

与以学习率为基础的其他算法不同的是，弹性BP算法直接修改调整权值，因此不会导致因为无法预期的梯度变化而使修改后的网络性能下降。当训练发生振荡时，弹性BP算法的权值调整量将减小，在多次迭代中权值朝相同方向变化时，权值调整量增大。因此，弹性BP算法的收敛速度更快。

3.3 BP神经网络训练与分类

将雷达点迹训练数据输入设计好的BP神经网络中进行训练，当分类精度满足要求时，网络训练完成。将雷达点迹测试数据输入训练好的网络中，通过输出识别雷达点迹为目标还是杂波，若识别为杂波，则滤除该点迹，以达到抑制杂波的目的。

文中所提雷达剩余杂波抑制方法的流程如图2所示。

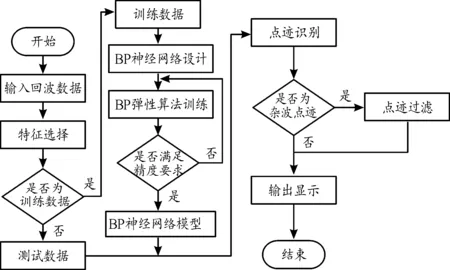
图2 基于BP神经网络的雷达剩余杂波抑制流程框图

4 实验结果与分析

采集某型空管雷达的30 000个点迹实测数据，选取24 000个作为训练样本，其中目标点迹和杂波点迹各12 000个，剩余6 000个作为测试样本，其中目标点迹和杂波点迹各3 000个。数据分布如表1所示。

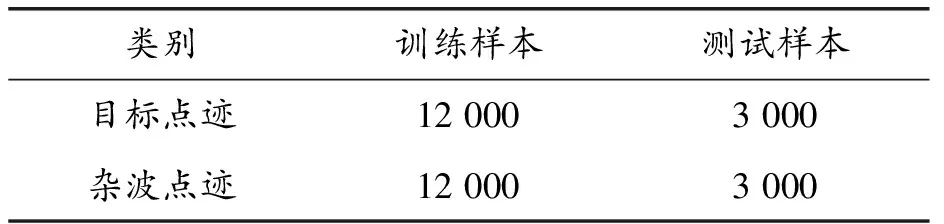
表1 数据分布

实验内容分为2个部分，实验1通过设计的BP神经网络测试不同特征组合时的雷达点迹识别率，选取最优的特征组合作为点迹识别模型的输入数据；实验2将本文提出的方法与文献[7]中的方法进行对比分析。

4.1 最优特征组合的选取

从采集的雷达点迹特征中选取8个特征进行测试，分别为：多普勒速度、目标原始幅度、目标背景幅度、滤波标志、恒虚警类型、杂噪比、滤波器组选择和EP质量。对单个特征或者多个特征组合时BP神经网络模型的识别率进行研究，不同特征下的识别率如表2所示。

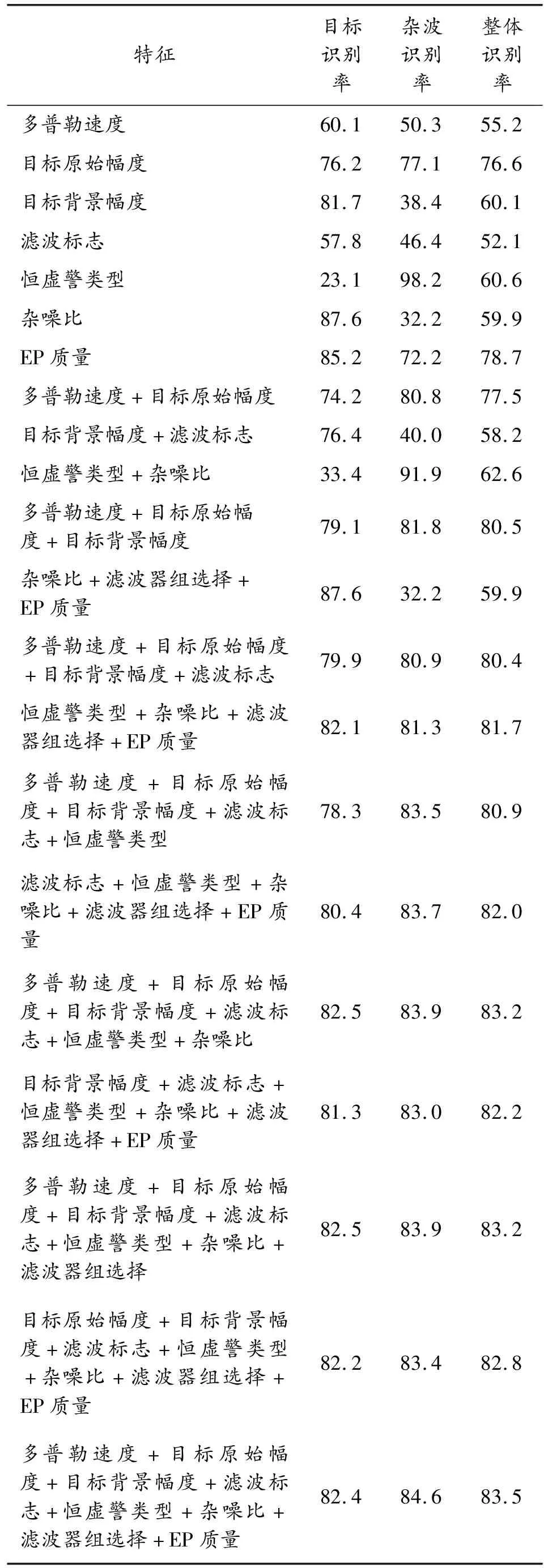
表2 不同特征下的识别率(%)

由表2可知，在特征组合为“多普勒速度+目标原始幅度+目标背景幅度+滤波标志+恒虚警类型+杂噪比+滤波器组选择+EP质量”时模型的识别率最高，目标识别率为82.4%，杂波识别率为84.6%，整体识别率为83.5%。因此，该组合为最优特征组合。

4.2 2种方法对比

由最优特征组合中特征的数量可知，BP神经网络的输入数据维数为8维，因此输入层节点数为8个。已知输出层节点数为1，由式(12)可知，隐含层节点数范围为[3,13]。经过验证，隐含层节点为13时的效果最好。因此，本文的BP神经网络由8个节点的输入层、13个节点的隐含层和1个节点的输出层构成。如图3所示，本文设计的神经网络结构比文献[7]中的神经网络更加简单。

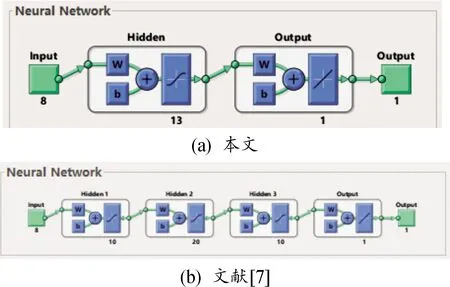
图3 2种BP神经网络结构示意图

为了对比2种BP神经网络的识别时间和杂波抑制效果，采取相同的训练数据对2种BP神经网络进行训练，利用相同的测试数据对训练好的模型分别进行测试，得到的识别时间如图4所示，均方误差如图5所示。

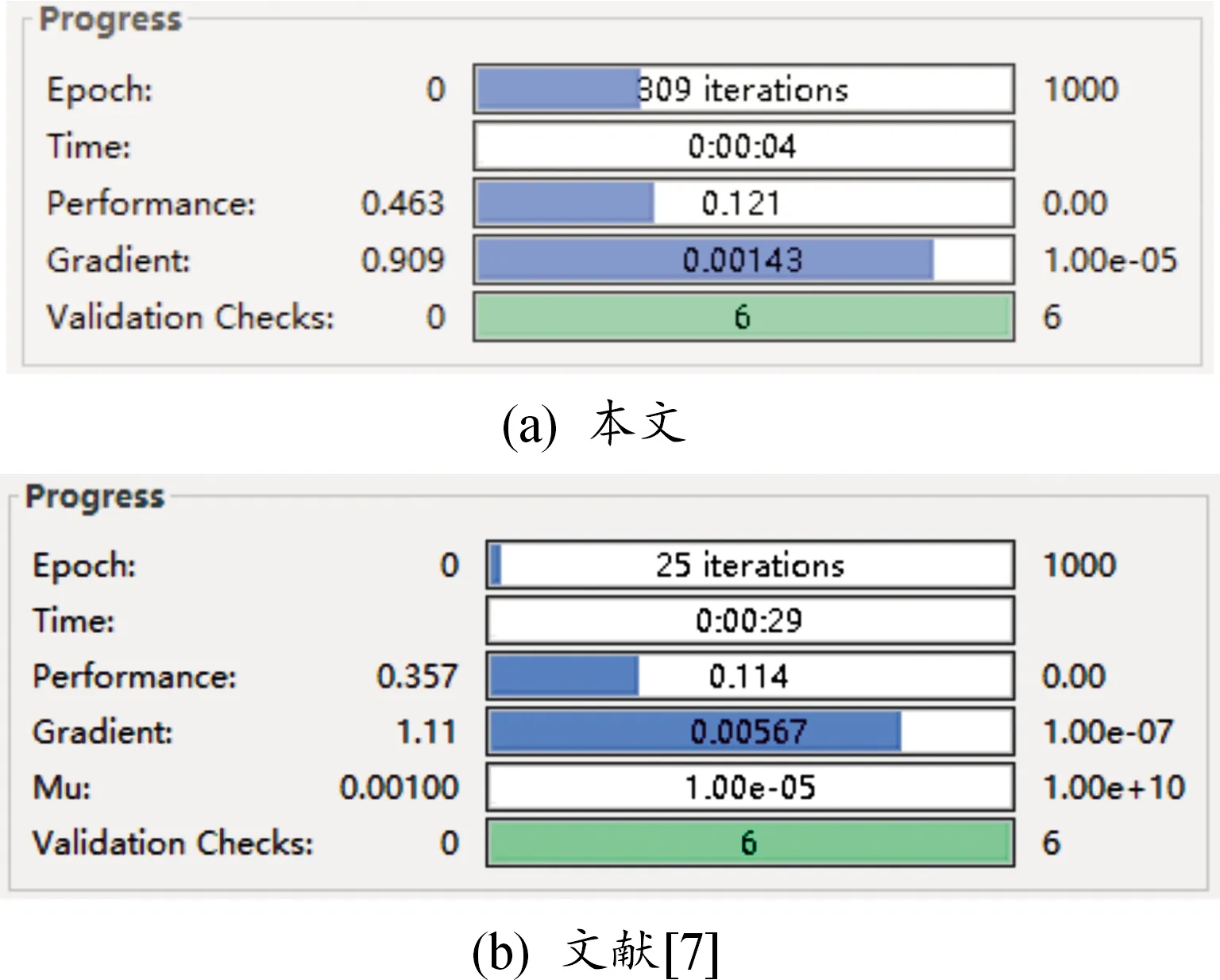
图4 2种BP神经网络结构识别时间界面

从图4中可以看出，本文方法BP神经网络识别时间为4 s，文献[7]中BP神经网络的识别时间为29 s，前者比后者的识别时间节省了86%。从图5中可以看出，本文方法神经网络在迭代303次时均方误差最低，误差为0.117 49，文献[7]中BP神经网络在迭代19次时的均方误差最低，误差为0.121 21，前者在更短的时间内迭代次数更多且误差下降更快最优误差更小。通过图4和图5可以说明，本文方法收敛速度更快，精度更高，显著提高了雷达点迹识别的效率，在雷达这种对情报实时性要求较高的装备中，本文方法具有更好的适用性。

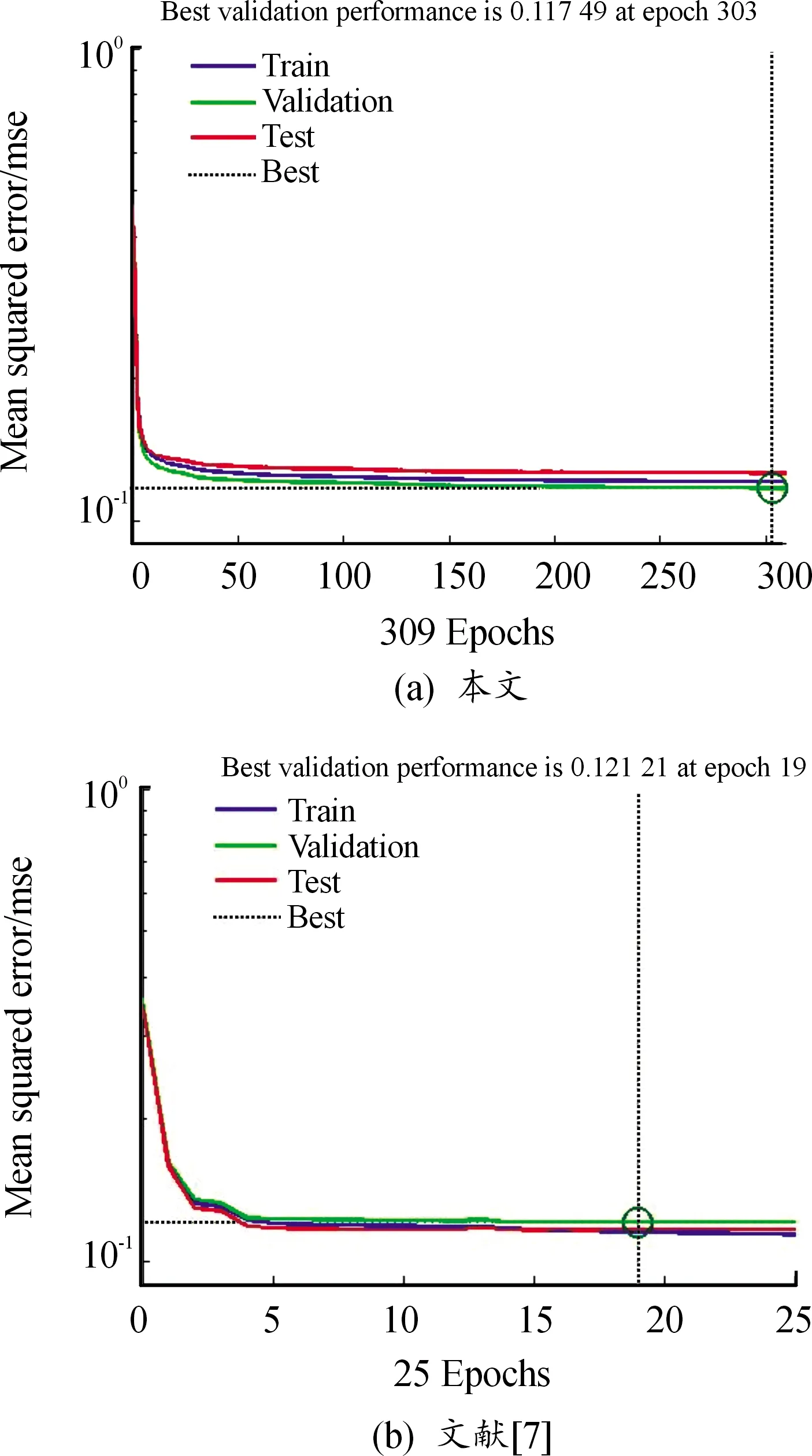
图5 2种BP神经网络均方误差曲线

图6为3 000个测试样本在分类识别前的分布图，横坐标为方位，纵坐标为距离，绿色点代表目标点迹，红色点代表杂波点迹。

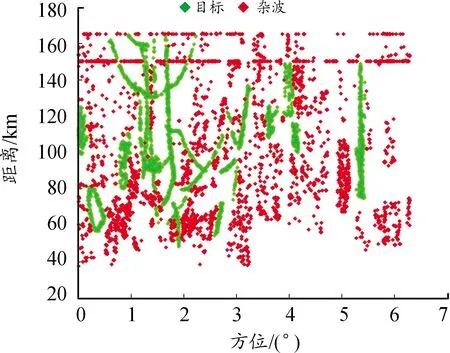
图6 测试样本空间分布图

图7为采取2种BP神经网络杂波抑制后的效果图，前者为本文方法杂波抑制后的效果，后者为文献[7]中方法杂波抑制后的效果。从图6和图7的对比中可以看出，采取2种BP神经网络后大部分杂波都被成功抑制。从图7可以看出，在圆框内的区域中，本文方法剩余的杂波点迹更少，杂波抑制的效果更好。

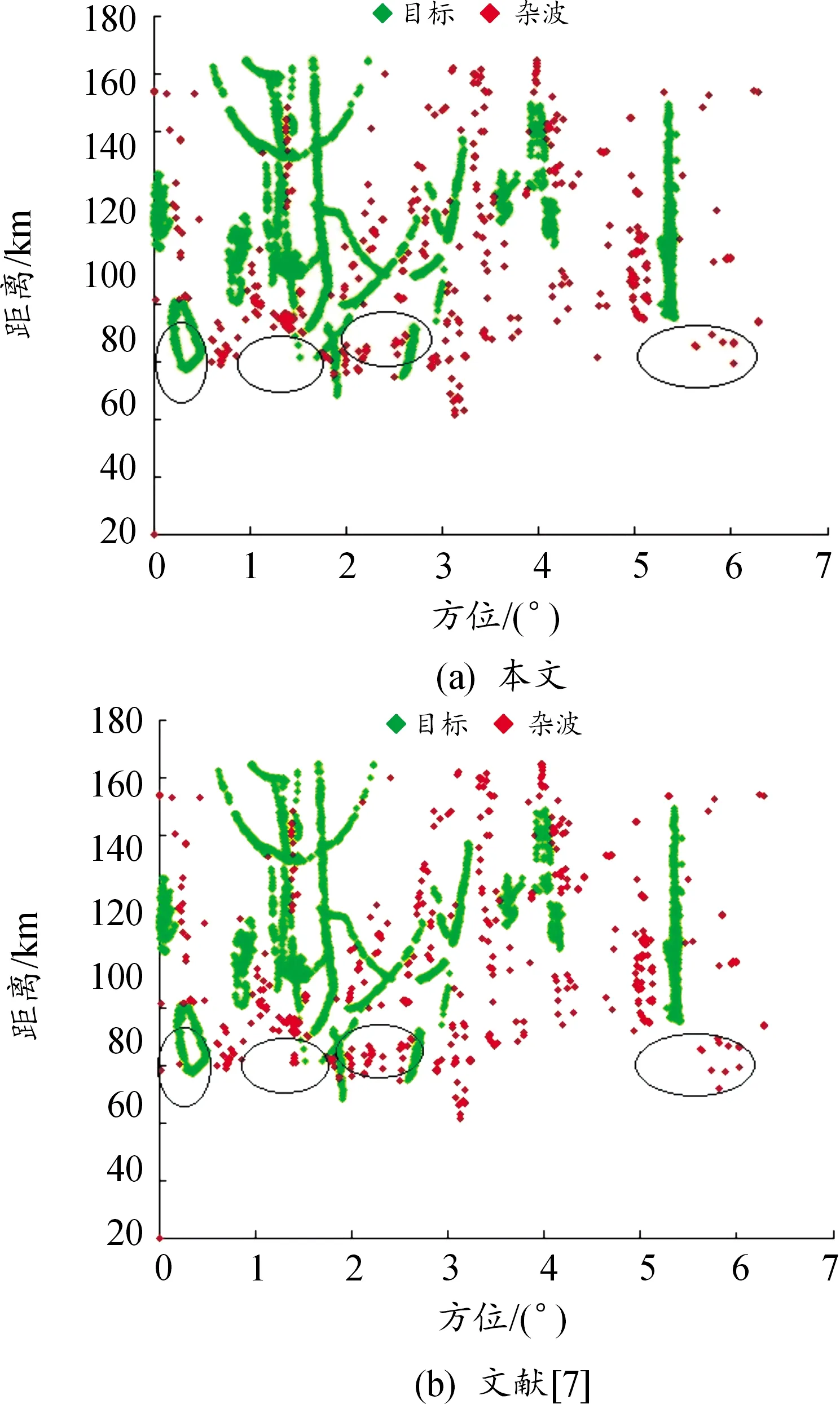
图7 2种方法杂波抑制效果图

2种方法的识别率如表3所示。由表3可知，本文方法比文献[7]中方法杂波点迹识别率提升了1.6%，整体点迹识别率提升了0.2%，识别精度更高，杂波抑制效果更好。

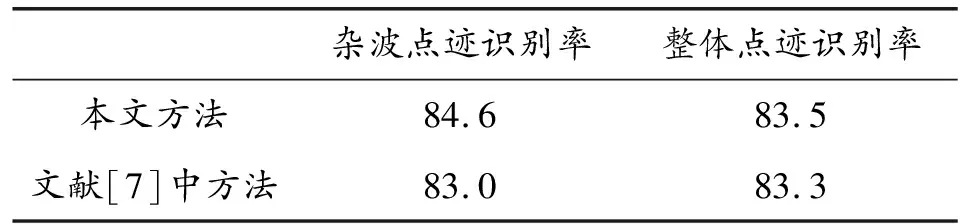
表3 2种方法的识别率(%)

5 结论

本文引入弹性BP算法，改进现有的BP神经网络训练算法，提升了网络收敛速度。通过分析隐含层的层数和节点数，减少了现有神经网络中隐含层层数和节点数的数量，简化了BP神经网络的结构，提高了雷达点迹识别率。通过计算雷达实测数据，证明本文提出的雷达剩余杂波抑制方法，不仅缩短了识别时间，也提高了杂波的抑制效果，对雷达装备在实际工作中快速高效地抑制剩余杂波具有指导作用。