某带减速气囊的航空子弹气动特性研究

陈跃健，王 浩

(南京理工大学 能源与动力工程学院，南京 210094)

1 引言

子母弹是一种包含现代高新技术的复杂武器，其作战过程包括母弹的发射或投放、子弹与母弹的分离抛撒、子弹气动减速飞行等基本过程[1]。亚音速航空子弹在被抛撒之后的大攻角飞行过程中，充气式减速气囊的大钝角锥形结构与气体介质作用可以产生与运动方向相反的气动阻力，以实现子弹的快速减速，该阶段对于子弹后续的目标打击非常重要。航空子弹存在大攻角飞行打开减速系统的过程，飞行状况较为复杂。在相关气动减速弹丸研究中，比较常见的是减速伞结构[2]，但由于其存在非正常姿态导致开伞失败以及不稳定等问题，并不适用于航空子弹的复杂飞行条件。因此需要一种阻力特性和结构强度更好、适应范围更广的自充气式气动减速气囊[3,4]，来实现航空子弹大攻角[5]飞行条件下的减速过程。

当前国内外对飞行器气动特性研究的方法主要是试验和数值模拟。试验的主要方式是风洞和空投，但成本较高且过程复杂。随着计算机技术的发展以及数值模拟技术的趋于成熟，可以较为精确的计算出飞行器的流场分布和气动参数，从而弥补了试验研究的短板。FLUENT可以用来模拟从不可压缩到高度可压缩范围内的复杂流动，由于采用了多种求解方法和多重网格加速收敛技术，可以达到更佳的收敛速度和求解精度[6]。

本文中基于计算流体力学方法，建立带充气式减速气囊的亚音速航空子弹模型，在马赫数为0.4、0.6、0.8，攻角为0°～90°的飞行工况下开展数值模拟，研究带减速气囊的亚音速航空子弹大攻角飞行的气动特性，并对减速效果进行了分析，相关结果可为同种弹型的充气式气动减速研究提供理论参考。

2 控制方程与湍流模型

2.1 RANS方程

可压缩RANS[7-9]方程可以表示成采用求和约定的笛卡尔张量形式，连续方程为

(1)

动量方程为

(2)

(3)

式中：μ为动力黏度，δij为克罗内克张量分量。动量方程式(2)右侧的最后一项代表雷诺应力的梯度，采用Boussinesq涡黏性假设计算雷诺应力

(4)

式中:μt为湍流黏度，k为湍动能。

能量方程为

(5)

其中：H为气体的焓，T为温度，ka为气体热导率，cp为气体比定压热容。对于理性气体

H=cpT

(6)

式中，Prt为湍流普朗特数，包含Prt的项可以视为湍流热导率，(τij)eff为有效应力张量分量。

(7)

式中：μeff为有效黏度，是动力黏度与湍流黏度之和。

2.2 湍流模型

(8)

S-A模型相对于两方程模型计算量小、稳定性好，计算网格在壁面的加密程度与零方程模型有同等的量级。此外，在有多物面的复杂流场计算中不需要特殊处理[11-12]。基于以上特点选用S-A模型。

3 子弹的物理模型与数值方法

3.1 计算物理模型

采用三维软件Solid Edge建立带气囊的子弹的几何模型，其中子弹为圆柱形，充气气囊与子弹形成大钝角锥形结构。子弹长400 mm，直径200 mm，气囊展开直径为600 mm。子弹头部进行了圆弧倒角处理。因弹体对称，计算中采用二分之一模型和对称边界条件，如图1所示。

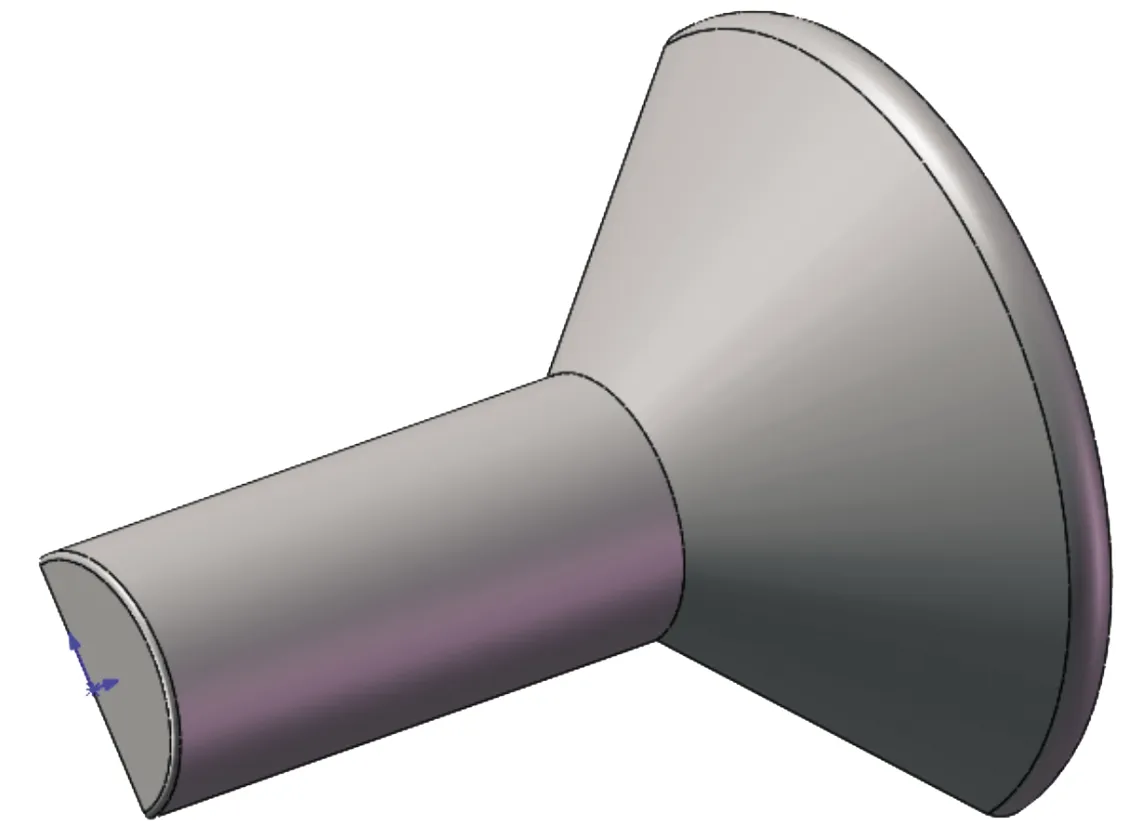
图1 带充气式减速气囊的航空子弹模型示意图

3.2 模型与数值方法验证

针对数值方法验证以及网格无关性验证，以Finner(BFM)国际标准尾翼弹模型为参考模型，此标准模型有较多的实验数据可以做参考[13]。弹径D=100 mm，如图2所示。

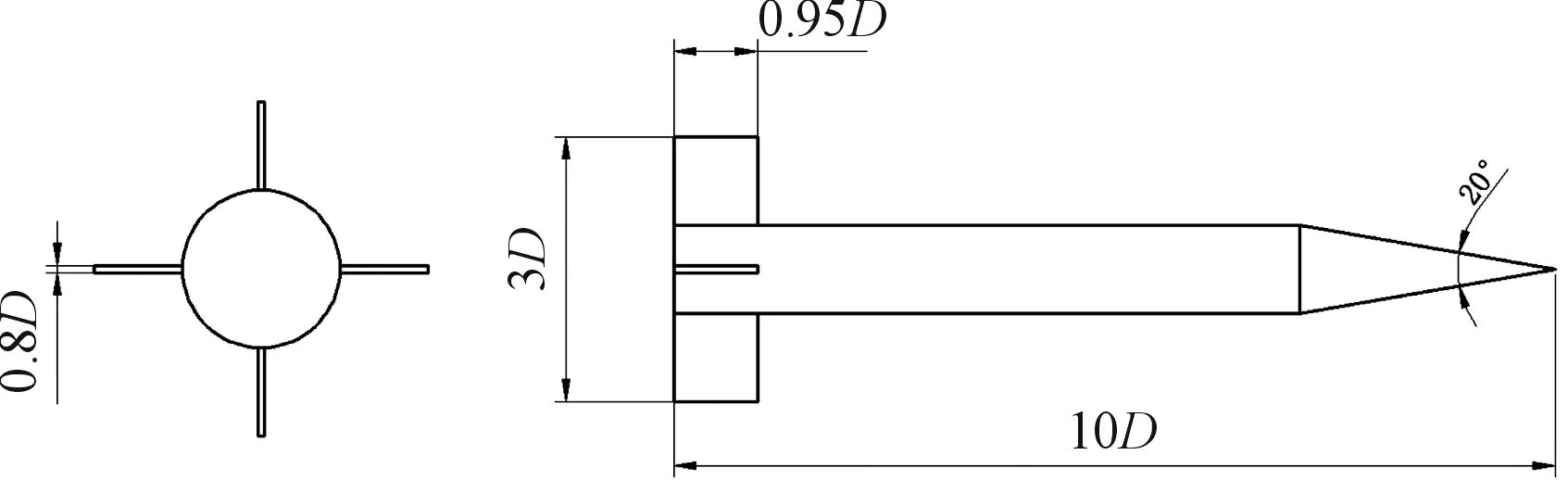
图2 标准尾翼弹模型示意图

当模型网格精度在能够满足仿真计算的要求，并且对结果的可靠性不会造成较大的影响时，对模型的网格数量分别为90万、200万、420万，采用完全相同的计算方式，计算工况来流为0.3Ma，攻角为6°。通过监视器观察收敛情况直至系统计算收敛，得到仿真计算结果，所得的阻力系数、升力系数、俯仰力矩系数与风洞试验值如图3所示。

从图3分析得出，3种不同数量的网格计算所得的阻力系数、升力系数、俯仰力矩系数的值分布差距不大，数量为92万的网格所计算的升力系数结果与420万的网格模型计算的结果相比有明显的偏差，但其相对误差也在15%内，有可能是网格数量太少或者是网格的精度还不够导致的。

因此，考虑计算资源情况下，合理范围内尽可能提高网格数量和网格精度来计算，以便于获得更小的误差。

3.3 计算流场网格

绕流流场的大小设为模型尺寸的10倍左右，满足流场的充分发展。流场采用结构网格划分，弹体表面附近进行网格加密，部分网格划分结果如图4所示，流场边界为压力远场。

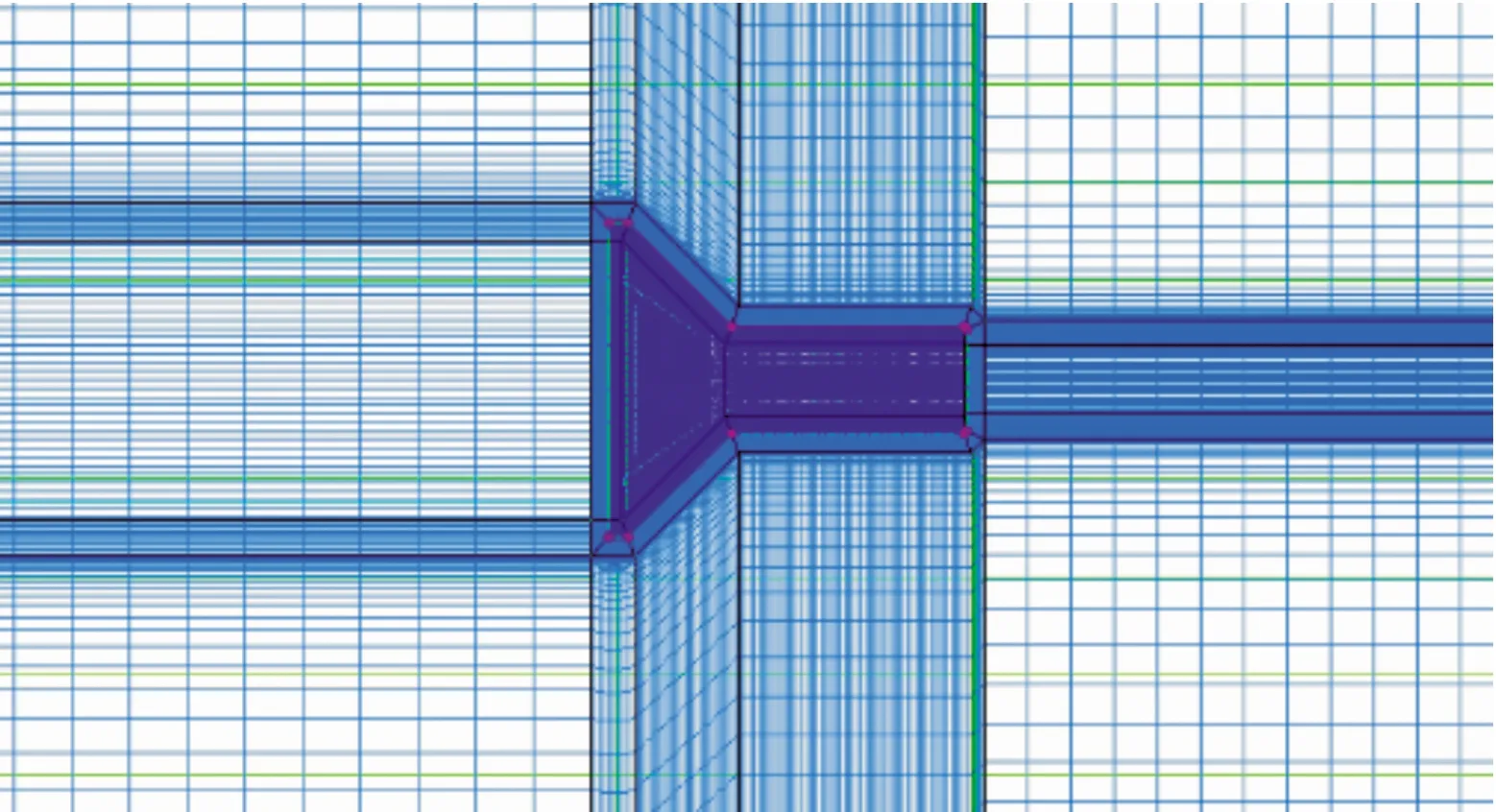
图4 计算域部分网格示意图

对此模型采用相同数值方法并进行网格无关性验证。通过调整网格节点数生成不同数量级的网格，对数量分别为100万、300万、500万的3套网格模型，选择相同的数值方法做相同的设置进行迭代计算，将所得阻力系数进行对比如图5所示。从图中可以看出，100万网格模型计算的结果与其他两网格模型的结果差值稍微明显，考虑到时间与计算资源选用300万网格模型更合理。

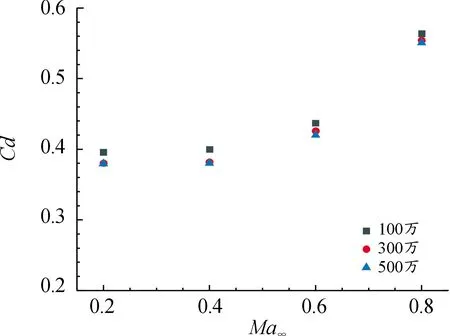
图5 零攻角来流下不同数量的网格模型计算结果示意图

3.4 计算方法[14]

1)将ICEM软件划分的网格导入Fluent中。设置网格尺寸，检查网格质量。

2)选择密度基求解器，湍流模型选择单方程模型。

3)在流体属性设置中，选以理想气体做介质，气体黏度满足萨兰德定理。

4)定义对称面以及边界条件，设置大气压101 325 Pa，参考压力设为0。壁面条件设为无滑移。

5)定义监视器，设置迭代步数进行计算。

4 计算结果与分析

为了研究带充气式减速气囊的子弹的气动特性，计算工况马赫数分别为0.4、0.6、0.8，攻角为0°～90°。在给定攻角和来流马赫数下，各系数随着迭代次数增加不断波动，弹体的气动参数曲线在迭代3 000次慢慢趋于稳定后即可得到气动参数值。图6是阻力系数曲线，图7是升力系数曲线，图8是俯仰力矩系数曲线。曲线趋于收敛可表明系统的设计是较为稳定的。

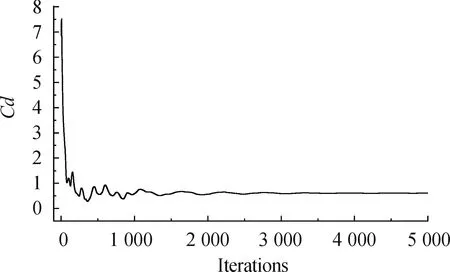
图6 速度0.8Ma，攻角30°时阻力系数曲线

图7 速度0.8Ma，攻角30°时升力系数曲线

图8 速度0.8Ma，攻角30°时俯仰力矩系数曲线

4.1 阻力特性

在攻角为0°～90°、马赫数分别为0.4、0.6、0.8工况下得到阻力系数曲线如图9。

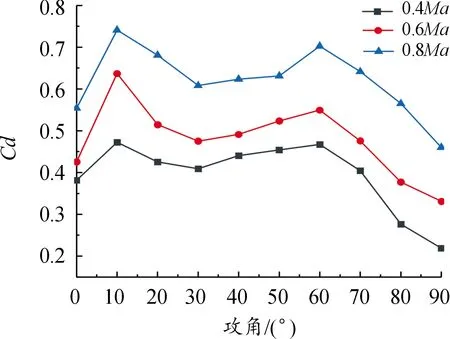
图9 不同马赫数不同攻角的子弹阻力系数曲线

从图9可以发现，来流攻角相同条件下，子弹的阻力系数随着来流马赫数的增加而增大。来流马赫数相同条件下，子弹的阻力系数随着攻角的变化呈现相同的变化趋势，攻角为0°～10°、30°～60°时，阻力系数与其正相关，在10°～30°、60°～90°与其负相关，且在攻角大于60°时，阻力系数急剧下降。

4.2 升力特性

在攻角为0°～90°、马赫数分别为0.4、0.6、0.8工况下得到升力系数曲线如图10。

从图10可以发现，来流攻角相同条件下，来流速度对子弹的升力系数影响较小；在攻角为0°～10°、20°～40°时，子弹的升力系数随着攻角的增大而增大；来流马赫数相同条件下，子弹升力系数的变化随着攻角的变化呈现相同的趋势，在攻角大于50°时，升力系数急剧下降，攻角在大于55°左右，升力系数始终为负值。

4.3 俯仰力矩特性

在攻角为0°～90°、马赫数分别为0.4、0.6、0.8工况下得到俯仰力矩系数曲线如图11。

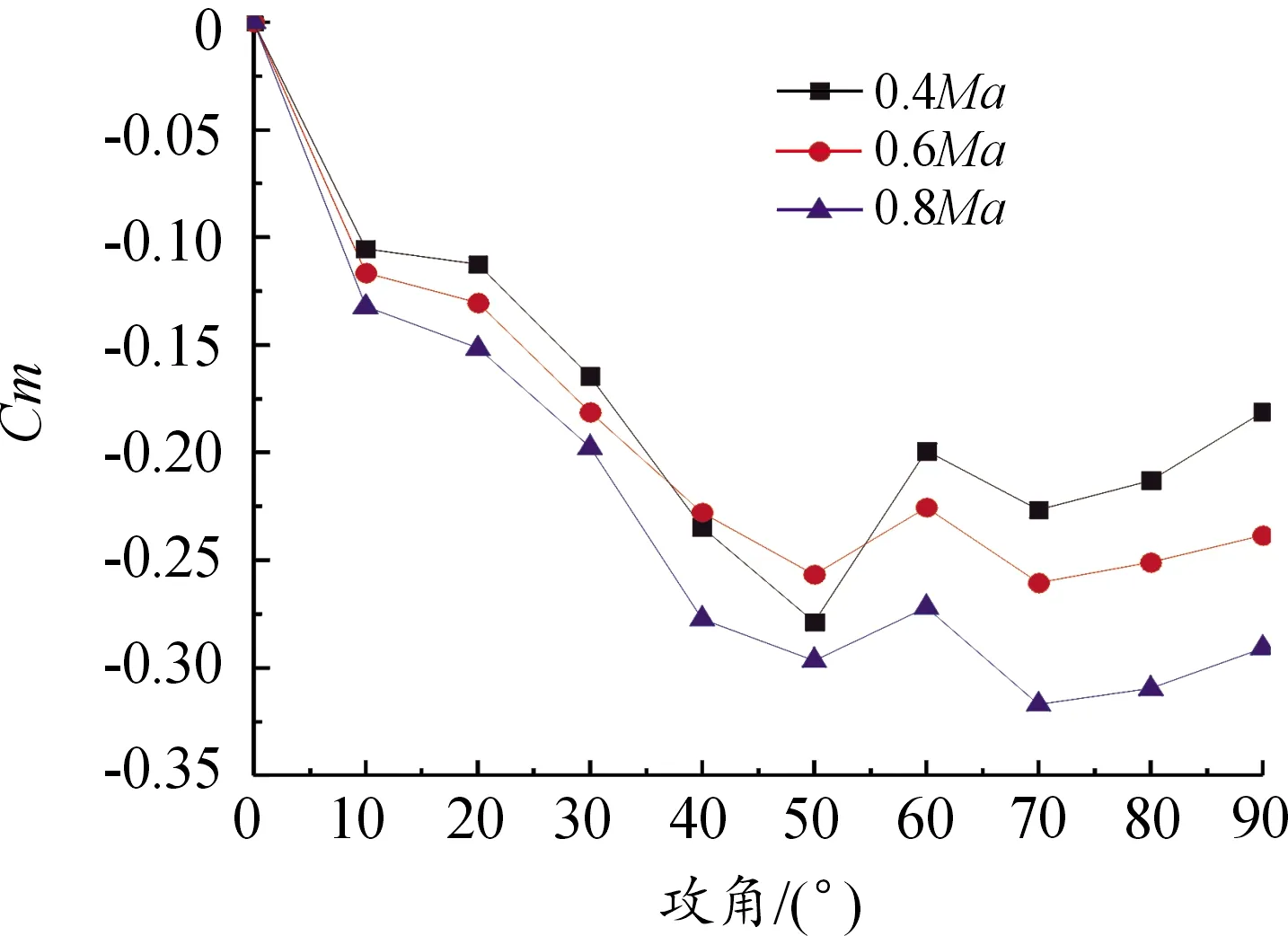
图11 不同马赫数不同攻角的子弹俯仰力矩系数曲线

从图11可以看出，子弹的俯仰力矩系数为负，具有好的静稳定性；攻角在0°～50°内，负向俯仰力矩随着攻角的增大逐渐增大，50°～90°变化幅度较小。来流马赫数相同条件下，子弹的俯仰力矩系数变化随着攻角的变化呈现相同的趋势。

4.4 减速效果验证和飞行稳定性分析

基于无控六自由度刚体弹道方程，具体方程组形式以及各变量参数参见文献[15]，对带减速气囊的子弹模型进行弹道仿真。假设子弹竖直方向牵连速度为300 m/s，子弹轴向横抛速度15 m/s，得到子弹速度曲线如图12所示，可以发现，3 s内子弹速度由300 m/s降到83 m/s内，充气式减速气囊的减速效果比较理想。子弹攻角曲线如图13所示，从图中可以看出子弹的攻角能够较快的收敛，最后趋于稳定。

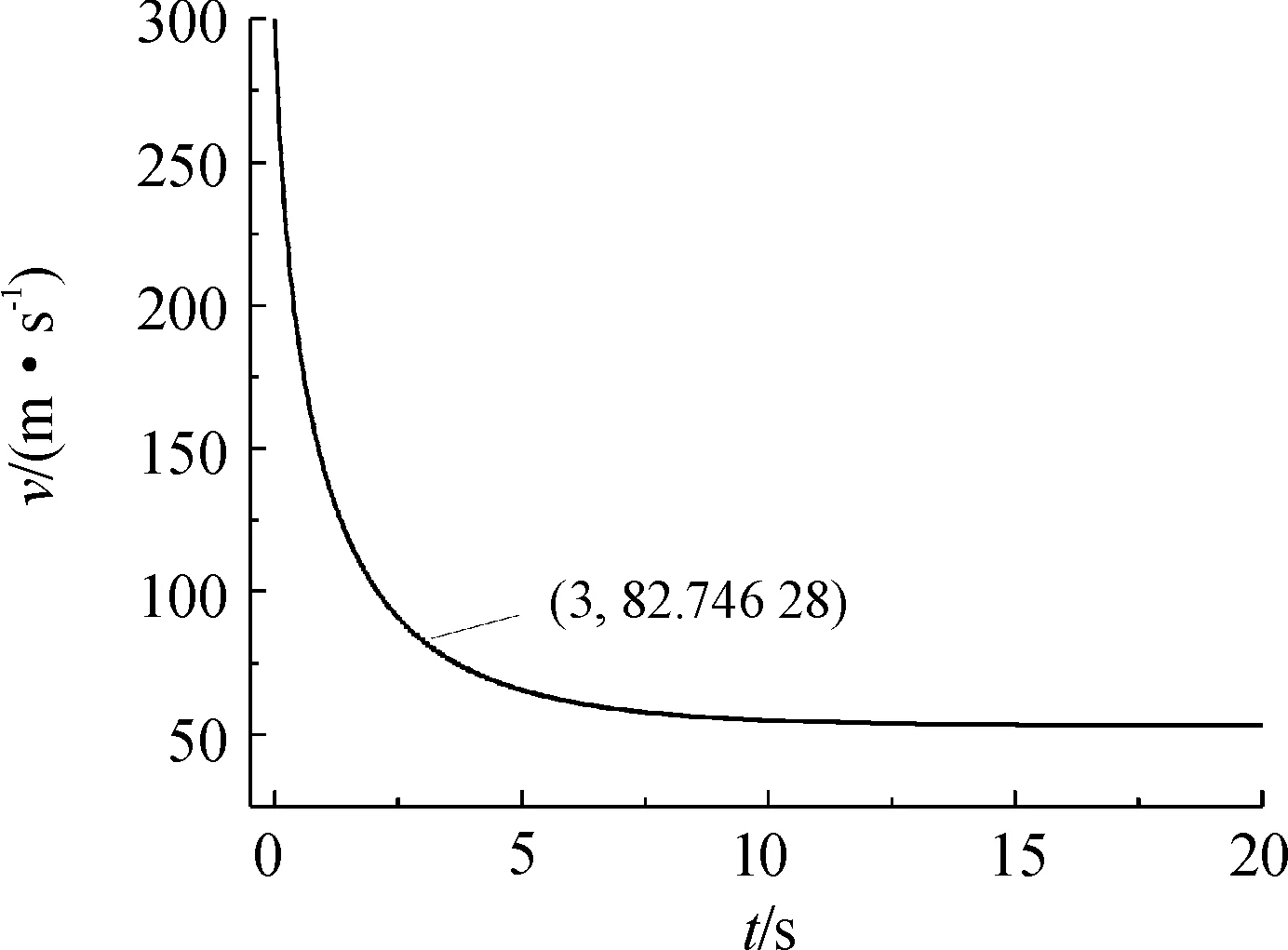
图12 子弹速度曲线

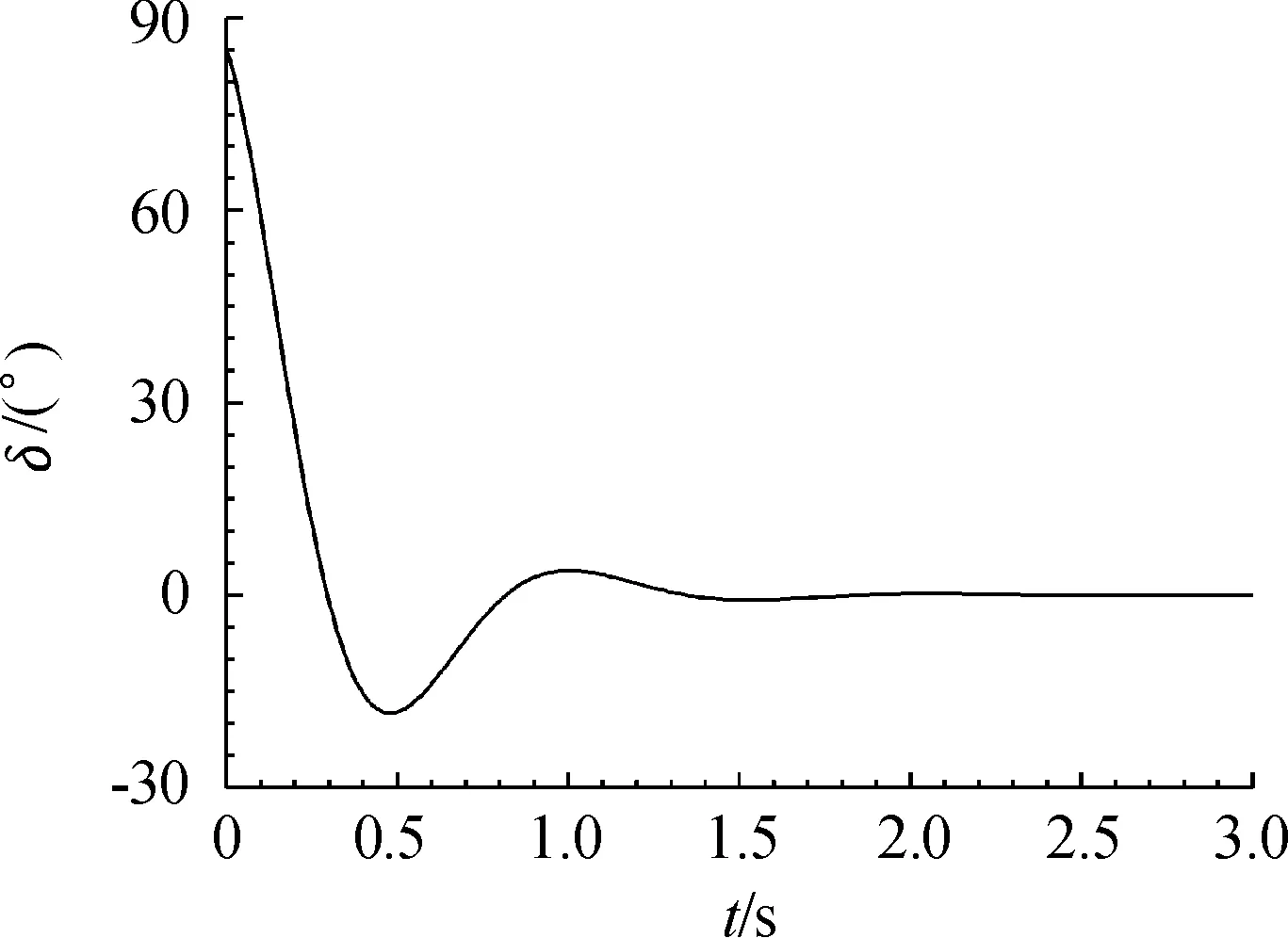
图13 子弹攻角曲线

5 结论

1)攻角为0°～10°、30°～60°时，阻力系数与其正相关，在10°～30°时，与其负相关，且在攻角大于60°时，阻力系数急剧下降；攻角在0°～10°、20°～40°、60°～90°时，升力系数与其正相关，攻角大于50°时升力系数急剧下降，且在攻角大于55°时为负值；负向俯仰力矩在攻角为0°～50°时逐渐增大，50°～90°之间变化幅度较小。

2)带充气式减速气囊的子弹在3 s内速度从300 m/s减至83 m/s，有稳定的减速效果，可为同种弹型的充气式气囊减速研究提供参考。