渗透数学思想 提升数学素养
——数形结合思想在小学数学教学中渗透的实践与思考
瞿德军
(江苏省盐城市建湖县实验小学,江苏盐城 224700)
引 言
数形结合思想就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来,通过“以形助数”或“以数解形”,抽象思维与形象思维的结合,使复杂问题简单化、抽象问题具体化,从而实现优化解题途径的目的[1]。本文按照数学课堂教学的课型分类,对如何将数形结合思想渗透到各方面的教与学中进行论述。
一、数形结合思想:概念教学
(一)概念讲解
数学概念是知识的根本,是数学学习的基础,但是,在以往的概念教学中,教师习惯用说教的方式,导致学生的参与度比较低。而数形结合思想的渗透则能够改变这一现状,教师可以通过直观图形的引入来帮助学生理解相关概念,让原本抽象的知识形象化,进而为学生直观思想的形成奠定良好的基础。
例如,在教学“加法结合律”时,为了帮助学生理解这一概念的含义,让学生理解公式(a+b)+c=a+(b+c),笔者采用“涂色”的方式(见图1)来组织学生验证“(3+2)+4=?”“3+(2+4)=?”这两组算式的计算结果。

图1
在这个“涂色”的活动中,笔者引入了小方框这一“形”,直观且形象,学生也容易理解、记忆,这比单纯地让学生记忆(a+b)+c=a+(b+c)这一公式效果要好得多。由此,学生理解了在数字和符号不变的情况下,“先算白色和灰色,再算红色”与“先算灰色和黑色,再算白色”的结果是一样的。而且,这样的数形结合也能帮助学生理解加法结合律中的推广内容,即(a+b)+c=a+(b+c)=b+(a+c),还可以推广到若干个数相加。因此,在基本概念讲解的过程中,教师可以辅以图形,将抽象概念表示形象化,进而强化学生理解,提高学生学习效率。
(二)概念应用
“学有所用”是学习的最终目的,也就是说,在概念教学的过程中,教师不仅要帮助学生理解相关的数学概念,还要让学生学会如何灵活应用。在强化学生认识、深化学生理解的过程中,教师也可以渗透数形结合思想,通过数与形的结合来帮助学生在理解概念的基础上进行应用,从而达到熟练掌握和应用的目的。
例如,在教学“分数的乘法”时,为了强化学生的认识,也为了提高学生对知识的灵活应用能力,在学生知道什么是分数的乘法后,笔者组织学生思考了两个问题(见图2)。

图2
借助图形帮助学生理解分数乘法的含义,不仅能够提高学生的应用能力,还能培养和提高学生的基本数学素养。因此,在概念应用中,教师要发挥图形的作用,强化学生的理解,确保学生在数与形的结合中对相关的概念有更加深入的理解。
二、数形结合思想:计算教学
(一)算理的理解
什么是算理?简言之,算理就是计算过程中的道理,其实,上文提到的概念应用就是对算理的应用。例如,在计算“256+63”时,根据数的组成,我们可以这样理解,256 中由2 个百、5 个十、6 个一组成,63 是由6 个十、3 个一组成。之后,百加百,十加十,一加一,该进位的进位,最后得出结果319,这其实就是算理。但是,很多学生并不理解算理,往往直接借助进位的算法来进行计算,致使出现很多计算上的错误。所以,在算理教学中,教师可以将数形结合思想引入其中,帮助学生理解算理的本质,进而提高学生对所学知识的应用能力。
(二)找规律
“找规律”也是渗透数形结合、应用数形结合思想解决问题的有效手段。在提升学生的数学推理能力的过程中,教师要教学生学会分析,使其在分析中发展思维,进而提高解答问题的能力。有例题如下。
如图3所示,图中(2)是由(1)图形中的三边中点连接而成,(3)是在(2)图形的基础上再次对形成的三角形的三边中点连接而成,请问第四个图中有几个三角形,第n个图形中又有多少个三角形?
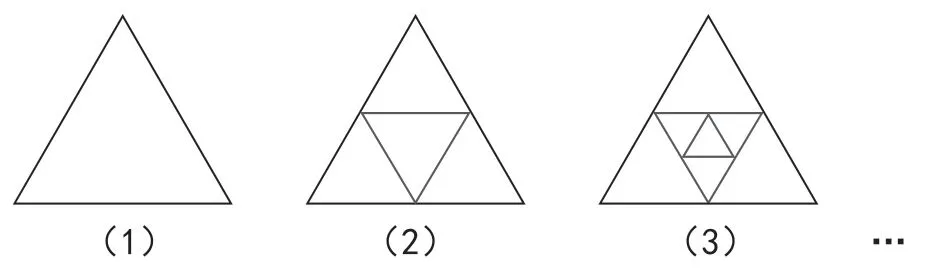
图3
对于这类找规律题,教师首先要带领学生分析图形,找到图形之间的变化规律,即第一个图是1 个三角形,第二个图是5 个三角形,第三个图是9 个三角形。之后,教师可以让学生画一画,找出第四个和第五个图中有多少个三角形,学生自然得出第四个图中的三角形有13 个,第五个图中的三角形有17 个。最后,教师可以引导学生将所得到的三角形数进行归纳,即1、5、9、13、17……这样就将原本的“数形”转化成了“数数”,学生也能很轻松地得到答案为4n-3。总之,在找规律的过程中,教师要充分发挥学生的主观能动性,鼓励学生进行独立思考,这样不但能够确保数形结合思想得到渗透,而且对学生数学思维的发展及知识灵活应用能力的提高都有促进作用。
三、数形结合思想:应用题教学
对于小学阶段的应用题,教师可以将其分成多种类型,如追及问题、相遇问题、植树问题、工程问题、列车问题等,而这些类型的问题都可以借助数形结合思想来寻找题干中的等量关系。在讲解这类应用题时,教师可以引导学生通过梳理数量之间的关系,找到解题思路,提高解题的正确率。下面以一道有关“追及问题”的试题为例进行说明。
小雷以40 米/分钟的速度,从家去商店买东西,因为忘记带钱包,5 分钟后,小羊去追小雷,结果在离家600 米的地方追到小雷,请问小羊的速度是多少?
这是一个简易图(见图4),学生可以简单画出来找关系,然后教师引导学生思考:(1)5 分钟的时候,小雷行驶了多少米?(2)小雷和小羊哪部分是等量的?(3)小羊一共行驶了多少米,用了多长时间?

图4
借助简易图,学生能够很快寻找到应用题中的等量关系,也能轻松地解答出问题。当然,这样的过程也能帮助学生形成数形结合思想,意识到其存在的价值。除此以外,在其他类型的应用题教学过程中,教师同样可以让学生采用这种画图的方式找数量关系,借助相关图形得出答案。总之,在应用题教学的过程中,教师要做好数形结合思想的渗透,让学生学会应用,进而实现辅助学生解题和提高学生推理能力的目的。
结 语
总之,数形结合思想是一种非常重要的数学思想,不仅能帮助学生理解抽象的数学知识,还能帮助学生养成良好的学习新知、解答问题的习惯,对学生数学学习效率的提高及数学学科核心素养的提升都有促进作用。在实际教学中,教师要灵活运用这一思想,在降低学生学习难度的同时,切实提升学生的学习效率。

