对两个“图解法求解平衡问题”典例的解法商榷

戎 杰 叶晟波 叶 春

(浙江省慈溪中学 浙江 宁波 315300)

求解平衡问题的方法有很多，如正交分解法、函数求解法、图解法、正弦定理法、力矩平衡法、虚功原理法等.其中，图解法是一种简单、直观、易于掌握的方法，因其抛却繁琐复杂的数学计算，为提高解题速度提供便捷，师生在解题中使用频率普遍较高.但任何一种方法绝非万能，在具体的使用过程中，一不小心也容易犯错.

文献[1]通过理论分析及典型例证的方式，对“作图法求解动态平衡问题”展开深入研究，逻辑清晰，讨论严谨.此文对“平衡问题”的教学实践产生积极的指导作用，笔者拜读后深受启示.但笔者在研读学习时，发现一处值得商榷的典例研讨，谨提粗鄙之见解.

【例1】[1]如图1所示，保持结点O的位置不动，在上面两根绳都拉直的情况下(设两绳间夹角为钝角)，下面一根绳的拉力F1保持大小不变，方向由F3的反向延长线逆时针缓慢转到F2的反向延长线的过程中，F2和F3的大小怎么变化？

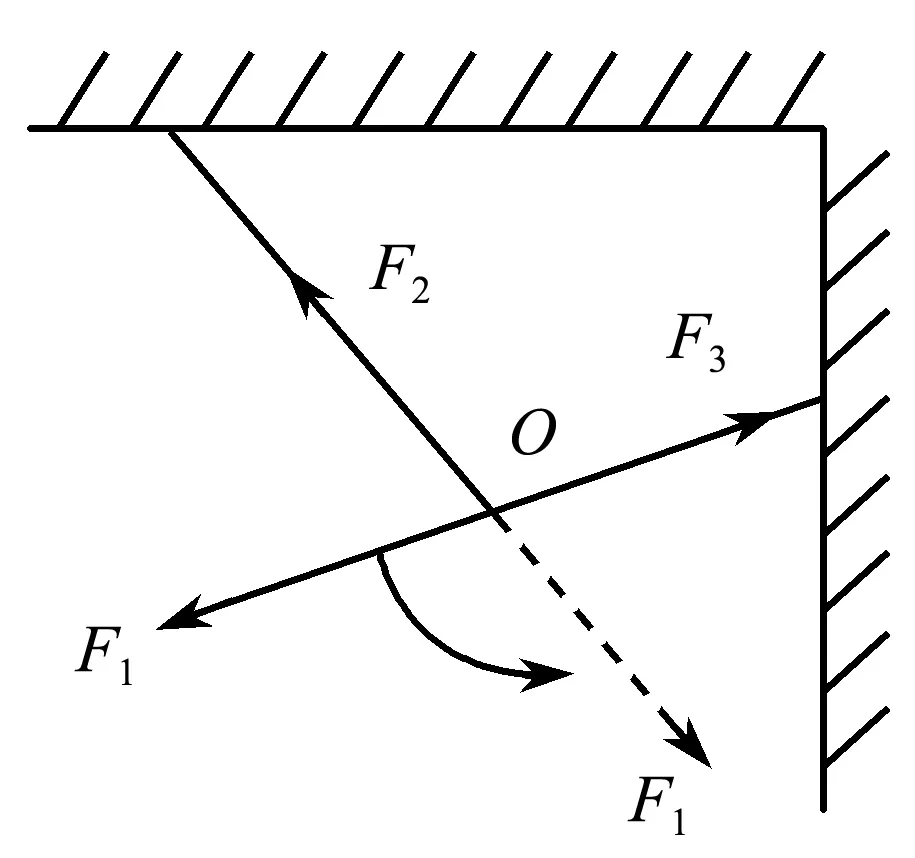
图1 例1题图

文献[1]通过作图法给出了结论：F3逐渐减小到零，F2先增大后减小到F1等大.笔者认为此答案有待商榷，分析如下.

如图2所示，以F1大小为半径r，结点O为圆心作辅助圆，圆上任意一点到O点的距离都表示拉力F1的大小.作辅助线mn平行于OR且与辅助圆相切于P点，此时OP垂直于切线mn(即F2方向).作m′n′平行于OA，与圆相切于Q点，此时OQ垂直于切线m′n′(即F3方向).

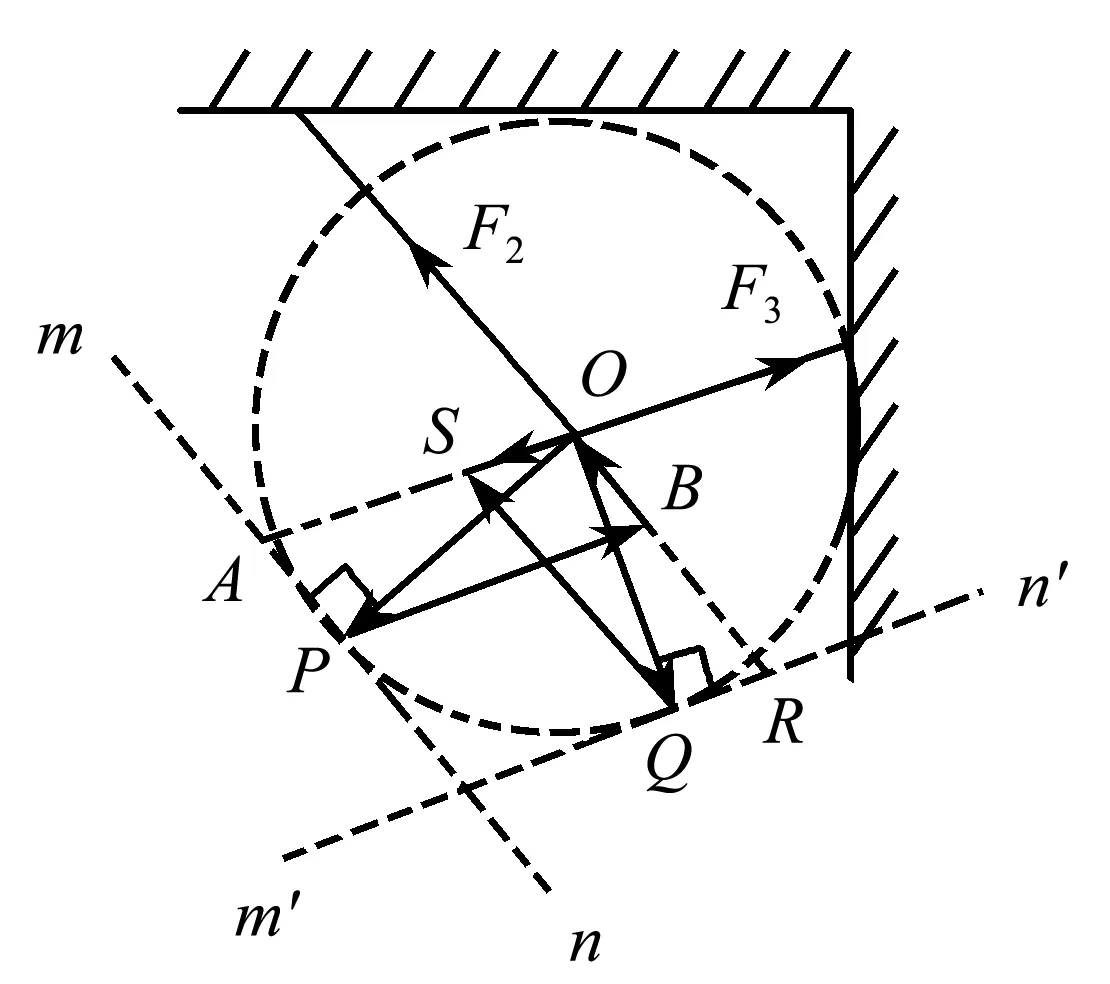
图2 笔者针对例1分析图

拉力F1从OA→OP→OR过程中，通过作图和平行四边形分析可得：

(1)F1方向从OA→OP过程中，F3增大(F3大小由圆半径r→|OA|).

(2)F1方向从OP→OR过程中，F3减小(F3大小由|OA|→0).

由此可得，F1方向转到OP处时，F3max=|OA|，即F1在转动过程中，F3先变大后变小.

同理，拉力F1方向从OA→OQ→OR过程中，有：

(1)F1方向从OA→OQ过程中，F2增大(F3大小由0→|OR|).

(2)F1方向从OQ→OR过程中，F2减小(F3大小由|OR|→圆半径r).

由此可知，F1转到OQ处时，F2max=|OR|，即F1在转动过程中，F2也是先变大后变小.

由上述分析可知，此例的正确结论应是：F3先变大后逐渐减小到零，F2由零先增大，后逐渐减小到F1.

小结：由此例来看，在使用图解法求解动态平衡问题时，要注意临界状态时各力的大小是否达到最大(最小)的临界值.因题设条件两绳间夹角为钝角，必然会有F1分别与F2和F3垂直的状态，当F1垂直于F2时，F3达到最大值；当F1垂直于F3时，F2达到最大值.故整个动态平衡过程中，F2和F3的大小变化趋势，必然是相同的(都是先变大后变小)，而这点从对称性的角度也很好理解.

针对“平衡问题”中的一类临界极值问题，文献[2]“抛却”了常规的正交分解法和函数求解法，引入“全反力”“摩擦锥”等概念，并采用图解法巧妙求解，事半功倍，展示了科学思维培养的良好路径，不失为一篇实用而富有技巧性的好文.但对于文中典例题2的求解过程，笔者有一些粗浅见解.

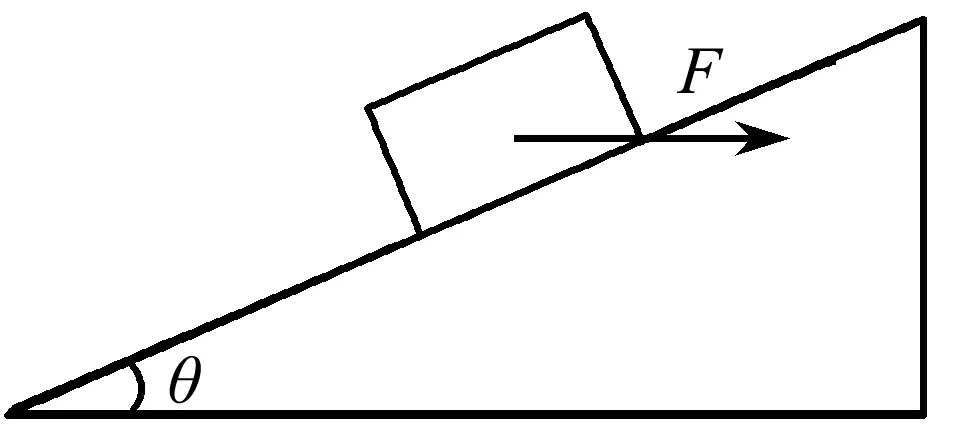
【例2】[2]如图3所示，在倾角为θ的粗糙固定斜面上，有一个质量为m的物体在水平力F作用下，恰好静止在斜面上.已知物体与斜面间的动摩擦因数为μ，且μ

图3 例2题图

文献[2]根据临界状态的特征，把“恰好静止”分为“恰好不上滑”和“恰好不下滑”两种情况，并引入“全反力”“摩擦锥”等概念，用图解法进行了分类讨论，整体思路值得借鉴学习.

(1)恰好不下滑

如图4所示，重力mg与水平推力F的合力(全反力F全)恰好在摩擦锥的边缘，此时物块恰好不下滑.

图4 文献[2]针对恰好不下滑分析图

此时全反力的反向延长线与竖直方向的夹角为α(α=θ-φ)，有

F=mgtanα=mgtan(θ-φ)

(1)

又由于μ=tanφ，可以算出

(2)

(2)恰好不上滑

对于“恰好不上滑”的临界状态，全反力F全指向左上方，全反力反向延长线与竖直方向夹角为β(β=θ+φ).因θ+φ大小未知，因此还需分两种情况讨论.

情况1：0<β<90°，如图5所示.

图5 文献[2]针对恰好不上滑0<β<90°情形分析图

F=mgtanθ=mgtan(θ+β)

(3)

(4)

文献[2]仅讨论了上述(0<β<90°)这种情况，对于β≥90°的情况，笔者认为有必要进一步讨论.

情况2：β≥90°，如图6所示.

图6 笔者针对恰好不上滑β≥90°情形分析图

在F>mgtanθ的情况下，无论F多大，重力mg与F的合力总在摩擦角φ范围内.故无论F多大，物块都能保持静止，物块处于“自锁”状态.

小结：由此例来看，β≥90°的这种情况虽不满足题干所述的“物块恰好静止在斜面上”这种临界条件.但从培养学生物理思维的严谨性，解题过程的完整性、规范性的角度来说，笔者认为第2种情况的讨论不能舍去或缺失，此举是非常重要且有意义的教学环节.此外，也是分类讨论思想在物理习题教学中的重要体现.

综上所述，文献[1,2]两文抛却繁琐的数学计算，巧用作图破解平衡，化繁为简，生动巧妙，给“平衡问题”的教学实践提供了全新思路，对两文典例求解中细节的商榷，旨在凸显对临界状态极值问题的关注，强调分类讨论的完整严密在物理教学中的重要意义，培养质疑创新能力，提升科学思维品质.