用MATLAB程序实现牛顿环的动画演示*

周群益

(广州理工学院通识教育学院 广东 广州 510540)

莫云飞

(长沙学院电子信息与电气工程学院 湖南 长沙 410022)

周丽丽

(赣南医学院信息工程学院 江西 赣州 341000)

侯兆阳

(长安大学理学院应用物理系 陕西 西安 710064)

1 引言

文献[1]在大学物理的“课程思政”与仿真实验中做了有益的探索，以牛顿环实验为例，通过MATLAB的用户交互系统(GUI)提高学生学习的积极性．不过，文献[1]中并没有说明牛顿环的数学模型，且文中的模拟结果也出现明显差错，所谓光强分布曲线应该是光波振幅的分布曲线；当中心光强为零时，干涉条纹中心应该是暗斑而不是亮斑．我们多年前就出版了MATLAB与大学物理相结合的教材，执行程序显示牛顿环变化的规律[2]．本文重新建立了牛顿环的数学模型，应用MATLAB特有的指令，用动画演示牛顿环的变化过程，以便读者掌握牛顿环动画的设计方法，解决更多的光学问题.

2 牛顿环的数学模型

如图1所示，半径很大且为R的平凸透镜与平板玻璃的距离为d，空气间隙厚度为e，e≪R，d≪R．当波长为λ的单色光a垂直入射时，在凸透镜下表面与空气的交界面同时发生反射和透射，反射光为b，透射光a′在平板玻璃的上表面再发生反射，反射光为b′．b和b′是同一束光a的两部分，因而是相干光，相遇时就发生干涉.

图1 牛顿环的光路图

由于玻璃的折射率大于空气的折射率，所以b光反射时没有半波损失，因而不会产生附加光程差；b′光反射时有半波损失，因而会产生附加光程差．空气的折射率n=1，两列光的光程差为

(1)

(2)

暗环形成的条件为

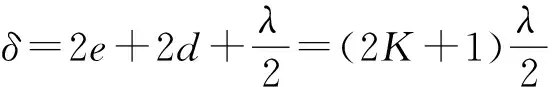
(3)

(4)

可知，相邻明环或暗环的厚度差相同.

设光环的半径为r，可得方程

r2=R2-(R-e)2

由于R≫e，所以

r2≈2Re

(5)

第k级明环的半径为

(6)

第K级暗环的半径为

(7)

当d= 0时，平凸透镜接触平板玻璃，可得

(8)

(9)

其中K=0时的暗环半径为零，表示反射光的中央是暗斑(对应的透射光是明斑)．干涉级次k或K越大，对应的厚度e也越大，明环和暗环距离中心越远．当平凸透镜向上移动时，d将增加，由于同一级干涉条纹对应同一厚度，所以条纹向中心移动，k和K较小级次条纹将逐渐消失.

当平行光垂直照射时，设入射光和反射光的振幅都为A0(A0代表光波中电场能量和磁场能量之和的振幅)，当两束光相干叠加时，合振幅为

将式(1)代入上式得

将式(5)代入上式得

(10)

光强与光波振幅的平方成正比I=kA2，其中k是比例系数．因此光强为

(11)

(12)

光强分布规律为

(13)

3 可视化

(14)

(15)

当d= 0时，相对振幅为

(16)

相对光强为

(17)

利用MATLAB的绘图指令plot可以画出光波和光强曲线，利用图像指令image可画出干涉图样，利用色图指令colormap可设定干涉条纹的颜色．结合MATLAB的程序设计方法和辅助指令，可以演示牛顿环的动画(见附录).

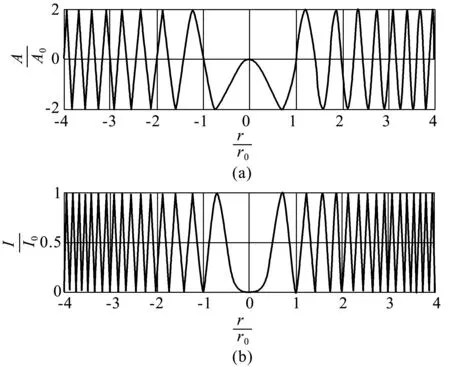
图2 牛顿环在初始时的光波振幅和光强(d=0)

如图3所示，当d=0时，牛顿环中央是暗斑，随着半径的增加，条纹间距越来越小，分布越来越密．这是因为相邻明环或暗环的厚度差相同，从里到外空气厚度逐渐增加的缘故．注意：图3显示反射光的牛顿环，对于透射光，牛顿环的明暗分布的规律正好相反.

图4 平凸镜上移时的牛顿环

4 结束语

我们认为，传统学科都要与现代计算机技术结合起来，光学与MATLAB结合，能够帮助学生更好地理解光学知识．我们10年前就花费了多年时间，撰写了MATLAB与大学物理学相结合的教材，共有300多个各类程序，其中有10多个光学程序，相信对于读者具有重要的参考价值.

附 录

NewtonRing.m

%反射光的牛顿环的动画

clear,rm=4;r=-rm:0.005:rm;%清除变量,最大半径(相对坐标),坐标向量

A=2*cos(pi*(r.^2+1/2));%反射光的相对振幅

figure,subplot(2,1,1),plot(r,A,'LineWidth',2);%建立图形窗口,选子图,画曲线

grid on,fs=16;%加网格,字体大小

xlabel('itr/r m_0','FontSize',fs)%加横标签

ylabel('itA/A m_0','FontSize',fs)%加纵标签

title('反射光的牛顿环的初始光波振幅','FontSize',fs)%加标题

subplot(2,1,2),plot(r,A.^2/4,'LineWidth',2),grid on%选子图,画曲线,加网格

xlabel('itr/r m_0','FontSize',fs)%加横标签

ylabel('itl/I m_0','FontSize',fs)%加纵标签

title('反射光的牛顿环的初始光强','FontSize',fs)%加标题

[X,Y]=meshgrid(r);R=sqrt(X.^2+Y.^2);%坐标矩阵,各点到圆心的相对距离

I=cos(pi*(R.^2+1/2)).^2;c=linspace(0,1,64)';%反射光的相对光强,颜色范围

figure,h=image(I*64);colormap([c,c*0,c*0])%建立图形窗口,画图像,形成红色色图

title('反射光的初始牛顿环','FontSize',16),axis off equal,pause%标题,隐轴,暂停

title('平凸镜上移时反射光的牛顿环','FontSize',16),d=0;%修改标题,初始距离

while 1%无限循环

d=d+0.02;I=cos(pi*(R.^2+2*d+1/2)).^2;%增加距离,反射光的相对光强

set(h,'CData',64*I),drawnow%设置光强,更新屏幕

if get(gcf,'CurrentCharacter')==char(27),break,end%按ESC键退出

end%结束循环