基于ISM法的“圆周运动”单元教学重难点分析

许君委 程小健 陶永杰

(安徽师范大学物理与电子信息学院 安徽 芜湖 241002)

1 引言

ISM(Interpretive Structure Modeling)译为解释结构模型，是由美国John Warfield教授于1973年提出的一种用于分析社会经济系统问题的典型方法[1]，它通过提取核心要素，绘制出层级有向图，将混乱无序的要素进行分级，可以更直观地展示出研究对象的构成要素及内在逻辑结构.直到1978年，日本学者佐藤博证明该方法可适用于目标分析和教材分析.目前，其在教育领域的使用途径还是以教材结构分析为主，文献[2～4]都对应用ISM法分析教材进行实例研究.但对应用ISM法分析教学重、难点的研究较少，笔者以人教版普通高中物理新教科书中“圆周运动”单元为例，应用ISM法从定量的角度分析该单元的教学重、难点.

2 ISM分析方法

运用ISM法分析“圆周运动”单元重点和难点，需要遵循ISM法的操作步骤，即：首先明确研究对象，然后提取单元的核心要素，确定要素间的形成路径，再根据形成路径制作出邻接矩阵表，关于可达矩阵有学者认为是非必须步骤，故本文未求解，通过对邻接矩阵表的分析得到层级有向表和绘制出层级有向图.

2.1 明确研究对象

在展开研究前，要明确研究的对象，笔者依据新人教版教科书，对“圆周运动”单元的标题、内容和知识点进行了提炼、罗列，其中对“转速”提炼是依据现实问题所涉及到的，周期和转速间的转换得来的，该知识点也反映这类运动的特点，如表1所示.

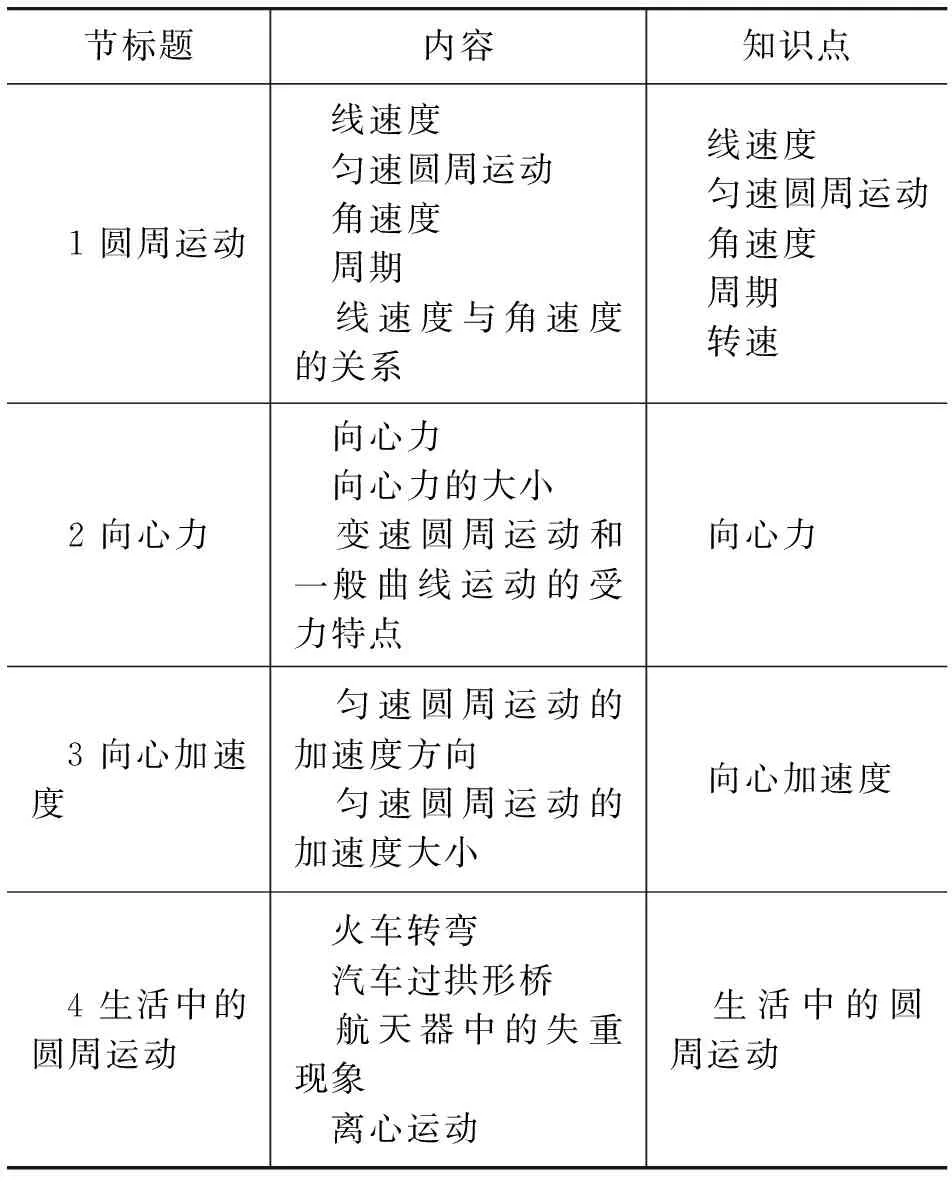
表1 第六章 圆周运动单元内容

2.2 提取核心要素

笔者在研究新人教版教科书“圆周运动”单元的基础上，结合《普通高中物理课程标准》(2017年版2020年修订)的要求：“会用线速度、角速度、周期描述匀速圆周运动.知道匀速圆周运动向心加速度的大小和方向.通过实验，探究并了解匀速圆周运动向心力大小与半径、角速度、质量的关系.能用牛顿第二定律分析匀速圆周运动的向心力.了解生产生活中的离心现象及其产生的原因.”[5]按照在教科书中出现的顺序提取出了8个核心要素，如表2所示.

表2 新人教版圆周运动

2.3 确定要素间关系的形成路径

要素间关系的形成路径是依据课程标准的内容、教科书编纂结构、学习者的认知特点以及分析者的理解决定的.在结合课程标准中对这单元内容的教学要求的基础上，给出“圆周运动”单元要素间的关系形成路径，如图1所示.

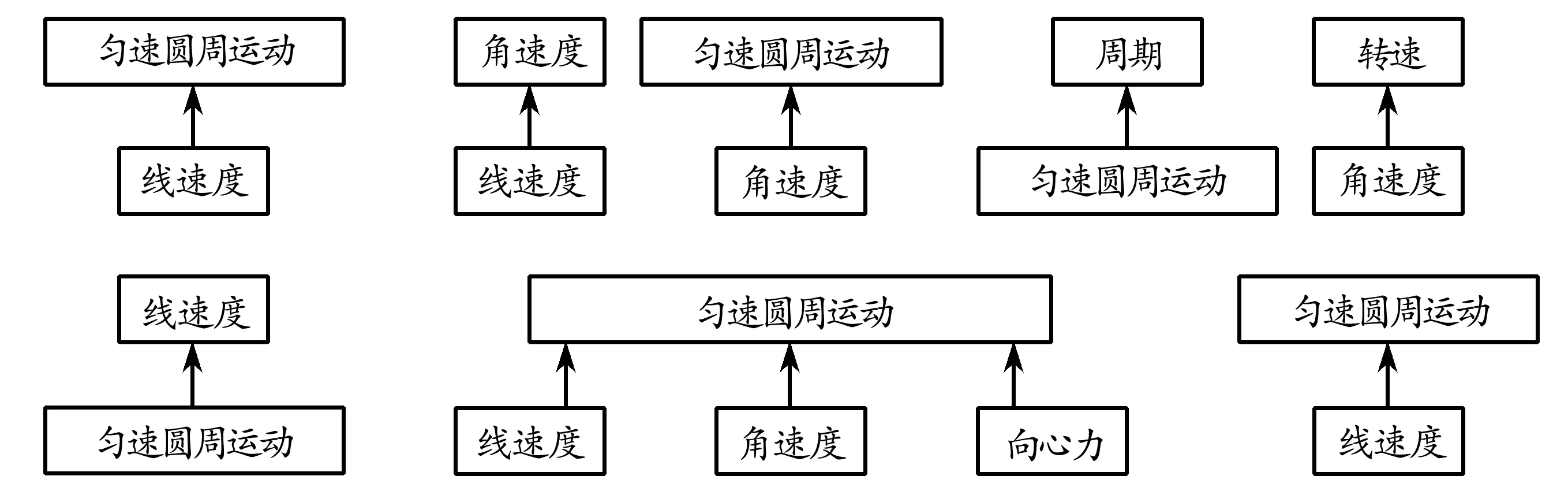
图1 各要素间关系图

2.4 邻接矩阵表

在图1中各要素间的关系得以明确，但是图中关系多且复杂，不能很好地体现知识间的有序性，故将图1转换为更加直观、有序的表格形式.依据图1中确定的要素间关系的形成路径，绘制出邻接矩阵表，如表3所示.在表中“0”表示两要素间没有形成关系，即在图1中没有形成箭头；“1”则表示要素间存在形成关系，即在图1中有形成箭头.

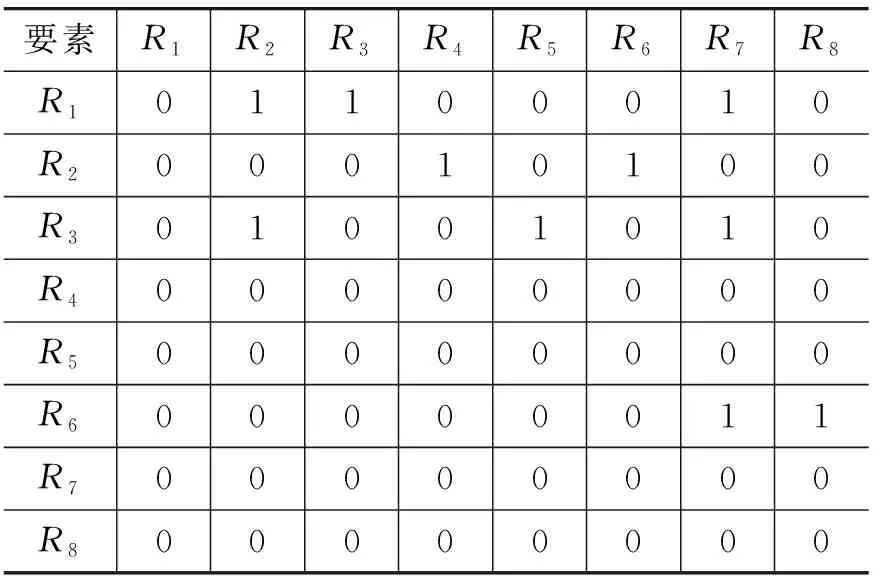
表3 邻接矩阵表

2.5 要素的层级有向表

在分析了邻接矩阵表的基础上，将要素Ri可以到达的全部要素集合Mi和所有可以到达要素Ri的集合Ni列出，并且计算出它们的交集，得出表4.

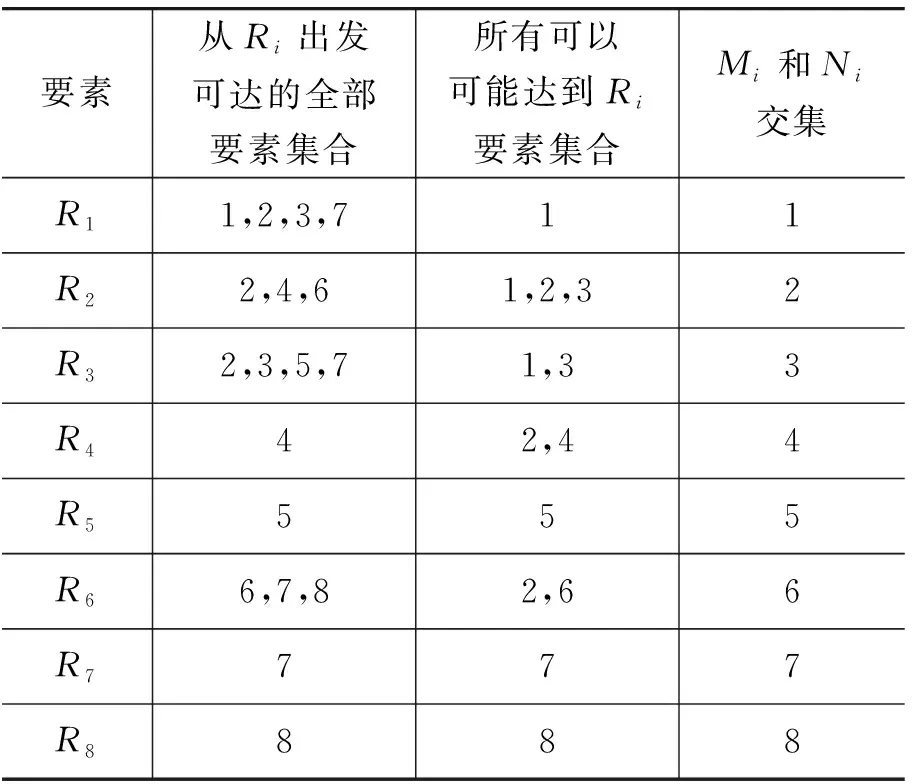
表4 可达要素与先行要素集合表

通过表4可以计算出可达集合Mi与先行集合Ni的交集，当交集内的要素Si与要素Ri一致时，就说明要素Si不可能到达除本要素之外的任何要素，规定这些要素为全部要素中的最高级要素，用相同的方法得出次高级，以此类推，可以绘制出要素的层级有向表，如表5所示.

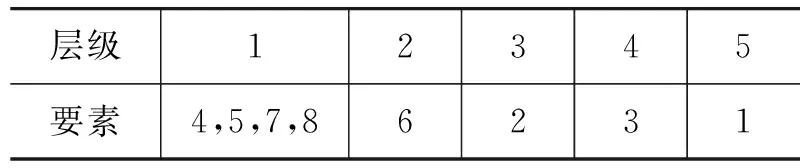
表5 层级有向表

2.6 要素间层级有向图

由于层级有向表对要素间的层级显示并不直观，故依据层级有向表绘制出了要素间层级有向图，如图2所示.

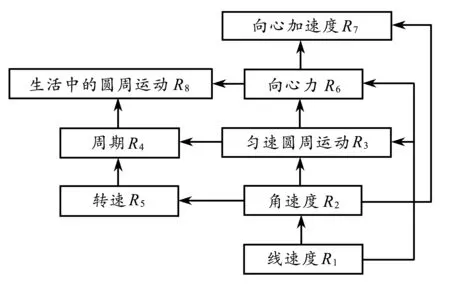
图2 层级有向图

3 “圆周运动”单元教学重点难点分析

教学的重点难点分析是教师在进行教学设计时，必须考虑的一项重要内容，只有确定好了一个单元的重点和难点，才能有针对性地进行教学设计并组织教学活动，达到更好的教学效果.文献[6]把教学重点归纳为教师把知识和技能传授给学生过程中的重要的或者主要的部分.以“圆周运动”单元为例，其教学重点是指在圆周运动单元学习过程中，能够体现该单元教学内容结构的基本特点，反映知识间逻辑关系的基础.教学难点是指以学生为标准，学生已有的生活经验、已有的基础知识和基本技能在完成某项任务或学习某个知识时遇到的困难和挫折[7].即在教材内容中，形成关系复杂，学生可能难以理解或者教材内容给出不全面，需要学生自行推演的知识要素.

通过ISM法对“圆周运动”教材结构体系的分析和对单元教学重难点概念的界定，“圆周运动”单元的教学重点和难点如下.

教学重点：依据学科课程标准和教科书内容体系，运用ISM法分析结果，在分析过层级有向图和学习者的认知特点后，可以看出“圆周运动”单元的教学重点不仅仅包括分析所得的8个核心要素，还包括如线速度和角速度间、角速度和转速间、圆周运动和周期间等一些简单的要素间形成路径，这些教学重点构建出基本的圆周运动知识的框架体系，既有助于指导教师备课、教学，又为学生提高认知水平提供帮助.

教学难点：根据学生单元学习的具体情况，运用ISM法分析结果可知，教学难点不但是这个单元教材结构中的最高层级要素，周期、转速、向心加速度和生活中的圆周运动和处在结构中心位置的向心力，还指一些需要学生自行推演的知识.例如周期和转速，它们与向心力、向心加速度的关系需要学生自己去推演，无形中加大学生学习难度.向心力和向心加速度被视为教学难点，因其处在结构中较高的位置和其形成路径复杂，对学生的知识迁移能力要求高.而生活中的圆周运动被列为教学难点，因其独特的作用，构建一些具有代表性的圆周运动模，如火车转弯模型、拱桥模型等.这些都是知识和生活实践的结合，具有培养学生科学思维的重要意义.

4 总结

通过ISM法对教材结构进行分层，把隐藏在教科书逻辑结构中的有向性总结、绘制成层级分明的要素层级有向图，可以更加直观地观察出教材内容的重点和难点.ISM这种研究方法可以呈现出单元或主题教学内容的层级关系，对理解克服难点有指向作用，同时对从定量的角度去分析和设计教学有指导性的作用.通过ISM法去指导教学更利于学生对物理知识结构的把握，进而达到培养学生高水平的物理观念和提高学生的科学思维水平的教学目的.