化学分析测量数据处理有关概念的相关商榷

岳宣峰，樊鑫，秦丹，逯昊文，张延妮

1陕西师范大学化学化工学院，陕西省生命分析化学重点实验室，西安 710062

2陕西师范大学药用资源与天然药物化学教育部重点实验室，西安 710062

1 引言

为了对测量数据进行科学的处理，现行《化学分析》教材中普遍介绍了相关化学计量学基础知识，并将其应用于对真值的预期。化学测量的基础理论是化学计量学，它通过数学及统计学方法在研究对象的“表观状态”和“真实状态”之间建立联系，并通过解析测量数据最大限度地提取被研究对象的有关特征信息。因此，教材中普遍介绍了误差、绝对误差、相对误差、系统误差、随机误差、偏差、准确度、精密度等概念，并对这些概念之间的关联也做了一定解读，这些内容涉及化学测量、统计学、数学及语言逻辑等多个学科，给教材的编写带来了很大的挑战，现行主要《化学分析》教材[1,2]在涉及以上知识的编排结构上还不甚合理，一些概念的定义还不够统一，一些概念的分类还不够清晰，还有一些知识存在可能的疏漏甚至错讹，而这些问题都是分析化学专业共同体进行理论研究和教育教学时亟待解决的问题。本文基于概念的分类规则和定义规则，对两本主要《化学分析》教材中涉及测量数据处理的概念进行了探讨，指出有关概念的命名、定义、分类、知识编排等方面存在的问题，并提出了相应的改进建议。

2 概念的分类和概念的定义

2.1 概念分类的属性及其对概念定义的内在要求

概念分类是一项复杂的工程，涉及所有学科，并且需要在一定的哲学观念的指导下进行。相对于具体学科，跨学科的概念分类就更为困难，一方面是由于综合性工程的巨大挑战，另一方面是众口难调，要取得一致的分类标准非常困难；另外，哲学思想对这项工程起着纲领性的作用，而至今真正取得不同阶层、不同民族、不同国家与文明社会认同的作为科学的哲学还没有出现。因此，那种全面统一的概念分类及其体系的实现还有一段相当长的道路要走，但这并不妨碍在同一学科内部及交叉学科之间不断对旧概念进行新分类的尝试，甚至创立新概念。构建基础概念类别应该以语言学、形式逻辑、辨证逻辑、数学、系统论等学科所涉及的广义对象为基点，有关概念分类及构建的注意事项及其与专业术语之间的关联关系见文献[3]。概念分类的外延研究要求首先明确概念的定义，定义的合理描述有助于聚焦概念最关心的关系脉络，从而提高概念运用的效率。

2.2 概念的两种定义方法

在教育研究中，当在不同的层面、从不同的角度、用不同的定义来探讨同一个概念时，往往会产生很多误解和歧义，很大一部分原因是由于对所探讨的概念没有明确客观的操作性定义造成的。所谓概念的操作性定义(operational definition)是根据可观察、可测量、可操作的特征来界定概念含义的方法，从本质上说，下操作性定义就是详细描述研究变量的操作程序和测量指标，美国的物理学家布里奇的这一观点和思想在1971年被美国的《科学》杂志列为世界五大哲学成就之一，他认为：科学上的概念如果要想避免暧昧不清，最好能以我们“所采用的测量它的操作方法”来界定。下操作性定义的方法、注意事项等见文献[4]。所有的实证性研究都必须有测量，并且所有的测量都必须把一般的抽象概念变为具体的行为指标，以便他人重复、验证和交流，因而在实际研究过程中，操作性定义和抽象性定义都是需要的，应根据研究的性质和目的灵活运用。在给概念下定义的过程中，抽象性定义可涵盖研究概念所属的基本特征，解释范围较大，具有普遍性，但往往失之笼统，无法据此测量和操纵研究的概念；操作性定义着眼概念的客观可检验性，对概念的界定清楚明确，便于操纵和测量，但往往只能涉及概念的少数特征，具有明显的排它性；当一个概念同时具有两个定义时，比较理想的方式是：先用抽象性定义描述概念的基本特征，然后再用操作性定义描述概念的操作程序和测量指标，前者为后者提供方向并指明意义。

3 《化学分析》教材中测量数据处理有关概念的相关商榷

按照以上的概念分类和概念定义规则，对现行两本主要《化学分析》教材中与测量数据处理有关的概念及相关内容展开商榷，涉及预期真值的方法、准确度的内涵及其与误差的关系、误差的抽象性定义、误差的操作性定义及分类、误差的构成、测量的正确性及其判断方法、数值的“精密度”及衡量指标、预期真值的区间表达法等，详细内容如下。

3.1 预期真值的方法

现状：教材中有准确度、误差、置信度和置信区间等概念的介绍，但没有预期真值方法的明确分类[1,2]。

商榷：以上几个概念之间的关联关系不够明晰(比如：真值→预期值→准确度→误差，这些概念引入教材时未能做好环环相扣)，各个概念适用的领域并未完全明确(比如：准确度可以用来评价平均值法预期真值的效果，但一般不用于评价区间法预期真值的效果)，涉及的内容在编排上不够紧凑(将这些概念有机统一起来的起点是：对真值的预期这个目的，然后是预期方法的分类，最后是对这些预期方法效果的评价指标，这些内容在现有教材中并未按照这一逻辑编排)，知识结构呼应性不够强(“准确度”和“误差”涉及到真值，而“置信度”和“置信区间”只涉及总体平均值，其实这些概念的展开始终都应该和测量工作的根本目的即预期真值要相呼应)。

3.2 准确度的内涵及其与误差的关系

现状：准确度是指“测量值与真值的接近程度，用误差来衡量”[1]或“分析结果与真值的相符程度，通常用误差来表示”[2]。误差越小，准确度越高；误差越大，准确度越低[1,2]。

3.3 误差的抽象性定义

现状：对于概念“误差”，教材中并未提供确切的抽象性定义[1,2]。

商榷：相对于“绝对误差”及“相对误差”这些低一级的概念，“误差”这个处于分类体系上一级的概念尚无抽象性定义，显然有待补充。

建议：误差指的是研究对象某性质的真实状况与其预期状况之间的差别。

3.4 误差的操作性定义及分类

商榷：“两种表示方法”暗含“两种方法的主体是相同的，不同仅存在于外在的表示形式”，然而“绝对误差”和“相对误差”却着眼于不同的角度，在内容和形式上都有差别，因此表述“误差有两种表示方法”有误；表述“误差可用绝对误差和相对误差来表示”既有概念分类的错误又有语意表达的错误。不同教材中绝对误差的可操作性定义本质相同，然而表达式中的符号并不统一，对应的抽象性描述也不够统一，将“分析结果”和“测量值”统一改为“预期值”更为合理；类似的问题也存在于两本不同教材[1,2]对“相对误差”的描述中，另外，描述的语言在语法及用语上也都有错误。

建议：科学上常用一个数值表示研究对象某性质的具体状态，“误差”定义中的两个状态对应的两个值分别称为真值(T)和预期值()，对于这两个值的差别，按照关注角度是绝对还是相对的差异，分为绝对误差和相对误差，前者(absolute error)用Eab表示，其表达式为后者(relative error)用Ere表示，其表达式为

3.5 误差的构成

现状：按照来源和性质的不同，误差分为系统误差和随机误差[1,2]。系统误差是由某种固定的原因造成的，具有重复性、单向性，又称可测误差。随机误差是由某些难以控制且无法避免的偶然因素造成的，大小和正负不定，无法测量、不可避免且无法校正，大量平行测量的随机误差服从正态分布，且“用-μ表示”[1,2]。

商榷：如果按照教材[1,2]中的命名及分类原则，“系统误差”和“随机误差”属于“误差”的子级概念，那么其应具有母级概念的本质特征(预期值与真值的差别)，然而“随机误差”与真值无关，“系统误差”与预期值无关，显然，这里存在子级概念外延逾越母级概念的错误。另外，“系统误差”尚无可操性定义；“随机误差”的抽象性定义和可操性定义不是联袂呈现的，不利于认知的合理建构。

按照绝对误差的定义：

3.6 测量的正确性及其判断方法

现状：无测量的正确性这一概念[1,2]。

商榷：众所周知，测量的重现性高是其准确度高的必要而不充分条件，那么是测量的哪个环节的缺失导致了这个“不充分”呢？是正确性！

3.7 数值的“精密度”及衡量指标

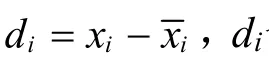
3.8 预期真值的区间表达法

商榷：测量的目的是为了预期真值，预期真值时的误差等于系统项fsys加上随机项fran，系统项是固定值，随机项出现的规律符合正态分布或者t分布，可以在计算总体平均值µ的基础上再考虑误差的系统项，就可以直接预期真值T所属的区间。另外，目前教材中给出的总体平均值µ的置信区间只是各种可能性中的一种，它是在保证优先考虑数值精密性最好的前提下的置信区间，有关这一点我们会另撰文阐述。