检出限与灵敏度关系及影响因素的探讨

漆红兰，李佳妮，张成孝

陕西师范大学化学化工学院，西安 710062

检出限(Limit of Detection，LOD)和灵敏度(Sensitivity，S)是评价分析方法的两个重要指标。国际纯粹与应用化学联合会(IUPAC)等对检出限和灵敏度推荐了明确的定义[1]。但是，有些教材和学术论文中检出限和灵敏度的使用仍然较为混乱。例如，检出限、检测限、定量限及测定限等均有使用；一些论文用检出限低表明分析方法的灵敏度高。对检出限和灵敏度及其关系和影响因素已有讨论[2–8]，但却多限于特定的方法[4–8]。因此，本文拟归纳检出限和灵敏度的定义和计算方法，探讨现代分析方法检出限和灵敏度的影响因素以及降低检出限和提高灵敏度的一些策略，抛砖引玉，共同商讨，以准确理解分析方法的检出限和灵敏度的概念和影响因素。

1 检出限和灵敏度的定义与计算

1.1 检出限和灵敏度的定义

1975年，国际纯粹与应用化学联合会(IUPAC)[1]对检出限和灵敏度推荐定义为：“The Sensitivity,Si, is defined as the slope of the analytical calibration curve. The Limit of Detection, expressed as the concentration,cL, or the quantify,qL,is derived from the smallest measure,xL, that can be detected with reasonable certainty for a given analytical procedure.”绝大多数分析化学教材均采用该定义。但是，在用词上存在细微差别。例如，武汉大学主编的《分析化学》(第五版)[9]中指出“仪器或分析方法灵敏度是区别具有微小浓度差异分析物能力的度量；检出限(detection limit)又称检出下限或最低检出量等，定义为一定置信水平下检出分析物或组分的最小量或最低浓度。”华中师范大学等主编的《分析化学》(第四版)[10]中指出“被测物质单位浓度或单位质量的变化引起响应信号值变化的程度，称之为方法的灵敏度(sensitivity)；某一方法在给定置信水平上能够检出被测物质的最小浓度或最小质量称为这种方法对该物质的检出限(detection limit)。”全国科学技术名词审定委员会(原称“全国自然科学名词审定委员会”)发行的《化学名词》(第二版)[11]推荐：“灵敏度是被测组分的量或浓度改变1个单位时分析信号的变化量。”进一步指出“在仪器分析中，分析灵敏度直接依赖于检测器的灵敏度与仪器的放大倍数。由于灵敏度未能考虑到测量噪声的影响，现在已不用灵敏度来表征分析方法的最大检出能力，而推荐用检出限来表征。”

在建立一种新分析方法或实际测定时，通常需要绘制一个分析信号y(纵坐标)随标准溶液的浓度c或质量q(横坐标)的变化曲线，称为标准曲线。在标准曲线上有一段线性部分，灵敏度即为“标准曲线线性部分的斜率”，用线性部分对应的Δy/Δc(或Δy/Δq)来表示灵敏度S。

检出限为使用统计学方法判断信号能显著区别于空白信号的最小信号值对应的最小浓度(或最小质量)。用更容易理解的一句话说，检出限就是某方法有一定的把握估计能检出某组分的最小浓度(或最小质量)。

1.2 检出限的计算

用浓度或质量分别定义LOD为：

则LOD的计算式为：

笔者将对检出限的计算参数进行进一步的讨论。

1.2.1 测量次数n

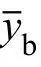
1.2.2 置信因子k

置信因子k的选择与数据服从的分布规律和置信度的确定相关。当测量数据服从正态分布时，k= 3对应的置信度为99.6%；而当测量次数有限且数据不符合正态分布时，k= 3对应的置信度大约为90%[1]。

如果测量数据服从正态分布，也可以从统计学假设检验理解检出限。如图1所示[12]，依据Currie建议[13]，先确定一个临界值(Critical value，LC)，在该值的基础上再确定检出限(Detection limit，LD)。临界值是人为设定的判断待测组分是否存在的标准，检出限是实际中能可靠检出的最小信号或最小浓度。假设低浓度范围内测量信号服从正态分布且标准偏差为常数，设定α(“实际不存在但误判为存在”的概率) =β(“实际存在但误判为不存在”的概率) = 5%，则k= 3.29[13]。

图1 假设检验法确定检出限[12]

如果测量数据服从t分布，即少量测量次数数据的分布规律，我们可以从统计学假设检验理解最小可鉴别的检测信号ymin与置信因子k、置信度P和平行测定次数n之间的关系，进而深入理解检出限。如果假设k=tP,f/n1/2，式1可转换为式6：

tP,f为统计量tP,f值表(双边)[10]查得的数值，f=n− 1。由式6可知，在空白信号和空白信号标准偏差一定的情况下，tP,f/n1/2值越大，则检出限越高。一般来说，在测定次数n相同条件下，P越高，tP,f就越大，则tP,f/n1/2值就越大。例如：t90%,2= 2.92，则tP,f/n1/2= 1.68；t95%,2= 4.30，则tP,f/n1/2= 2.48；当t99%,2= 9.92，则tP,f/n1/2= 5.73。在置信度P相同条件下，n越大，tP,f越小，则tP,f/n1/2值越小。例如：t99%,2= 9.92，则tP,f/n1/2= 5.73；当t99%,4= 4.60，则tP,f/n1/2= 2.06；当t99%,6= 3.71，则tP,f/n1/2= 1.42。在一般评价新方法时，通常选择k= 3。

1.2.3 灵敏度S

在化学测量中，测量所获信号y与浓度c的关系即标准曲线一般呈S型，如图2所示。为了便于理解，在该曲线分别标注A、B、C、D、E点，即标准曲线由AB、BC、CD、DE四段组成。LOD介于AB段；CD段为一般所称的线性范围。如果用S1、S2分别表示BC、CD段的斜率。从式4可知，k和sb一定的情况下，Sc越大，则LODc就越小。由式1可知，ymin为空白信号平均值与ksb之和。从图2左下角可以看出，ymin与S2对应的LOD2和ymin与S1对应的LOD1，因为S2>S1，则LOD2＜ LOD1。有些人用检出限低表示灵敏度高，这并不一定正确，因为检出限还与空白值的标准偏差相关。一般认为LOD为线性范围下限的1/2–1/3比较可信。

图2 标准曲线应用于剖析检出限和灵敏度关系的示意图

若测量信号与浓度的对数lgc成正比，此时检出限又该如何计算呢？电位分析法就是一个典型的例子。Dillingham等人提出了一个与IUPAC推荐相一致的检出限计算方法[14]。他们使用离子选择性电极的电位方程，E=Eϴ+β1log(a+β2) +ε，推导出计算离子选择性电极法的LOD计算式为：

式7中，β1为与温度及待测离子电荷数有关的斜率参数，β2为与干扰离子的活度、选择性、化合价有关的参数，σ是空白信号的标准偏差，a和β为假阳性率和假阴性率，zα，zβ分别为与a和β相关的标准正态分布的参数，即为与置信度相关的置信因子。

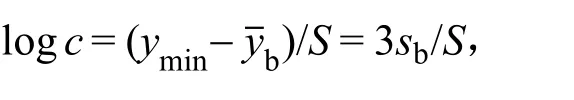
2 检出限、定量限及测定限的区别

本文拟就分析化学中几个中文名词与英文名词物理含义给予解释。全国自然科学名词审定委员会定义，测定(Determination)是借助仪器等获得某一物质的物理或化学特征数据的方法[15]。检测(Detection)是用特殊装置特定的方法对不能直接观测的目标或现象进行观察和评价的方法[16]。鉴定(Identification)是对试样中某种组分的鉴别和确定的过程[11]。测量(Measurement)是通过实验获得并可合理赋予某量一个或多个量值的过程[17]。笔者认为，测定(Determination)侧重表达定量分析的概念；定量(Quantification)也侧重表达定量分析的概念；检测(Detection)侧重表达定性分析的概念；鉴定(Identification)侧重表达识别的概念；测量(Measurement)是按照某种规律，用数据来描述观察到的现象，即对事物做出量化描述。

定量限(Limit of Quantification，LOQ)与检出限(LOD)为两个不同的参数。全国自然科学名词审定委员会发行的《化学名词》(第二版)推荐[11]，定量限为“根据统计学原理给出的用于估算能定量测定分析物的最小含量或浓度。若样品中存在的分析物的量大于该量值，则可认为该样品可以某一相对标准偏差被定量测定。在误差分布遵从正态分布的条件下，以适当的置信概率(95%)被定量测定的最小含量或浓度。”Currie建议[13]，“Quantification limits are defined in terms of a specified value for the relative standard deviation”。美国化学会环境改善委员会(ACS Committee On Environmental Improvement)建议[18]，LOD =Sb+ 3σ，LOQ =Sb+ 10σ，其中Sb是空白信号测量的平均值，σ是空白信号测量的标准偏差。图3将浓度划分为三个区域，理解LOD和LOQ的区别。若实际浓度小于LOD，则认为“未检出”；若实际浓度在LOD–LOQ之间，则认为可“定性检测”；若实际浓度大于LOQ，则认为可“定量测定”。

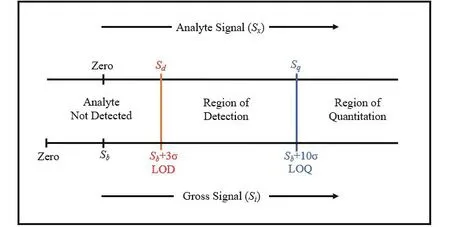
图3 检出限、定量限将浓度分为三个区域[18]

测定限(Limit of Determination，Determination Limit)为定量分析实际可能测定的某组分的下限[11]。因此，检出限与定量限和测定限为三个不同的参数。

3 影响灵敏度的因素和提高灵敏度的策略

如前所述，灵敏度为单位浓度(或质量)变化而引起的测量信号的变化(Sc= Δy/Δc，Sq= Δy/Δq)。对于信号增强法，其值为正；对于抑制法，其值为负。测定方法的灵敏度主要取决于测定体系物质的性质(包括溶液条件)、测定仪器参数和所用仪器设备等因素。

对于给定的化学和生物分析方法，测定物质转化为测量信号是关键因素。分析方法可分为直接法和间接法。直接法是直接利用待测物质产生的测量信号进行测量的方法；间接法是将待测物质转化为可产生测量信号的物质进行测量的方法。以下影响因素和策略是针对产生测量信号的物质进行讨论的。

1) 光度定量分析法

2) 荧光定量分析法

其定量公式为：If=2.3kφfI0εbc。2.3kφfI0εb即方法的灵敏度S。选择荧光量子产率φf大和ε大的物质是提高S的关键；选择入射光强度I0大和仪器参数k大的仪器和b大的测量池，也可提高S。使用激光光源可提高I0，也允许使用较大的b。好的荧光分光光度计有较好仪器放大因子k，也常受到青睐。

3) 伏安分析法

对于平面电极，线性扫描扩散电流定量公式为Randles-Sevcik方程：ip= 2.69 × 105n3/2Do1/2Av1/2c。其中ip为峰电流(A)，n为转移电子数，Do为扩散系数(cm2∙s−1)，A为电极面积(cm2)，v为扫描速率(V∙s−1)，c为待测组分浓度(mol∙cm−3，或mol∙mL−1)。2.69 × 105n3/2Do1/2Av1/2即方法的灵敏度S。由此可见，增大电极面积A，增大扫描速率v，增大扩散系数D等，则可增加峰电流。但是，应注意测得的峰电流为残余电流和扩散电流之和。残余电流主要包括杂质电流和充电电流ic。充电电流ic= ACdv，式中Cd为电极的微分电容。由此可见，增大扫描速度，充电电流的增加比扩散电流的增加更快，不利于检出限的降低；但形式上增加了方法的灵敏度。

对于分析化学研究者，对于给定的体系，常常研究化学或生物信号放大策略以提高方法的灵敏度。例如，酶催化放大策略是利用检测物的循环利用进行物质放大的策略；有些纳米信号放大策略是利用纳米材料对信号物质的多负载提高测量信号的策略；生物信号放大策略如PCR是进行检测基因片段物质放大的策略。又如，对于伏安法测定方法尽量设计成基于测量平行催化电流的方法，ica=nFAD1/2(kfcz)1/2c，式中kf为均相反应速率常数，cz为氧化剂(或还原剂)浓度，c为待测物(催化剂)浓度。相对于扩散电流体系或kf小的催化体系，选择kf大的体系就可以提高灵敏度。

4 影响检出限的因素和降低检出限的策略

背景噪声主要来源于仪器背景、化学背景和生物背景噪声[19,20]。仪器背景噪声主要来源于电子元件的噪声，如光电倍增管的暗电流，可选择暗电流小的光电倍增管；如温度变化引起电子元件信号的波动，可选择恒温体系减小此种波动；又如伏安分析中外电场或磁场引起的电流波动，可选择法拉第笼减小外电场的干扰。化学背景即为杂质或未知物质产生的微小信号。可通过提纯试剂和溶剂来减小这类背景，也可以加入大量某种物质使化学背景恒定而进行扣除。在实际工作中，样品中常常存在干扰物质，干扰物质产生的负干扰或正干扰并不属于此类。生物背景主要来源于检测生物体系(组织、细胞等)中未知物质产生的微小信号。对于这类背景应选择标准的组织或细胞等，一般使产生的生物背景尽量恒定，再进行扣除。

上述重点讨论了与标准曲线相关的灵敏度和检出限。在实际工作中，常常需要绘制工作曲线进行定量分析。即根据实际样品，并考虑消除各种干扰而加入合适的试剂或适当地改变仪器测量参数绘制工作曲线。近年来，关于生物分析和生物传感器中灵敏度和检出限的讨论备受关注[19–21]。在生物分析中，生物背景对分析结果影响最大。当生物传感器检测实际生物样品时，样品基体中的生物大分子会干扰待测组分与传感器之间的相互作用，导致传感器的性能变差。例如，毛兰群[19]指出，植入式传感器在活体检测一定时间后，由于周围生物层的形成以及体内的免疫反应，会影响其分析性能，甚至出现信号异常和传感器故障。在实际样品中计算获得待测物质的检出限可能高于标准溶液求得的检出限。复杂生物样品中的分析结果有时也会优于标准溶液中的分析结果，例如，血样中抗原与抗体的结合能力大于缓冲溶液中两者的结合能力，在血样中分析有利于免疫分析方法分析性能的提高[20]。因此，对于新建立的某一新分析方法的性能评价，应报告该方法在标准溶液中以及在真实的样品中的灵敏度和检出限。因为后者更切合实际分析。

本文剖析了灵敏度和检出限的经典定义及计算公式，讨论了影响方法灵敏度和检出限的因素，对提高灵敏度、降低检出限提出了一些策略。总体而言，分析方法的灵敏度和检出限，两者相辅相成，不能孤立使用。本文旨在抛砖引玉，引起大家对方法灵敏度和检出限的概念及影响因素的关注与思考，共同商讨，以促进两者的规范使用。