掘进巷道热环境影响因素重要性分析

董孝通， 边梦龙， 王二雨

(内蒙古科技大学 矿业与煤炭学院， 内蒙古 包头 014010)

0 引言

随着开采深度加深，矿井深部热害问题日益严峻，其中掘进巷道因特殊的形态结构，热量难以散失，热害问题更加严重[1-4]。采掘设备放热、矿石氧化放热、围岩放热与人体放热等是掘进巷道的热源[5]，工作人员长期处于掘进巷道热环境下会引发各种身体疾病甚至危及生命安全。为减少掘进巷道热环境对工作人员的影响，需要对掘进巷道热环境的影响因素进行研究。文献[6-8]得到风流参数对热环境的影响效果及通风前后巷道风流场与温度场的分布规律。文献[9-10]发现采取措施降低围岩温度，对巷道热环境影响显著。文献[11-12]得出长距离送风和短距离抽风是最有效率的通风方式，不同送风参数对巷道热环境的影响效果不同。文献[13-15]发现采取分段降温、辅助通风或新型降温技术等措施对巷道热环境有着不同程度的影响。但目前大多数研究仅讨论了单一因素对巷道热环境的影响，未涉及多因素对掘进巷道热环境影响的重要性。鉴于此，本文利用Fluent软件对不同入风风速、入风温度、围岩温度和风筒直径条件下的掘进巷道温度进行数值模拟，并对数值模拟结果进行多元线性回归拟合，可为改善掘进巷道热环境提供参考。

1 数值计算模型与因素选取

1.1 数值计算模型

掘进工作面风流流动条件较为复杂，影响因素较多，为了数值模拟求解的简便，将实际问题进行简化并做出以下假设：① 风流不可压缩，忽略流体黏性力做功，忽略水蒸气蒸发与瓦斯因素。② 将气体物理特性参数看作常数，流动为稳态紊流并满足Boussinesq假设。③ 围岩均质且各向同性，围岩温度与风流温度充分进行热交换。④ 巷道初始温度等于原岩温度。⑤ 气流在巷道内的流动满足质量守恒、能量守恒及动量守恒定律。

质量守恒方程为

(1)

式中：ρ为空气密度，kg/m3；t为时间，s；xi为坐标系中i方向上的空间位置，m；ui为坐标系中i方向上的气流速度，m/s；Sm为其他自定义源项。

能量守恒方程为

(2)

式中：θ为温度，℃；u为速度，m/s；k为流体的传热系数；cp为比热容，J/(kg·℃)；St为其他热源，℃。

动量守恒方程为

(3)

式中：uj为坐标系中j方向上的气流速度，m/s；p为修正时均压力，Pa；τij为应力张量，Pa；xj为坐标系中j方向上的空间位置，m；gi，Fi分别为坐标系中i方向上的重力和外部体积力，N。

1.2 因素选取

风流在掘进巷道中会与围岩发生热交换，在不考虑其他因素的情况下，巷道风流流动热交换方程为[16]

Q=KA(θb-θa)

(4)

式中：Q为总换热量，W；K为热交换系数，W/(m2·℃)；A为风流与围岩的换热面积，m2；θb为围岩温度，℃；θa为入风温度，℃。

由式(4)可知，围岩温度、入风温度的改变会使总换热量发生改变。根据对流换热理论，热交换系数会随着入风风速的改变而改变，且改变风筒直径会影响风量，进而影响巷道热环境。因此，本文选取入风风速、入风温度、围岩温度和风筒直径4个因素，分析其对掘进巷道热环境影响的重要性。

2 三维模型

依据招金矿业股份有限公司夏甸金矿-700 m水平掘进巷道进行1∶1三维建模，如图1所示。巷道断面为三心拱，长92 m，宽3.5 m，直墙高2.45 m，拱高0.75 m，左侧压入式通风，风筒圆心距地面2.45 m，风筒出口距掘进工作面10 m。在距离掘进工作面10，20，30，40，50，60，70，80 m处布置8个监测断面A—H，如图2所示。

图1 掘进巷道三维模型Fig.1 Three-dimensional model of tunneling roadway

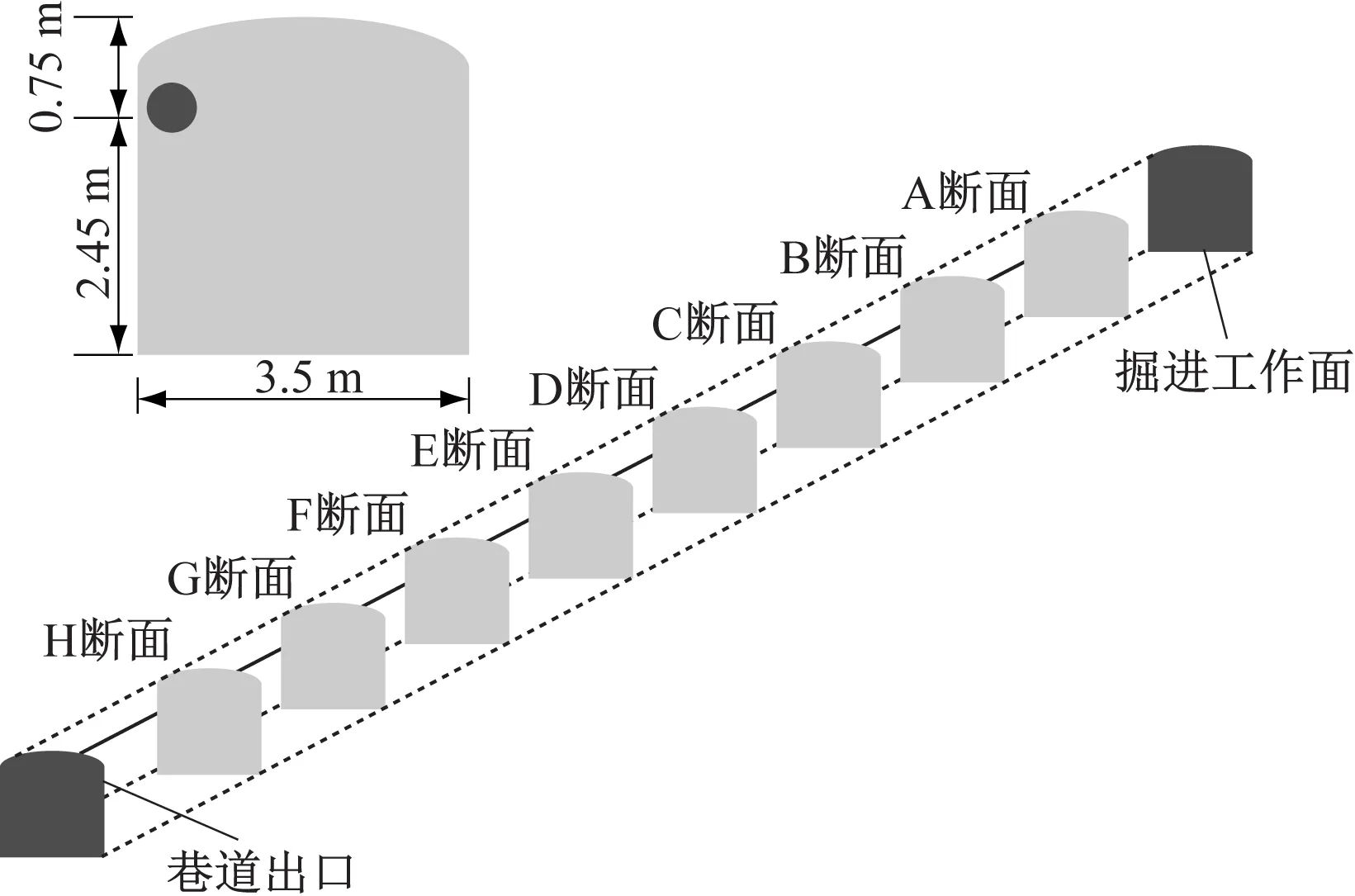
图2 巷道监测断面分布Fig.2 Roadway monitoring section distribution

对巷道三维模型进行网格划分，然后将模型导入Fluent进行边界条件与求解设置。将风筒出口设置为入口边界并定义为速度入口，巷道出口设置为出口边界并定义为自由出流边界，求解器选用稳态求解器，求解模型为标准k-ε湍流模型，待计算收敛后，读取各断面温度。

3 模拟结果及分析

3.1 正交试验

将入风风速、入风温度、围岩温度和风筒直径4个因素作为正交试验研究对象，每个因素选取3个水平，因素取值见表1。

以A，D，G 3个断面的平均温度为试验指标，根据表1进行9次正交试验，试验方案及结果见表2。由表2可知，满足3个断面都小于28 ℃的只有方案1、方案6与方案8，这3个方案的共同点是围岩温度较低。

极差是判断因素重要性程度的重要指标，极差越大，表明因素对于试验指标的重要性程度越高。根据正交试验结果进行极差分析，结果见表3。由表3可知，围岩温度的极差最大，其次为风筒直径、入风温度，入风风速的极差最小，表明对掘进巷道热环境的影响程度由大到小依次为围岩温度、风筒直径、入风温度、入风风速；入风风速、入风温度和风筒直径在不同断面下的极差相差较小，表明这3个因素对掘进巷道热环境的影响程度保持稳定；围岩温度在不同断面下的极差相差较大，距离掘进工作面越远，围岩温度对掘进巷道热环境的影响越显著。

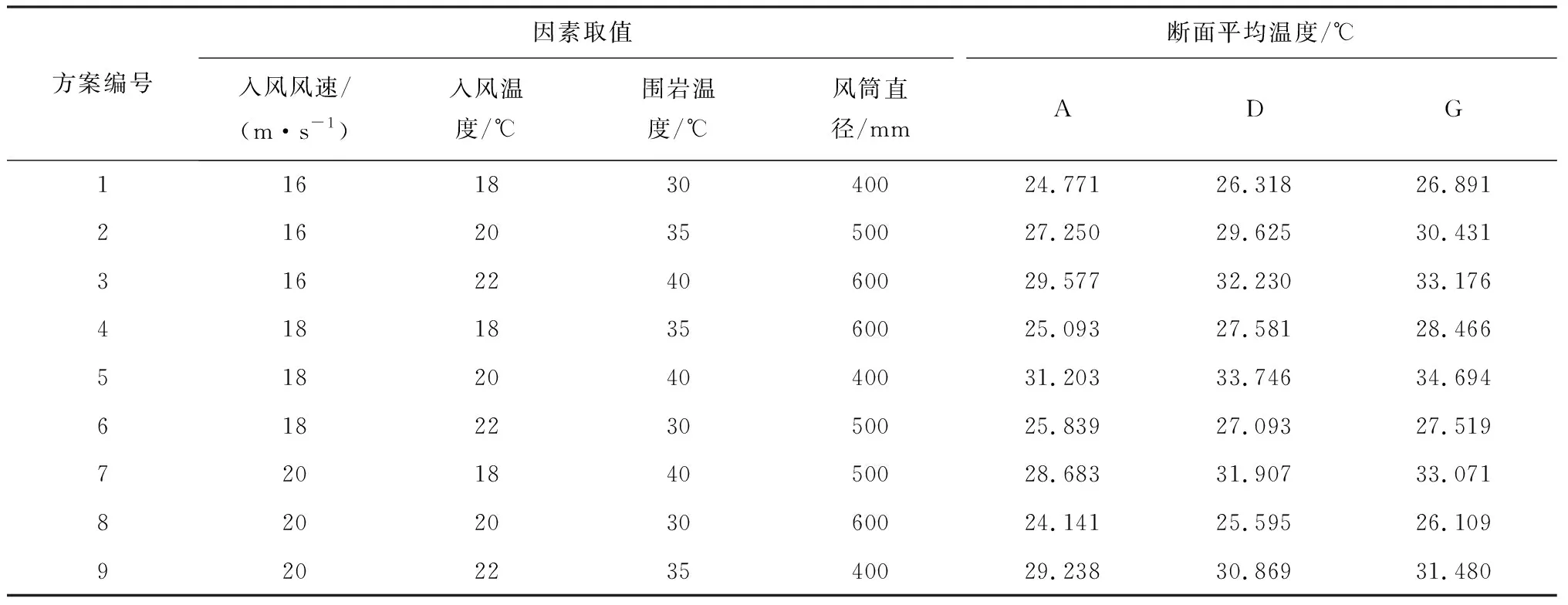
表2 正交试验方案及结果Table 2 Orthogonal test scheme and results

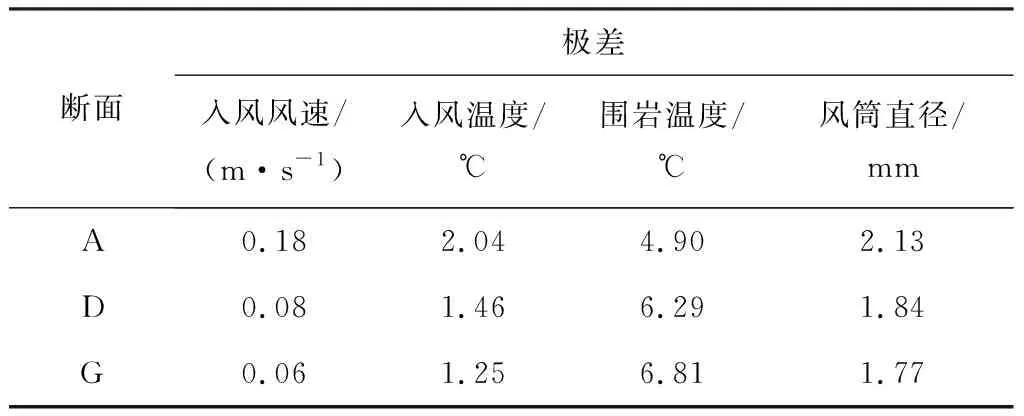
表3 极差分析结果Table 3 Range analysis results

3.2 控制变量法

3.2.1 入风风速对巷道温度的影响

设置入风温度为18 ℃，围岩温度为34 ℃，风筒直径为500 mm，入风风速分别为8，12，16，20，24 m/s，根据数值模拟结果进行拟合，拟合曲线如图3所示，拟合公式为

(5)

式中s为入风风速，m/s。

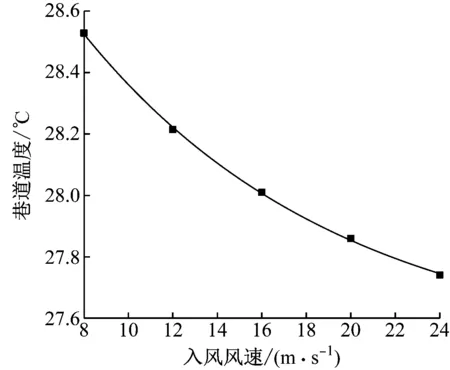
图3 不同入风风速下巷道温度Fig.3 Roadway temperature under different inlet wind speeds

由图3可知，巷道温度随着入风风速增大而降低，两者呈负幂函数关系；当入风风速从8 m/s增大至12 m/s时，巷道温度从28.528 ℃降至28.215 ℃，降低了0.313 ℃，当入风风速从20 m/s增大至24 m/s时，巷道温度从27.860 ℃降至27.741 ℃，仅降低了0.119 ℃，表明随着入风风速增大，巷道温度下降速率逐渐变小，降温效果越来越不明显。

3.2.2 入风温度对巷道温度的影响

设置入风风速为16 m/s，围岩温度为34 ℃，风筒直径为500 mm，入风温度分别为16，18，20，22，24 ℃，根据数值模拟结果进行拟合，拟合曲线如图4所示，拟合公式为

θ=21.270 75+0.374 4θa

(6)

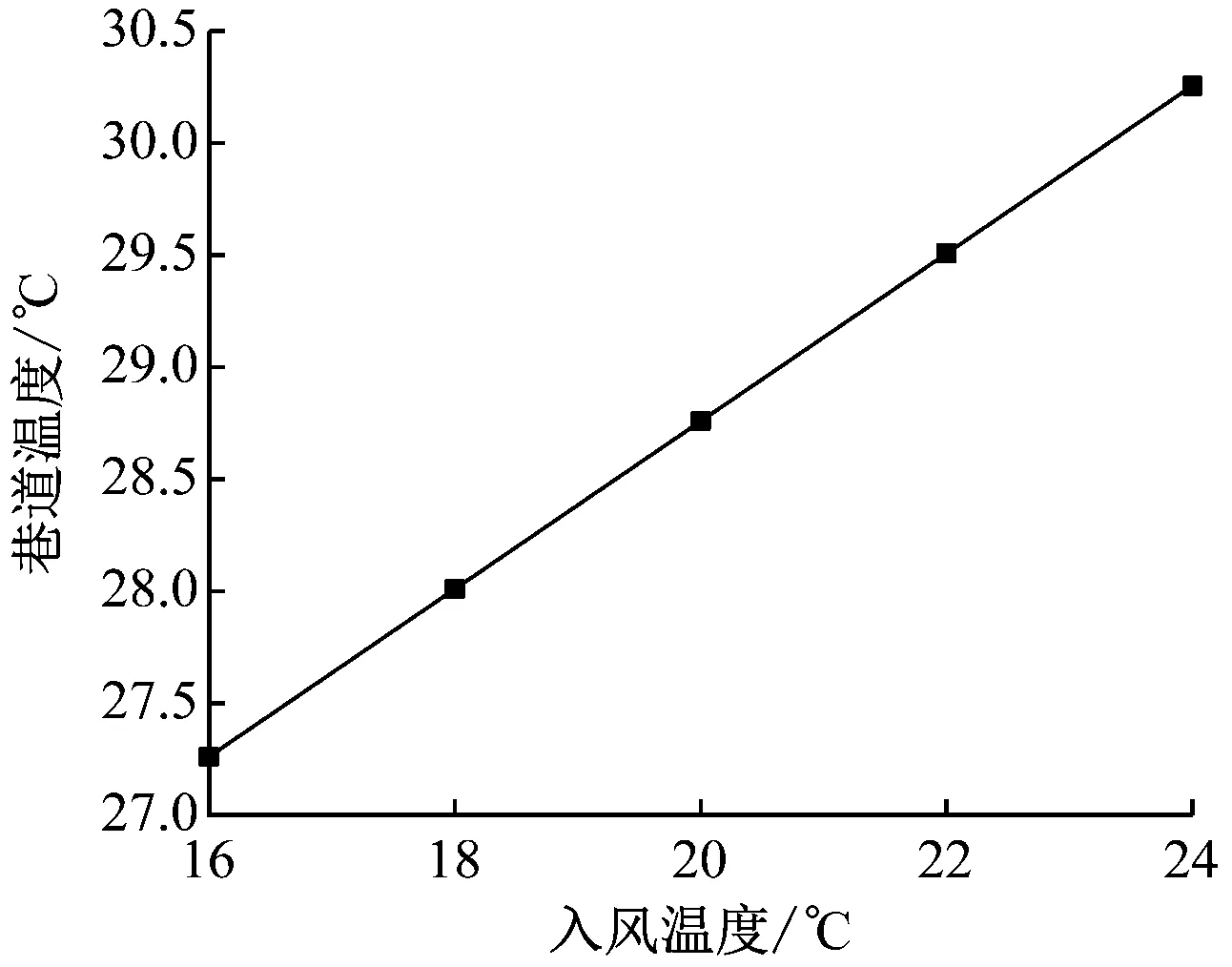
图4 不同入风温度下巷道温度Fig.4 Roadway temperature under different inlet air temperatures

由图4可知，巷道温度随着入风温度升高而升高，两者呈线性正相关关系。

3.2.3 围岩温度对巷道温度的影响

设置入风风速为16 m/s，入风温度为18 ℃，风筒直径为500 mm，围岩温度分别为32，34，36，38，40 ℃，根据数值模拟结果进行拟合，拟合曲线如图5所示，拟合公式为

θ=6.738 81+0.625 63θb

(7)

图5 不同围岩温度下巷道温度Fig.5 Roadway temperature under different surrounding rock temperatures

由图5可知，巷道温度随着围岩温度升高而升高，两者呈线性正相关关系；图5曲线斜率(0.625 63)明显大于图4曲线斜率(0.374 4)，表明围岩温度对巷道温度的影响程度更大，与正交试验结果一致。

3.2.4 风筒直径对巷道温度的影响

设置入风风速为16 m/s，入风温度为18 ℃，围岩温度为34 ℃，风筒直径分别为400，450，500，550，600 mm，根据数值模拟结果进行拟合，拟合曲线如图6所示，拟合公式为

θ=33.040 17-0.010 33d

(8)

式中d为风筒直径，mm。

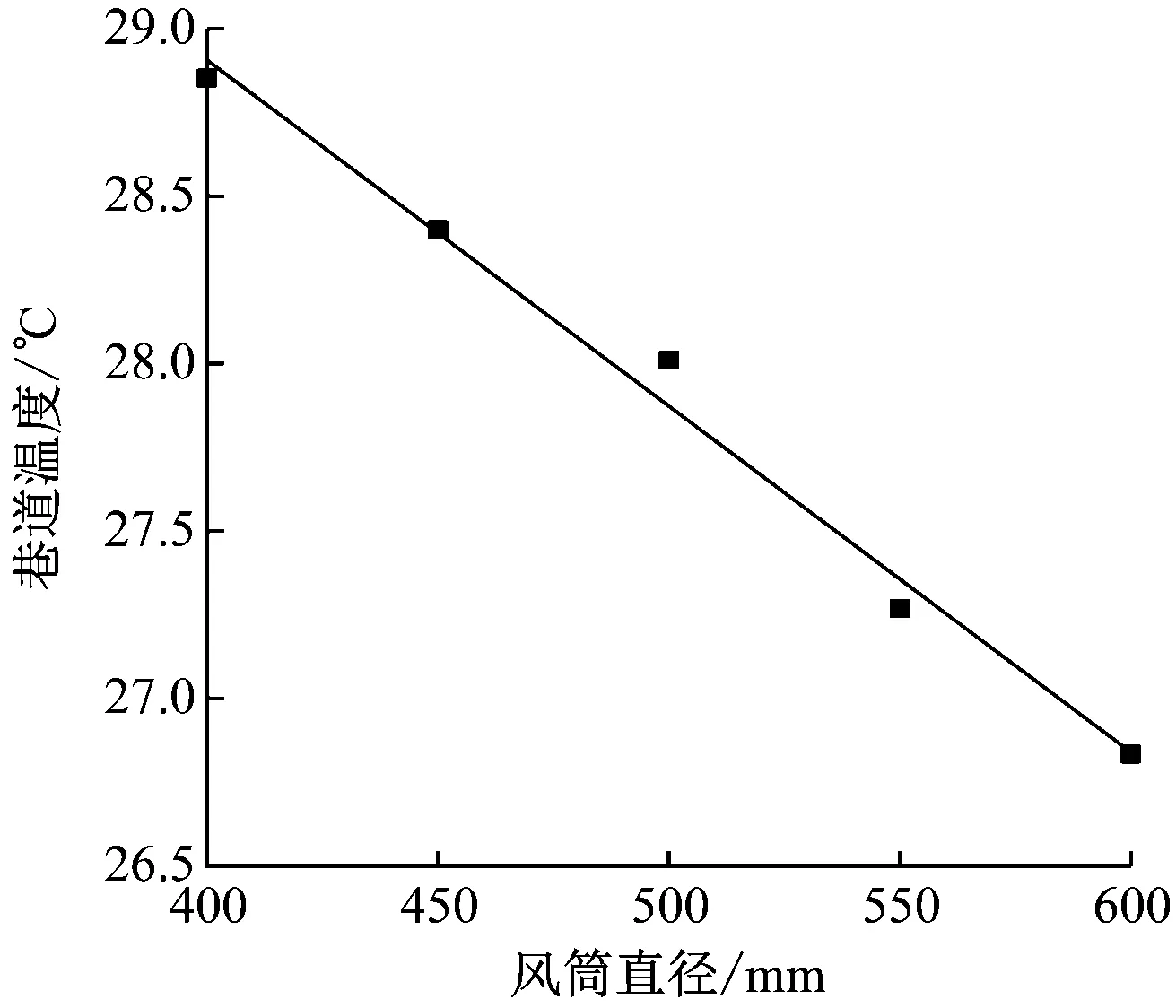
图6 不同风筒直径下巷道温度Fig.6 Roadway temperature under different air ducts diameters

由图6可知，巷道温度随着风筒直径增大而降低，两者呈线性负相关关系。原因是当能耗相同时，风筒直径增大，其风量比将以风筒直径比的1.667次方增加[17]，风量的增加对通风降温十分有利。

3.3 多元线性回归

依据正交试验和控制变量分析的数值模拟结果，以掘进巷道温度为目标因子，利用Origin进行多元线性回归分析，得到多元线性回归方程：

(9)

式(9)拟合优度为0.993 1，拟合程度较好，表明掘进巷道温度与各因素之间的线性关系较为显著。

将通过多元线性回归方程计算得到的掘进巷道温度与数值模拟得到的掘进巷道温度进行对比，结果如图7所示。可看出除个别试验的方程计算结果与数值模拟结果略有偏差外，整体趋势一致且误差较小，表明该多元线性回归方程可为工程预测掘进巷道温度提供参考。

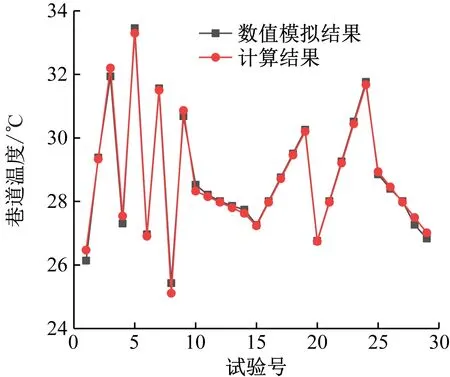
图7 方程计算结果与数值模拟结果对比Fig.7 Comparison of equation calculation results and numerical simulation results

4 结论

(1) 掘进巷道热环境影响因素重要性从大到小依次为围岩温度、风筒直径、入风温度、入风风速。入风风速、入风温度和风筒直径对掘进巷道热环境的影响程度保持稳定；距离掘进工作面越远，围岩温度对掘进巷道热环境的影响越显著。

(2) 掘进巷道温度与入风风速之间呈负幂函数关系，通过增大入风风速可降低掘进巷道温度，但随着入风风速增大，温度下降速率逐渐变小，降温效果越来越不明显；掘进巷道温度与入风温度和围岩温度之间呈线性正相关关系，与风筒直径之间呈线性负相关关系。

(3) 利用Origin进行多元线性回归分析，得到掘进巷道温度与入风风速、入风温度、围岩温度、风筒直径之间的多元线性回归方程，可为工程预测掘进巷道温度提供有效参考。