煤矿井下连续采煤机定位方法研究
贺建伟
(1.中国煤炭科工集团太原研究院有限公司, 山西 太原 030006;2.山西天地煤机装备有限公司, 山西 太原 030006)
0 引言
连续采煤机适用于“三下”压煤、不规则块段及残采区的采煤作业,也可用于巷道掘进。连续采煤机在掘进或采煤过程中大多使用传统的点激光光源对其方向进行指示,采掘司机通过目视断面上的激光光斑控制截割[1]。该方法由于掘进工作面粉尘较大、作业现场光线差、操作人员视线受装备机身遮挡等,难以准确判断截割部位置。同时随着掘进装备的掘进深入,点激光光源需要多次移站跟进,指示精度降低,且测量工作量大,无法满足工作面无人化远程操控的要求,因此,如何实现连续采煤机井下精准定位定向成为目前亟需解决的关键问题。
煤矿井下由于环境特殊且条件恶劣,GPS等地面应用较多的导航定位系统无法在井下完全发挥作用[2]。惯性导航系统作为一种自主式定位定向系统,适用范围广,不依赖外界信息便可获得载体的姿态、速度及位置信息,对煤矿井下采掘装备进行定位定向指示具有较好的效果。
当前较为主流的井下采掘装备定位方法大多依附于惯导系统进行[2],但惯导系统需通过对测量得到的加速度信息进行二次积分才可获得载体的位置信息,存在随时间累积会产生较大位置漂移误差的缺陷[3]。目前多使用基于惯导的多传感器组合定位方法解决单独使用惯导系统进行定位存在的位置漂移误差问题。文献[4]将惯导和里程计相结合进行井下采掘装备的定位研究,利用卡尔曼滤波结合里程计测得的里程信息对惯导相应测量数据进行校正,但采掘设备在井下易受浮煤影响造成履带打滑及滑移现象,此时里程计的测量误差会远大于惯导自身的漂移误差,仅依靠里程计与惯导进行组合会降低整个定位方法的测量精度。文献[5]采用联邦滤波将惯性测量单元(IMU)分别与立体相机、里程计构成子滤波器,避免了因里程计打滑或滑移失效产生的较大测量误差污染整个定位系统[6],但井下视觉定位方法目前还处于理论研究阶段,未出现成功应用的工业性案例,故其可实施性与可靠性均属未知。文献[7]采用集中式滤波处理惯性导航系统、里程计及测距雷达所获取的各类传感器的测量信息,在进行卡尔曼滤波状态方程建模时维数较高,整个系统计算量较大且容错性差。
综上可知,目前多采用里程计、视觉测量、测距雷达等作为辅助测量方式,与惯导组合测量降低惯导随时间累积所产生的位置漂移误差,其中辅助测量方式要求可靠性与测量精度均较高。对不同测量方式得到的数据目前多使用集中式卡尔曼滤波进行滤波解算,但集中式卡尔曼滤波的计算量较大且容错性较差。针对上述问题,本文提出了一种由捷联式惯导、测距雷达及里程计组成的连续采煤机定位方法,使用测距雷达与里程计测量连续采煤机的位移量,通过航位推算法推算出机身的二维位置信息,利用二维位置信息对惯导位置解算信息进行反馈修正,减小惯导随时间累积所产生的位置漂移误差[8]。采用联邦式卡尔曼滤波对各传感器采集的位姿信息进行滤波与融合[9-11],通过降低方程维数减少计算量,在保证精度的同时还具备一定的容错性。该定位方法可为连续采煤机在巷道约束环境下的位姿精确测量、巷道自动成形控制和远程控制奠定基础。
1 连续采煤机定位方法
连续采煤机定位方法结构组成如图1所示。使用测距雷达与里程计同时辅助修正惯导系统,采用联邦式卡尔曼滤波将惯导分别与测距雷达、里程计组成子滤波器。在里程计因履带打滑或滑移产生较大的测量误差时,提高测距雷达与惯导所组成的子滤波器1的置信度;在测距雷达因人员移动或其他障碍物遮挡而导致测量误差较大时,里程计及惯导所组成的子滤波器2采取较高的置信度,防止因个别辅助传感器测量失效产生较大误差而降低定位方法的精度。

1-连续采煤机本体; 2-惯导组件; 3-电控箱; 4-里程计;
1.1 惯导系统
惯导系统根据安装方式可分为平台式与捷联式,根据所采用的陀螺仪种类不同又可分为光纤级、激光级等[12]。本文采用某型号光纤级捷联式惯导,惯导本体及交换机直接固连于连续采煤机机身中部右侧位置,紧邻电控箱,可实时测量机身的姿态、速度及位置信息。该定位方法取测距雷达、里程计与惯导系统所推算得到的机身位置信息差值作为滤波输入来进行滤波处理[13],各传感器所采集到的位姿信息可通过交换机传送至巷道后方安全位置或地面控制室内的上位机进行显示与控制。
1.2 测距雷达
测距雷达安装于连续采煤机机身尾部右后下方,将规格为1 m×1 m的标靶放置于与测距雷达处于同一水平线的正后方。连续采煤机行进过程中通过测距雷达不断测量与后方标靶的距离,所得的当前测量值与前一次采样频率下的测量值作差便可得到连续采煤机的相对位置增量。利用航位推算法对相对位置增量进行解算便可得到机体坐标系下的位置信息,借助惯导解算中的姿态矩阵实时地将机体坐标系下的位置信息转换为导航坐标系下的信息后再进行滤波解算[14]。
1.3 里程计
里程计安装于履带驱动齿轮处,输出量为连续采煤机短时间内路程增量,通过航位推算法得出所需要的位置信息[15]。里程计由于固连于车体履带转轴处,所测得的信息量依旧是在机体坐标系下的,同样需借助惯导解算中的姿态矩阵实时地将其转换为导航坐标系下的信息量后再进行滤波解算。
2 航位推算法
航位推算法是一种使用航向和里程信息来计算运载体相对于起点的相对位置的定位方法,原理如图2所示。已知起始位置坐标(x0,y0)及起始方位角θ0,通过测量行驶距离Si及方位角变化值Δθi,结合二者值便可推算出下一时刻位置坐标(xk,yk)和方位角θk。
(1)
(2)
θk=θk-1+Δθk-1k=1,2,…
(3)
式中:θk-1为上一时刻方位角,k为不同时刻;Δθk-1为上一时刻至当前时刻方位角变化。

图2 航位推算法原理Fig.2 Principle of dead reckoning algorithm
3 滤波器模型构建
3.1 联邦式卡尔曼滤波原理

(4)
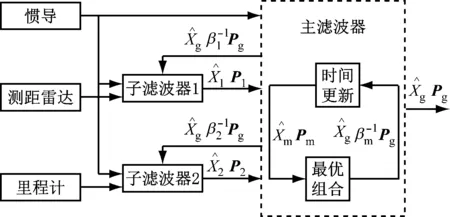
图3 联邦式卡尔曼滤波器原理Fig.3 Federated Kalman filter principle

为了简化计算,在信息分配上,使用平均分配方式分配子滤波器与主滤波器间的方差矩阵值,即
βj=βm=1/3
(5)
3.2 误差分析
定位方法中的误差主要来源于捷联惯导自身器件误差及算法更新误差、里程计及测距雷达测量误差,通过误差分析可为滤波器建模奠定基础。
3.2.1 惯性导航误差

其中关于捷联式惯导更新算法中的姿态、速度及位置误差推导见文献[16]。
3.2.2 测距雷达测量误差
测距雷达测量误差主要为自身固有误差δρ及初始输入误差δη。经分析这2类误差特性,同时为简化模型及降低计算量,将其设置为固定常值对误差进行补偿,以消除其对实验结果的影响。故在后续建模过程中,将测距雷达这2类误差均设为固定常值。
3.2.3 里程计测量误差
里程计的测量误差主要包括标度因数误差δKD和安装误差角δα,设δα=[δαθδαγδαψ],δαθ,δαγ和δαψ分别为安装角误差中的俯仰角、横滚角和航向角误差。其中里程计的横滚角安装误差一般不会对测距雷达的位置输出量造成干扰,故这里不考虑横滚角安装误差。俯仰角安装误差及航向角安装误差对里程计测量误差有影响,将δKD、δαθ、δαψ三者均设为随机常值。
3.3 滤波器模型构建
联邦式卡尔曼滤波作为卡尔曼滤波的变式,其与集中式卡尔曼滤波的区别在于联邦式卡尔曼滤波子滤波器先进行一级滤波,而后进入联邦式卡尔曼滤波主滤波器进行二级滤波,同时将全局滤波最优估计及误差方差矩阵放大后反馈给子滤波器进行下一次滤波[18-19]。
2个子滤波器均采用间接法进行卡尔曼滤波器数学建模,即状态变量由导航参数的误差构成,同时对该连续变量信息进行离散化,以便于卡尔曼滤波进行分步迭代更新[20],本文为描述简便直接给出离散化后的数学模型。
3.3.1 子滤波器1数学模型
状态方程为
Xk1=Φk1/k1-1Xk1-1+Γk1-1Wk1-1
(6)
式中:Φk1/k1-1为子滤波器1的十五维状态转移矩阵;Γk1-1为子滤波器1的噪声驱动矩阵;Wk1-1为子滤波器1的陀螺与加速度计的白噪声矩阵。
状态向量为

(7)

量测方程为
Zk1=Hk1Xk1+Vk1
(8)
式中:Zk1为子滤波器1以惯导与测距雷达所输出的位置量作差得到的观测量;Hk1为子滤波器1的量测矩阵;Vk1为子滤波器1的测距雷达的位置量测白噪声矩阵。
3.3.2 子滤波器2数学模型
状态方程为
Xk2=Φk2/k2-1Xk2-1+Γk2-1Wk2-1
(9)
式中:Φk2/k2-1为子滤波器2的二十一维状态转移矩阵;Γk2-1为子滤波器2的噪声驱动矩阵;Wk2-1为子滤波器2的陀螺与加速度计的白噪声矩阵[20]。
状态向量为

(10)

量测方程为
Zk2=Hk2Xk+Vk2
(11)
式中:Zk2为观测量,子滤波器2以惯导与里程计根据航位推算法推算出的位置量作差作为观测量;Hk2为子滤波器2的量测矩阵;Vk2为子滤波器2的里程计的位置量测白噪声矩阵。
4 仿真
为检验连续采煤机定位方法的定位精度及2类卡尔曼滤波的容错性,本文进行了Matlab 仿真实验。仿真时长取20 min即1 200 s,模拟连续采煤机实际掘进过程中不停机生产时长。在仿真时间为5 min即300 s时加入里程计测量误差扰动,持续时间为30 s,模拟连续采煤机打滑情况。惯导关键精度参数设置:陀螺仪的常值漂移εb设置为0.001 °/h, 加速度计零偏设置为1×10-4g(g为重力加速度)。
4.1 姿态误差
集中式与联邦式卡尔曼滤波航向角误差对比如图4所示。从图4可看出,在前200 s 时,2类滤波波动均较大,其中集中式卡尔曼滤波最大波动可达10′。在200 s后,2类滤波的滤波值逐渐趋于平稳,在0~-2.5′内小幅波动。在300 s时加入里程计测量误差扰动后,与联邦式卡尔曼滤波相比,集中式卡尔曼滤波出现的突变值较大,最大可达-8′,且在30 s内加入误差的过程中持续出现突变值,而联邦式卡尔曼滤波出现突变后,短时间内便恢复至正常滤波值范围。

图4 航向角误差对比Fig.4 Comparison of heading angle error
集中式与联邦式卡尔曼滤波横滚角误差对比如图5所示。从图5可看出,在前80 s时,2类滤波的滤波值波动均较大,集中式卡尔曼滤波波动范围更大,最高可达14′;在80 s后,2类滤波的滤波值恢复至-1~1′内波动。在300 s时加入里程计测量误差扰动后,2类滤波均出现了瞬时突变,但联邦式卡尔曼滤波突变值较小且持续时间较短,且在较短时间内恢复到了正常值。

图5 横滚角误差对比 Fig.5 Comparison of roll angle error
集中式与联邦式卡尔曼滤波俯仰角误差对比如图6所示。从图6可看出,在滤波初期240 s内,2类滤波的滤波值波动均较大,且与航向角、横滚角相比,波动峰值更大,最大处可达270′。在240 s后,滤波波动值稳定于15′附近。在300 s时加入里程计测量误差扰动后,与前2个姿态角波动相类似,集中式卡尔曼滤波产生的瞬时突变值较大且持续时间长,而联邦式卡尔曼滤波则可以在短时间内恢复至正常波动范围内。
由3个姿态角误差可得出,误差角在滤波稳定后可达到角分级,天向通道中的俯仰角误差在前期滤波过程中波动较大,最大波动值可达270′,稳定后在15′内波动;东向通道中的航向角和北向通道中的横滚角仿真误差值较小,稳定后波动值为2.5′左右。注入里程计测量误差扰动后,与集中式卡尔曼滤波相对比,联邦式卡尔曼滤波出现的瞬时波动值较小且持续时间短,容错能力更强。

图6 俯仰角误差对比 Fig.6 Comparison of pitch angle error
4.2 位置误差
集中式与联邦式卡尔曼滤波经度误差对比如图7所示。从图7可看出,在300 s时加入里程计测量误差扰动后,集中式卡尔曼滤波较联邦式卡尔曼滤波出现的瞬时波动值更大且持续时间更长,可达30 s,与注入里程计扰动时长相符。待稳定后,2类滤波的波动值为-1~1 cm。
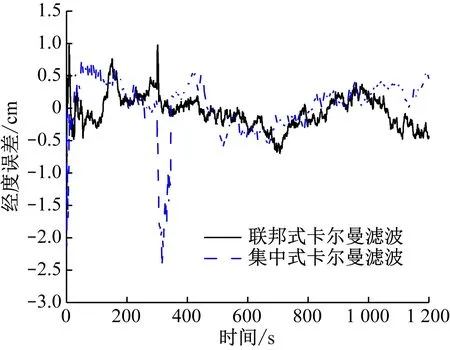
图7 经度误差对比 Fig.7 Comparison of longitude error
集中式与联邦式卡尔曼滤波纬度误差对比如图8所示。从图8可看出,在300 s时加入里程计测量误差扰动后,2类滤波均出现了相应波动,其中集中式卡尔曼滤波的波动值较大且持续时间较长,滤波稳定后,2类滤波的波动值为-0.5~0.5 cm。
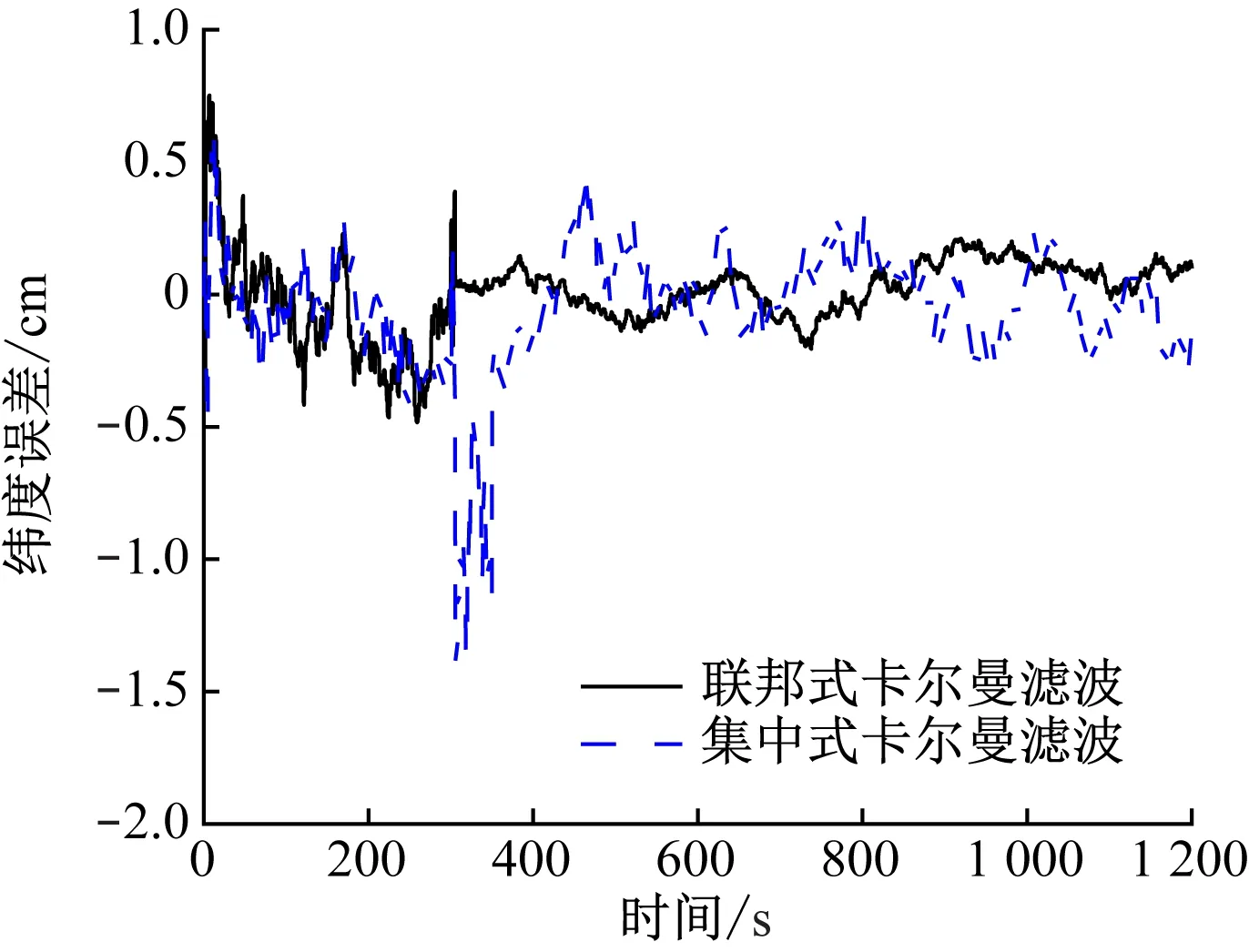
图8 纬度误差对比Fig.8 Comparison of latitude error
集中式与联邦式卡尔曼滤波高度误差对比如图9所示。从图9可看出,在300 s时加入里程计测量误差扰动后,集中式卡尔曼滤波出现了较大瞬时波动值,最高达-4.5 cm,且波动持续时间较长,滤波稳定后,2类滤波的波动值为-2~2 cm。

图9 高度误差对比Fig.9 Comparison of height error
由上述分析可得出,位置误差在滤波稳定后可达厘米级精度,天向通道的高度误差相较于经纬度误差较大,达到10 cm,稳定后在-2~2 cm内波动。经度误差稳定后为-1~1 cm,纬度误差稳定后为-0.5~0.5 cm。与姿态误差最终结果表现相同,联邦式卡尔曼滤波在加入误差扰动后出现的瞬时波动值较小且持续时间短,容错能力强。
5 结论
(1) 使用捷联式惯导、里程计及测距雷达组合测量,可实现煤矿井下连续采煤机较高精度的位姿信息获取。
(2) 通过测距雷达与里程计共同进行位置推算辅助修正捷联惯导系统,可有效抑制惯导随时间积累所产生的位置漂移误差。
(3) 联邦式卡尔曼滤波与集中式卡尔曼滤波相比,2类滤波在精度基本一致的前提下,联邦式卡尔曼滤波在受到较大测量误差干扰后出现的瞬时波动值小且波动时间短,具备一定的容错性。
(4) 采用联邦式卡尔曼滤波的定位方法的定位精度可达±2 cm,定向精度可达15′,可靠性较高,抗干扰能力较强,可为下一步井下现场试验提供理论与实验依据。
DOI:10.3390/s19173812.
DOI:10.3390/s17020239.

