基于R2-MOEA/D算法的顶板支护决策模型

郝秦霞， 汪连连， 张金锁

(1.西安科技大学 通信与信息工程学院, 陕西 西安 710054；2.西安科技大学 安全科学与工程学院, 陕西 西安 710054;3.西安科技大学 能源经济管理研究中心， 陕西 西安 710054;4.延安大学 经济与管理学院， 陕西 延安 716000)

0 引言

在矿井深部开采中，顶板来压会造成岩层裂变，严重影响矿井安全生产[1]。顶板来压受顶板强度、底板强度、煤体强度等多条件指标影响，因此，需要根据实际情况分析指标特征，建立顶板支护案例库，并对顶板来压的条件指标和结果属性进行形式化定义，以节省存储空间。为了实现顶板支护决策多指标的最优化，可以使用高维多目标优化算法对各项指标进行优化，构建巷道支护决策方案。

国内外许多学者对煤矿顶板安全支护决策进行了研究，并取得了一定的成果。I.Shafii等[2]提出了CMRR(Coal Mine Roof Rating)指标，用于对顶板单元的水分敏感性、轴向强度和径向强度进行表征。J. Coggan等[3]对水平应力与煤矿顶板之间的关系进行了数值模拟计算。王志强等[4]根据侧帮锚杆作用机理提出了联合支护技术。侯朝炯等[5]提出了深部巷道破裂围岩浅孔封隙止浆和深孔减隙加固的注浆技术,使用该技术后巷旁充填体表面位移降低了38%,围岩应力降低了17.9%,水平应力偏移了60°。王志强等[6]采用FLAC3D数值模拟软件研究分析了上区段沿顶巷道侧帮锚索参数对侧向煤体应力分布和力学性质的影响,确定了合理的侧帮锚索和沿底巷道顶板支护参数。薛黎明等[7]通过二维云发生器绘制出了围岩稳定性分级的二维云图，并通过Apriori算法进行关联挖掘，得到了围岩稳定性的综合等级决策表，建立了围岩稳定性的岩体及地质因素和工程因素二维分级指标体系。刘海雁等[8]采用正交数值模拟方法设置影响巷道稳定性的锚杆长度、顶角锚杆安装角度和预紧力的影响权重分别为51.7%,45.8%和2.5%，采用所提方法得到的优化支护方案应用效果良好。冯友良等[9]基于RSM-BBD试验设计与离散元法研究了巷帮失稳关键因素及其控制技术,实验结论表明单一因素及其各自之间交互作用都会影响巷帮稳定性，并且RSM-BBD试验设计与离散元法可显著改善巷帮煤体失稳问题。煤矿顶板支护系统已有初步模型[10]，但现有的支护方法效果却不尽如人意，主要存在以下问题：

(1) 顶板来压受复杂因素的相互影响、相互制约，现有决策方法或片面分析安全因素，或引用专家意见，或对指标客观赋予权重，不同指标对顶板事故的影响程度未能分配有效的权重系数。

(2) 顶板案例库涉及事故指标多样，进行案例决策属于高维多目标问题，而现有决策结果不能满足实际需求。

针对以上问题，笔者对顶板来压的指标进行分析，构建了基于R2-MOEA/D算法的顶板支护决策模型，并进行了案例相似度计算，为顶板事故快速决策提供有效方法。

1 顶板来压指标选取

以《煤矿支护手册》设定的巷道支护形式与参数选择为基础，结合《回采巷道支护形式与参数合理选择专家系统》建立顶板来压指标知识库M，见表1。M={m1,m2,…,mn}，mi(i=1,2,…,n，n为指标个数)表示案例的第i个指标。顶板指标知识库M包含顶板来压条件指标和结果属性2个部分，事故案例是以条件指标作为判断依据，以结果属性作为顶板支护方案。在案例决策中匹配相似度最高的案例时，仅以条件指标值作为多目标决策的相似度计算依据，将匹配相似度最高的条件指标值所对应的结果属性值作为顶板支护方案。

表1 顶板指标知识库MTable 1 Roof index knowledge base M

2 基于R2-MOEA/D算法的顶板支护决策模型构建

2.1 模型构建

为实现顶板支护案例决策结果的最优化，首先利用层次分析法和熵值法对知识库中的条件指标进行计算，分别得到指标的主观权重和客观权重，在确定主观、客观权重的基础上引入离差函数，得到各项指标的混离差权重；接着优化差分进化算法，提出R2-MOEA/D算法，应用切比雪夫公式将多目标问题分解成多个子问题，每个子问题在邻域范围内交叉、变异，利用切比雪夫函数作为R2指标排序标准来进行个体选择，得到收敛性和多样性[11-12]较好的Pareto最优解，即相似度最高的条件指标顶板案例，其对应的结果属性为事故案例的决策提供了支护方案。基于R2-MOEA/D算法的顶板支护决策模型的整体流程如图1所示。

2.2 权重分配

条件指标权重一般是通过客观权重或主观权重确定，但客观权重未根据实际情况考虑现场专家的意见，主观权重仅考虑专家意见，未考虑以往的历史经验。因此，本文在此基础上引入离差函数来平衡主观、客观条件指标值，得到指标的综合权重。综合权重算法步骤如下：

(1) 通过熵值法得到指标的客观权重，熵值越小，信息的不确定性也就越小，权重越大。第i个条件指标的权重vi的计算公式为

(1)

(2)

图1 基于R2-MOEA/D算法的顶板支护决策模型流程Fig.1 Flow of decision model of roof support based on R2-MOEA/D algorithm

(3)

(2) 利用层次分析法求得条件指标的主观权重[13]，构造判断矩阵A，判断矩阵A由api构成，api为第p(p=1,2,…,P,P为专家人数)个专家对第i个指标赋予的权重, 按照《数值的设定标准群》[13]构造，计算一致性比例CR，当CR小于0.01时，CR的最大特征值γmax对应的特征向量ui就是指标的权重值。CR计算公式为

(4)

(5)

(6)

式中RI为平均随机一致性指标，可通过查询表2获得。

表2 RI数值Table 2 RI values

为了充分考虑主观、客观因素，将熵值法和层次分析法得到的权重引入离差信息得到条件指标的综合权重：w={w1,w2,…,wn}，wi表示第i个条件指标的权重。综合权重与主观、客观权重总的离差和最小，说明主观、客观因素考虑越充分，因此构造混合离差函数模型：

(7)

式中μ表示离差函数的偏好因子，为主观权重占比，(1-μ)为客观权重占比。

2.3 R2-MOEA/D算法

R2-MOEA/D算法利用非支配解指导种群的进化，首先在目标空间中随机产生h个初始种群{x1,x2,…,xh},并生成N个均匀分布参考权重向量λ，λ∈[0,1]，根据R2-MOEA/D算法对父代种群进行变异、交叉等一系列操作，产生子代种群，将子代种群与父代种群合并，在合并种群中，引入R2指标进行环境选择，利用R2贡献值进行R2排序，从合并种群中选择h个个体x进入下一代，进行多次迭代后或者满足算法结束条件后所得到的的解就为最终的顶板支护决策方案，即相似度最高的条件指标顶板案例所对应的结果属性值，其详细步骤如下：

(1) 首先在目标空间中随机产生h个初始种群X={x1,x2,…,xh},并生成N个均匀分布参考权重向量λ，引入切比雪夫公式，将高维多目标优化问题分解成多个单目标子问题。切比雪夫公式为

subject tox∈Ω

(8)

(2) 利用欧氏距离选取距离权重向量最近的T个权重向量,D(d)={d1,d2,…，dT}，随机从D(d)中随机选取2个序号k,l作为父代种群,利用遗传算子产生一个新解y为子代,并将子代与父代进行合并，引入R2指标来判定2个个体x1,x2的优劣，计算个体的R2贡献值，保留R2贡献值较大的个体进入下一代循环，保证种群的数目为h，以便引导种群的进化。

个体x1的R2指标公式为

R2(x1,λ,w*)=

(9)

个体x1的R2的贡献值为

CR2(x1,λ)=R2(x1,λ,w*)-R2(X/{x1},λ,w*)

(10)

(3) 将最优解w*对应的wi代入相似性公式中进行全局搜索，得到相似度最高的条件指标顶板案例。相似性公式为

(11)

3 实验与结果分析

3.1 评价指标

为了检验R2-MOEA/D算法的性能，本文使用目前主流的NSGA2、NSGA3、RVEA算法分别与R2-MOEA/D算法进行收敛性和多样性的分析，评价方法选择了GD(Generational Distance，世代距离)和IGD(Inverted Generational Distance，反转世代距离)[16]。将收敛性和综合性作为评价标准，GD用于检验算法在优化过程中种群收敛的能力, 表示解集中的每个点到参考集中点的平均最小距离，GD值越小，说明收敛性越好。IGD表示每个参考点到最近解的距离的平均值，IGD值越小，说明算法综合性能越好，整体效果更好。

3.1.1 测试函数

DTLZ1—DTLZ7是用于评价高维MOEAs性能最广泛的测试集之一,目标个数可以任意设置,并且具有线性、凸凹面、多峰性、退化性及连续、非连续性等特征[17]，因而，实验采用DTLZ1—DTLZ7进行算法对比分析。在一个给定的M目标测试中，测试问题划分为4,5,8,10,15目标时,即m∈{4,5,8,10,15}，为保证算法的公正性，按照文献[18]对实验参数进行设置。

3.1.2 结果对比分析

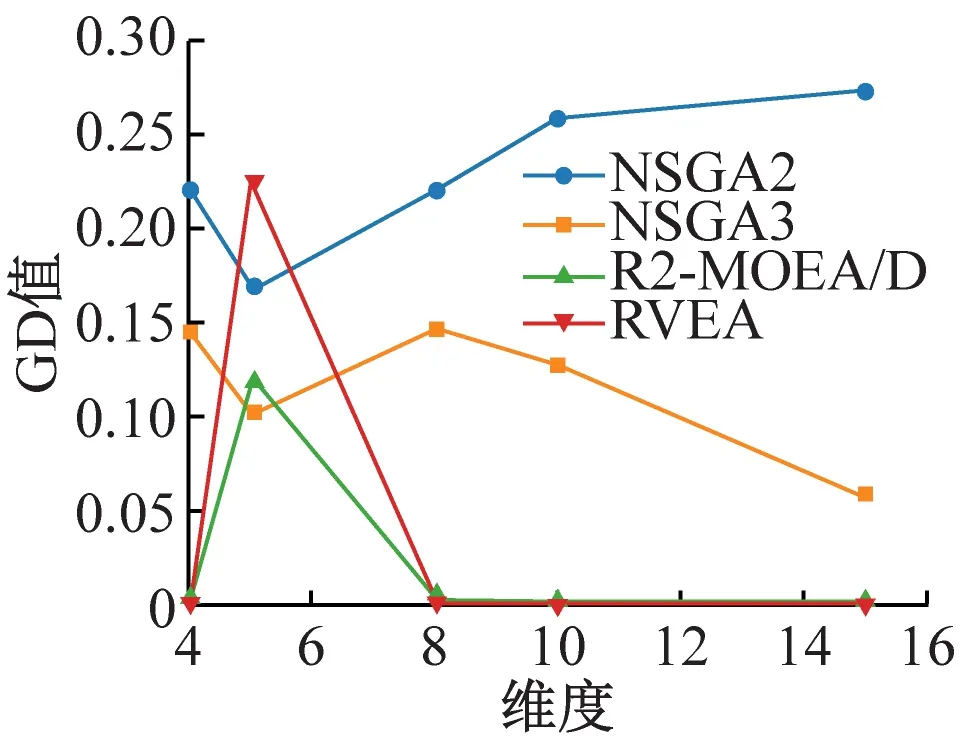
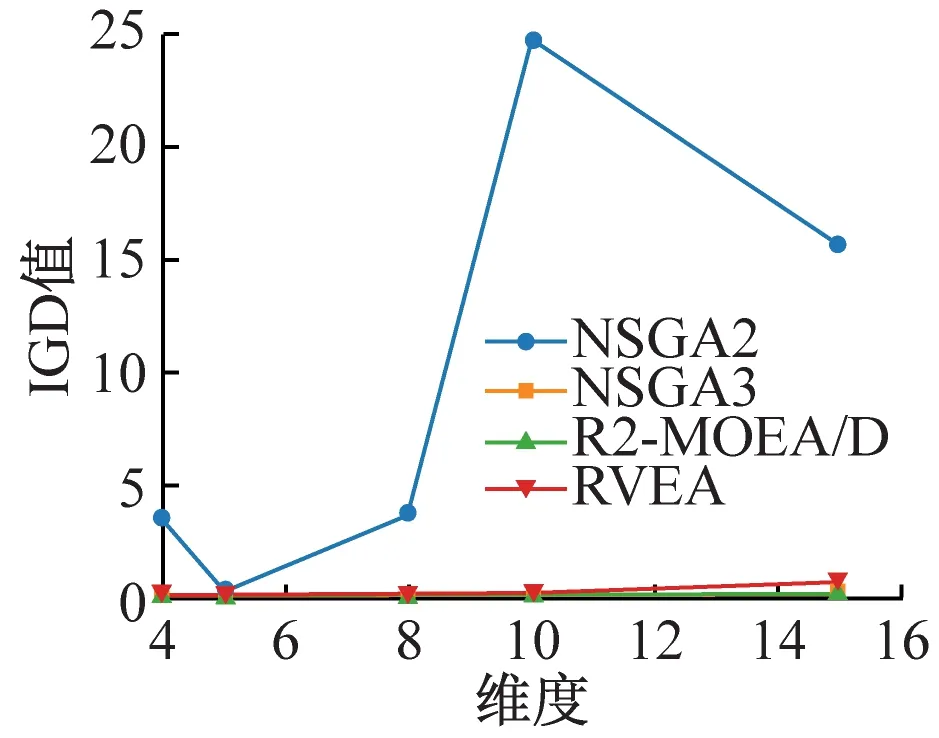
为了直观地比较各算法的性能，在4,5,8,10,15维下，采用测试函数DTLZ1—DTLZ7,将NSGA2,NSGA3,RVEA算法与R2-MOEA/D算法进行对比，其GD值、IGD值比较如图2、图3所示。

(a) DTLZ1

(e) DTLZ5

(a) DTLZ1

(e) DTLZ5

从图2可看出，在测试函数DTLZ1—DTLZ7上,随着维度的增加，NSGA2、NSGA3、RVEA算法的GD值也不断增加，算法的收敛性能降低，R2-MOEA/D算法的GD值随着维度的变化而缓慢变化，其GD值在同一维度下的同一测试函数上低于其他3种算法，并且当测试函数为DTLZ1、DTLZ5、DTLZ7时，R2-MOEA/D算法在10,15维上的GD值最小，其数据的收敛性最优，在维度为5时，其性能仅次于最优；当测试函数为DTLZ2、DTLZ3、DTLZ4和DTLZ6时，R2-MOEA/D算法在5,10,15维上拥有最小的GD值，其数据的收敛性最优。总体来看，R2-MOEA/D算法的收敛性能优于其他3种算法。

从图3可看出，在测试函数DTLZ1—DTLZ7上，随着维度的增加,NSGA2、NSGA3、RVEA算法的IGD值也不断增加，算法的收敛性和多样性降低。R2-MOEA/D算法的IGD值随着维度的变化而缓慢变化，并当测试函数为DTLZ1、DTLZ3、DTLZ5、DTLZ6时，R2-MOEA/D算法在5,10,15维上IGD值均最小，表明R2-MOEA/D算法的多样性表现最优；当测试函数为DTLZ2时，R2-MOEA/D算法在10,15维上有最小的IGD值，当数据维度为5时，NSGA3算法有最小IGD值，算法的多样性最优，R2-MOEA/D算法仅次于NSGA3算法；当测试函数为DTLZ4和DTLZ7时，R2-MOEA/D算法性能稍差，其IGD值与最小IGD值相差不大。总体来看，R2-MOEA/D算法的性能优于NSGA2、NSGA3和RVEA算法。

3.2 实例分析

通过山西霍州矿区三交河煤矿2-6011巷道和10-4151巷道来综合评定模型的可行性。具体建模步骤如下：

(1) 收集来自山西霍州矿区三交河煤矿、辛置煤矿、李雅庄煤矿，河北邯郸矿业云驾岭煤矿，山西汾西矿业新柳煤矿的地质信息，提取其中的条件指标数据和结果属性指标数据[19]，构建顶板支护知识库，采用R2-MOEA/D算法对条件指标进行组合赋权并进行知识库案例检索，得到适合当前案例的解决方案。

(2) 通过熵值法得到各条件指标的权重,见表3。

(3) 通过层次分析法得到各条件指标的权重,见表4。

(4) 引入R2-MOEA/D算法对综合权重进行优化并检索出适合当前案例的解决方案，通过选取R2-MOEA/D中的6条最优解得到各指标的权重，见表5。

表3 熵值法指标权重Table 3 Index weight of entropy method

表4 层次分析法指标权重Table 4 Index weight of AHP

表5 R2-MOEA/D指标权重Table 5 Index weight of R2-MOEA/D

(5) 选取R2-MOEA/D权重的第1行，即当主观权重与客观权重所占整体权重的比例为0.590 5∶0.409 5时所得到的综合权重，利用R2-MOEA/D算法得到2-6011巷道和10-4151巷道的支护方案，见表6、表7。

将所得支护方案与实际支护情况比较可知，由R2-MOEA/D算法检索出的解决方案符合当前案例的支护情况，证明了基于R2-MOEA/D算法的顶板支护决策模型的可行性。

表6 2-6011巷道锚杆支护情况Table 6 Bolt support of 2-6011 roadway m

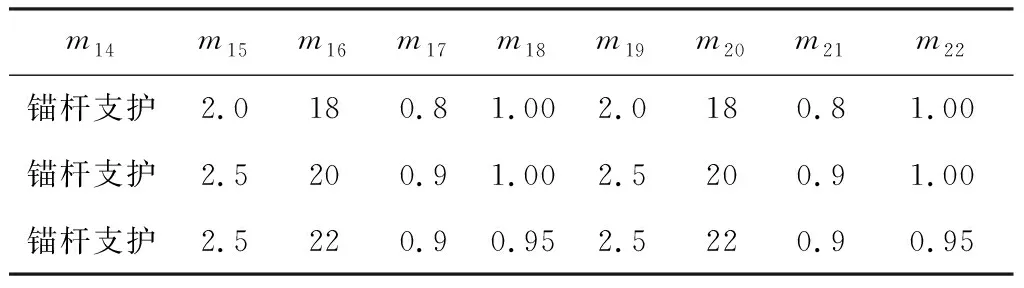
表7 10-4151巷道锚杆支护情况Table 7 Bolt support of 10-4151 roadway m

4 结论

(1) 提出了一种基于R2-MOEA/D算法的顶板支护决策模型。首先对顶板来压的指标进行分析，构建顶板指标知识库，使用熵值法确定客观权重，层次分析法确定主观权重；然后为平衡主观、客观权重对指标选择的影响，引入离差函数设计混离差权重矩阵，差分高维多目标进化算法，在引入混离差权重后，对高维多目标问题进行分解，对进化算子进行交叉、变异；最后利用R2指标对结果集进行排序，得到收敛性与多样性分布较好的Pareto解集，即匹配度高的实时顶板支护决策方案。

(2) 回采巷道支护方式受许多因素影响，而不同因素对支护效果影响不同，通过组合赋权法，引入离差函数确定指标权重，综合考虑客观因素和主观因素的影响，能够给每个条件指标赋予不同的权重，使不同条件指标对煤矿回采巷道支护效果的影响占据不同的权重，使实验结果更加合理准确。

(3) 将R2-MOEA/D算法与NSGA2、NSGA3、RVEA算法进行比较，使用GD值和IGD值对收敛性和多样性进行评判，结果表明:R2-MOEA/D算法能够得到更优的Pareto解集。

(4) 在案例检索时，使用R2-MOEA/D算法计算其适应度值，在全局范围内检索满足适应度条件的解决方案，通过三交河煤矿2-6011巷道和10-4151巷道对基于R2-MOEA/D算法的顶板支护决策模型进行可行性评定，结果表明：该模型可根据顶板指标建立实时、有效的顶板支护决策方案，由R2-MOEA/D算法检索出的解决方案能够符合目标案例的支护情况，证明了该模型的可行性。

DOI：10.18637/jss.v092.i06.