一类生态系统模型食物链研究
夏 鹏,李 旭
1.江苏联合职业技术学院无锡旅游商贸分院,江苏无锡,214045;
2.浙江理工大学科技与艺术学院,浙江绍兴,312369
通过数学模型研究生态系统各种复杂的现象一直是热门的研究课题[1-2]。为了更好优化整合生态资源,Liu[3]在2009年建立了如下的生态数学模型:
(1)
其中,模型(1)中(x,t)∈Ω×R+,对于(x,t)∈∂Ω×R+边界条件为:
(2)
初始条件为:
(3)
1 理论分析
本节主要讨论扩散速率、死亡率、转化率和趋化系数对稳态下微生物种群分布会产生怎样的影响。因为处理好各参数与微生物种群之间的关系,可以更好地帮助我们从理论依据上去保护生态系统。在数学上,我们建立当k=2时,系统(1)—(3)定态解存在性和稳定性条件。在一维条件下,即Ω=(0,l),其中l为正实数,那么系统重新写作下列模型:
(4)
边界条件和初始条件分别写为:
(5)
且N0(x)>0,w10(x)>0,w20(x)>0。
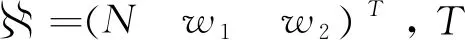
(6)
在一维区间[0,l]上带有诺依曼边界条件的负拉普拉斯算子特征值问题[6]:

那么上述线性系统(6)中Λm等价写成下列矩阵形式:
(7)
(8)
因此,由特征值稳定性理论分析[7],我们有下面结果:
命题1因为线性系统t=Λ0有主特征值λ0=1-d0μ0=1,那么定态解E0总是不稳定的,即系统(4)至(5)是持久的。
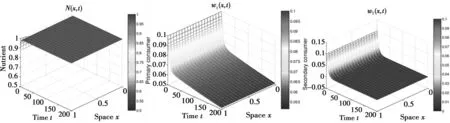
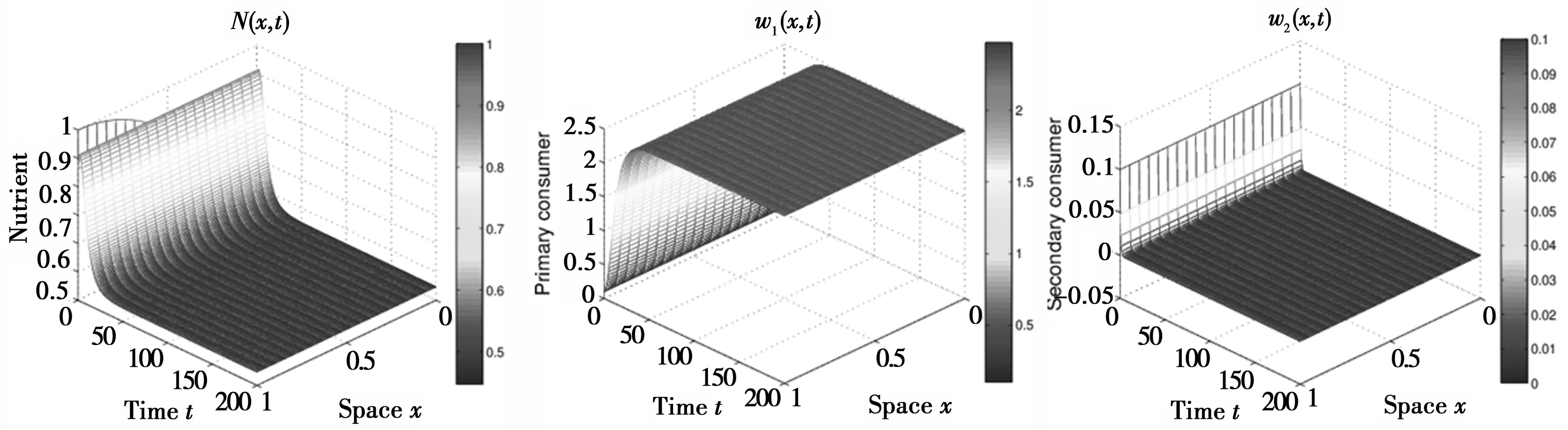
命题2如果γ1 命题3如果γ1>b1,那么线性系统t=Λ1有一个特征值λ0=γ1-b1>0,因此,特征值E1是不稳定的。那么系统(4)至(5)食物链长度大于1,即p≥2。 本节我们将通过MATLAB中PDE工具包来数值仿真研究系统参数如何影响系统(4)至(5)种群存在性[8],其中边界条件为(5)式,初始条件取 w10(x)=w20(x)=5 (9) 事实上,只要初始条件满足(5)式中条件,有相同的结果。故可以得到下列结论。 结论1当死亡率bi和转化率γi固定,即使改变扩散系数和所有趋化参数值,具有边界条件(5)和初始条件(9)的系统(4)也会进入相同的定态,这表明扩散和趋化性不会影响所考虑系统的定态,这与理论结果相符。因此令d0=d1=d2=1,且σ1=σ2=c1=c2=1。 结论2假设死亡率固定为b1=0.1,b2=0.2,将具有边界条件(5)和初始条件(9)的系统(4)中转化率γ1,γ2设为不同值。发现: (1)当γ1>b1,γ2>b2时,这三个生物种群共存于这个封闭区域。即食物链长度p=3。而且令γ2≥γ1,那么当γ1与γ2值差别越大时,这三个生物种群密度呈周期状演化越明显(图1—图3)。 (2)通过尝试各种参数值,当γ1≤b1,那么三个生物不可能共存。因为从现实生活中也容易知道当初级消费者营养转化率小于死亡率时,初级消费者数量会锐减,营养不会向下一级传递,所以不可能共存。这个现象也可以观察比较图1和图4。其中图4食物链长度为2。这些数值结果与命题1—3极为一致。 结论3当营养转化率保持固定,比较图1和图5,其中图5食物链长度为1,如果我们改变死亡率b1,使得b1≥γ1,那么初次消费者将要灭绝,则在封闭区域内,二级消费者无论营养转化率γ2取多大,由于缺乏食物,它们也不能存活。然而假设b1≤γ1,但是b2>γ2且足够大,那么初级消费者可以演变到正常数而二级消费者往往会灭绝。这可以比较图1和图6,其中图6食物链长度为2,这些仿真也证实了命题1—3。 图1 生物种群密度变化图(b1=0.1,b2=0.2,γ1=0.25,γ2=6) 图2 生物种群密度变化图(b1=0.1,b2=0.2,γ1=1,γ2=6) 图3 生物种群密度变化图(b1=0.1,b2=0.2,γ1=0.5,γ2=0.6) 图4 生物种群密度变化图(b1=0.1,b2=0.2,γ1=0.1,γ2=0.6) 图5 生物种群密度变化图(b1=0.25,b2=0.2,γ1=0.25,γ2=6) 图6 生物种群密度变化图(b1=0.1,b2=1.5,γ1=0.5,γ2=0.6) 在这项工作中,我们给出了理论分析和数值计算,为了展示系统参数是如何影响具有自产营养的封闭生态系统的食物链。结果表明,在所考虑的模型中,扩散和趋化对系统没有产生影响。但是,食物从低层到高层的转化率γi,(i=1,2,3…)即第i种微生物的消费能力对生物体的共存及其生存方式起着至关重要的作用。因此,对自然界生态系统维持共存提供了一定的理论基础。2 数值研究




3 结束语

