基于检测与跟踪相互迭代的极暗弱目标搜索算法
効 琦,尹增山*,高 爽
(1.中国科学院微小卫星创新研究院,上海 201203;2.上海科技大学信息科学与技术学院,上海 201210;3.中国科学院大学,北京 100049)
0 引言
暗弱运动小目标的检测在控制制导、轨道规划等航空航天的应用[1-3]中是极为关键的技术。在目标检测[4]算法中,由于运动目标的小型化、高速化以及对更大范围检测的进一步要求,使得成像的小目标像素数量极少,图像信噪比(Signalto-Noise Ratio,SNR)极低。此时暗弱小目标被强噪声干扰,信息量不足导致二者难以区分。
在目标检测中可以利用目标的两种信息:一是运动学特征,包括速度、方向和距离等;二是视觉特征,主要有纹理、颜色、尺寸和外形。暗弱目标,即只有运动学特征的信息可以利用的目标,所以基于利用视觉信息的帧差法[5]和三帧差法不适用于暗弱目标检测,并且背景差分法[6]也会由于SNR 极低的原因无法分辨目标与构建的背景之间的差异,效果不理想。另外,利用单帧空域信息的目标检测算法也需要视觉特征的信息[7]。近年来基于时空联合[8]和时频分析[9-11]的各种检测算法被学者们不断提出。这些算法利用了连续数帧的时域信息,可以检测大约SNR 为3 dB 左右的目标,满足绝大多数弱小目标的检测任务。文献[12]提出了一种基于时域高阶的运动点目标检测方法,该方法将其定义为基于双谱均值和标准差的多变量测试问题。对于极低信噪比(extremely Low Signal-to-Noise Ratio,LSNR)的暗弱目标,检测前跟踪(Track Before Detect,TBD)[13]是目前比较流行的一种方法。TBD 算法利用目标在时域序列中的连续性,挑选和累积疑似轨迹,最后选中轨迹真实性最高的目标。不过TBD 计算复杂度极高,尤其在视频尺寸大或者帧数多时更为严重。为降低计算复杂度,基于动态规划(Dynamic Programming,DP)的TBD 算法DP-TBD 算法[14-15]被提出。传统的目标检测算法由于需要目标的视觉信息,无法检测暗弱小目标。基于时空联合、时频分析的方法和TBD 没有充分挖掘目标的时域信息,只用数帧或者低帧率的图像做检测存在一定的局限性。
要解决对LSNR 目标的检测问题,首先要从增加目标的先验信息考虑,可从提升空间分辨率和时间分辨率两方面考虑,增加在成像过程中暗弱小目标的信息量。由于星载或机载摄像机载荷的限制,相较于增加镜头直径,选择具有更高采集速率的互补金属氧化物半导体(Complementary Metal Oxide Semiconductor,CMOS)摄像机更加经济可行。高频成像过程可以提供高时相信息,并且利用更多的帧数还可以提供更为充分的轨迹信息。综合考虑以上现有算法在暗弱目标检测效果方面的不足和高频成像的优势,本文借鉴TBD 算法利用轨迹连续性的思想,提出了一种时空域中检测与跟踪相互迭代(Detection and Tracking mutual Iteration,DTI)的算法来对空间中运动的暗弱小目标进行检测。
DTI 运用以时间域信息补充空间信息的思想:使用高频相机捕获运动小目标,可以增加目标在像元处的驻留时间,利用相对较多的帧数可以构建更为准确的时域背景估计[6],累积更多待测目标的能量。这从本质上扩展了先验信息,解决了现有算法无法解决的先验信息不充分导致的目标与背景不可分问题。另外,DTI 在跟踪过程中利用动态规划(DP)算法极大地缩小了搜索空间的尺度,解决了TBD 算法计算量大、不易实现的问题;并且,检测与跟踪的过程迭代进行,可以更加充分地交互利用时空域信息,以达到对LSNR 目标的探测的目的。
1 数据模型定义及预处理
1.1 检测数据模型
包含暗弱小目标的可见光成像图序列f(x,y,k)可以被式(1)描述:
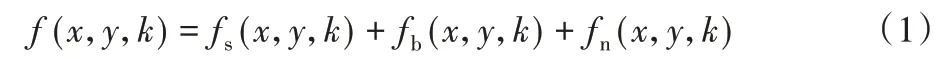
式中:x、y表示成像平面的水平轴和竖直轴;k是视频的帧序号;f、fs、fb和fn分别是观测信号、目标信号、背景信号和噪声,背景fb是一个缓慢变化的二维随机过程。凝视拍摄的模式中背景变化极小,通常占据了整个观测信号f的低频部分。噪声分量fn是传感器电路产生的各类噪声的总和,fn和fb不相关且在空间分布是随机的。
小目标的亮度模式可由光学系统的点扩散效应[16]建立,它的亮度分布遵从点扩散函数(Point Spread Function,PSF)约束。由能量守恒可知光子在像素的分布比例总和为1:

其中h(x,y)是光子在感光器上的分布比例。由光学理论可知,衍射现象中能量的大约84%集中在中央艾里斑,其余能量依次分布在衍射环上。艾里斑强度分布服从1 阶贝塞尔函数[17],强度分布可以由PSF表示:

其中B和b由式(4)计算:

其中:F为焦距,f为光圈大小,x是感光器上成像位置与目标中心的相对距离,J1(bx)为一阶贝塞尔函数。本文用简化的PSF仿真,如式(5):

其中:τ是目标的强度幅值;Δx、Δy分别为目标在x、y方向的扩散宽度。
1.2 基于自适应小波包的去噪
图像预处理可以改善原图的SNR,此步骤可以明显地提高检测算法的检测效率。预处理过程的主要目标是减少杂波信号、抑制背景、增强目标信号,可以选择合适的空域图像预处理方法。本文检测器运行在时序一维信号中,因此本节主要介绍考虑信号的时域特征。本文使用小波包重建的方式对检测数据逐像素地在一维进行去噪,依据目标和背景噪声的小波系数的不同,对噪声的小波系数进行抑制使得SNR 得到提升。
1.2.1 小波包变换的去噪原理
传统频率分析,如傅里叶变换、Z 变换等存在时频信息不完整的问题。利用小波变换[18]可以得到不同频率信息的信号分量在时域的分布情况,它使用一组正交的、迅速衰减的基函数对原信号进行拟合,基函数可通过其尺度变量和平移变量以获得不同的频率和时间位置。
如图1 所示,小波包分解进一步将小波变换没有分解的高频部分D1和DA2子频带空间进行分解,而正是这种多层次的分解提高了时频分辨率。图中信号s可由第1 级分解的系数集A1和D1重建恢复,也可由第2级分解系数集AA2、DA2、AD2、DD2 重建,类似地也可由第3 级分解系数集重建。分解层次越深,某一系数子集与原信号s中某种分量的对应关系越精细。一般而言,噪声信号对应于分解系数高频子带,选择合适策略减小该高频子带系数可抑制原信号s中的噪声。

图1 小波包三层分解结构Fig.1 Three-layer decomposition structure of wavelet packet
1.2.2 自适应小波包去噪
图像序列信号的时域表示,目标经过特定像元时造成瞬态冲击。基于小波包阈值分割的去噪算法的核心点是选择合适的分割阈值,使噪声分量尽量得到抑制而保留冲击目标信号。令式(6)为观测得到的时域一维信号的小波包变换的系数集。

其中:k表示分解层数,j则是该层的第j个系数。根据D可以无失真地重建被分解信号,记Dr为D经过噪声系数抑制的结果,则dr为小波包系数集中的元素。现有的硬阈值和软阈值小波系数分割函数分别为:

其中:thr是手动指定的分割阈值,关于thr的选取,有通用阈值规则、启发式阈值规则和极大极小准则阈值规则等。以上阈值选择策略无法解决thr太大则目标信号被削弱、thr太小则噪声抑制效果不显著的矛盾。
考虑到待测目标的冲击特性,本文根据该特性提出了自适应调整的阈值分割策略,通过计算冲击特性的某个特征值来自适应调整阈值变化,从而达到抑制噪声的小波系数、增强目标的小波系数的目的。鉴于峭度这个统计量对冲激信号十分敏感,所以选择信号的峭度因子作为表征冲击大小的特征值。峭度因子是归一化的四阶中心矩,表达式为:

定义基于Kdj的调整因子:

假设小的都是由于噪声引起的。基于这个假设,高频子带的小波系数应赋予更小的调整因子。给出以峭度因子作为统计特征的自适应阈值分割表达式为:
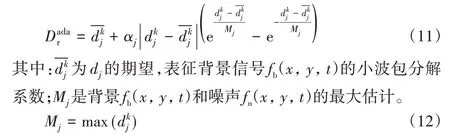
式(11)后面的指数因子是为了减小如软阈值和硬阈值分割中截断效应的影响,使得在固定调整因子αj的情况下,分割曲线的映射更加平滑。图2 给出了本文提出的自适应分割函数(ada thr)和硬阈值分割函数(hard thr)、软阈值分割函数(soft thr)的比较(固定调整因子a=1),更加平滑的阈值分割函数对原信号的小波重建系数畸变更小,因此对原信号中目标信号的成分影响更小,dr指经过阈值分割函数变换后的系数值。
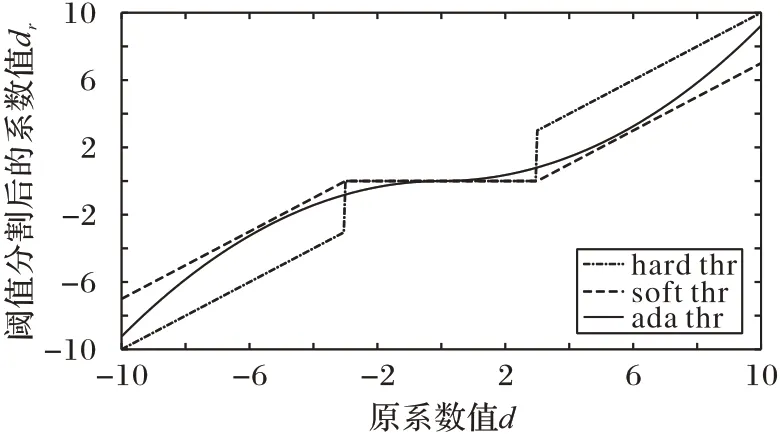
图2 阈值分割函数的对比Fig.2 Comparison of threshold segmentation functions
2 DTI算法
2.1 DTI算法框架
本文假设待检测目标的数据由摄像机凝视拍摄获得。鉴于使用高帧频相机捕获待测目标,可假定目标做匀速直线运动。检测系统整体框架由预处理模块、检测模块和轨迹关联(跟踪)模块组成,后两者在运行过程中互相迭代进行。可以抽象地用D和T分别标记检测与跟踪模块,用A标记检测器参数。记第n阶段的检测结果和跟踪结果分别为Dn、Tn,且检测器参数集合为An,则这三者在整个算法运行过程的依赖关系可以由式(13)解释:

式(13)表明现阶段的跟踪结果由此阶段的检测器输出决定。后一阶段检测结果由被检测器参数An+1决定,而An+1是由前一阶段的跟踪结果Tn决定的。
本文算法中检测与跟踪过程迭代,时空域信息交互利用,最后输出迭代最优。检测输出作为跟踪模块的输入,跟踪模块进行轨迹关联并自适应调整轨迹处的检测器参数。通过设置一个衰减因子来根据第n轮轨迹关联的结果调整第n+1 轮检测器参数An+1中的判决门限。调整策略是在第n+1 轮检测中令检测器倾向于把疑似目标轨迹延伸处的信号片段判定为目标信号经过的片段。而疑似目标轨迹的延长(轨迹的能量累积),又使得该轨迹自己在下一轮轨迹的筛选中被保留下来的可能性增大。
根据轨迹关联的结果判断所有候选轨迹的真实性,若判断该轨迹是由伪目标造成,则需重新初始化检测窗口的参数,直到该参数超出预设的范围值,而该范围的边界则与对真实目标的运动速度有关。图3给出了本文算法流程的整个框架。

图3 DTI算法框架Fig.3 DTI algorithm framework
DTI算法运行流程:
1)输入:多帧图像f(x,y,k);
2)从i=1,2,…,k对每帧f(x,y,i)预处理;
3)从i=1,2,…,x,从j=1,2,…,y对每个像素点f(i,j,k)进行小波包去噪;
4)初始化或者重置检测器的参数集A;
5)从i=1,2,…,k根据A检测图像数据f(x,y,i)得到检测标记数据;
6)对检测标记数据进行霍夫线检测得到待选轨迹,将这些轨迹保存在表格中;
7)对表格中各条轨迹的能量进行累积计算,并根据能量计算值大小动态地调整检测器分割阈值Th;
8)转至步骤5),直到表格中的条目为1;
9)如果轨迹判断为真,则输出结果,如果A超出范围,则DTI算法退出;如果不满足上面两条,则转至步骤4)。
2.2 检测模块
检测模块中,检测算子计算窗口内当前信号片段与背景的差别时使用核函数构建。本节简单介绍核函数的基本原理和基于核函数的检测模块。
2.2.1 核函数原理
数据在低维空间中线性不可分时,可以用增加特征维度的方法在高维空间中寻找超平面划分这些数据。利用核函数[19-20]则直接在输入空间中计算映射到高维特征空间H(Hilbert空间)中的两个数据的内积。

其中,Φ:x∈χ→Φ(x) ∈H为从输入空间到特征空间的映射函数。
2.2.2 基于核函数的时域检测架构
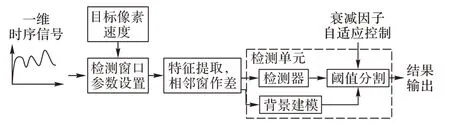
图4 DTI的检测器Fig.4 Detector of DTI
运用假设检验的思想构建各像素采集点一维时域信号的检测器,然后将检测器逐像素地由空域顺序遍历全部像素点以完成一个阶段的检测过程。
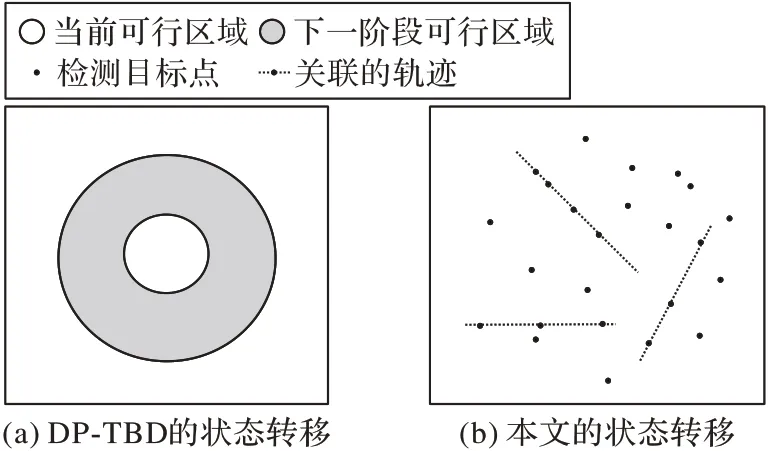
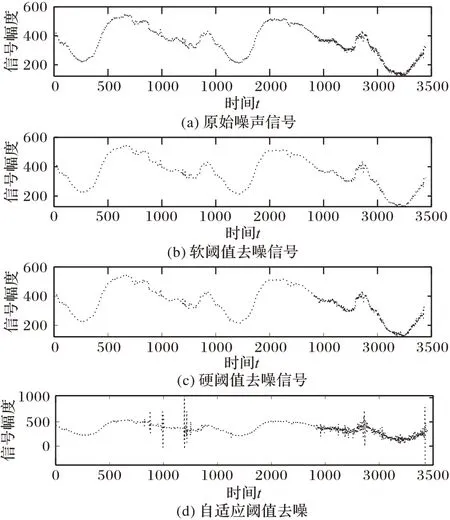
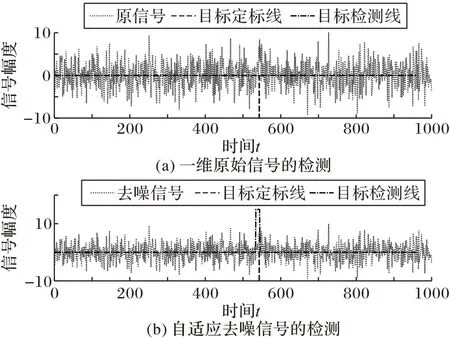
如图5 所示,对信号Fxy(t)设置了长度为l的检测窗口,检测窗口的特征统计记为fl(x),则该窗口的直接后继窗口为fl(x+d)(需要注意的是,这里的x是指某一像素点时间维t上的某个位置,不是该像素空间域的横轴坐标),其中,l表示窗口长度,x为窗口的起始坐标,d(0 图5 中让信号延迟d和窗口长度l相等,两个检测窗口的特征统计关联为式(5),表示相邻两个信号片段的统计变化量: 图5 时域一维信号的检测Fig.5 Detection of one-dimensional signal in time domain 为了方便描述,可将式(15)简洁为式(16): 由希尔伯特核空间理论可知,fl(x,x+d)可以构造为核函数形式。由于暗弱小目标的SNR 极低,目标信号和背景噪声在幅度上线性不可分,假设检验中简单的阈值分割无法准确判别信号和背景,所以利用核技巧以达到在高维空间中解决线性不可分的目的。令y=x+d,给出单像素的特征统计表达式由高斯核函数的形式所定义: 式(17)也可以被认为是坐标分别为x,y处的一种广义距离度量。则在窗口长度l上的归一化统计量为: 至此,知道了两个检测窗口可以获得一个关联的特征统计值ki(i=1,2,…,n): 这里假设相机拍摄了n帧图像,i表示第i个统计特征值。将两个检测窗口同时在时域向t:1 →end 的方向滑动一个时域坐标直至最后一帧可以获得一个n维的特征向量K={k1,k2,…,kn},则该像素背景的统计特征模型定义为K的期望,如式(20)。 此检测算法运行在时域,逐像素地进行检测。将所有视频帧的同一像素点的时序信号看成一维信号f(t),把检测目标是否经过、何时经过该感光像素的模型简化为检测一维信号中未知出现位置、未知长度的信号检测问题。把这个一维信号检测问题作为一个假设检验问题,记有像素区域内不存在目标(H0)和存在目标(H1)这两种假设: 式(22)是对式(1)在时域一维的抽象表示,f(t)、x(t)、b(t)和n(t)分别表示时域中的观测信号、目标信号、背景信号和噪声信号。利用凝视拍摄模式中背景恒定和噪声的分布在短时间内变化不大的特性,检测目标是否存在。当有目标经过时则会造成冲击,改变原有的信号分布,使得式(23)成立: 其中:Kt表示一种广义的信号特征提取机制,本文中可以用特征向量K实现;t1和t2是不同的两个相邻时刻,不等号左侧用Kt提取观测信号在这两个时刻用一阶差分形式关联的统计特征。在不存在目标的情况下,一般来说各个时刻提取的统计值变化不大。当出现目标信号时必然使得式(23)不等号成立。DTI 检测器利用目标会改变Kt提取的特征值的特性进行判断检测。在一定置信度准则下有式(24)~(25)成立: 其中:B表示对该像素一维时域信号的背景估计,可以用各检测窗口核空间相关性的期望计算,即式(20)。换句话说,在式(23)中,用Kt提取所有时刻关联的特征值并进行平均就是B的估计值。ΔB是特征向量K的方差估计: Th是可预设初始值的分割阈值,较大的Th提高检测率,但也会增加虚警率。注意,Th值是基于跟踪模块轨迹关联与筛选结果在不同像素上自适应调整的参数。 检测窗口参数设置:假设待测目标的直径为R,与摄像机距离为D,运动速度为V,且摄像机焦距为f。根据相机的光学成像原理,可得目标像素直径和像素速度分别为: 令该摄像机的采集帧频为pHz,则目标信号在时域的持续时长为: 窗口尺寸严重依赖于目标在时域信号的持续时长,如果二者不匹配则会极大降低信号对背景的有效区分性,故该检测系统需要目标大致的运动速度和尺寸的范围作为先验条件。 检测模块算法流程 首先,初始化检测参数;然后,用核函数提取每个检测窗口的特征,在时域上滑动窗口,得到背景特征的估计;最后,将每个检测窗口提取的特征与背景估计做阈值分割,得到检测结果。 2.3.1 基于动态规划的跟踪原理 基于动态规划[12]的跟踪策略依赖于: 1)沿着目标轨迹能量累积最大。 2)只需要令剩下轨迹能量最大的最优决策可以使得整个目标轨迹的能量最大化,而不用考虑过去的状态和决策。 令Ti表示第i帧中目标的坐标[x,y],定义目标的轨迹能量为: 其中E(Ti)可以用该坐标处像元亮度表征。轨迹的能量依赖于轨迹的长度和轨迹内各坐标点的像元亮度。式(30)将一个多阶联合决策过程弱化为多个一阶决策过程。DP 将联合过程分段化,有助于解决穷举搜索整个决策空间而造成的计算量大的问题。穷举搜索M×M×N的待测数据,计算量正比于M2N,而使用动态规划解决这个问题计算量与M2N成正比。 状态转移是动态规划算法里的关键环节,也决定了动态规划算法的优劣。DTI 状态转移指将第n轮跟踪过程中轨迹关联的结果作为第n+1 轮检测的输入,第n+1 轮检测器的输出即是第n轮检测的下一状态。所以从动态规划的角度可以定义检测过程D、跟踪过程T和参数更新规则A为状态转移方程。综合式(13),有: 基于DP-TBD 算法的目标可能出现的区域(状态转移的可达状态)一般以目标的当前坐标为中心、由目标运动速度等其他因素影响形成的环形区域。图6 展示了DTI 状态转移和DP-TBD 状态转移的差异,图中DTI的状态转移由关联的轨迹的更迭表示。 图6 动态规划的状态转移区域Fig.6 State transition region in dynamic programming 2.3.2 跟踪过程的轨迹关联准则 利用霍夫直线检测算法检测所有疑似目标的轨迹。将这些轨迹以能量从高到低的顺序排列,并将这些信息以索引表的形式储存起来。 由图7 所示,以轨迹的能量高低进行排序。根据被保留轨迹的起止点得到该轨迹的三维空间表达式。下一轮检测过程中只检测被保留轨迹覆盖的像素。所有待检测像素的分割标记值和特征向量Ki在第1 次做检测时已经被计算过,所以后续阶段的检测过程不需要重新计算。故只需将检测器参数A根据轨迹关联结果更新,本文采用衰减检测器的判决阈值Th的策略: 图7 轨迹关联中的轨迹筛选Fig.7 Trajectory selection in track association 其中:Th,n是指第n轮检测过程中某个轨迹所覆盖的所有坐标处的局域检测分割阈值。衰减因子α调节每条轨迹、每轮跟踪过程中轨迹覆盖点坐标的通过率。 对于检测阈值Th,每个轨迹以及每个轨迹的每个检测阶段都有不同的取值。后续迭代只需再做一次简单的阈值分割。显然,相较于第1 次粗检测,后续检测过程的计算量被极大地减少了。 实际拍摄数据中由于LSNR 的原因,即使霍夫线检测器中,能量累积最高的坐标点(霍夫变换空间中点对应原像平面中一条线)对应的轨迹中也有很多检测缺失点。本文的核心理念是利用检测与跟踪过程相互迭代,交互利用空间域和时间域的信息得到可信度较高的目标轨迹。重复检测与跟踪过程直到将表格里的轨迹数量消除到只剩一条。最后判断这条轨迹的真实性:若得到的轨迹不可信,则在提供的目标速度和尺寸范围内更新检测窗口尺度,直到以一定步长遍历整个区间;若最后还是没找到可信任轨迹,则该检测算法宣布无目标。 3.1.1 一维信号的检测 由于算法的检测器工作在像素的时域信号中,需要验证去噪算法和检测算法在一维信号中的检测性能。在噪声模式为高斯白噪声、目标信号为时域高斯钟形信号的仿真条件下,图8 展示了自适应小波包去噪算法的SNR 增益。可以看出,对于SNR 为0 dB 及以下的含噪声信号,经过去噪后SNR 可以提升大约4~6 dB。 图8 自适应小波包去噪的SNR增益Fig.8 SNR gain of adaptive wavelet packet denoising 图9 是在Matlab 信号处理工具箱内置样例信号leleccum上的表现,可以看出软阈值和硬阈值分割算法虽然可以消除高频噪声,但对冲击信号没有增强作用。自适应去噪算法对冲击分量有极大的增强效果,在1 000、1 200 处冲击被增强。实际应用中需先对信号做平滑处理,再使用该去噪算法。 图9 leleccum信号上不同小波阈值去噪算法的效果对比Fig.9 Effect comparison of different wavelet threshold denoising algorithms on leleccum signal 模拟生成SNR为0的一维信号st,经过基于小波包重建的自适应去噪算法获得SNR 为4.95 dB 的信号,可由检测器定位持续时长极短的目标信号片段。如图10所示,对于0 dB左右的一维时域信号,检测器能以较高的检测率正确定位目标的位置。目标SNR 极低,无法直接在原信号中发现位置,图10 用一根竖直的定位虚线在仿真的目标下面作位置标记,用水平的粗线标记检测结果,矩形框标注目标所在的位置。可以看到未经去噪的信号没有检测到目标。 图10 一维信号的去噪与检测Fig.10 Denoising and detecting for one-dimensional signal 3.1.2 仿真数据的检测 仿真生成1 000 帧100×100 的图像构成视频,该视频中包含了一个从像平面左上角向右下角做匀速直线运动的点目标。该目标占1 pixel,其SNR 为0 dB,像素速度为0.1 pixel/s。图11是从上述方法中生成的图像序列中截取的一帧图像。 图11 0 dB SNR仿真视频的X-Y投影图Fig.11 X-Y projection of simulation video under SNR of 0 dB 图12 为在其他参数不变,SNR 分别是0 dB、1 dB 和3 dB的情况下对仿真目标做检测与轨迹跟踪的展示。对仿真视频(三维数据)做检测得到同尺寸的判别数据,将判别数据在时间维度进行投影获得像平面的空间轨迹如图12 所示。可以发现,在0 dB 的LSNR 下,DTI 算法依旧可以检测到明显的轨迹轮廓;随着SNR 的提升,对暗弱目标轨迹的检测率会进一步提升,人眼观察到的轨迹也更加明显了。 图12 三种SNR下对仿真数据的检测结果Fig.12 Detection results of simulation data with three SNRs DTI 算法与其他算法的比较结果如表1 所示。表1 中,Top-Hat[7]是一种只对图像单帧进行形态学变换检测目标的算法。背景差分[6]是利用连续少数几帧图像做图像检测的算法。这两种算法设计简单,结果非常不理想。与基于高阶谱分析的高阶统计量算法[12]、基于动态规划的DP-TBD[14]和三维匹配滤波[11]等算法相比,本文算法DTI 能在较低虚警率的前提下以高检测率检测到目标。 表1 0 dB SNR下不同算法检测结果对比 单位:%Tab.1 Detection result comparison of different algorithms under SNR of 0 dB unit:% 为了验证DTI 算法对实际暗弱小目标的检测与跟踪能力,在实验室的暗室中拍摄小球作为待检目标进行实测数据的验证实验。实验设置在完全控制光照亮度的暗室中,拍摄自由降落的小物体,物体直径为15 mm,拍摄距离为14.50 m。通过以上措施模拟LSNR 的天基空间环境。本实验使用75 mm的长焦镜头和德国Mikrotron公司生产的一款高帧频工业摄像机EoSens®Cube7 以1 000 fps(frames/s)进行拍摄,用获得的480×480×3 000 的视频数据测试DTI 对真实数据的检测性能。 图13(a)为实拍数据的某帧截图,添加的矩形框标示目标轨迹的区域。图13(b)为截取矩形框位置的5 帧图像拼接而成,为了目标的显示清晰,对目标做了显化处理。图14(c)为对目标检测与跟踪后投影到二维的轨迹。可以发现,对于此LSNR 的小球目标,DTI 算法可以检测到目标的运动轨迹;但是LSNR 下,轨迹中会有大量的缺失点,并且这种情况会在SNR小于0的条件下逐渐加剧。 图13 实拍小球的检测Fig.13 Detecting for real captured small ball 本文针对LSNR 暗弱小目标检测提出了一种新的算法,该算法改进现有的TBD 算法,将检测与跟踪过程联合、迭代以提高检测能力。经过仿真和实际数据的验证分析验证了DTI 算法的有效性。与TBD 算法相比较,在检测率和虚警率上DTI算法的表现更优。 不过DTI 算法检测窗口的长度依赖于待检测目标的速度、尺度和距离等运动参数。这些先验信息是LSNR 目标所不能提供的,因此本文采用首先估计待检测目标运动参数的大致范围,然后再滑动搜索该范围的算法。为了避免算法运行之前人为指定运动参数偏差,所以接下来的工作是进一步解决自适应估计此参数的问题。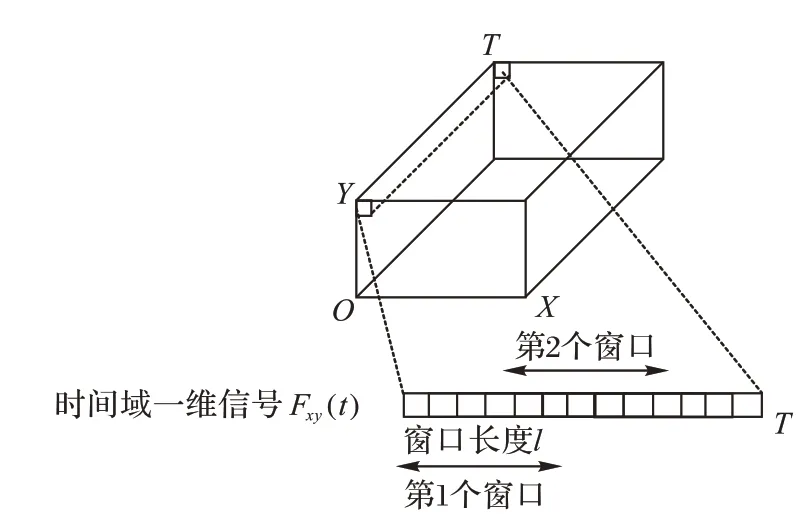

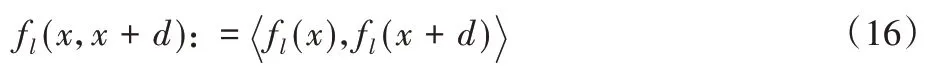




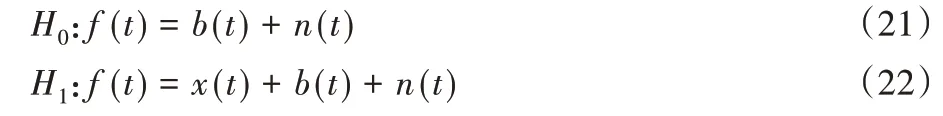





2.3 跟踪模块
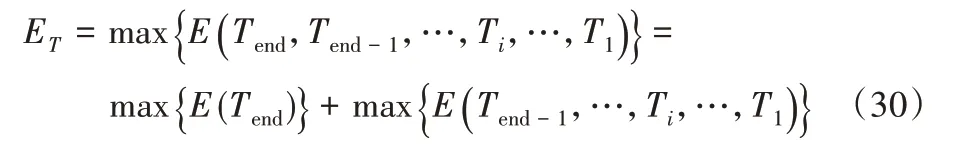




3 实验仿真与结果分析
3.1 仿真数据分析




3.2 真实数据验证

4 结语

