点格棋计算机博弈系统的设计与实现

倪锦园 张建勋

DOI：10.19850/j.cnki.2096-4706.2021.09.021

摘  要：计算机博弈是当前人工智能领域的主要研究方向。在点格棋计算机博弈的过程中，搜索引擎在开局阶段会花费大量的时间，搜索出来的节点不够优秀，由此造成整体棋力不够强。为了解决此问题，该文设计了一种结合开局库策略的MiniMax算法，并将此算法作为整颗博弈树的搜索引擎，以强化计算机的算力，提高程序的整体效率。实验结果表明，该文提出的搜索引擎具有更高的准确率和更好的鲁棒性。

关键词：计算机博弈;蒙特卡洛;开局库;MiniMax

中图分类号：TP311.5 文獻标识码：A 文章编号：2096-4706（2021）09-0078-05

Design and Implementation of Dots and Boxes Computer Gaming System

NI Jinyuan，ZHANG Jianxun

（School of Computer Science and Engineering，Chongqing University of Technology，Chongqing  400054，China）

Abstract：Computer gaming is the main research direction in the field of artificial intelligence at present. In the process of dots and boxes computer gaming，the search engine will spend a lot of time in the opening stage，and the searched nodes are not good enough，resulting in the overall chess power is not strong enough. In order to solve this problem，this paper designs a MiniMax algorithm combined with opening library strategies，and uses this algorithm as the search engine of the whole gaming tree，so as to strengthen the computing power of the computer and improve the overall efficiency of the program. Experimental results show that the proposed search engine in this paper has higher accuracy and better robustness.

Keywords：computer gaming;Monte Carlo;opening library;MiniMax

0  引  言

计算机博弈是一个充满着智慧和无限挑战的科学领域^[1-3]，它主要研究的是让机器模拟人类思考的过程，并通过更加强大的计算能力来获得更好的运算结果。笔者曾参加全国大学生计算机博弈大赛，独立设计并开发了点格棋计算机博弈系统，并于比赛中取得二等奖的成绩。在计算机博弈领域中，点格棋属于零和完全信息博弈^[4]，由11×11大小的棋盘组成。对于计算机的搜索计算量，这个数据量非常庞大，构造一颗完整的博弈树，则需要1111数量级的空间大小，这对计算机的空间要求是十分高的。因此在点格棋博弈项目上探索一种好的搜索引擎是非常困难的。目前对于点格棋博弈研究主要用蒙特卡洛算法配合估值函数作为搜索引擎，但由于在前中期搜索节点会花费大量的时间，且搜索出来的节点不是很好，导致点格棋的棋力难以得到较大提升^[5-7]。

针对以上问题，该文设计了一种结合开局库策略的MiniMax算法作为搜索引擎，通过不同的开局库策略让己方棋子在博弈开局阶段处于优势地位，在中期阶段通过MiniMax算法和经验搜索布局来进行落子，在博弈双方进入终局阶段后，如果双方的棋局进入我方终局必赢策略，此时程序将直接调用终局库，胜率会达到100%。

1  点格棋计算机博弈规则

点格棋计算机博弈系统的规则是根据全国大学生计算机博弈大赛的规则制定的，详细的规则为：

（1）双方轮流将两个相邻的点连接成一条边，不可以超越两个临近点，不可以填充重复的边，不可以连接一个格子的对角线。

（2）边属于双方共有，只讨论格子的所属。

（3）当某一个格子的四条边都被连成线时，占领最后一条边的玩家拥有这个格子。

（4）占领格子后有一个奖励边，该玩家必须再下一步。

（5）格子全部围成后，博弈结束，占领格子较多的一方为获胜方。

一个11×11点格棋棋盘如图1所示。

2  算法介绍

2.1  MiniMax算法设计

对于很多十分复杂的棋局，有一个好的搜索算法和一个完善的估值函数可以很大程度上搜索到当前局面的最佳走步。MiniMax算法就是一种可以找出最优解的算法，属于零和博弈的一种。目的是让己方以优势最大的方式去落子，让对方以优势最小的方式去落子，其总和为0，如同此消彼长的能量守恒。更进一步解释，博弈树的层次也分为奇偶层，对于落子的一方来说，其中的最优走步就是在他下一层节点的最优来选择，如果这个估值的选择上我方可以得到最大的收益的话，这个搜索就为“Max搜索”，同时这个估值对于对方来说是最小收益的话，这个搜索就是“Min搜索”^[8]。

对于不同局面时，都能够以当前局面作为根节点，然后以该根节点建立一颗深度固定的博弈搜索树，博弈树出度为0的位置作为叶子节点，叶子节点的位置也就是当前落子的位置，但由于计算机内存硬件有限，在博弈前中期搜索过程中很难搜索到叶子节点，一般通过人为设置每步落子的搜索时间或者博弈树迭代深度来控制落子。

极大极小算法的伪代码示例程序为：

01 maxmin（player， cur_node）

02     if depth = 0 or node is a terminal node

03         return the heuristic value of nod

04     if maxPlayer

05         bestValue ：= -∞

06         for each child of node

07             v ：= minimax（child， depth - 1， FALSE）

08             bestValue ：= max（bestValue， v）

09         return bestValue

10     else miniPlayer

11         bestValue ：= +∞

12         for each child of node

13             v ：= minimax（child， depth - 1， TRUE）

14             bestValue ：= min（bestValue， v）

15         return bestValue

在棋盘大小为11×11的点格棋博弈过程中，由于需要1111数量级的空间大小，一般计算机难以达到这个量级的搜索量，所以通过限制搜索层数或者限制搜索时间，利用MiniMax算法搜索得出最佳的落子，因此无论是时间上还是空间上，此方法都是可行的。

2.2  MiniMax类设计

该文设计的MiniMax类如表1所示。

MiniMax类中的部分属性如表2所示。

MiniMax类中的部分方法如表3所示。

2.3  MiniMax搜索流程图

整颗博弈树通过MiniMax配合估值函数进行搜索，MiniMax算法是一种找到对己方最有利的走步，同时也是对对方最不利的走步。MiniMax搜索算法主要是用递归实现的，递归是程序里面一个重要的思考策略^[9，10]，通过深度优先模拟出更深层次的节点。MiniMax算法是在双方博弈过程中，尽量让己方的优势最大，让对方优势最小，其输赢的总和为0。

该文提出的MiniMax搜索步骤主要分为：初始搜索树、是否为叶子节点，是否时间结束，递归搜索等。MiniMax搜索流程图如图2所示。

MiniMax搜索主要通过以下三个步骤：

（1）初始搜索树，首先在一颗空树上创建根节点，然后在其子节点上创建可以走步的节点，接下来可以设置每一步搜索模拟时间，目的是为了防止比赛时间超时，然后用一个变量保持棋盘的信息，后面的模拟过程全部都在这个变量上进行演练。

（2）是否为叶子节点，初始化树后会直接进入递归搜索的阶段，进入递归搜索模拟之前会判断该节点是否是叶子节点，如果是叶子节点会直接返回叶子节点，如果不是叶子节点会进入下一步判断。

（3）时间是否结束，進入循环模拟时，会一直递归向下搜索节点，直到搜索到一个最佳节点为止，但由于时间限制，大部分情况是搜索不到叶子节点的，会在时间结束时返回一个当前的节点。

3  开局库策略

一个好的开局往往是赢得比赛的基础，在开局阶段通过设计开局库来节约前期搜索节点的时间，同时也可以让局面在前期保持一定的优势，因此需要一个良好的开局库来让程序在整个对局中处于强势地位。要设计一个良好的开局库需要通过大量的测试并且通过观察高手之间的对局情况，然后经过不断地模拟，抽象出一套自己系统可以使用的开局库。

基本上所有优秀的棋类博弈系统都有自己特殊的开局库，如果不采用开局库，而在开局阶段就直接通过MiniMax搜索出的走步，这样有可能会出现一些很不好的落子，所有我们需要在开局的时候加入一些经验算法规划，这是十分关键的。如果使用了开局库，在前期可以通过对手的情况来改变自己的本局的开局策略，可以避免对手进行针对性落子，总体来说开局库模块对于整个系统来说，都是必不可少的一环。

3.1  常规开局库策略

开局库就是把一些基于经验的固定走步存在数据库里，然后在开局阶段从数据库中调用这些数据从而在开局阶段拥有好的收益。常规开局库图如图3所示，在该文常规开局库的设定是先占领图内置的边，再通过占领外置边达到开局库的作用，由于博弈双方下的边是共有的，所以在落子后并未在交互界面用不同颜色加以区分。

3.2  镜像开局库策略

镜像开局策略可以模拟对方的落子情况，通过镜像的方式，重现对方的开局，当面对实力比较强的对手时，通过该策略避免在前中期开局不利的情况，也可以学习对方的开局从而增加自己的开局库信息。镜像开局效果图如图4所示，在前22步都启动镜像开局策略来模拟对方开局。

4  搜索引擎架构

整个搜索模块是点格棋博弈系统最核心的部分，是决定整个系统棋力强弱与否最关键的环节。其中一些主要功能为：

（1）判断落子功能：在这个模块里，程序可以自动识别玩家或者电脑落子是否规范，并且可以判断整个游戏是否结束。

（2）搜索节点功能：整个搜索模块主要是寻找最佳走步，在建立的博弈树上进行搜索，只有具备完善的搜索节点功能，整个系统的棋力才能得到质的提升。而在开局阶段主要采用开局库策略和经验算法策略进行搜索得出最优点，后期采用极大极小值算法策略得到最佳落子节点。

（3）信息保存功能：在程序下棋的过程中会把每一步的信息按打谱软件格式全部记录下来，方便以后的测试和修改。

（4）搜索时间功能：由于比赛时限的原因，可以限制每次落子的搜索时间来保证整局游戏不超过比赛的总时长。

在点格棋博弈系统整体架构中，把整个棋局分为前中后三个阶段。首先在开局时，使用上一小节提到的开局库搜索，在此阶段，主要是以开局库经验策略为主，在中盘阶段，优先调用依赖经验设计的函数构建布局，然后通过MiniMax算法搜索落子，最后是终局阶段，进入这个阶段说明游戏即将结束，如果在终局阶段进入终局库里面，系统会自动调用终局必赢算法，此时胜率将达到100%。

在开始阶段通过电脑落子可以判断开局库的使用是否成功，大概在22步之前都使用开局库策略，然后通过MiniMax算法搜索，得出最佳节点。搜索引擎流程图如图5所示。

5  实验结果和分析

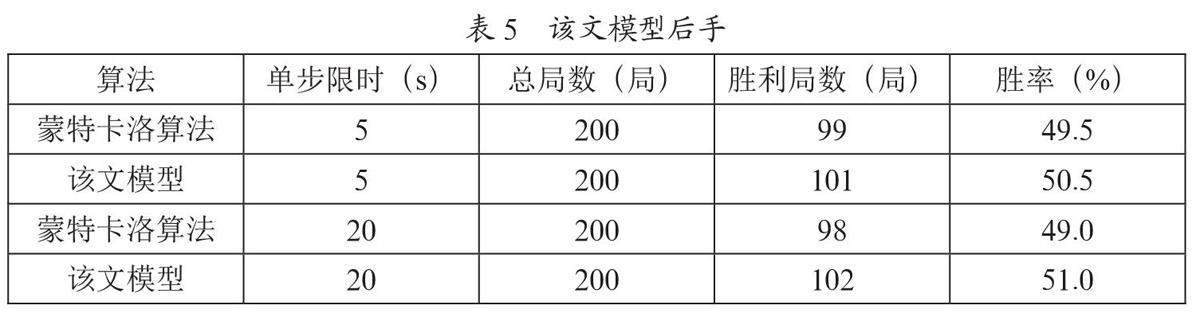
为了验证该文提出的结合开局库策略的MiniMax算法有效性，将该策略与蒙特卡洛算法进行博弈对局测试，棋盘大小11×11，单方用时不超过15分钟。该实验环境包括：GPU型号为NVIDIA GeForce RTX 2060（6 GB），CPU型号为Intel Core i7-10700F。如表4、表5、表6所示。

由表4、表5、表6可以得出，该文提出的模型在先手时的胜率明显更高，虽然在后手时胜率难以得到保证，但仍然在50%以上，随着单步限时的增长，该文提出的模型胜率也更高。

6  结  论

在如今快速发展的人工智能领域中，计算机博弈研究是十分值得的。计算机博弈过程中节点的搜索都是在博弈树上进行的，几乎都是通过深度优先算法同时加上估值函数来对整个局面进行判断，然后进行评估落子，其中常用的就是MiniMax算法、UCT算法等。未来改进该系统时可以加入置换表，把训练搜索到的节点情况存入哈希表中，这样在博弈比赛时遇到类似的搜索情况，便可直接调用哈希表中的值来节约搜索时间。

参考文献：

[1] 吕征宇.基于深度强化学习的棋类博弈研究 [D].北京：中央民族大学，2020.

[2] 姬波，尤惠彬，卢红星，等.一种自对弈棋局学习样例质量评价方法 [J].小型微型计算机系统，2021，42（3）：467-471.

[3] 刘成，李飞，孙玉霞，等.贯穿式案例教学法在机器博弈课程中的实践 [J].计算机教育，2019（8）：174-178.

[4] 闫俊名.双人零和博弈问题中策略搜索算法的研究 [D].大连：大连理工大学，2020.

[5] 王允臣.基于点格棋的博弈算法研究与改进 [D].徐州：中国矿业大学，2017.

[6] 張利群，曹杨，李厦.点格棋计算机博弈平台通信接口 [J].计算机与现代化，2016（3）：96-99+126.

[7] 丁濛，张亦鹏，李淑琴.棋盘局面数据标定方法研究 [J].计算机应用研究，2020，37（2）：470-472.

[8] 申培萍，陈晓.一类Minimax分式规划问题的迭代算法 [J].河南师范大学学报（自然科学版），2018，46（1）：16-22+2.

[9] 倪锦园，张建勋.递归算法的应用与分析 [J].现代信息科技，2020，4（20）：146-148+152.

[10] 杨娇.递归思想及其算法设计的探讨 [J].数字通信世界，2018（11）：109+204.

作者简介：倪锦园（1996—），男，汉族，重庆九龙坡人，硕士在读，研究方向：数字图像处理与分析;张建勋（1971—）男，汉族，四川乐山人，教授，硕士生导师，CCF会员，博士，研究方向：数字图像处理与分析、实时计算机图形学。

收稿日期：2021-04-06

基金项目：重庆市教委科技研究重点项目（KJZD-K201801901）