维修人员与维修设备需求的蒙特卡洛仿真研究
吕升全+郭金茂
摘要: 针对装备维修中维修人员和维修设备编配数量这一难题,文章中采用蒙特卡洛仿真法对装备维修进行仿真。提出以维修人员和维修设备满足维修需求的概率以及数量变化的敏感性作为约束,以此确定维修人员和维修设备数量。该方法考虑了维修人员和维修设备之间的相互作用关系,计算结果更加准确。
Abstract: Aiming at the problem of the number deployment of maintenance personnel and maintenance equipment in the equipment maintenance, the article uses Monte Carlo simulation method to simulate the equipment maintenance, proposes to take the probability of maintenance personnel and maintenance equipment to meet the needs of the maintenance and the sensitivity of quantitative changes as a constraint to determine the number of maintenance personnel and maintenance equipment. The method takes into account the interaction between maintenance personnel and maintenance equipment, and the calculation result is more accurate.
关键词: 维修人员;维修设备;需求;蒙特卡洛
Key words: maintenance personnel;maintenance equipment;demand;Monte Carlo
中图分类号:[TJ07] 文献标识码:A 文章编号:1006-4311(2017)36-0180-03
0 引言
装备维修的维修人员、维修设备的计算是一项复杂的系统工程。以往的计算大都按照工时法进行计算[1],或者采用遗传算法[2]、粒子群算法[3]、排队论[4]等理论进行单点的计算,不适宜系统计算。因为维修保障系统是离散动态系统,考虑的因素(维数)较多,采用数学的方程难以完整、准确描述[5]。蒙特卡洛(Monte Carlo)仿真仿真方法的计算复杂性不再依赖于维数,也不需要问题的解析表达形式,因此采用蒙特卡洛仿真法用于求解装备维修人员人员和维修设备数量可以考虑因素更全面,计算更简单。
1 蒙特卡洛仿真步骤
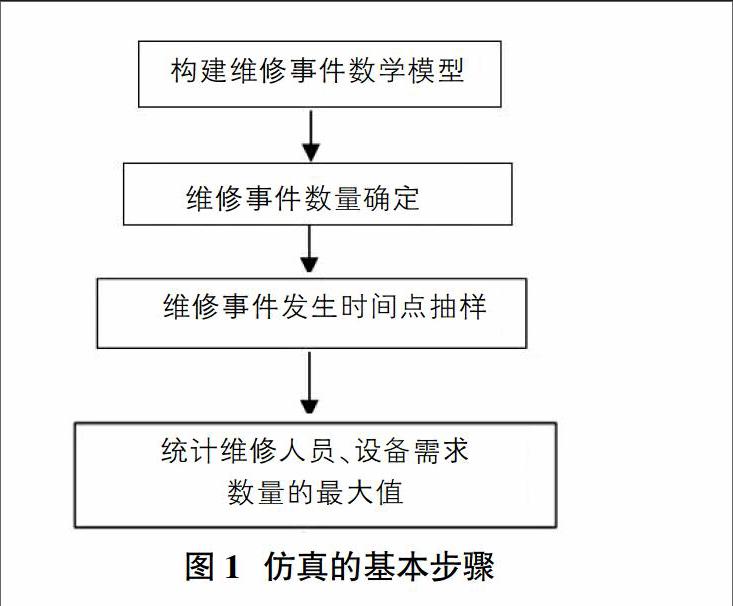
蒙特卡洛仿真的基本思想是:为了求解数学、物理、工程技术等方面的问题,首先建立一个解等于随机过程的参数或数字特征概率模型,然后对模型及进行观察或抽样试验,然后计算这些参数或数字特征,最后给出问题解的近似值。解的精确度用估计值的标准误差来表示[6]。将蒙特卡洛法应用于求解装备维修人员和维修设备数量需求有以下4个步骤,如图1所示。
①确定仿真中的各种离散的维修事件,把维修事件所需的维修人员和维修设备以及维修过程用数学模型表示。
②确定仿真时间内维修事件发生次数,即确定维修工作量的大小。
③将仿真的总时间离散化成一系列时间点,根据维修事件的发生随机分布特点,在仿真时间段内抽取相应的发生时间点。
④统计各个时间点的维修人员和维修设备的消耗数量,并求出最大值。进行多次仿真,统计每次仿真中需求的最大值的分布情况。
2 蒙特卡洛仿真的过程
装备维修事件包括预防性维修和随机故障后的检修。计算维修人员和维修设备的数量主要就是统计所有维修事件中消耗的维修人员和维修设备数量。
2.1 维修事件数学模型的构建
蒙特卡洛仿真中要根据一定概率在计算机上进行抽样,但计算机只能识别数字,因此需要将维修事件涉及到的维修过程、维修人员、维修设备转化成便于统计的数学模型。
维修人员、维修设备数量均可以直接统计数量。而维修过程与时间有关,为了便于统计可以将时间进行分割成一系列时间点。只要时间分割的足够细那么可接近于连续状态。一般维修事件的统计以小时为单位,仿真一般以年作为单位,若取10分钟作为一个计时单位,维修事件的数学模型如下形式:
u=■
该维修事件共5行6列,每一行代表一种维修人员或设备各个时间点(10分钟为一个点)所需数量,6列表示该维修事件需要6个10分钟。
2.2 检修事件的抽样
故障检修的发生有特定的概率分布,常见的概率分布有均匀分布、正态分布、威布尔分布、指数分布等,这些故障的分布表征了单台装备在不同寿命阶段故障可能性的大小。但装备的使用一般是有计划的,处在各个状态的装备是较为均匀的分布,不论某种故障属于任何分布,只要装备数量达到一定程度,对装备群来说故障发生是趋于均匀发生的。
检修事件的抽样即将仿真时间离散化成为一系列时间点,时间点用正整数表示,均匀的随机抽取其中的n个正整数,这n个正整数代表故障发生的时间点。均匀分布的随机数抽样可以由MATLAB软件的R=randi([imin,imax],m,n)函数产生。此函数可以产生m行n列在[imin,imax]区间内的随机整数。imin为仿真的开始时间(一般为0),imax为仿真的结束时间,假设时间的离散化以10分钟作为一个时间单位,其计算公式如下:
imax=144·d=864·h
式中:d——仿真的天數;h——仿真的小时数。endprint
2.3 预防性维修事件的抽样
预防性维修是在故障发生前,使装备保持规定技术状态所进行的维修活动。预防性维修是有计划进行的,以避免出现集中,使得无装备可用,维修任务难以按时完成。因此仿真中预防性维修事件抽样根据实际的维修计划进行,或是设定一个期望值。
3 仿真实例
为了验证方法可行性,本文对某装备维修机构的维修进行仿真。该维修机构主要进行装备的预防性小修和故障的检修。仿真中主要对两种装备的机械专业维修人员和维修设备进行仿真。机械维修专业的维修人员分为高级和普通两种,维修设备主要仿真两种重要的维修设备。
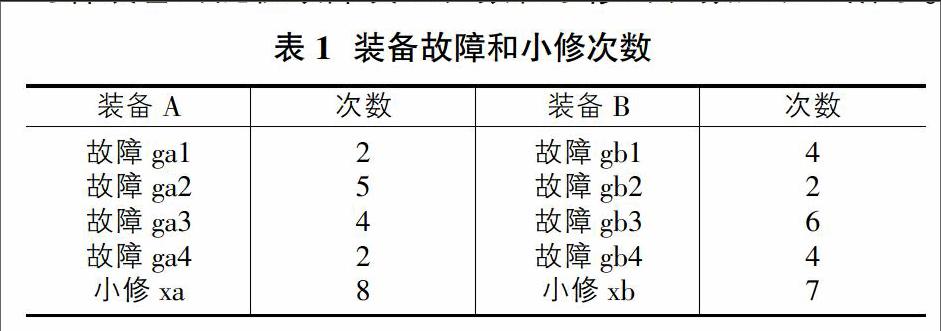
仿真时间周期为1年,一年工作时间为250天,每天工作8个小时,以10分钟为一个时间单位,那么一年共有12000时间点,维修事件发生的时间点在[0,12000]之间。这两种装备的随机故障发生次数和小修的次数如表1所示。
为明确仿真的边界条件,对仿真的条件作如下假设:
①维修是在固定的维修点进行维修。
②每种检修的处理流程均已确定。
③装备群故障的发生是均匀分布。
④装备的小修按计划均匀的进行小修。
⑤小修、检修都能在规定的时间内完成维修,没有返修情况。
3.1 仿真的结果
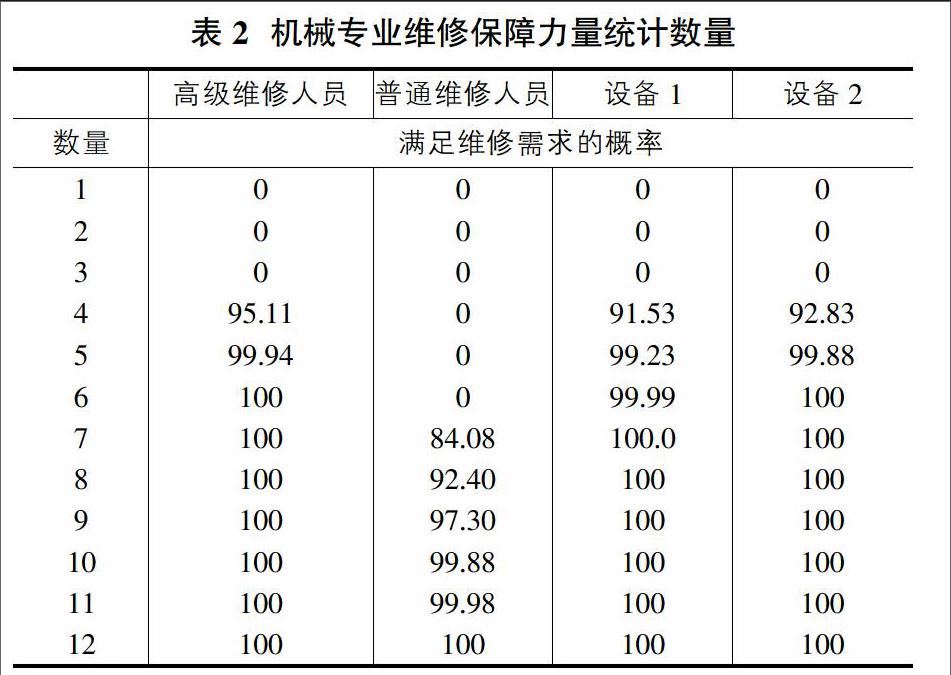
经过大量的蒙特卡洛仿真后,可得到机械专业各种设备各等级维修人员需求的分布,进行10000次蒙特卡洛仿真后情况如表2所示。从表中可以看出当维修人员或维修设备的数量小到一定程度时,不能按要求完成维修任务,随着维修保障人员和维修保障设备数量的增加,超过一定数值后能以一定概率满足最大的维修保障力量需求。当维修保障力量继续增长,达一定界限后,会达到饱和,即能100%的完成维修保障任務。
从表2中可以看出机械专业普通维修人员从7个人开始可以84.08%的概率满足维修所需的最大人数,到12人的时候可以100%的满足维修所需最大人数。高级维修人员从4人开始可以95.11%的概率满足维修所需的最大人数,到6人便能100%的满足维修所需的最大人数。说明高级维修人员维修任务量较为稳定,普通维修工人的维修工作量不稳定,这与实际中机械维修部件较多,装备分解后可以允许较多的人员共同参与维修任务,需求人数会有一个变化的过程相一致,同理维修设备也存在类似情况。
3.2 维修保障力量的数量选取
得到各种维修人员和维修设备的数量分布后,可以根据需要确定出维修人员和维修设备数量。在确定数量过程中需要考虑满足度和数量变化的敏感程度。满足程度即在该数量下能完全满足需求的概率,通过数量分布可以查找,例如机械专业普通维修人员取数量为7的时候,满足数量需求的概率仅为84.08。敏感程度即在当前数量下减少1个数量后满足程度下降的幅度大小,下降大则敏感下降小则不敏感,例如机械维修专业普通人员数量取8人时其满足程度为92.40%,若此时减少一人变成7个,满足程度变为84.08%,下降较大。若取11人,人数减少1个满足程度降到99.88%,仅较小0.1%,那么这时敏感程度较较小。
满足程度即数量分布用?着表示,设其阈值?着0,当?着?叟?着0即可认为满足需求。
某专业维修人员或维修设备的敏感程度用?琢表示:
?琢=?着i-?着i-1
?着i——某设备或人员取数量i时的满足程度;
?着i-1——某设备或人员取数量比i少1个时的满足程度。
不同设备或是不同专业维修人员的变化敏感程度不同,因此选取设备或人员数量时需要设定敏感程度的极限值?琢0,应当选取?琢?燮?琢0的数量,当使维修人员或维修设备对数量的变化不那么敏感。
假定选择?着0=95%,?琢0=5%,根据仿真的结果我们选取机械专业维修人员和维修设备数量汇总在表3中。
4 结论
采用蒙特卡洛仿真的方法对维修保障人员和维修设备的数量进行了仿真计算。通过大量的仿真,得出了在维修人员和维修设备的分布情况,并建立了依据满足维修的程度和敏感性确定维修人员和设备的数量的选取法则。蒙特卡洛仿真很好地解决了多种维修保障资源、多因素同时进行优化的难题。蒙特卡洛法可直接获得整数结果,计算中没有四舍五入,比一般线性计算公式更容易获得较精确地维修保障力量数量。
参考文献:
[1]罗祎,苏执阳,阮文智,等.军用装备维修保障资源预测与配置技术[M].北京:兵器工业出版社,2015.
[2]孙宝琛,贾希胜,程中华.战时装备维修保障资源优化模型[J].火力指挥与控制,2013,38(6):159-163.
[3]孙宝琛,贾希胜,王亚彬.基于蚁群算法的维修保障资源应急调度研究[J].国防交通工程与技术,2012(6):37-43.
[4]张波,于永利,徐英,等.基于排队论的装备维修保障过程分析[J].装备指挥技术学院学报,2012,23(1):114-119.
[5]赵倩,董冬梅,姜桂河,等.作战仿真数据的量化与分析[M]. 北京:国防工业出版社,2015.
[6]刘思峰,方志耕,朱建军,等.系统建模与仿真[M].北京:科学出版社,2012.endprint

