级间分离中的参数不确定性对箭体响应的影响

熊旭军

【摘 要】多级火箭的级间分离过程中具有不确定性的箭体模型参数（如质量特性、初始条件、分离机构参数等），外激励可能的偏心对箭体载荷的准确分析具有重要影响。为了考虑在这种不确定性下的任意组合条件下的箭体响应特性，在结构载荷分析中，本文结合Monte Carlo技术，研究了在冷、热两种级间分离方式下，推力偏心量的不确定性和分离过程中的质量时变性对箭体响应的影响。通过Monte Carlo模拟，预测分离参数具有不确定性下的响应统计结果，以评估工程实际中的不同分离方式下的负载情形。

【关键词】火箭载荷计算；热分离；冷分离；参数不确定性；蒙特卡洛

【Abstract】The difficulty in dynamics analysis of stage separation lies not only in the uncertainty of model parameters （mass properties， initial conditions， separation mechanism parameters， etc.）， but also the uncertainty of the thrust eccentric. In order to account for the randomness response characteristics of the multistage launch vehicle under multiple uncertainty conditions， Monte Carlo technique was employed in the stage separation analysis. This paper studied how the uncertainty of the amount of thrust eccentricity and separation process quality variability affect the dynamics response of the multistage launch vehicle under both cold separation and hot separation conditions of multistage launch vehicles. Through Monte Carlo simulation， this paper forecasts separation parameters response statistical results under uncertainty to assess the actual load situation in the different projects under separate ways.

【Key words】Rocket dynamics analysis； Hot separation； Cold separation； Parameter uncertainty； Monte Carlo

0 引言

结构动力学分析是火箭设计中的一个重要环节，其目的是为以后的火箭结构设计和各部段强度计算提供依据。由于运载能力和多级火箭技术的不断提升，使得我们不得不对火箭级间分离这一复杂过程进行细致的研究。Jeyakumar和Biswas[1]提出利用四阶龙格-库塔方法来求解分离体的非线性微分方程。Michael和Charles[2]给出了高空级间分离前后的羽流冲击力。Saxena[3]研究了上面级火箭对分离助推器的喷射冲击作用。鲁昌鑑和朱礼文[4]采用有限元逐步积分的方法，计算了一、二级热分离时结构的纵向响应。并且在进行具体计算时，为了避免分离时外载荷突变造成的不稳定性，而进行了变步长计算处理。王锋[5]建立了火箭冷、热两种分离形式下的边界处理情况。

通过利用现有的实测技术和相关理论成果，能很好的分析理想化条件下的火箭级间分离载荷。然而，由于不同的分离机制和分离干扰的存在，使得结构和载荷的各个参数会在一定范围内变化，并且影响着整个分离过程。在工程实际中，利用概率随机分析不确定性结构非常重要。最常用的方法往往是将结构的几何尺寸、材料参数等的不确定性视为随机变量，这样结构参数的概率信息便可通过参数的均值、标准方差和协方差来表示。

在对具有随机参数的结构动态特性分析中，随机因子法[6]、随机有限元法与摄动法[7]、正交展开与扩阶系统法[8]、概率密度演化法[9]和Monte Carlo法[10]被广泛使用。Monte Carlo法是将结构参数纳入一个给定的变化范围，并进行大量的动力学分析，最后得到结构固有频率和固有振型的均值和标准差，由于是通过求解大量样本值而获得统计特性的方法，所以Monte Carlo法计算量大。但因此得到的解一般被视为准确解。

Roshanian和Talebi[11]利用Monte Carlo仿真，分析了各种扰动（如动态不平衡、剩余推力、分離机构引起的分离扰动，以及冷、热分离未对准）对分离的影响。Reubush[12]等用Monte Carlo模拟了美国国家航空航天局高超声速试验机（Hyper-X）的级间分离。

1 理论与方法

1.1 级间分离描述

火箭级间分离通常包含冷分离和热分离两种分离模式。

冷分离是下面级先关机，然后两级分离，分离后上面级再点火，三个过程分开进行。相对于热分离模式，级间冷分离有级间结构不受高温排气等优点，但冷分离失控时间长、分离干扰大，影响上面级飞行初始稳定，严重时助推级可能会出现"回追"现象碰到二级段。

热分离是在下面级分离之前上面级就已经点火，然后下面级分离抛掉，上面级继续飞行。是一种在短时间内下面级关机、上面级点火、两级分离的比较复杂的过程。热分离的分离力主要来自上面级发动机喷流对下面级的作用力。

1.2 级间分离计算处理

在计算箭体纵向结构振动响应时，建立相应的质量-弹簧模型，如图1所示。当计算到分离时刻时，方程中的各系数矩阵（质量矩阵、阻尼矩阵和刚度矩阵）及载荷项都发生变化。

级间分离计算处理：设自由度为N，分离面位于箭体中间部位，其连接刚度为Kl，阻尼系数为Cl，分离时刻为Ts，则处理如下：

1）质量矩阵、阻尼矩阵和刚度矩阵去掉后面的N-s行和列。

2）刚度矩阵和阻尼矩阵第s个对角线元素做如下改变：

3）方程右端载荷向量去掉后面的N-s个元素，并做如下变换：

1.4 Monte Carlo模拟流程

利用Monte Carlo模拟仿真来分析级间分离过程中的参数不确定性对箭体响应的影响。流程图如图2所示。

2 算例分析与讨论

2.1 模型计算参数

考虑两级火箭的级间分离过程。相应的级间分离参数如表1所示。

火箭级间冷分离推力模型如图3所示，热分离推力模型如图4所示。相比于冷分离推力模型，热分离过程中上面级发动机在分离前就已点火、工作。

2.2 级间分离响应分析

通过对箭体分离前后进行模态分析，得到火箭级间分离前、后纵向振动的前六阶振型图如图5、圖6所示。

火箭级间冷分离过程中各节点位移响应图如图7所示，各截面轴力图如图8所示。

火箭级间热分离过程中各节点位移响应图如图9所示，各截面轴力图如图10所示。

冷、热分离过程中的位移响应图在分离时刻均发生了突变，这是基于参考点的变化而产生的，分离前以火箭底面为参考基准点，而分离后以分离面为基准点。冷、热分离过程中的各截面轴力图在分离时刻也发生了突变，这是由于在分离时刻发动机均未达到最佳工作状态。

2.3 Monte Carlo模拟不确定性参数组合下的响应

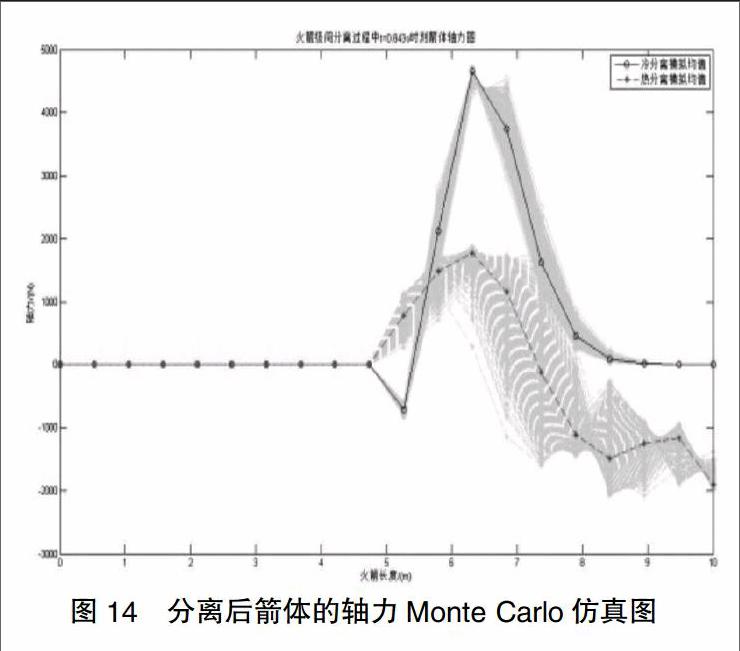
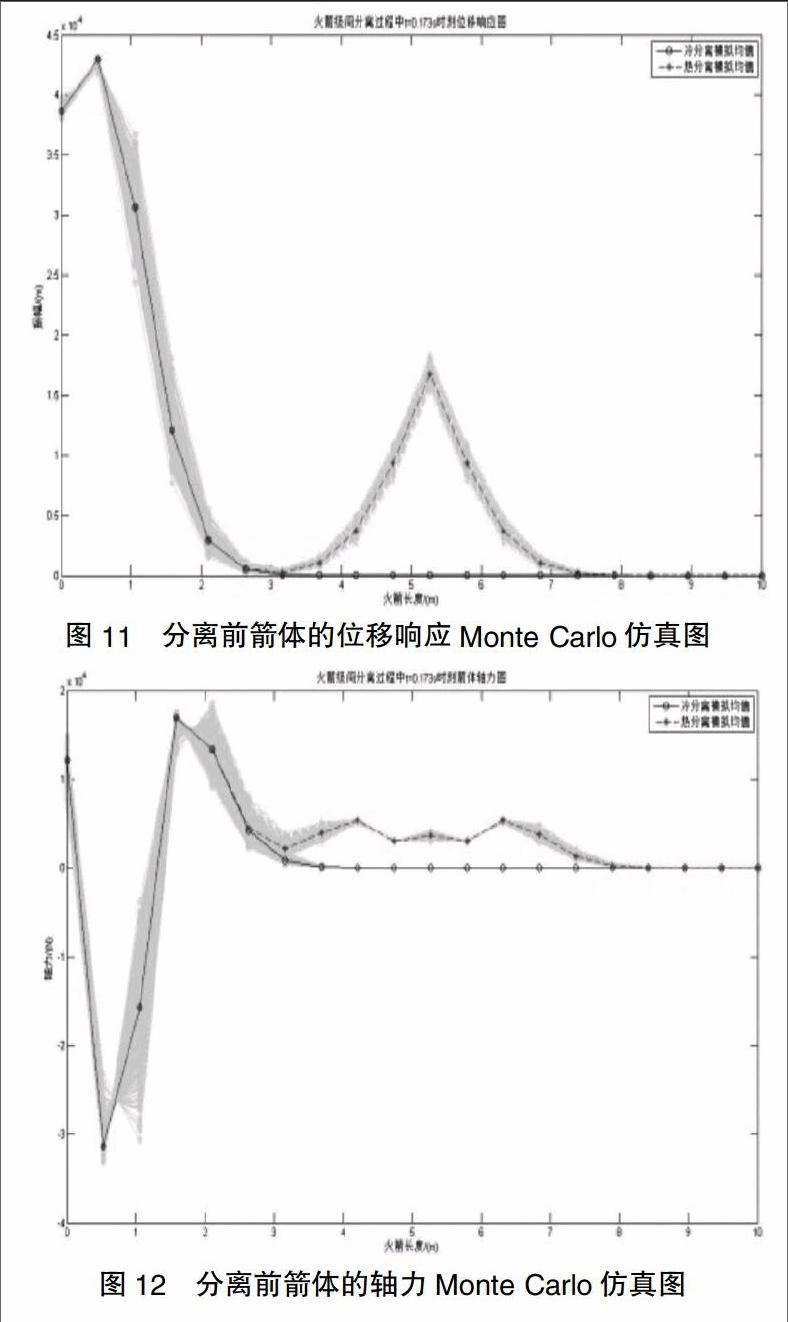
火箭级间冷、热分离前位移响应图如图11所示，截面轴力图如图12所示。从图中可知在箭体的末端两种分离方式下的箭体位移响应及箭体轴力一致，但冷分离方式下的响应很快趋于零，而热分离方式下的响应仍有一个振荡过程。在不确定性参数的影响下热分离方式的偏差要明显大于冷分离方式。

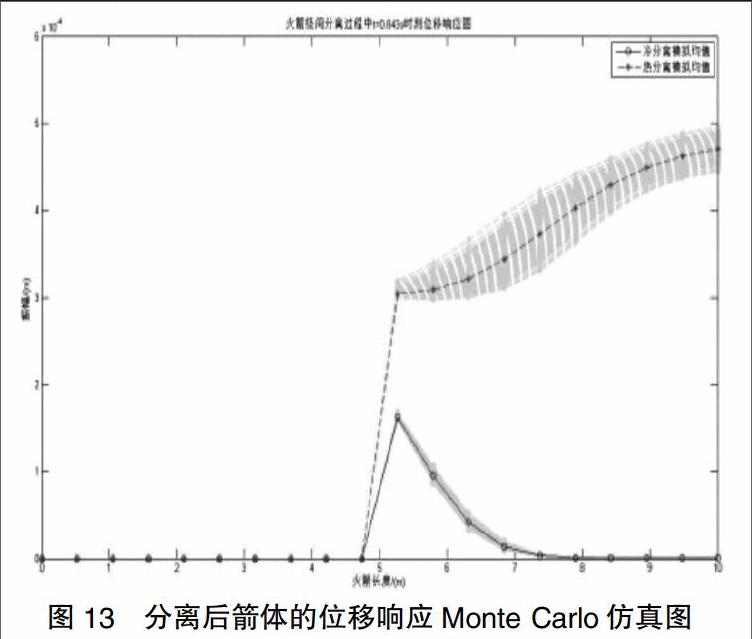
火箭级间冷、热分离后位移响应图如图13所示，截面轴力图如图14所示。由于发生了级间分离，箭体末端被抛掉，所以图中所示箭体中段以后响应均为零。相比于分离前，分离后的箭体响应幅值要更小些，由于图中坐标量级的不一致而导致产生视觉误差。可以发现分离后热分离的偏差还是要高于冷分离。

3 结论

本文采用了Monte Carlo数值仿真方法，来模拟火箭级间分离过程中的动态参数对箭体响应的影响。在动态参数的分析中，考虑了火箭推力具有随机性的偏心量和箭体分离过程中的质量变动。对于箭体结构的响应分析则主要考虑纵向响应计算，并简化为质量-弹簧模型，利用有限元逐步积分思路进行分析。计算结果表明：

（1）冷、热分离瞬间箭体各节点位移及各截面轴力均发生了突变。

（2）在具有高斯分布的选定参数下，热分离过程中的箭体位移和轴力偏差均比冷分离过程中的响应偏差大。

（3）在具有高斯分布的选定参数下，火箭级间分离前的响应偏差均比分离后的响应偏差大。

【参考文献】

[1]Jeyakumar D， Biswas K K. Stage Separation Dynamic Analysis of Upper Stage of a Multistage Launch Vehicle using Retro Rockets[J].Mathematical and computer modelling， 2005，41（8）：849-866.

[2]Su M W， MULLEN C R. Plume Impingement Force during Tandem Stage Separation at High Altitudes[J].Journal of Spacecraft and Rockets，1972，9（9）：715-717.

[3]Saxena S K. Upper Stage Jet Impingement on Separated Booster[J].Aeronautical Journal，1979，83（818）：71-74.

[4]鲁昌鑑，朱礼文.运载火箭热分离时结构纵向响应计算[J].强度与环境，1979，3：26-45.

[5]王锋.运载火箭载荷计算及通用软件实现[D].国防科技大学，2001

[6]Chen J J，Chen J W，Sun H A，et al.Probabilistic Dynamic Analysis of Truss Structures[J].Structural Engineering&Mechanics，2002，13（2）：231-239.

[7]郭书祥，冯元生，吕震宙.随机有限元方法与结构可靠性[J].力学进展，2000，30（3）：343-350.

[8]李杰.随机结构系统-分析与建模[M].北京：科学出版社，1996.

[9]李杰，陈建兵.随机结构反应的概率密度演化分析[J].同济大学学报，2003，31（12）：1387-1391.

[10]Niederreiter H， Spanier J. Monte Carlo and Quasi-Monte Carlo Methods[M].Berlin：Springer， 2000.

[11]Roshanian J，Talebi M. Monte Carlo Simulation of Stage Separation Dynamics of a Multistage Launch Vehicle[J].Applied Mathematics and Mechanics，2008，29（11）：1411-1426.

[12]Reubush D E， Martin J G， Robinson J S，et al.Hyper-X Stage Separation Simulation Development and Results[C].10th International Space Planes and Hypersonic Systems and Technologies Conference，Kyoto，Japan.2001.

[责任编辑：朱丽娜]