基于一维非稳态传热模型的炉温曲线优化研究

张晓果，路 月，林宗明，李政君,杜亚冰，兰奇逊

(1.河南城建学院 数理学院，河南 平顶山 467036； 2.河南城建学院 能源与建筑环境工程学院，河南 平顶山 467036; 3.河南城建学院 电气与控制工程学院，河南 平顶山 467036)

回流焊技术作为电子产品生产过程中的重要环节，通过控制回焊炉各部分的温度，在保持工艺要求的同时，来提高产品的质量一直是现代电子工业亟待突破的课题[1]。李岩等[2]对某型回流焊炉进行分析，阐述了其炉温曲线设定的方法，并引入加热因子等相关概念对原温度参数进行优化；冯志刚等[3]分析了回焊炉中工艺参数对炉温曲线的影响，得到炉温和传送带速度两个关键影响指标，并对指标进行深层次研究；龚雨兵[4]以最大热应力为优化目标，对回流焊温度场进行数值建模与仿真，得到最优温度分布及热应力分布；朱桂兵等[5]以助焊剂活性导致焊接缺陷的角度反推温度曲线设置的不合理性，结合热效能理念寻求解决办法。以上研究大多都是直接从工艺参数的机理入手，结合不同加工工艺要求，分析影响温度曲线的主导因素，以该主导因素为变量进行相应的灵敏度分析。但实际上,盲目试验不仅增加工作量，而且还需通过测试数据来设置工艺参数，以实现要求的炉温曲线效果。汪学军[6]从实际应用出发，以能量守恒定律与傅里叶定律的热平衡机理为依据对焊接过程进行分析，建立了一种全新的多温区自动整定策略，通过自学力能力对控制参数进行了优化，找到了较好的控制参数。但是，通过数值模拟对机理模型进一步分析，直接获取回流焊各控制参数以及对炉温曲线进行数值优化的工作目前仍比较欠缺。

本文首先对某回焊炉各温区的温度与时间变化进行线性回归，并对焊接过程温度场进行有限元分析，发现对流传热系数为关键性指标，根据炉温设置的特定要求，绘制炉温曲线。然后通过有限差分法更改初始设定的炉温以及传送带速度，对原有炉温曲线进行优化，使得传热系数达到最优，获得最佳指标值，并通过MATLAB进行蒙特卡洛数值模拟检验。研究发现，该方法能有效地减少物理试验次数以获得较优的炉温曲线设置，从而使得炉温设置与焊接机理能更好地关联起来。

1 回焊炉介绍

1.1 回焊炉的组成

选取的回焊炉其内部由炉前区域、炉后区域及11个小温区构成，其中各小温区长度均为30.5 cm，相邻间隙为5.0 cm,在加热区外有炉前、炉后两长度为25 cm的区域，如图1所示。从其截面角度观察，回焊炉内部又分为4个功能区(大温区)：预热区、恒温区、回流区、冷却区。

图1 回焊炉截面示意图

1.2 炉温分布及设置

假设回流焊炉内空气温度短时间能达到稳定，处于正常工作状态,各温区设定炉温即为炉内热风温度。在回焊炉工艺焊接过程中，炉温曲线需满足不同工艺的要求，相关变量有相应的制程界限，具体见表1。将传送带速度初始设定为70 cm/min。各温区温度设定值分别为175 ℃(小温区1～5)、195 ℃(小温区6)、235 ℃(小温区7)、255 ℃(小温区8～9)及25 ℃(小温区10～11)。

表1 炉温曲线的制程界限

1.3 实际问题的数学化处理

如图2所示，电路板在回焊炉内焊接时，其受热情况实际上是三维立体温度扩散，假设热辐射的影响极小，因此可忽略平行板的高度和宽度，将立体平行板简化为只与厚度有关的一维空间。回焊炉各功能区温度曲线分布如图3所示。本文需要解决的问题就是通过建立合适的数学模型，在设定传送带速度和各温区炉温的前提下，求得炉温曲线的温度分布，并在建模基础上进一步优化炉温曲线，在符合制程界限条件下，求得最大过炉速度，从而在保证产品质量的同时又提高其加工效率。

图2 回焊炉中电路板的受热情况

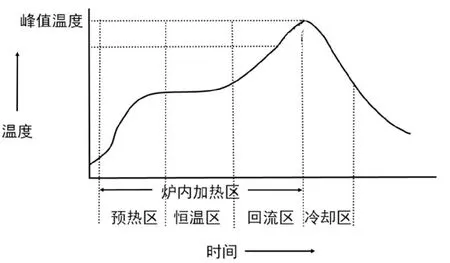
图3 炉温曲线各温区分布

2 炉温曲线建模及机理分析

2.1 基于热传导方程的炉温建模

在回流焊接过程中，其热量Q的传递主要由对流换热Qc、辐射换热Qr和热传导Qk三种基本传热方式组成，满足能量守恒定律[4]：

Q=Qc+Qr+Qk

(1)

单位时间内通过单位面积的流体质量由温度T1流至T2处所传递的热量为：

Qc=CpM(T1-T2)

(2)

其中，Cp是定压比热容，M是流体质量。

对流传热受多种因素影响，主要考虑流体与物体接触面的热交换,即电路板表面与热风的对流换热量。牛顿冷却公式[6]为：

Qc=hΔTA

(3)

其中，h是对流传热系数，ΔT表示平壁两侧温差，A是发生对流的面积。

为了推导物体热交换的微分方程,应根据质量守恒定律和傅里叶定律来建立物体中的导热温度。导热物体各方向热流量可分解为x,y,z三个坐标轴方向的分热流量，通过y-z、x-z、x-y三个微元表面导入微元体热流量分别用qx、qy、qz来表示，根据傅里叶定律[7]得出：

(4)

假设各分层内不含热源，故可忽略介质比热和密度的影响，在三维等方向均匀介质中的热传导方程需满足：

(5)

为了进一步简化模型，可将各分层视为无限大，仅考虑在厚度方向即x方向上的温度变化，便可将式(5)化简为：

(6)

其中，λ是热导率，α是介质热扩散率，T表示电子元件的中心温度。

2.2 分段线性回归分析

假设x是时间，为自变量；y是温度，为因变量。

yi=β0+β1x1+μ

(7)

其中，β0和β1为回归系数，μ为无法预测的且满足一定条件的扰动项。

原假设H0：联合显著性检验β1=0。

根据各温区温度随时间的变化关系进行分段线性回归，采用OLS最小二乘估计法，确定各温区的回归系数，如表2所示。

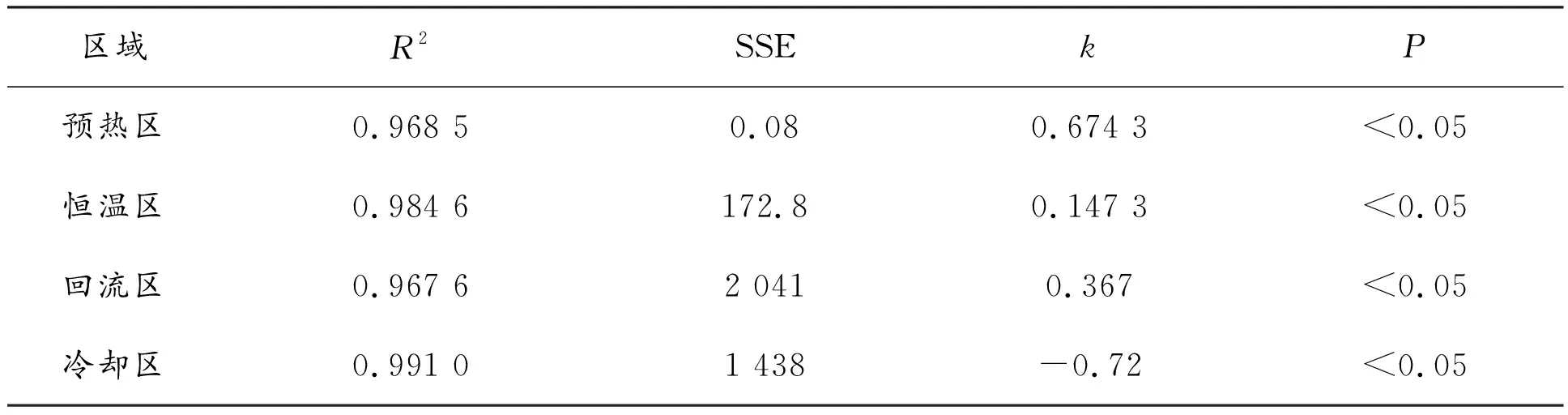
表2 回归系数表

由表2可知:拟合优度R2均接近于1，且P小于0.05，说明可以拒绝原假设，回归性显著。按照上述方法将各段位置温度的不同影响代入不同的控制温度点，进一步建立线性关系，用MATLAB绘制炉温曲线如图4所示。由图4可知:在升温过程中，得到模型结果的温度随时间变化率的线性拟合效果较好；而在降温过程中，拟合数据的温度下降速度略慢于实际数据的下降速度，使得曲线后半部分存在略微差异。考虑到上文中提到的制程界限对温度下降速率存在一定影响，因此使得模型中得到的降温过程中的炉温曲线受到了相应限制，这也是模型的合理之处。

图4 炉温拟合曲线对比图

2.3 有限元分析结果

(1)绘图

绘制单个焊炉的三维几何模型，见图5。焊接回流的内部近似一个长方体，高温气流从焊炉上方的风机流出，对流换热后被下面的吸收器吸收，电子元件从左侧的间隙进入，接受管内高温气流对流传热，随传送带从右侧间隙进入下一个焊炉，因为炉内高温气体均匀，因此忽略焊炉高度对气流的影响。单个焊炉的几何长度为30.5 cm，横截面为圆形，直径为15 cm。

图5 单个焊炉的三维几何模型

设置左侧电子元件入口为低温入口，右侧为高温出口，高温气体从上方吹出，设置method的流体条件，设置除元件入口、出口外的几何外壁的膨胀层，然后划分网格。通过网格划分将几何体分解为多个单元格，让计算机在不同的单元格中模拟分析，增加结果的稳定性，使结果收敛，防止模拟数据失真。

(3)前处理

设置气流的流速、温度、动力黏度系数，设置入口温度和物体速度。

(4)后处理

模拟炉内稳定温度时的温度云图，并由ANSYS软件求解绘制温度折线如图6所示。

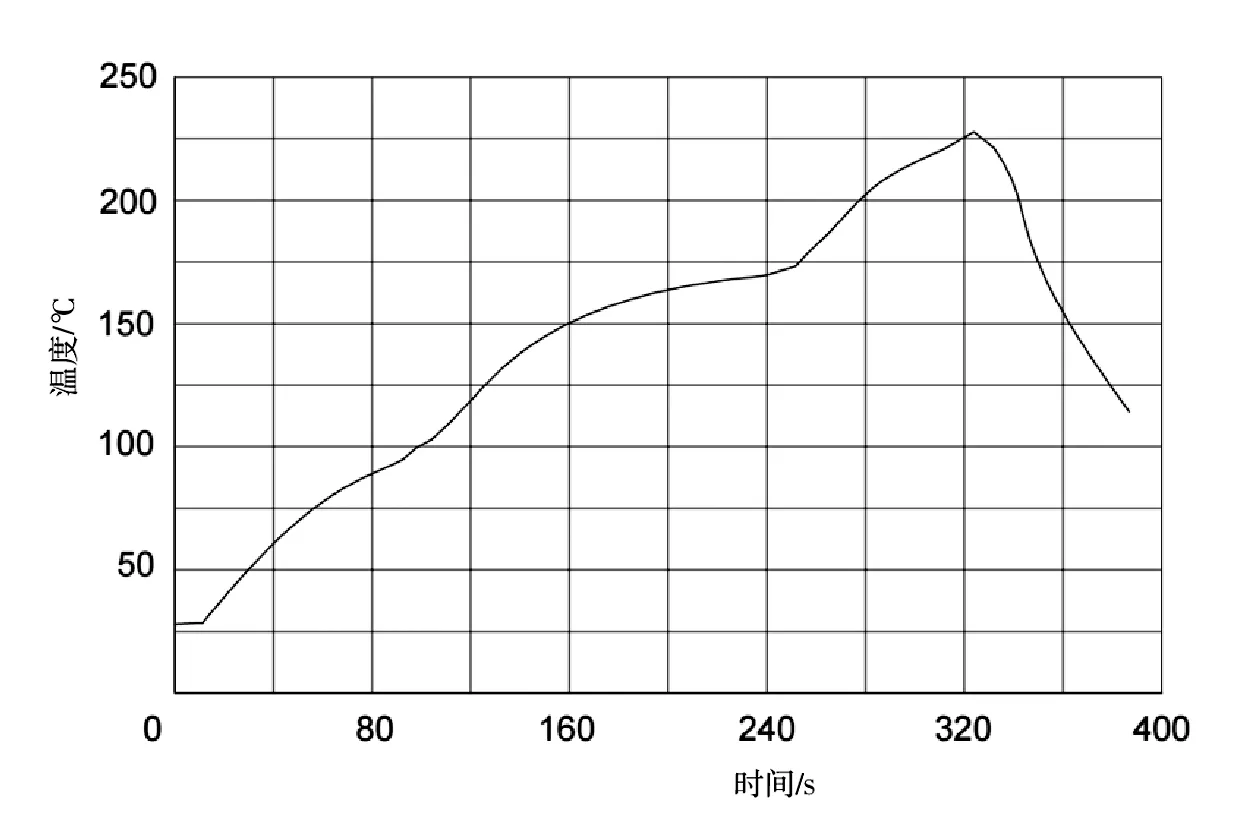
图6 温度折线图

通过单个焊炉的温度轮廓如图7所示，分析炉中温度变化，得到电子元件加热焊接的直观图像，使温度变化梯度可视化，并与模拟数据对比，校验模拟数据。

她死得很安详。四年时间足以让她面对现实。并且，某一天，她突然惊喜地发现，她再一次迎来了久违的爱情——从未被设计和植入的爱情——真正的爱情。她爱上秦川，玩偶爱上玩偶，这感觉让她战栗。

图7 温度轮廓图

由图7可以看出，物体进入开口后受到炉内高温气体的对流换热，吸收炉内高温气流热量，造成炉内温度分布不均匀，但在工作时炉内温度趋于稳定。

3 机理模型下的炉温曲线优化

3.1 一维非稳态传热模型的建立

在热传导方程基础上，根据傅里叶定律和能量守恒定律，在任一时间间隔内有如下热平衡关系：导入微元体的总热流量=导出微元体的总热流量+微元体内热力学能的增量。

其控制方程[8]为：

(8)

其中，ρ是密度，c是比热容。

对于整个炉内传热模型，属于第三类边界条件，对流换热对物体提供热量，假设在高温环境下，炉内温度分布的初始值为当前温区温度。边界条件和初始条件满足：

(9)

其中，L是导热长度，Tlu是炉内温度，T0是环境温度。

在非稳态一维传热模型中，通过建立最小二乘法估计换热系数参数：

(10)

3.2 有限差分法求解

传热模型求解的基本思想是把空间、时间上相同且连续的物理系数离散化，利用有限差分法进行数值计算求解。使用显式差分对传热模型模拟离散，假设物体各个方向传热为各向同性，由牛顿冷却公式联立方程计算求解第(n+1)时间轴上的温度Tn+1，依靠前一层的温度大小，控制方程离散其中的未知量。

(11)

对一维非稳态传热模型进行离散化后，由设立的边界条件和初始值，在不同的时间和空间节点上进行分层离散求解，建立未知值和元件中心温度值的关系，进而搜索元件的热导率，求解拟合温度数据的最优组合，具体步骤为：

(1)代入炉温的初始值，通过模型离散方程逐层求解，得到元件中心温度的h值；

(2)更新温度值，迭代离散方程进行求解，得到优化后的h值；

(3)遍历新的温度值，全局搜索拟合程度最佳且满足制程界限的对流传热系数，并确定最优指标值；

(4)根据最佳对流传热系数组合，得到元件中心温度分布。

3.3 结果分析

根据上述方法求得各小温区最佳对流传热系数下的最优温度及最快过炉速度，见表3。

表3 最优炉温曲线的指标值

优化目标函数 (最优传热系数) 的优化历程如图8所示。

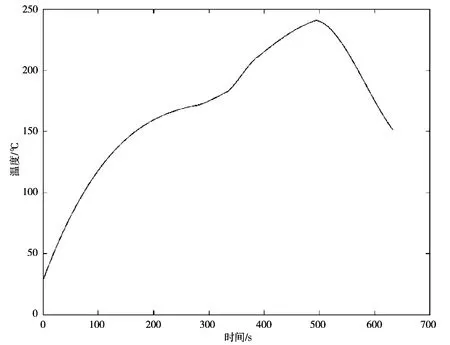
图8 最优传热系数下的优化曲线

由图8可看出,各个小温区温度(除冷却区之外)相较于最初设定温度均有相应的改变，原因是冷却区温度确定之后，对应的温度时间便可求得，利用有限差分法和递推公式对其他温区进行刻画，使得优化曲线更为平滑，连续性更好。与基于热传导方程的模型相比，该模型保证了各功能区温度过渡的连贯性。

3.4 蒙特卡洛模拟检验

考虑到传送带的速度限制会对炉温曲线的变化造成影响，为了提高模型数据的准确性还可以进行蒙特卡洛模拟。先将速度区间离散化，然后基于传热模型，遍历传热过程中每个传送带速度，得到相应的温度分布，代入约束条件进行检验，最后求得决策后的最优传热系数下的最大速度。

最优传热系数下的约束条件：

(12)

其中，T(tj)为在第j个时间微元下的温度(j=1,2,3…)。

根据上述约束条件，提出一种搜索算法，其过程如下：

Step1：确定速度初始区间v∈[65,100]，令v=100；

Step2：绘制当前传送带速度下的炉温曲线；

Step3：验证约束条件(式(12))，直到当前速度为允许最大过炉速度时结束，否则Step4；

Step4：设置步长为1，即v=v-1，更新搜索区间，回到Step2继续循环。

根据以上搜索算法，依次迭代求得满足加工条件的最优炉温曲线，对升、降速度进行求解，利用MATLAB软件编程得到决策后的最优传热系数下的最大过炉速度为76 cm/min，并绘制出当前速度下温度分布曲线，如图9所示。结果发现与有限差分法所求解的结果基本相符，从而通过了一致性检验，同时也说明基于有限差分法的传热模型符合优化目标参数的求解。

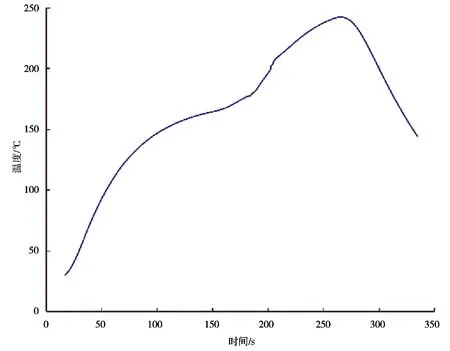
图9 v=76 cm/min时的炉温曲线图

4 结论

通过建立一维非稳态传热模型，以最优传热系数为优化目标，利用有限差分法和递推公式对已有的炉温曲线进一步优化，再通过蒙特卡洛模拟证明模型的有效性，主要结论如下：

(1)利用有限元分析温度轮廓图可知，物体的进入使得温度场紊乱，在工作情况下温度趋于稳定，且温度变化趋势很小，可以忽略温度场不均匀的导热对物体温度变化的影响；

(2)非稳态传热模型相较于基于热传导方程下的分段线性回归模型，其温度随时间的变化率在各功能区内不定，随环境变化的自适应性较强，优化后的曲线更为平滑；

(3)基本上解决了回归过程中存在的内生性问题，保证了各功能区温度过渡的连贯性，借用该模型可大大减少物理试验次数而获得可行的炉温曲线，并能通过优化获得特定制程界限下的最优炉温曲线设置。