锂离子电池组分层主动均衡研究
聂伟民,陈自强
(上海交通大学 a.海洋工程国家重点实验室 b.高新船舶与深海开发装备协同创新中心,上海 200240)
锂离子电池因为具有能量密度高、可靠性强、循环寿命长、对环境污染小等优点,目前被广泛作为各类装备的主要能源[1-2]。为了满足各类装备电压要求,需将多节单体锂离子电池串联成组来使用[3]。由于锂离子电池的制造工艺、运行工况以及工作环境等存在一定的差异,导致成组后电池单体以不同的速率衰退,从而造成电池的内阻、容量以及电压产生不一致性,使得电池组整组性能差于组内单体电池性能总和,最终导致电池过快衰老、退役,并会对环境造成影响[4]。为了有效解决电池组不一致性问题,均衡控制是必不可少的手段,即在有效的均衡构架中,利用均衡拓扑电路和有效的控制策略来实现电池组均衡[5]。
主动均衡中常用的均衡构架包括[6]:相邻电池单体均衡构架、任意电池单体间均衡构架以及电池单体到电池组均衡构架等。基于相邻电池均衡构架,Rahimi A M[7]提出了基于开关电容转换器的均衡电路,该方法是借助相邻单体电池间的公共电容进行能量转移,其电路简单,但无法控制均衡电流,且只能以端电压作为均衡标准。Ye Y[8]和Lee Y S[9]分别应用Buck-Boost和Cuk斩波均衡电路来进行相邻电池单体间的能量转移。这类电路在少量电池间使用效果显著,但是一旦电池数量增多,其效率会明显降低。Mestrallet F等[10]提出了一种采用任意电池间均衡构架的电路,采用了多相桥式转换器,消除大量开关管网络,简化了电路,但是转换器中的MOSFET会承受高压应力,从而导致该电路高成本、低效率的缺点。在基于电池到电池组的均衡构架的研究中,Wei X Z等[11]提出了一种基于反激式变压器的均衡电路,它减少了电压传感器的数量,但变压器中存在的电流返回现象会造成能量损失,并且减少电池使用寿命。其中,相邻单体均衡构架的均衡效率最高,但针对大型装备中大量锂电池串联情况,其均衡速度会受到严重制约[12]。电池单体到电池组的均衡构架具有较快的均衡速度,但其能量损耗较大[13]。因此,文中对分层主动均衡构架展开研究,以SOC作为均衡标准制定均衡策略,并在Matlab/Simulink中搭建模型来验证其均衡效果。
1 动力电池建模及SOC估计
1.1 电池等效电路模型
采用二阶RC等效电路模型来建模,模型如图1所示。Uocv和Ut表示开路电压和端电压;R0表示欧姆内阻;Rp和Cp分别表示极化电阻和极化电容;Rs和Cs分别表示扩散电阻和扩散电容[14]。假定电池组散热良好,忽略温度对电池模型参数的影响。

图1 二阶RC等效电路模型 Fig.1 Second-order RC equivalent circuit model
SOC定义为电池中剩余的可用电量占标称容量的比例,可以表示为:

式中:SOC(0)表示初始SOC值;Cn为电池的额定容量;I为电池电流,这里规定放电时I为负数;η为充放电效率,在锂离子电池中可近似取1。
SOC对时间的导数表示为:

采用放电静置测试获得在25 ℃下的OCV-SOC数据,其拟合特性曲线如图2所示。

图2 OCV-SOC特性曲线 Fig.2 OCV-SOC characteristic curve
1.2 电池模型参数辨识
采用引入遗忘因子(Forgetting Factor)的递推最小二乘法(RLS),对电池模型进行参数辨识,可以解决传统RLS算法中由于数据增长而引起的“数据饱和”现象[15]。
根据二阶RC等效电路模型,可得电池模型的传递函数为:

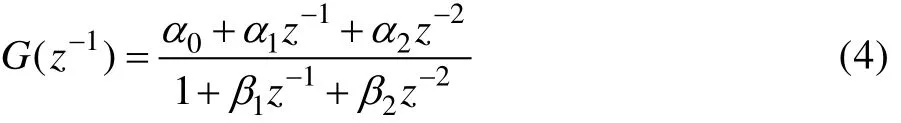
将式(7)离散后的差分方程为:


1.3 电池状态估计
采用FFRLS和扩展Kalman滤波法来联合估算锂离子电池的SOC,流程见表1。其中EKF法是将非线性函数展开成Taylor级数,得到一个近似线性化模型后,再利用Kalman滤波法进行估计[16]。系统的状态空间方程为:

式中:状态向量xk=[SOCkUs,kUp,k]T;wk与vk分别为系统噪声和观测噪声。
该状态空间模型参数A、B以及Jacobian矩阵分别为:
式中:T为系统的采样周期。
2 主动均衡构架及拓扑结构
2.1 分层主动均衡构架
文中提出一种复合主动均衡构架,如图3所示。它是基于相邻电池主动均衡构架和单体电池到电池组主动均衡构架实现的。它将n块电池平均分为m组,每组包含k块电池(n=k·m)。每组内包括k-1个组内均衡电路,每组间包括m个组间均衡电路。
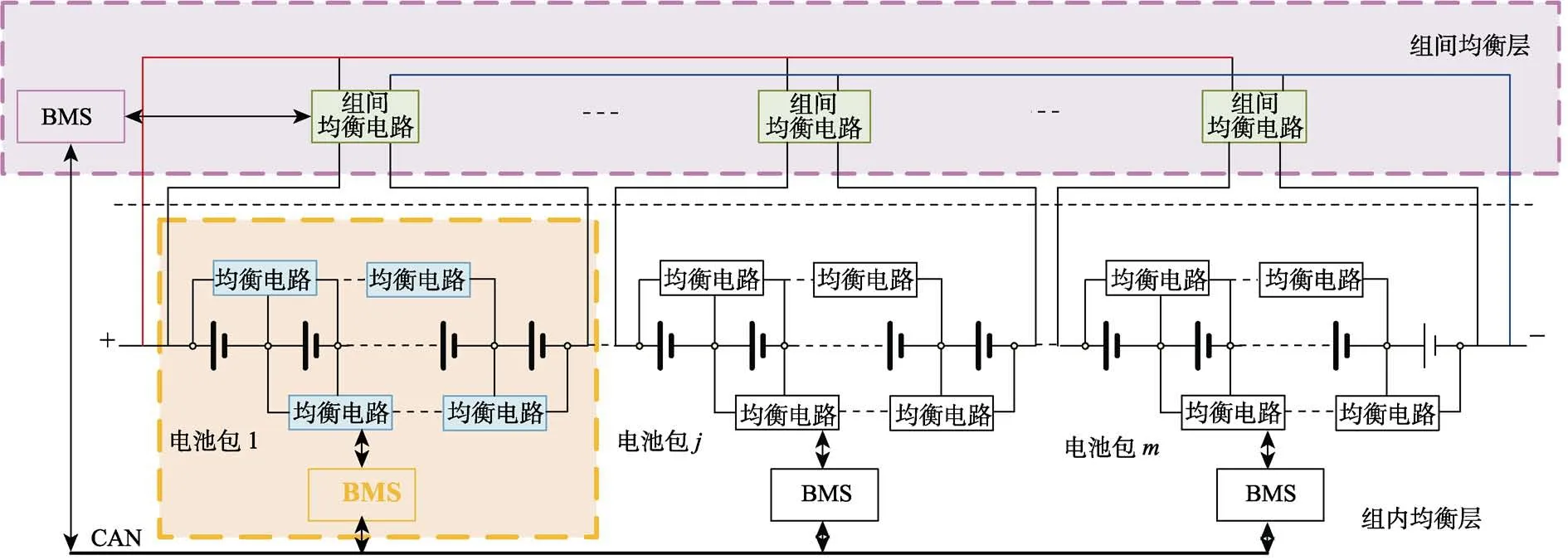
图3 分层主动均衡构架 Fig.3 Hierarchical active balancing architecture
其中,m组锂离子电池组内,均采用相邻电池主动均衡的构架,即组内所有相邻单体电池间都有一个组内均衡电路对单体电池进行均衡,该均衡行为称为组内均衡。另外,将每一组中串联的k块单体电池视为一个整体电池子组,将第一节电池的正极作为电池子组的正极,第k节电池的负极作为电池子组的负极。同时,这m个电池子组采用单体电池到电池组主动均衡构架来进行均衡,该均衡行为称为组间均衡。电池的电流、电压、温度等信息由BMS采集获得,并通过CAN总线传递。
2.2 分层主动均衡拓扑结构
2.2.1 组内均衡拓扑结构
各个电池子组内的Buck-Boost均衡拓扑结构如图4所示。电流经过电感,在电池单体间双向流动[17],并由BMS估算得到单体电池SOC来决策是否进行均衡,再通过PWM波控制Q1、Q2的通断来开启均衡。 当BMS检测到SOC1>SOC2并开启均衡时,PWM波控制Q1。其具体均衡过程为:PWM向Q1输入高电平信号,Q1导通,电流I从电池B1流入到电感L1中储存,此时的电流通路为:B1+→Q1→L1→B1-→B1+;PWM向Q1输入低电平信号,Q1闭合,电感L1产生反向电动势,且持续供流,二极管D2导通,电感L1将储存的能量向B2转移,此时的电流通路为:L1→B2+→B2-→D2→L1,最终完成能量的转移。反之,若要使能量从B2向B1转移,只需对Q2进行控制即可。

图4 Buck-Boost均衡拓扑结构 Fig.4 Buck-Boost balanced topology
2.2.2 组间均衡拓扑结构
电池子组间基于反激式变压器的均衡拓扑结构如图5所示。反激式变压器的原边绕组通过MOSFET与电池子组并接,副边绕组通过MOSFET连接至整个电池组,以反激式变压器为核心,通过磁场和电场的转换来实现能量在电池子组与电池组之间的转移[18]。由BMS估算电池子组的平均SOC,并决策是否进行均衡,再通过PWM波控制Q1与Q2的通断来开启均衡。
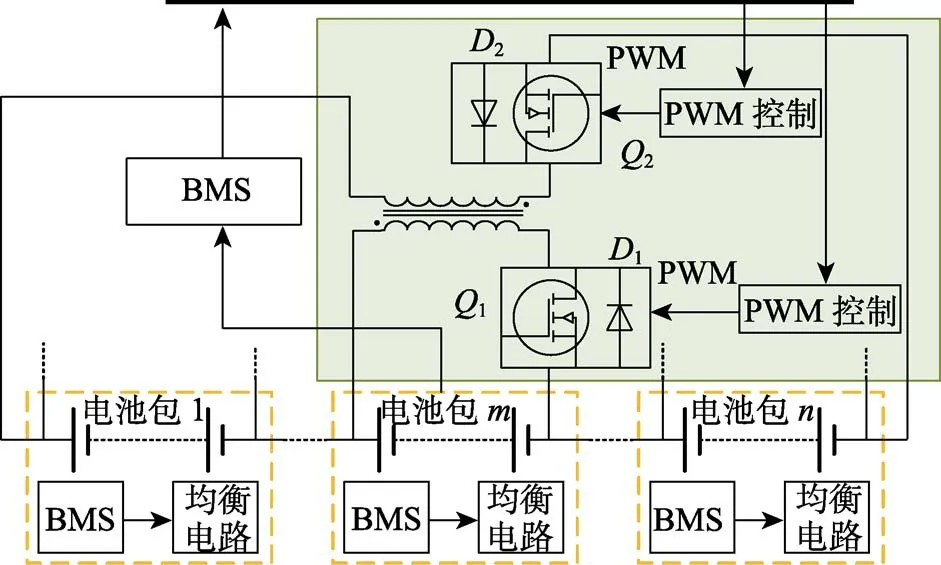
图5 基于反激式变压器的均衡拓扑结构 Fig.5 Balanced topology of flyback transformer
假设BMS检测到某一电池子组m的平均SOC值过高,并决策开启均衡时,PWM波控制Q1。具体过程分析如下:PWM向Q1输入高电平信号,Q1导 通。电池子组m的电压U1加到变压器的原边绕组N1上,副边绕组N2产生的感应电动势的大小为U2。由于二极管D2反向截止,此时的原边绕组相当于一个电感L1来储存电池子组m传递过来的能量。Q1导通至t=To时,原边绕组的电流增加到最大值。该过程通过变压器完成了电能到磁能的转换,此时增加的磁通量为:

PWM向Q1输入低平信号,Q1关闭。原边绕组无电流通过,副边绕组感应电动势,二极管D2导通,能量由电感L2释放,并转移至整个电池组。当t=T时,副边绕组的电流下降到最小值。该过程通过变压器完成了磁能到电能的转换,此时减少的磁通量为:

由变压器的工作原理可知 ΔΦ(+) =ΔΦ(-),因此可得到:

故副边绕组输出的电压值与反激式变压器原副边的匝数比、MOSFET的导通占空比以及原边电压值的大小有关[19]。相反,控制Q2则可实现电池组到电池子组的能量转移过程。
3 均衡策略
文中以电池SOC作为触发主动均衡的条件,此处采用放电均衡为例来说明其均衡策略。基于SOC的均衡策略的流程如图6所示。
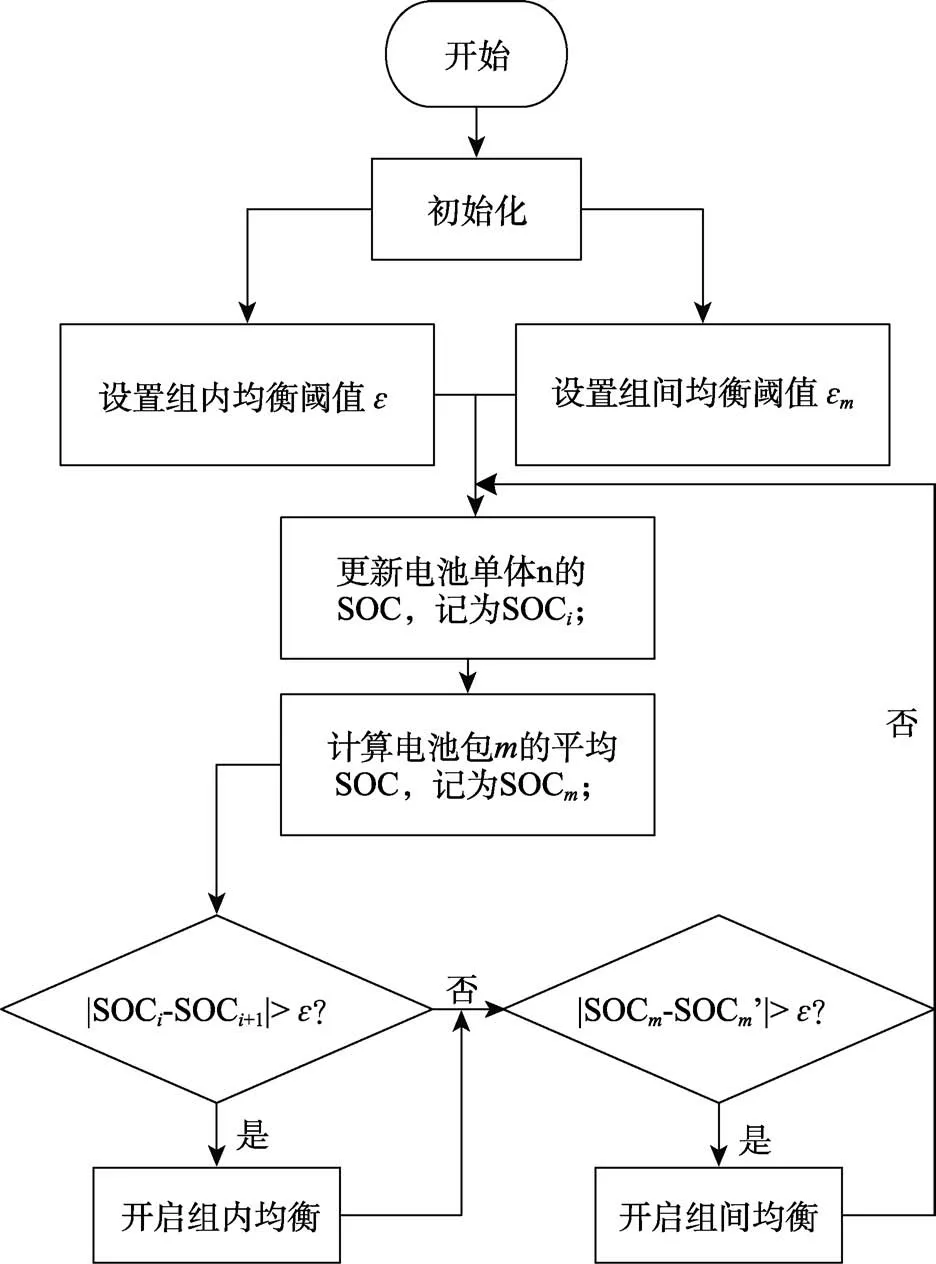
图6 均衡策略流程 Fig.6 Flow chart of balanced strategy
通过测得的电池端电压和电流来估算单体电池的SOC,记为SOCi。根据电池子组内各个单体电池的SOC值,计算出该电池子组的平均SOC,记为SOCm。首先将各个电池子组内单体电池的SOC与相邻单体电池的进行比较,当SOCi与SOCi+1之间的差值大于设定阈值时,开启组内均衡,组内均衡结束后,将电池子组的平均SOC与其他平均SOC最低电池子组进行比较。当SOCm与SOCm′的差值大于设定阈值时,BMS将控制相应的开关管通断,通过反激式变压器来进行组间均衡。
4 实验与均衡仿真分析
实验装置由上位机、Neware BTS4000电池测试平台BLH-100恒温实验箱构成。实验对象为三元锂离子电池,该电池具体参数见表2。

表2 三元锂离子电池参数 Tab.2 The parameters of ternary lithium ion battery
4.1 SOC估计实验验证
4.1.1 SOC估算算法精度
为了验证SOC算法的准确性和有效性,以三元锂电池为实验对象进行FUDS工况(Federal Urban Driving Schedule,美国联邦城市运行工况)测试[20],并保证环境温度为25 ℃恒温。实验中的电压与电流值如图7a所示。采用该数据进行电池SOC的估计,并与真实值对比,如图7b所示。可以看出,SOC估计值与真实值最大偏差不超过1%,所以该算法有较强的精确性。

图7 FUDS工况下SOC估算结果 Fig.7 SOC estimation results under FUDS conditions: a) real value; b) comparison between astimated value and real value
4.1.2 SOC估计算法鲁棒性
设置电池初始SOC为100%,测试时长为1000 s。为了验证算法的收敛性,初始SOC分别取100%、80%、60%、40%、20%、0%。SOC的估计结果如图8所示。由图8可知,在该算法下SOC均能在40 s内快速收敛。
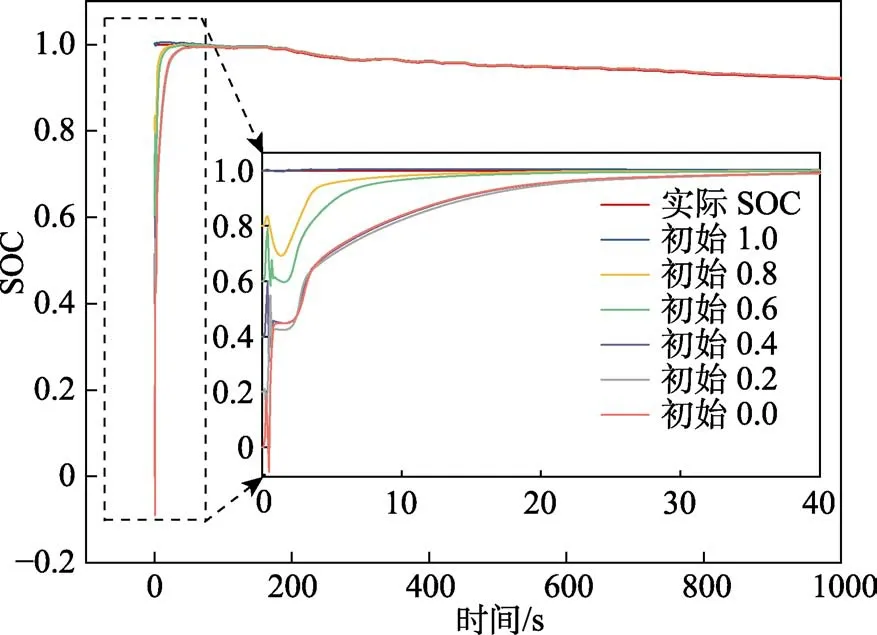
图8 SOC算法鲁棒性验证 Fig.8 SOC algorithm robustness verification
4.2 仿真及结果分析
4.2.1 放电均衡仿真
电池子组1的单体电池初始SOC分别为:98%、96%、92%;电池子组2的单体电池初始SOC分别为:91%、90%、87%;电池子组3的单体电池初始SOC分别为:84%、82%、76%。电池组在FUDS工况下进行仿真实验,未进行均衡的仿真结果如图9所示。由于没有进行均衡控制,9块电池均以相同的速率下降。经过3000 s后,它们的SOC下降了约22.4%,如果继续放电,电池B9会最先放完电而导致电池组停止工作。
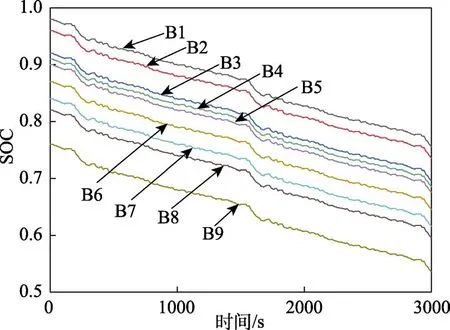
图9 未加均衡结果 Fig.9 Unbalanced simulation results
接下来采用分层主动均衡构架来进行均衡。分层主动均衡构架下的仿真结果如图10a所示。均衡开始前,电池组的初始SOC差值为22%。由于组内单体初始SOC差异大于设定阈值,组内均衡开启。当3个电池子组的组内均衡全部完成后,比较电池子组间的平均SOC值,此时超过设定阈值,组间均衡开启,最终达到均衡进行时间为922 s。从图10a中的均衡曲线可以看出,采用分层主动均衡构架时,各个单体间的SOC值不断接近,减小了不一致性带来的影响,最终单体SOC差异缩小至0.454%。传统相邻主动均衡构架的均衡结果如图10b所示。各电池初始SOC相同。经过1220 s均衡后,电池组中SOC值的差值减小至0.797%。比较两种均衡方式可知,文中提出的均衡构架在均衡效果上提升了43.04%,均衡时间缩短了24.4%。同时根据图11和图12可知,922 s时未进行均衡控制的电池单体的最低SOC值低于均衡后的电池单体SOC值,此时电池组能放出更多的能量。
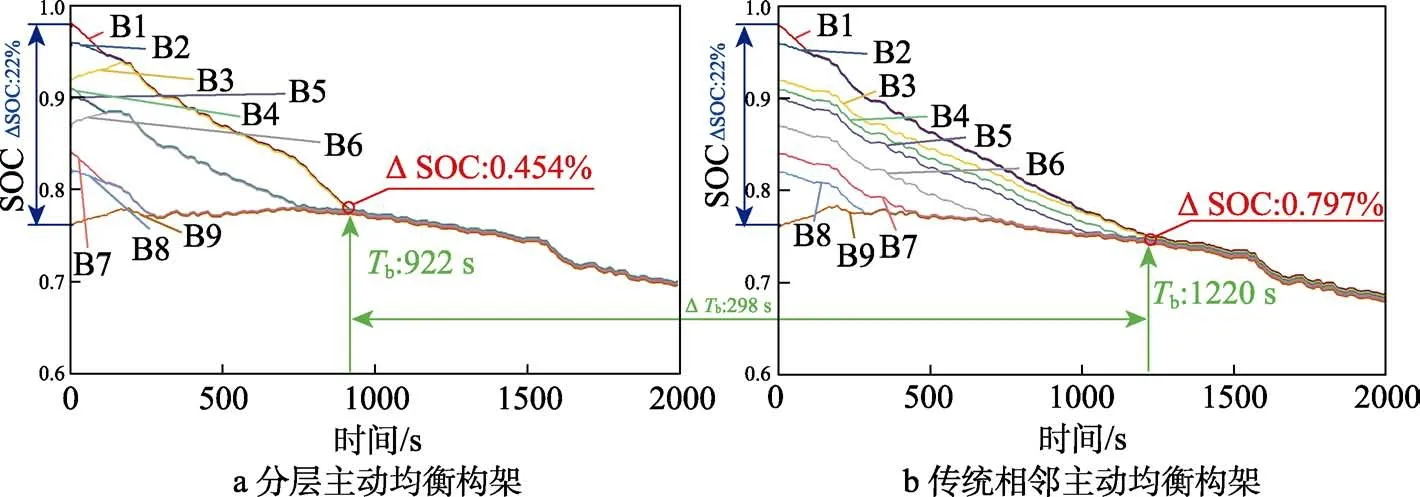
图10 两种构架下的均衡效果 Fig.10 Balancing effect of two frameworks: a) layered active equalization architecture; b) traditional adjacent battery equalization architecture
4.2.2 静置均衡仿真
为了更为直观地体现电池间能量转移的过程,设 置了静置均衡仿真。9块电池的初始SOC值同样为:98%、96%、92%、91%、90%、87%、84%、82%、76%。静置均衡时各个电池SOC变化曲线如图11所示。图11a为分层主动均衡构架下的静置均衡曲线,图11b为传统主动均衡构架下的静置均衡曲线。可以看出,分层均衡构架在均衡效率上也有明显优势。均衡效率是指电池组中电池单体增加的能量之和与减少的能量之和的比值。从图11中可知,分层均衡方法最终平均SOC为85.01%,传统均衡方法最终得到的平均SOC值为83.61%。通过计算可得,分层均衡方法比传统方法的均衡效率高出12.61%。因此,分层主动均衡方式表现出了更好的均衡效果。
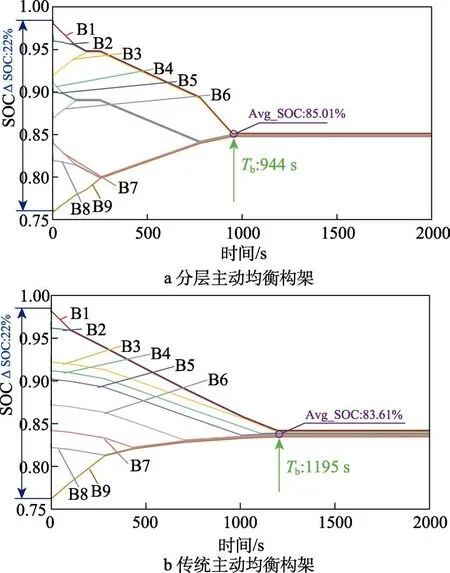
图11 电池组静置均衡对比 Fig.11 Battery pack static balance comparison: a) hierarchical equalization method; b) traditional equilibrium method
5 结论
文中提出了一种用于锂离子电池组均衡系统的分层主动均衡构架,该构架将电池分为多组,其中组间采用基于Buck-Boost均衡拓扑电路的主动均衡,组内采用基于反激式变压器的主动均衡。该构架有效地解决了相邻单体电池间均衡由于电池数量多而造成均衡速度慢的问题。同时组间采用以反激式变压器为核心的主动均衡方式,可以进行任意电池子组到电池组间的能量转移,具有更好的灵活性。该分层式均衡构架可减少反激式变压器的使用数量,在减少电路体积的同时,也降低了成本。通过在Matlab/Simulink中搭建分层主动均衡模型,并采用先组内均衡、后组间均衡的策略来验证该构架的性能。均衡前后电池组SOC的最大差值从22%降低至0.454%。与单一的相邻电池单体均衡方式相比,其均衡效果提升了43.04%,均衡时间缩短了24.4%,均衡效率提高了12.61%。因此,该分层主动均衡构架能够更好地应用于船舶或者汽车等具有大量锂离子电池串联的电池组均衡控制中。

