迭代的顺序加权中值图像滤波算法

黄文笔，谢翠萍，陈家益，石艳

（1.广东医科大学 教育技术与信息中心，广东 湛江 524023；2.广东医科大学 生物医学工程学院，广东 湛江 524023；3.岭南师范学院 信息工程学院，广东 湛江 524048）

0 引言

图像在成像、传输以及存储的过程中，经常受到脉冲噪声的干扰。脉冲噪声严重影响图像处理与分析的效果，比如图像分割与特征检测[1]。因此，对于图像处理与分析，去噪处理非常必要。脉冲噪声随机地将图像的部分像素改为图像灰度范围的最小值和最大值，另外，因为脉冲噪声的随机分布特性，去除脉冲噪声一般用非线性滤波算法，比如中值滤波算法[2]。加权中值滤波算法[3]以及中心加权中值滤波算法[4]对中值滤波算法进行改进，以加权系数区分邻域像素对中心像素的影响和相关性的大小。但是不加区分地去噪处理，是这些算法共同的缺陷，因为对信号像素进行处理，在一定程度上破坏了原有信息。于是，噪声检测技术应运而生，并应用于脉冲噪声的去除[5]中，比如开关中值滤波算法[6-7]。对噪声像素进行检测和定位，然后仅对噪声像素进行去噪处理，从而保护信号像素的原始信息。虽然开关中值滤波算法提升了去噪性能，但其缺乏鲁棒性，难以有效地应用于不同密度的噪声。于是，学者们提出了由局部噪声密度决定去噪邻域大小的自适应开关中值滤波算法[8-9]。文献[9]提出了一种自适应开关中值滤波（Different Applied Median Filter in Salt and Pepper Noise，DAMF）算法，简单地将灰度最值作为噪声判别的依据，在自适应大小的邻域中寻找信号像素，以对噪声像素的灰度进行中值统计估测。

作为对自适应开关中值滤波算法的一种改进，部分学者提出了自适应加权中值滤波算法[10-11]。文献[11]提出的自适应开关加权中值滤波框架（Adaptive Switching Weighted Median Filter Framework，ASWMF）自适应地用大小不同的邻域的加权中值作为噪声像素的灰度估测值。加权中值滤波固然能提升对噪声像素灰度估测的准确性，但是如何设定加权算子以准确反映像素之间的相关性，尚无固定标准。另外，在脉冲噪声的去除算法中，决策滤波算法[12-13]因其鲁棒的处理策略而备受关注。基于概率决策的块中值滤波（Probabilistic Decision Based Filter，PDBF）[13]算法最大的贡献就是提出了块中值的新概念，块中值是对传统排序中值的改进，以避免去噪处理过程中引入奇异灰度的可能性。

由于脉冲噪声分布的随机性及其灰度的离散性，一般地，均值滤波算法不用于脉冲噪声，但部分学者对均值滤波算法进行了改进，使得其对脉冲噪声的去除取得良好甚至比中值滤波算法更好的效果[14-16]，比如文献[16]提出了将均值滤波融合于中值滤波（Switching Median-Mean Filter，SMMF）的一种算法，取得了比一般的中值滤波算法更好的去噪效果。

现有的脉冲噪声滤波算法往往难以在去噪性能和计算速度上同时达到理想的效果，要么去噪性能差，要么计算复杂度较高，难以适用于实时的图像去噪处理。为了同时提升算法的效率和去噪性能，本文提出了一种迭代的顺序加权中值图像滤波（Iterative Sequentially Weighted Median Filter for Impulse Noise Removal，IWMF）算法。IWMF根据噪声与信号像素分布的局部统计特征进行噪声检测，以迭代的方式调用加权中值滤波算法对噪声像素的灰度进行估测。实验结果证明，IWMF同时具有快速计算的能力和优越的去噪性能。

1 脉冲噪声模型

被脉冲噪声污染的像素，其灰度取图像动态灰度范围的最小值和最大值。脉冲噪声满足随机分布，取最小灰度值和最大灰度值的概率密度均等。其分布整体上大致均匀，但是局部呈现明显的不均性。令P(x)为灰度x的概率密度，min和max分别为图像动态灰度范围的最小值和最大值，d为噪声的概率密度，脉冲噪声的概率密度函数为：

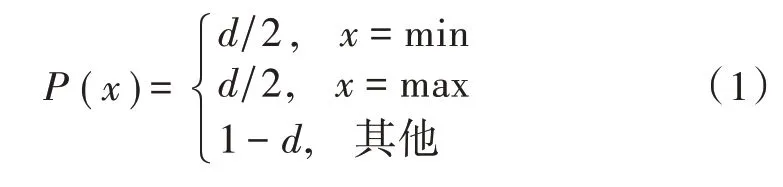
对于8位的灰度图像，脉冲噪声的灰度取0和255，密度d的取值区间为（0，1）。

2 IWMF算法

2.1 基于局部统计特征的检测

充分利用脉冲噪声的灰度最值特征，以灰度最值为依据，将灰度取最小值和最大值的像素归为噪声。明显地，这样会造成较高的误检率，因为最小灰度值与最大灰度值仍属于图像像素的灰度范围，图像中往往有一部分信号像素取灰度最值，特别是医学图形，这部分像素会被错误地识别为噪声。因此，在最值检测的基础上，提出基于局部统计特征的检测方法，进一步降低误检率。

图像的信号像素与其邻域像素具有相关性和灰度相似性，取灰度最值的信号像素也一样。比如，一个灰度取最小值的像素，其邻域像素往往多为最小值灰度的像素或灰度接近最小值的像素，它们之间具有承袭性。对于脉冲噪声，其并不具备以上特征，处于孤立的状态。根据以上分析，在基于灰度最值检测的基础上，进一步提出基于局部统计特征的噪声检测方法。

对于检测所用的邻域尺寸，太小会失去统计意义，太大会使得像素之间的相关性和灰度相似性较弱，不具备参考意义，因此，取5×5邻域。对每一个灰度取最值的像素，根据以下情况作出进一步的判断。

1）如果其5×5邻域内存在非最值的像素，且其与非最值像素中值的绝对差小于阈值T1，识别为信号，否则为噪声。

2）如果其5×5邻域内不存在非最值的像素，且与其灰度相同的像素占多数，识别为信号，否则为噪声。比如一个灰度为0的像素，如果其5×5邻域内灰度为0的像素数量n0>T2，将其识别为信号，否则为噪声。

2.2 迭代的加权中值去噪

对图像噪声的处理，以迭代的方式调用5×5邻域的加权中值滤波算法，对应的5×5加权算子W5如下所示：

W5中的系数是根据邻域中的信号像素与中心像素的空间距离，顺序地递减分布，以更加准确地体现邻域像素对中心像素的相关性及其相似性。值得注意的是，加权算子W5各位置上的系数对应于该位置上信号像素的加权系数，如果该位置上的像素为噪声，则其系数为0。

令f为噪声图像，f(i,j)为f中第i行第j列的像素，N(i,j)（5）为以f(i,j)为中心，大小为5×5的正方形邻域，median是中值运算函数，⊗表示复制操作符，其定义为：

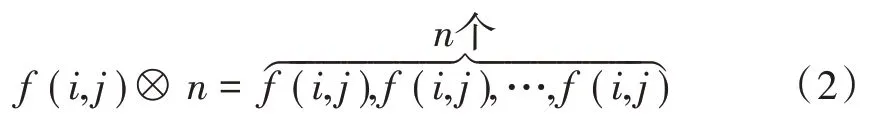
则5×5邻域的加权中值滤波算法（WMF5）定义为：

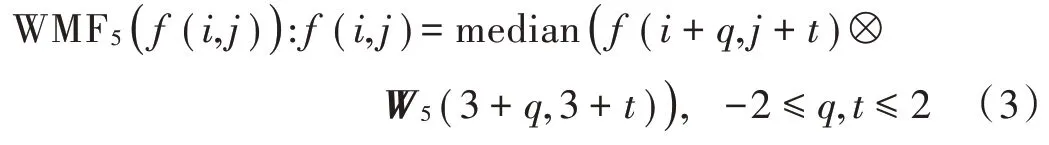
迭代的加权中值滤波处理的步骤如下：

1）对图像中每个噪声像素f(i,j)，如果N(i,j)（5）中存在信号像素，则调用WMF5（f(i,j)），并将f(i,j)标记为信号像素，否则，不作处理。

2）处理对象为上一次的滤波结果，处理与步骤1）相同。

3）重复执行步骤2）二次。

4）对图像中每个未处理的噪声像素f(i,j)，令f(i,j)=median（N(i,j)（5））。

即便噪声密度很高，对噪声图像经过迭代4遍的加权中值滤波，噪声像素所剩已经很少，最后的步骤4）对残余的噪声用其N(i,j)（5）的中值作为其灰度估测值。

2.3 IWMF算法的步骤

令R为噪声识别矩阵，和分别为N(i,j)（5）中灰度0，255和非最值灰度的数量；为了清晰表示，IWMF算法用伪代码表示如下。对于阈值T1和T2的最优取值，根据大量的实验和试错法，取T1=5和T2=20。

3 实验与结果分析

将数据集SET12中的Barbara和Hill，以及实际采集的医学图像Chest_XRay作为实验图像，其大小均为512×512，如图1所示。实验在PC机：IntelⓇCoreTMi5-4590 CPU at 3.30 GHz，8 GB RAM的实验平台Matlab R2019a中进行。将IWMF算法与现有文献中最近提出的部分算法应用于实验，分别是DAMF[9]、ASWMF[11]、PDBF[13]和SMMF[16]。基于去噪图像的视觉效果、峰值信噪比（Peak Signal to Noise Ratio，PSNR）、结构相似性（Structural Similarity，SSIM）[17]，以及算法的计算效率，将各算法进行比较。

图1 实验图像

3.1 视觉感知

对于含80%脉冲噪声的图像Barbara，IWMF算法与部分现有算法的处理结果如图2所示，每张图像下面括号中的两个数字分别为该图像对应的PSNR和SSIM值。为了视觉上的清晰比较，只显示图像放大后的一部分。

图2 各算法对含80%噪声的图像Barbara的去噪结果

细心观察各滤波图像可以发现：PDBF的去噪效果最差，模糊效果严重；ASWMF去噪不彻底，图像中留有噪声斑块；DAMF的去噪效果可以接受，但是边缘和细节部分出现明显的锯齿现象；SMMF的去噪效果相对较好。相对于现有算法，IWMF的去噪效果更好，其去噪图像的整体清晰度较高，边缘线条较柔和，彻底地去除了噪声，并且图像的细节和纹理结构保持得很好。各去噪图像对应的PSNR和SSIM值，进一步证实了IWMF算法相对于现有滤波算法在去噪性能上的优越性，与从去噪图像的视觉效果得出的结论一致。同时IWMF算法分别在PSRN和SSIM值上与其他算法的差距较大，意味着IWMF算法在纹理结构保持方面的优越性更加显著。

3.2 去噪图像的PSNR和SSIM

对于含不同密度脉冲噪声的图像Hill，各算法进行处理所得的PSNR和SSIM值如表1所示。

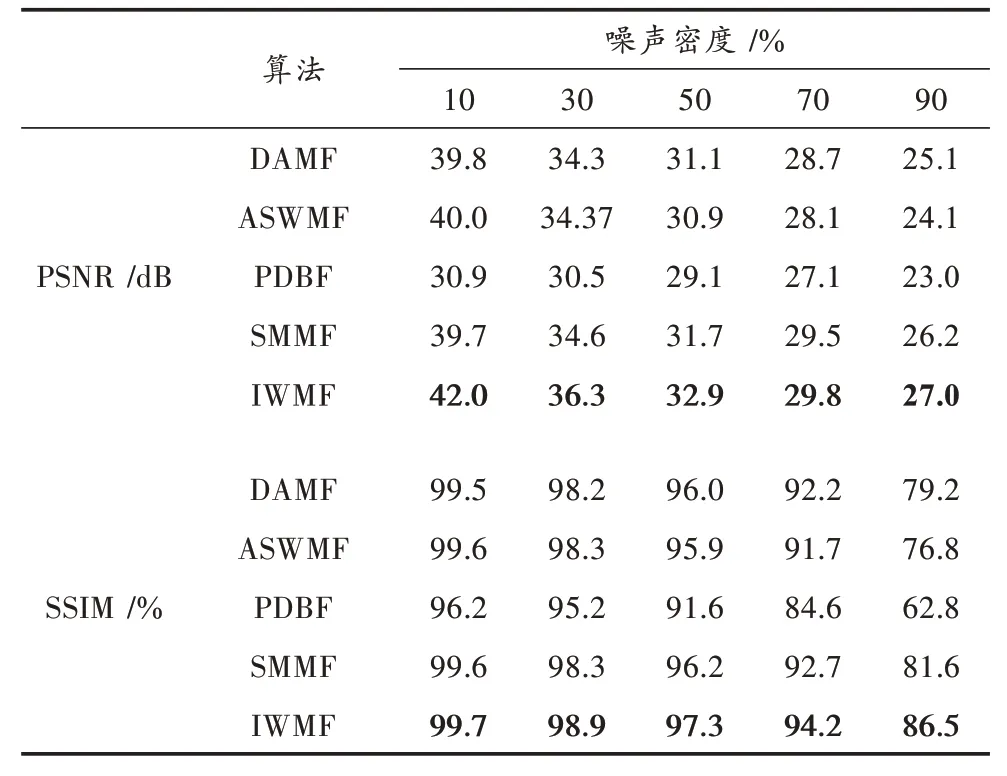
表1 各算法对含不同密度噪声的Hill去噪的PSNR和SSIM

表1中最优的指标值用黑体表示。根据表1中数据的走向以及对其进行的比较，可以得出如下4个重要结论：

1）PDBF的去噪性能较差，对细节和纹理结构的保持能力也较弱。

2）在噪声密度较低时，DAMF、ASWMF和SMMF的去除性能差别不大，处于可接受水平。但是在噪声密度较高时，DAMF和ASWMF在噪声去除和纹理结构保持方面的能力较差。

3）在不同密度噪声条件下，IWMF算法的去噪性能一致地优于现有的滤波算法，虽然在高噪声密度时，IWMF与SMMF的性能接近，但是始终与其他算法保持一定的差距。

4）SMMF，IWMF的纹理结构保持能力在噪声密度较高时愈加显著。

再以医学X光图像为实验图像，以验证IWMF算法的普适性。医学图像往往平滑区域较多，黑色和白色的区域较多，保持和恢复医学图像的细节特征对医学诊断和研究意义重大。对于各种密度噪声下的医学图像Chest_XRay，各算法的去噪结果如表2所示。

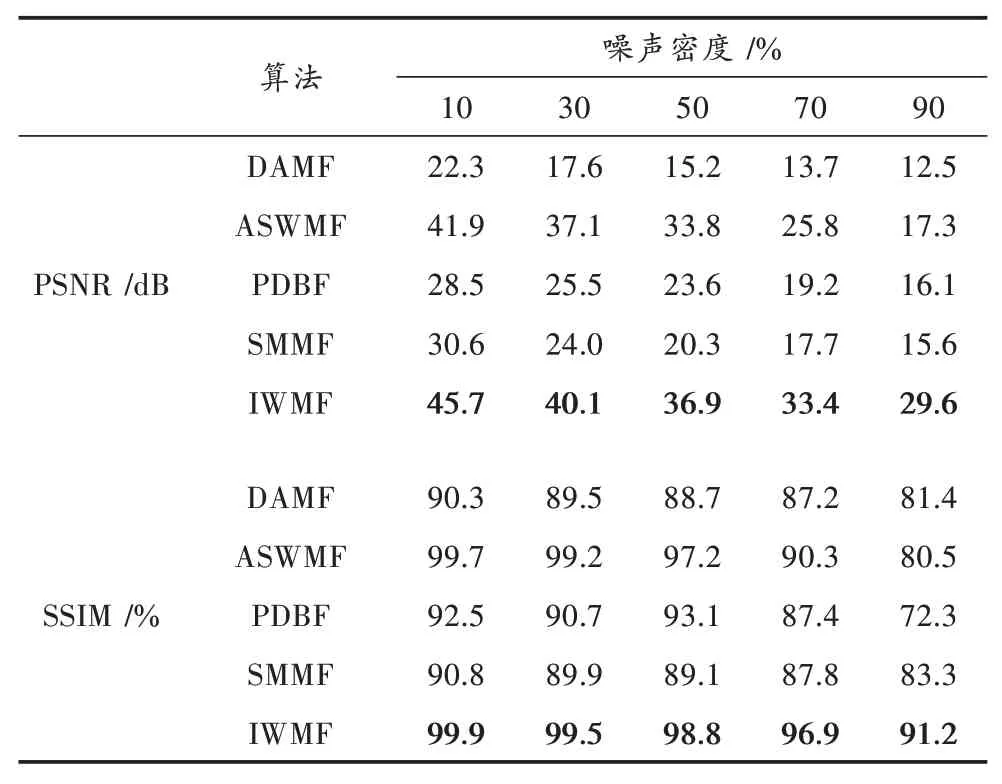
表2 各算法对含不同密度噪声的Chest_XRay去噪的PSNR和SSIM

根据表2中的数据可以得出如下3个结论：

1）对于每一噪声密度，各算法对应的数值差异悬殊，说明各算法的去噪性能差异悬殊。

2）IWMF的PSNR和SSIM值始终高于其他算法，与其他算法保持一定距离。

3）IWMF在高密度噪声时的优势比在低噪声密度时的优势更加显著。结果说明对于医学图像，IWMF在去噪的彻底性以及细节和纹理结构的保持上具有更好的能力，这完全得益于其基于局部统计特征能准确地检测噪声，以及迭代的加权中值滤波能够准确有效地估测噪声像素的灰度。

3.3 计算时间

用图像Barbara测试各算法的计算效率，实验结果如表3所示。其中，最优的指标值用黑体表示。表3的数据显示，ASWMF的计算速度最慢，PDBF和SMMF的计算速度中等；在噪声密度较低时，DAMF的计算速度最快，总体上，IWMF与DAMF的计算速度相差不大。

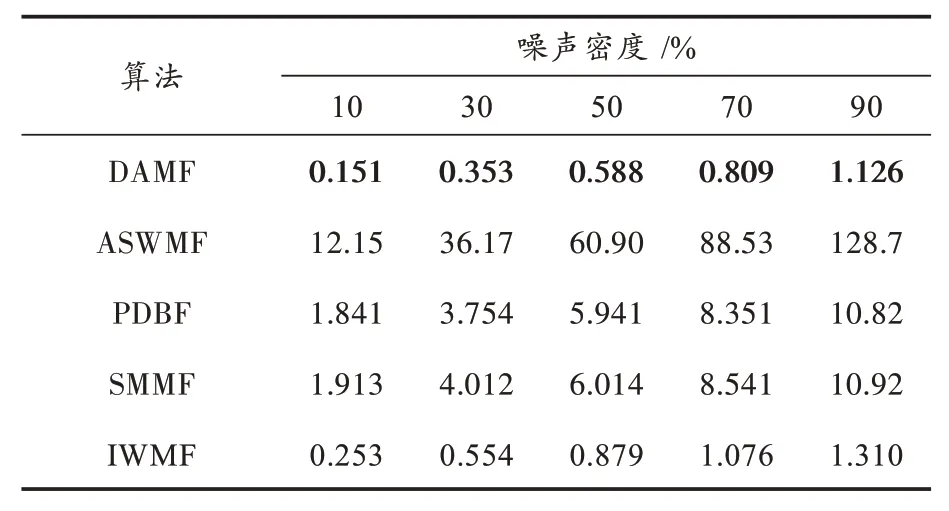
表3 各算法对Barbara去噪的计算时间 s

4 结语

为了克服现有滤波算法在去噪效果和计算复杂度上的瓶颈，提出了一种迭代的顺序加权中值图像滤波算法IWMF。IWMF基于噪声的灰度特征和信号像素的局部统计特征对噪声进行检测，迭代地调用加权中值滤波算法对噪声像素进行去噪处理。实验结果证明，IWMF算法在去噪性能上超越了现有的滤波算法，同时，快速的计算使其适用于实时的图像去噪处理。

注：本文通讯作者为陈家益。