非静止轨道卫星干扰与协调分析

戴成远，李鹏，方华，郭昊

（南京信息工程大学 电子与信息工程学院，江苏 南京 210044）

0 引言

近年来，随着卫星宽带业务的快速发展，每年发射入轨的卫星呈指数形式增长。传统静止轨道（Geosta-tionary Orbit，GSO）存在高时延、低吞吐量和传输损耗大等缺点，NGSO（Non-Geostationary Orbit）逐渐成为未来卫星研究领域的重点[1]。国外许多卫星通信公司都在致力于设计和研发NGSO卫星星座，欲利用NGSO卫星星座打造新的全球化卫星组网。NGSO卫星系统的不断增加，不仅会对同频段的GSO卫星系统、地面业务造成干扰，还会危及到其他同频段的NGSO卫星系统[2]。因此，卫星系统之间的干扰分析及协调是全球化卫星组网建设的重要支持。

目前国际电联针对卫星系统间的干扰分析方法，只有关于GSO卫星系统间的[3]，也形成了许多较为完善的干扰评价体系，例如INR（Interference Noise Ratio）、CIR（Carrier Interference Raitio）、EPFD（EquivalentPowerFlux-Density）、CDF（Cumulative Distribution Function）等相关时间或空间上数据指标。文献[4]提出了基于动态卫星星座的射频干扰分析方法；文献[5-6]分析了NGSO系统对GSO系统共线干扰时，通过功率控制的方法对干扰进行协调；文献[7-8]中提出了NGSO系统与GSO系统干扰时，通过设置角度禁区的方法，进行空间隔离。这些方法主要用于少数NGSO卫星与GSO卫星，分析I N，PFD等干扰物理量随时间和空间的变化。针对大规模NGSO卫星星座的特性，传统方法分析NGSO星座系统间干扰变得极其复杂。本文深入研究了NGSO卫星系统间干扰问题，采用卫星链路夹角的分析方法，给出全球范围内NGSO星座间干扰分析方案，并提出动态空间隔离角的协调方法，验证两NGSO星座系统间干扰协调的可行性及有效性。为了合理地对Ka频段资源进行开发使用，本文针对不同NGSO卫星网络在Ka频段的干扰问题进行理论分析，希望能为国家未来NGSO卫星星座频谱资源建设和协调提供理论参考。

本文主要贡献如下：提出了上行场景中NGSO卫星系统链路干扰模型，并给出干扰协调分析方案；对最坏情况下NGSO卫星系统之间的上行干扰进行分析，通过链路夹角的方法分析NGSO星座系统间的有害干扰；设置空间隔离角，仿真结果表明空间隔离角适用于协调NGSO卫星系统之间的有害干扰；提出全球范围内NGSO星座间干扰分析方法，并给出相关仿真验证。

1 干扰模型分析

为了分析NGSO系统之间的干扰特性，首先需要对每个卫星之间的链路进行建模。图1展示了场景为两卫星系统上行链路干扰，图中实线部分表示卫星通信链路，虚线部分表示干扰链路。例如，卫星1不仅可以接收到地面站1发射的有用信号，同时也会接收到地面站2发出的干扰信号。在卫星通信业务中，地面站发射天线主波束始终与卫星接收天线波束对齐，因此地面站2发射出的干扰信号对应的天线增益一般是由发射天线的旁瓣波束形成的。当卫星1接收天线接收到的地面站2发射天线旁瓣波束干扰达到一定程度时将会对卫星1通信造成影响。

图1 上行干扰场景示意图

NGSO卫星轨道相对于地球处于高速运动状态，从而导致NGSO卫星网络之间干扰与被干扰链路具有非固定且时变的特性。为了分析NGSO卫星系统间干扰场景，采取快照方式进行仿真[2]。对每个时间节点数据进行快照采样，统计整个仿真周期数据，得出I N累计变化数据。

2 干扰计算及协调方法

通常对两卫星星座系统进行干扰分析时，主要考虑新入卫星系统是否会对已有卫星系统通信造成干扰。在这种情况下，新入卫星星座产生的干扰是否在已有卫星通信业务能力承载范围内，当新入卫星星座与原有卫星星座使用相同频段时，应该在保证新入卫星通信质量的同时，确保原有卫星通信不受干扰。

图1为上行干扰场景示意图，假设卫星1和地面站1为被干扰的卫星系统，卫星2和地面站2为干扰卫星系统。当卫星1和卫星2同时出现在地面站可视范围内时，卫星1接收到地面站2发射的干扰载波，其卫星系统间干扰载波和系统噪声比为：

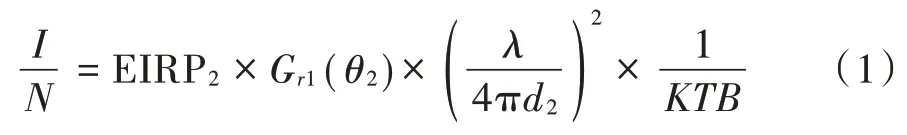
式中：EIRP2=Gt2(θ1)+Pt2，Pt2为地面站2的发射功率，Gt2(θ1)为地面站2发射天线偏离主轴θ1度角的发射天线增益；Gr1(θ2)为卫星1接收天线偏离主轴θ2度角的接收天线增益；d2为地面站2发射出的干扰链路距离；K为玻尔兹曼常数（1.38×10-23J/K）；T为卫星接收机的系统噪声温度，单位为K；B为转发器信道带宽，单位为Hz。

根据《无线电规则》附录[3]，当干扰卫星系统发出的干扰信号对卫星通信链路引起的噪声温度增量不超过6%时，则视为无害干扰，则不需要进行相关协调。

式中：ΔT为干扰链路对卫星通信系统造成的等效噪声增量；T为卫星接收机的系统噪声温度。

转化为相应的干扰噪声比为：

因此，I0N0=-12.2 dB被视为卫星通信链路能承受的干扰阈值。

在分析卫星通信上行链路干扰时，不仅需要对卫星系统间干扰信号强度进行分析，而且当卫星接收到的干扰信号超过阈值时，如何对干扰信号协调是未来研究的重点。本文列出以下几种协调方案：

1）功率控制。当卫星接收到的干扰达到阈值时，可选择增大卫星地面站发射功率或者降低干扰卫星地面站的发射功率。增大卫星地面站发射功率时不仅会相应提高链路性能，也可能会干扰同频段的其他卫星链路；而降低干扰卫星地面站发射功率，则会一定程度影响到干扰卫星系统的正常通信业务。

2）关闭传输。对某一固定位置地面站，当NGSO卫星接收到的干扰达到阈值时，将其中一卫星系统波束关闭传输，避免卫星系统间共线干扰，但也间接导致覆盖区信号的中断。

3）空间隔离角。在地面站上行波束产生的干扰达到干扰阈值时，自动切换到可视范围内的其他卫星组成链路，针对NGSO多星特性，这种方法也更适合NGSO卫星系统间的干扰协调。

本文通过NGSO卫星系统间链路夹角分析卫星信号INR，选择空间隔离角作为协调干扰的方法，分析空间隔离角在NGSO卫星系统间的可用性。

3 空间隔离角分析

在两卫星系统地面站重合的极端情况下，由于卫星轨道高度的不同，当两卫星与地面站处于一条直线位置时，则被视为共线干扰。共线干扰严重影响到正常的卫星通信业务，因此在即将达到共线干扰的同时，需进行相应的干扰协调，而对于两卫星地面站重合的极端情况也必然适用于两卫星地面站不同址的其他情况。如图2所示，当两卫星系统地面站同址时，链路夹角随着卫星空间位置的变化而变化。

图2 空间隔离角

假设卫星1的空间位置坐标矢量为S1(t)=(xa(t),ya(t),za(t))，卫星2的空间位置坐标矢量为S2(t)=(xb(t),yb(t),zb(t))，地面站的空间位置坐标矢量为E(t)=(x(t),y(t),z(t))。θ为两卫星链路夹角，β为卫星通信系统的阈值夹角，也被称为空间隔离角。

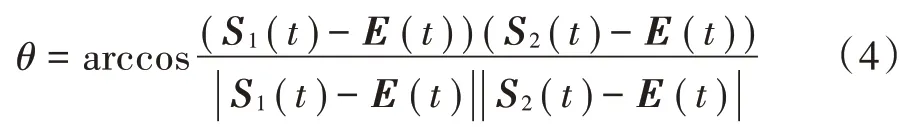
当θ≤β时，表示卫星1接收的干扰信号超过干扰阈值，被视为有害干扰。

为了分析NGSO卫星星座系统间干扰，对于某固定位置的地面站，设置地面站最低可视仰角，可见星座1的卫星数目为m，星座2的卫星数目为n，其组成的链路干扰组合为m×n，计算整个仿真周期内每个采样间隔地面站可见星座1与星座2所有卫星链路之间的夹角θi，统计整个样本数据中有害干扰（θi≤β）的个数t，其星座系统间有害干扰CDF为：

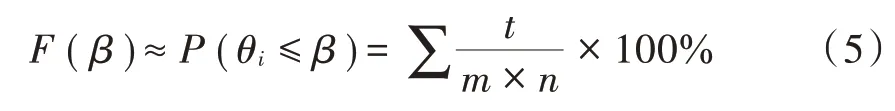
F值越大，表明星座系统受到的干扰越严重，根据《无线电规则》[3]干扰保护标准，制定合适的干扰协调方案，以保证卫星通信业务的质量。通过遍历全球不同位置的地面站，得出全球范围内不同NGSO卫星星座间有害干扰概率分布。

4 干扰仿真分析

模 拟NGSO星座间干扰仿真，以O3b星座[9-10]与SpaceX星座[11]为例，使用STK与Matlab软件进行干扰仿真计算，分析SpaceX卫星对O3b卫星的上行干扰，仿真验证了干扰分析与协调的可行性。

4.1 仿真参数设置

卫星星座干扰分析过程中，从提交给FCC（Federal Communications Commission）的每个申请中详细列出的链路预算示例中提取O3b卫星和SpaceX卫星的参数值。其中，O3b卫星轨道高度为8 062 km，16颗在轨卫星均匀分布在轨道倾角为0.1°的圆轨道，主要用于Ka/Ku频段通信；SpaceX卫星总数为1 600颗，轨道高度为1 150 km，轨道面数为32个，均匀分布在轨道倾角为53°的圆轨道。其余链路参数取值如表1所示。

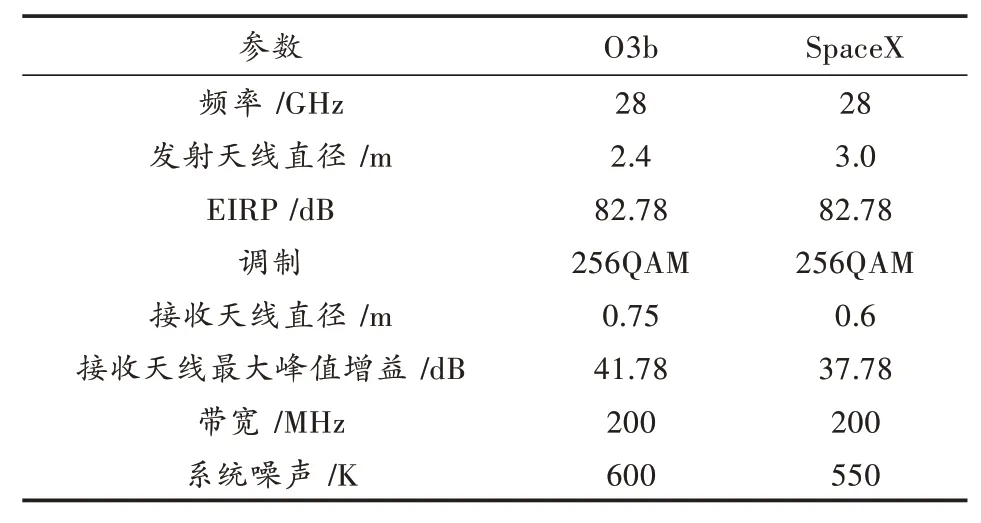
表1 Ka频段两卫星系统链路参数

假设两卫星系统地面站重合，位于32.158°E，0°N的赤道位置。考虑到两卫星星下点轨迹时变特性，为保证仿真数据的准确性，本文将设置仿真时长为3 d，采样间隔为10 s。

4.2 卫星系统间干扰分析

由于NGSO卫星系统的运动特性，轨道相对地面站位置是时变的，在满足星座系统地面站最低可视仰角，并非每个运行周期都可以建立起通信链路。SpaceX卫星系统对O3b卫星系统造成干扰的条件是O3b卫星接收到来自地面站发射信号的同时，接收到SpaceX卫星系统地面站发射的干扰信号。

在3 d仿真周期内，共出现6次干扰，平均干扰时长约为14.77 min，如图3所示。6次干扰信号的角度变化率充分体现出NGSO卫星轨道的快速时变特性，其中第3次由于出现共线干扰，造成角度变化率偏大。

图3 链路夹角变化率

地面站的参考天线方向图根据ITU-RS.465-5建议书[12]，由式（1）计算，代入相关链路参数，SpaceX卫星发射的干扰信号I N随链路夹角的变化如图4所示。

图4 I N随链路夹角的变化图

参考式（3）中GSO卫星系统干扰协调标准，由图4可知，两卫星链路夹角阈值为4.707°，当链路夹角在0°~4.707°时，O3b卫星接收到的干扰信号超过干扰保护标准视为有害干扰，应选择相应的协调措施；反之，则不需要进行协调。

在NGSO卫星系统间上行链路干扰场景中，通过未加空间隔离角与设置不同空间隔离角进行对比，目的是验证设置空间隔离角对干扰信号的影响。图5为无空间隔离角和空间隔离角为5°，7°，9°时I N的变化对比。结果显示空间隔离角在一定程度上协调了上行干扰，而且随着空间隔离角的增大，干扰协调效果有很大的提升，符合正常通信链路余量需求，证实空间隔离角对NGSO卫星干扰协调是有效的。

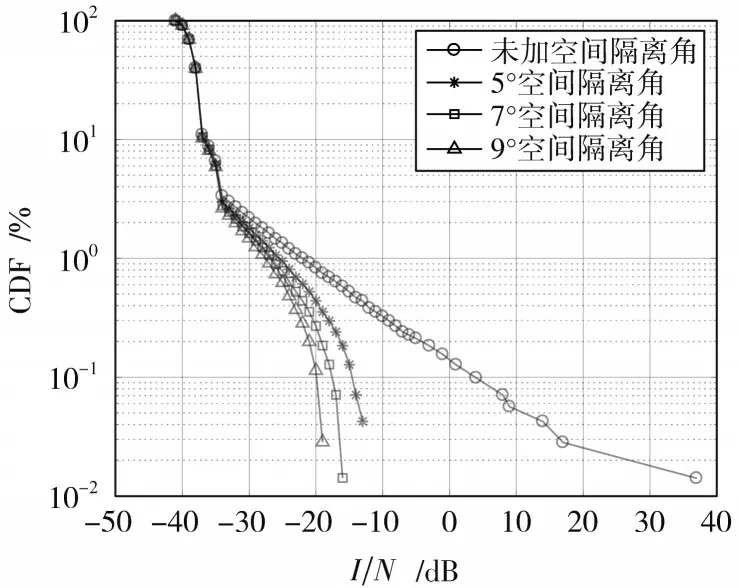
图5 I N的累积分布

在某一固定位置地面站，不同时刻可视O3b星座和SpaceX星座卫星数目也是变化的，根据式（4），式（5）计算，得出SpaceX星座在固定地面站位置对O3b星座链路夹角的概率分布，如图6所示。

图6 星座系统间干扰概率

图6中，星座系统间干扰概率是随时间变化的，γ1表示固定位置地面站，卫星星座2对卫星星座1有害卫星数目与可见卫星数目之比；γ2表示卫星星座1与卫星星座2组成的有害链路夹角与总的夹角之比。仿真结果表明，不同时间节点干扰概率是不同的，在某些时间并未产生有害干扰。本文采用γ2进行有害干扰概率统计，加入星座系统组合特性，组合数据量加大，统计概率值降低。因此计算星座系统间干扰概率需统计大量数据进行均值计算，进一步减少计算误差。

如图7所示，在地面站0° N位置处O3b卫星星座与SpaceX卫星星座链路夹角为CDF，其对应最大I N值为37.58 dB。根据ITU-RS.1528的卫星系统干扰保护标准，卫星接收到的干扰值I N大于-12.2 dB的持续时间[13]不超过仿真周期的0.1%。由仿真结果显示，有害干扰累积概率为0.31%，已超过了卫星干扰保护标准，需要进行相关干扰协调。

图7 星座间链路夹角累积分布

根据资料显示，SpaceX星座是包含数千颗卫星的大规模星座，可以实现对地的多重覆盖。考虑到树木、建筑物等造成的信号阻塞，若按地面最低可视仰角为10°计算，设置空间隔离角。针对NGSO多星特性，在SpaceX地面站上行波束产生的干扰达到阈值时，自动与可视范围内的其他卫星组成链路，避免对O3b卫星通信造成有害干扰。

分析SpaceX星座与O3b星座间的干扰，遍历全球范围内不同位置地面站，得到O3b星座接收到干扰的CDF如图8所示。有害概率主要分布在中低纬度地区，随着纬度的升高概率值增大，在中纬度地区概率最高，干扰概率分布累积值为1.822%，在南北纬54°~90°之间，O3b卫星星座无法与地面站建立链路，因此不会产生有害干扰信号。

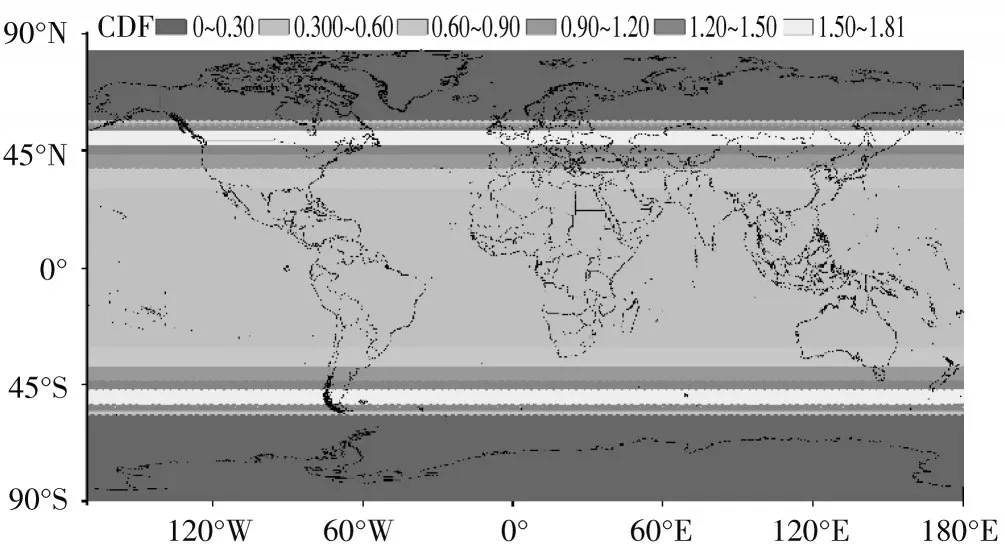
图8 全球范围内有害干扰概率分布

5 结语

本文对Ka频段NGSO卫星星座系统间上行干扰进行分析。采用传统GSO卫星干扰保护标准，定义了NGSO星座间有害干扰概率和空间隔离角协调干扰指标。虽然NGSO单颗卫星间干扰概率极低，但由于NGSO卫星数目众多且具有相对时变特性，造成星座系统间有害干扰加大，干扰分析难度也变得极其复杂。空间隔离角是否会影响到正常卫星通信业务，是否适用于其他干扰场景，还需进一步的验证。