一个几何问题的代数思考

马纪英 贾慧羡 姜文鹏

摘要：文章以一道几何问题的三种解题思路为依托，融合正弦定理、塞瓦定理、三角函数、导数应用等几何、代数、微积分内容为一体，反对解题思路的割裂，体现数学的关联性，为数学的综合应用提供思路。

关键词：正弦定理;导数应用;塞瓦定理;融合

中图分类号：O13文献标识码：A

Algebraicthinkingofageometricproblem

MaJiyingJiaHuixianJiangWenpeng

ShijiazhuangPostsandTelecommunicationsTechnicalCollegeHebeiShijiazhuang050021

Abstract：Basedonthreesolutionstoageometricproblem，thispaperintegratesthegeometry，algebraandcalculuscontentssuchassinetheorem，Ceva'sTheorem，trigonometricfunctionandderivativeapplication，opposestheseparationofsolutions，embodiestherelevanceofmathematics，andprovidesideasforthecomprehensiveapplicationofmathematics.

Keywords：sinetheorem;derivativeapplication;Ceva'sTheorem;fusion

在我們的学习过程中，无论是中学生还是大学生，一般几何相对来说是一个稍显封闭的学科。在初高中的平面几何、立体几何中，几何问题是采用独特的几何证明方法或计算方法自行内部解决的;在高中和大学的平面解析几何和立体解析几何中，几何问题开始与函数进行了结合，开始使用函数的形式或向量运算的形式表示直线、平面以及他们的关系或者一些具体的运算，更进一步是正弦定理、余弦定理或者行列式的表示和引入，总体来说，几何问题在我们触及的学习过程中与强大的微积分工具结合不是很深入。

文章引入的是一道直观的几何问题，但又不是纯粹的几何问题，也不是单纯的解析几何问题，解题过程中不同程度地涉及代数计算、函数推导、三角公式、导数应用等多方面内容，适用于多个数学分支的综合应用。

1问题描述

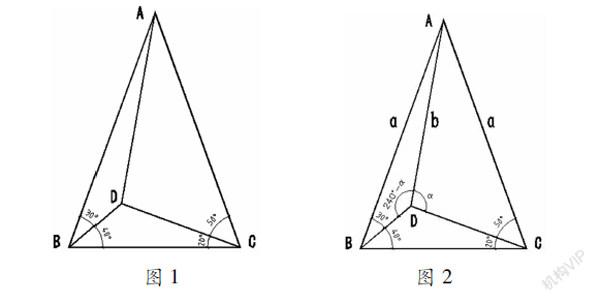
如图1，三角形ΔABC，D为ΔABC内一点，连接DA、DB、DC，已知∠DBA=30°、∠DBC=40°、∠DCA=50°、∠DCB=20°。问∠DAC=？

2解法一（正弦定理+解析计算）

正弦定理是三角学的一个基本定理，在三角形的代数运算中具有非常广泛的应用，它的描述是：在任意一个平面三角形中，各角的正弦值和它所对应的边的比值是相等的，并且它的倒数等于外接圆的直径。也就是：

asinA=bsinB=csinC=2r=d

正弦定理最早可以追溯到13世纪阿拉伯数学家、天文学家纳绥尔丁和15世纪德国数学家雷格蒙塔努斯的“同径法”，也就是将三角形内角的正弦作为同半径圆的正弦线，再使用三角形的相似性质计算出两个正弦值之比和角的对边之比相等。17到18世纪，我国数学家、天文学家梅文鼎和英国数学家辛普森又分别独立对“同径法”进行了简化。19世纪，英国数学家伍德豪斯把半径选取为1，把正弦线发展为比值的三角函数，最后得到了今天普遍采用的正弦定理表达式。

如图2，令∠ADC=α，则∠ADB=360°-α-（180°-40°-20°）=240°-α，并且α∈（90°，130°）;又有∠ABC=∠ACB=70°，则ΔABC为等腰三角形，设AB=AC=a，AD=b。

在ΔACD内使用正弦定理，有：

asinα=bsin50°（1）

在ΔABD内使用正弦定理，有：

asin（240°-α）=bsin30°（2）

由（2）式得：

b=12asin（240°-α）

代入（1）式有：

asinα=12asin（240°-α）sin50°

整理有：

12sinα=sin（240°-α）sin50°（3）

=sin240°cosαsin50°-cos240°sinαsin50°

=-32cosαsin50°+12sinαsin50°

于是：

（12-12sin50°）sinα=-32sin50°cosα

tanα=-32sin50°12-12sin50°

计算，由：

sin50°≈0.766

可得：

tanα≈-5.6697

即：

α≈-79.99727°+180°k

k为整数。

从而α≈100.00273°，可以估算为α=100°。

代入（3）式中验证：

右边=sin（240°-100°）sin50°

=12（cos90°-cos190°）=-12cos190°