圆盘塔倒塌的动力学分析

朱世栋,黎秋航,侯吉旋,陈 乾

(东南大学 a.物理学院;b.交通学院，江苏 南京 211189)

2020年国际青年物理学家锦标赛(IYPT)的第14赛题为“下落的塔(Falling tower)”：相同的圆盘，一个叠在另一个上面，形成独立的塔. 当突然施加水平力移除塔底部的圆盘时，塔身的其余部分会掉落到底面上，并且依然保持直立状态. 研究该现象并确定允许塔保持静止直立的条件. 这是经典的理论力学问题，可以引申到建筑物稳定性等实际问题. 针对圆盘堆叠的模型，王涵等[1]提出了用倒塌概率判定塔稳定性的思路，并通过实验分析了相关参量的影响. 但研究因素较少. 舒幼生[2]对此类刚体堆叠问题做了理论研究，得出了底部物体抽出过程中塔的其他部分不会有相对运动的结论，并提出了不同条件下存在多种运动状态的可能性.

本文的理论部分分为基础理论与特殊情况2部分，将对圆盘的整个运动过程进行深入分析，得到塔是否倒塌的判别条件，并通过参量分析得到影响塔稳定性的因素. 实验部分将对理论中得到的结论进行佐证.

1 基础理论模型及求解

1.1 是否倒塌的判别条件

通过几个简单的预实验发现，移除最下方圆盘会导致上方圆盘的错开，错开的距离决定了塔是否倒塌. 通过求解落地后圆盘间的错开距离可以得到塔是否倒塌的判别条件. 设圆盘数为N，单个质量为m，半径为r，厚度为h.地面摩擦系数设为μ0，圆盘间粗糙程度相同，具有相同的摩擦系数μ1. 底部圆盘受到突然的水平力后获得初速度v0. 为方便描述，将圆盘从下到上编号1～N，如图1所示.

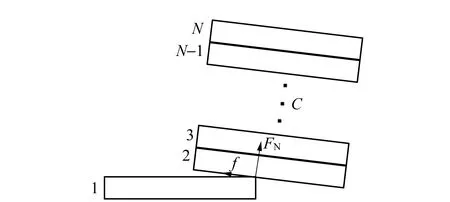
图1 圆盘塔的质心旋转

以下均假设圆盘落地前近似水平. 设圆盘质量分布均匀，则圆盘1和2错开x时，上方圆盘会开始翻覆. 圆盘1与2只有唯一接触点，所有的摩擦力与支持力都作用在这个点上，且

FN=(N-1)mg,f=μ1(N-1)mg.

(1)

取过质心且垂直于底部圆盘速度方向的转轴，由角动量定理[3]：

(2)

其中Ic为上方圆盘塔的转动惯量，且

(3)

当底部圆盘初速度很大(v02≫gr)时，可近似为匀速抽出，即

x=v0t.

(4)

将式(4)代入式(2)即可得到关于t的微分方程为

(5)

从0积分到r/v，即可以得到落地时圆盘塔的角速度为

(6)

如图2所示，刚落地的瞬间，各圆盘还未发生相对运动. 且各圆盘速度为质心速度与相对质心速度的叠加，由于绕质心旋转，各圆盘速度并不相同，因而错开. 相邻两圆盘间速度差恒定：

Δv=ω1h,

(7)

设圆盘2～N的质心速度为v，可得圆盘2～N的速度分别为

(8)

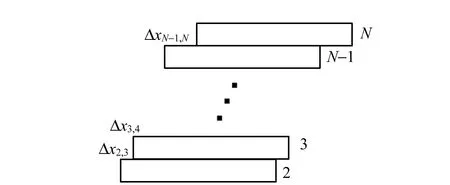
图2 圆盘的错开

只有最下方圆盘2在减速，加速度a2可由牛顿第二定律算出：

μ0(N-1)mg+μ1(N-2)mg=ma2.

(9)

上方所有圆盘在以相同的加速度a加速，以上数第k个圆盘为例，由牛顿第二定律有

μ1kmg-μ1(k-1)mg=ma,

整理得

a=μ1g.

(10)

因此，圆盘2将减速，圆盘3将加速，最终两者共速，形成整体(这里不考虑两者共速后仍有相对运动的情况)，有

v2-a2t1=v3+at1,

(11)

最终圆盘2与圆盘3错开的距离可由运动学公式算出：

(12)

联立式(8)～(11)，解得：

(13)

之后将圆盘2和3视为整体，这个整体在减速，上方圆盘在以相同的加速度加速. 重复式(8)～(11)的过程，可得圆盘3与圆盘4的错开距离. 类似地，可得所有圆盘的错开距离为

(14)

得到了错开距离分布，可以算出各质心的坐标. 以第k-1个圆盘的右边缘为原点，上方第k～N个圆盘的质心坐标为

xck=[m(-r+Δxk-1,k)+

m(-r+Δxk-1,k+Δxk,k+1)+…+

m(-r+Δxk-1,k+…+ΔxN-1,N)]·

[(N-K+1)m]-1.

(15)

联立式(14)和式(15)，化简得：

(16)

故圆盘塔不倒塌的条件是，k取任何值，xck≤0，即：当k在3～N中变化时，max{xck}≤0. 令d为此最大值：

(17)

d即为表征圆盘塔是否倒塌的判别条件：当d≤0时，圆盘塔不倒塌；d>0时，圆盘塔倒塌.

1.2 影响圆盘塔稳定性的因素

通过改变各参量，观察d的变化趋势，即可知道此参量对圆盘稳定性的影响. 以下逐次探究圆盘数量N、初速度v0、半径r与厚度h、摩擦系数μ0和μ1的影响.

初始条件：r=0.04 m,h=0.02 m,v0=0.7 m/s,g=9.8 m/s2,μ0=0.2,μ1=0.5.

如图3所示，固定其他参量的值，改变圆盘数量N.当圆盘数量增加时，d值增大，说明塔逐渐不稳定. 故圆盘个数越多，塔越容易倒塌.

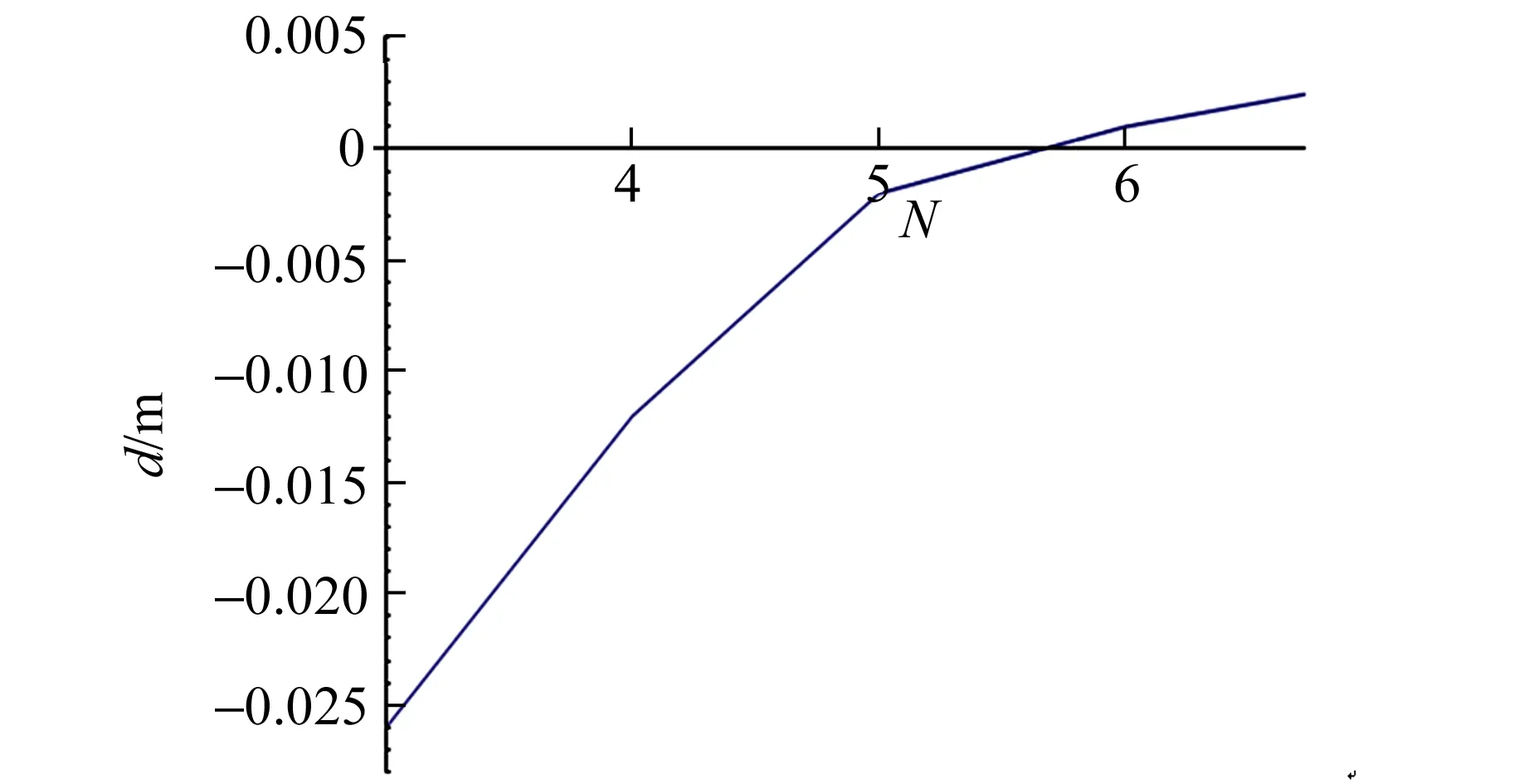
图3 圆盘数量对稳定性的影响

如图4所示，固定其他参量值，改变v0. 当v0增加时，d值减小，说明塔越来越稳定. 故底部圆盘v0越大，塔越不容易倒塌.

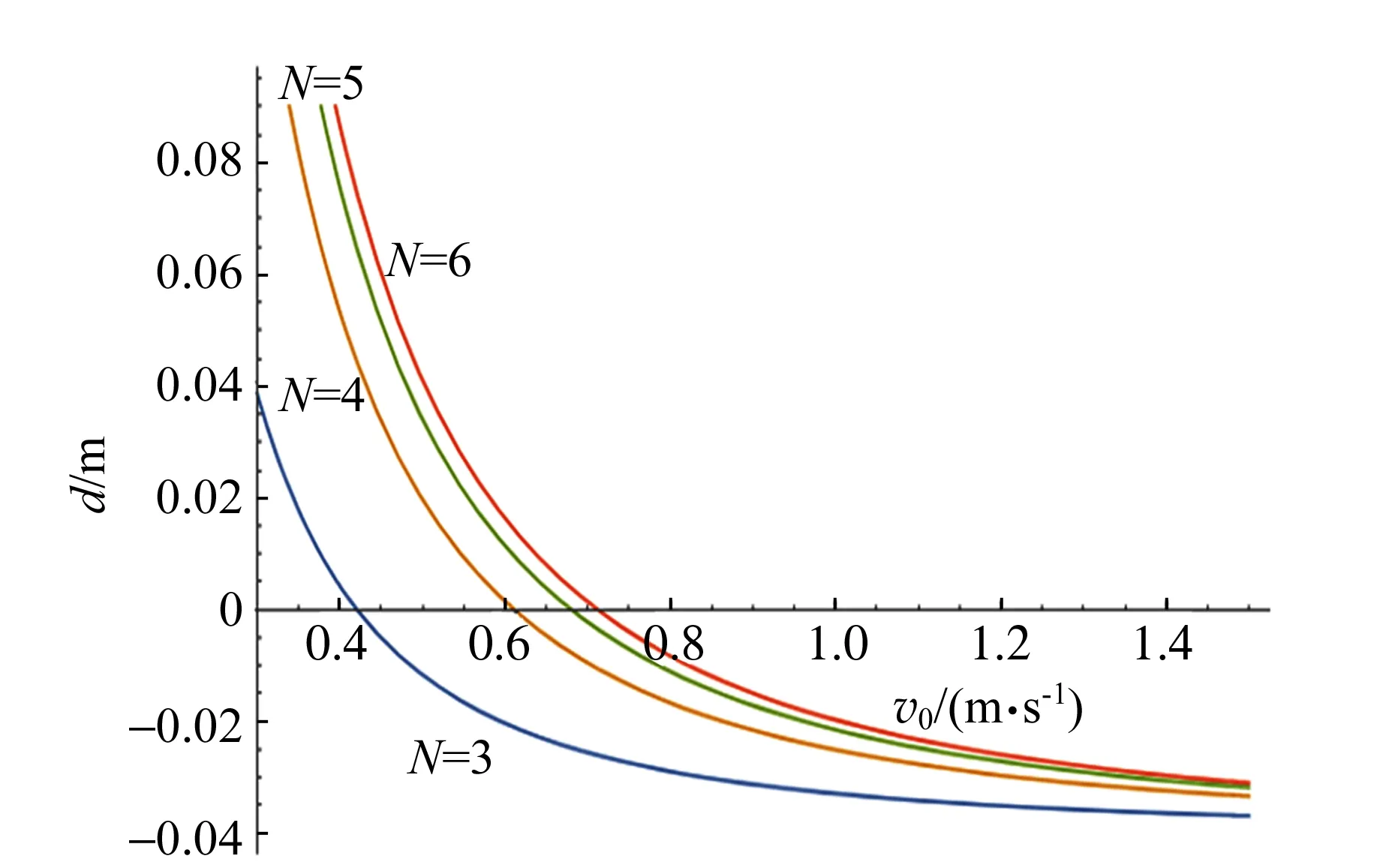
图4 底部圆盘初速度对稳定性的影响

如图5所示，圆盘半径与厚度对稳定性的影响耦合性较强，且当圆盘尺寸较小时，塔更稳定；圆盘尺寸较大时，塔更容易倒塌.

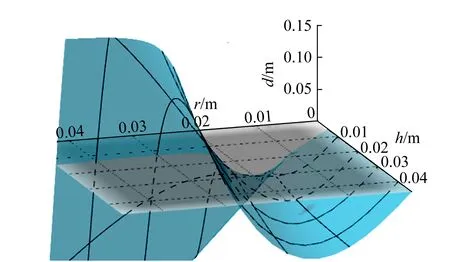
图5 圆盘尺寸对稳定性的影响

如图6所示，摩擦对稳定性的影响耦合性不强，且地面摩擦越大、圆盘间摩擦越小，d值越小，圆盘塔越稳定.

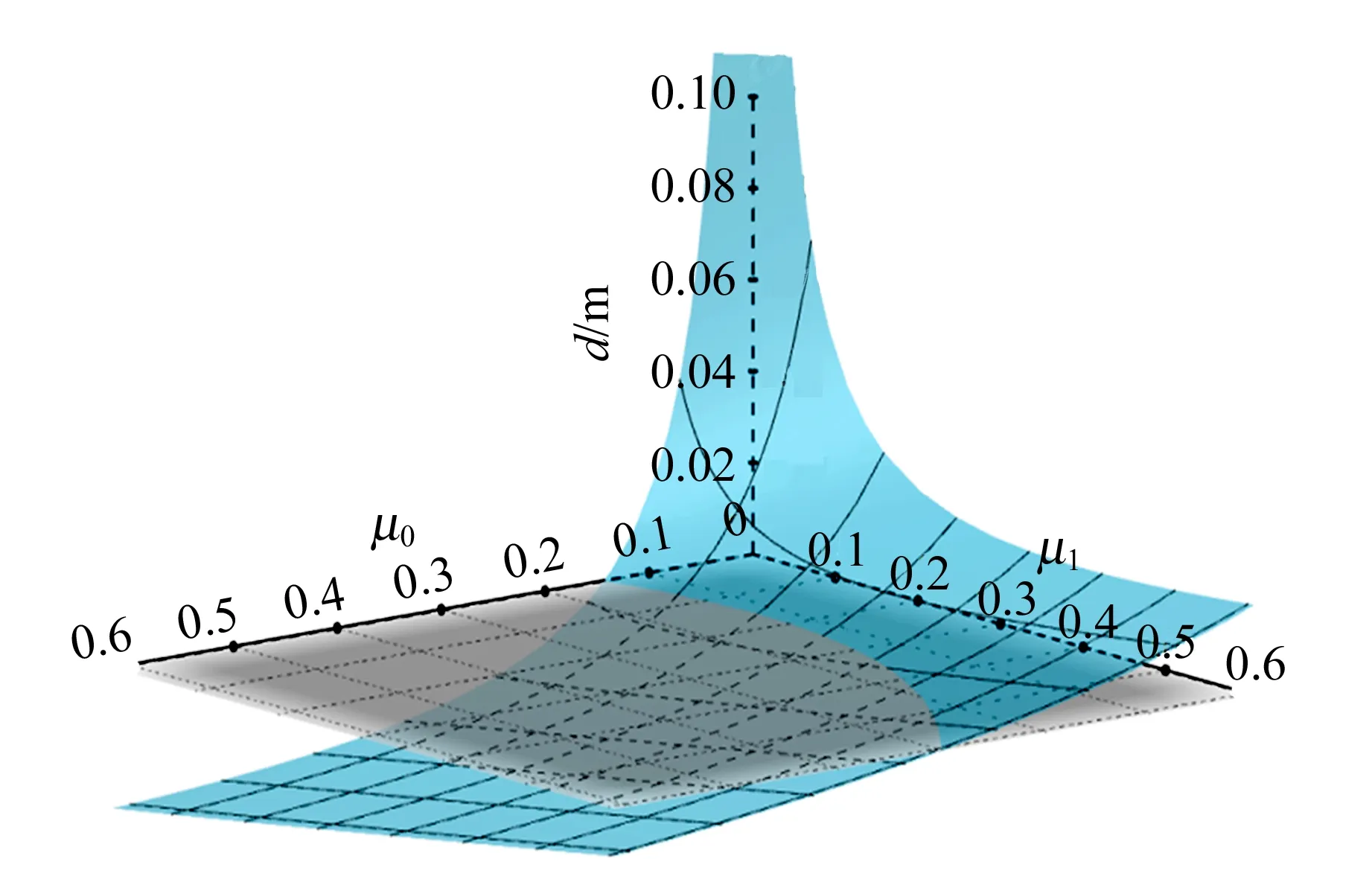
图6 摩擦对稳定性的影响

2 特殊情况分析

2.1 “溜坡”

“溜坡”是指圆盘落地后翻回水平过程中上方圆盘的侧滑. 由实验可知“溜坡”发生的条件为：

1)圆盘厚度较大；

2)地面摩擦较大；

3)圆盘间摩擦较小.

下面用简单模型计算“溜坡”产生的错开距离.

模型假设：

1)N=3，即落地时只有2个圆盘；

2)地面摩擦无穷大，即下方圆盘做定轴转动；

3)圆盘间摩擦为0.

如图7所示，设圆盘错开的距离为x，与地面的夹角为θ.取下方圆盘为参考系，引入惯性离心力、切向惯性力和科里奥利力，在图7中标出方向. 设两圆盘间作用力为FN，则FN作用线过上方圆盘质心(保证上方圆盘力矩平衡)；再设几何参量φ，已在图中标出.

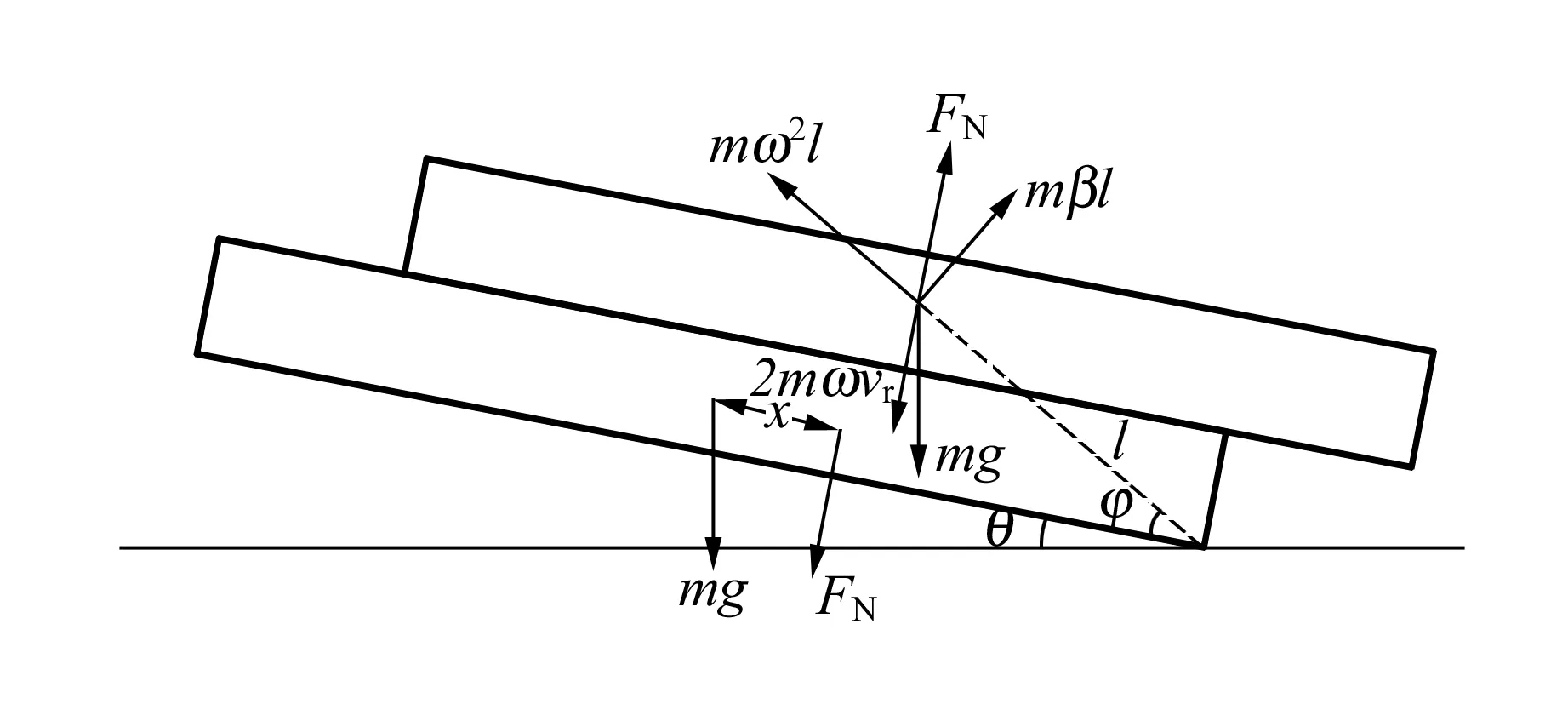
图7 “溜坡”现象分析图

对上方圆盘进行受力分析，垂直盘面方向受力平衡：

2mωvr+mgcosθ=mβlcosφ+mω2lsinφ+FN,

(18)

上方圆盘在平行盘面方向做变加速直线运动，由牛顿第二定律得

mgsinθ+mβlsinφ-mω2lcosφ=mar.

(19)

选取地面为参考系，对下方圆盘进行分析. 取与地面接触点为转轴，由角动量定理[1]得

mgcosθ·r+FN(r-x)=Iβ,

(20)

其中圆盘对转轴的转动惯量I为

(21)

最后通过几何关系关联φ，l和x，可得cosφ和sinφ为

(22)

联立式(19)～(22)，即可得到关于t的微分方程组，从而求解出x(t)与θ(t)，如图8所示.

若要求圆盘翻回水平时错开的距离，即求θ=0时x的值. 如图8所示，可以看出错开距离x≈0.03 m，而圆盘半径只有0.04 m，故“溜坡”现象导致的额外错开距离实际有重要影响.

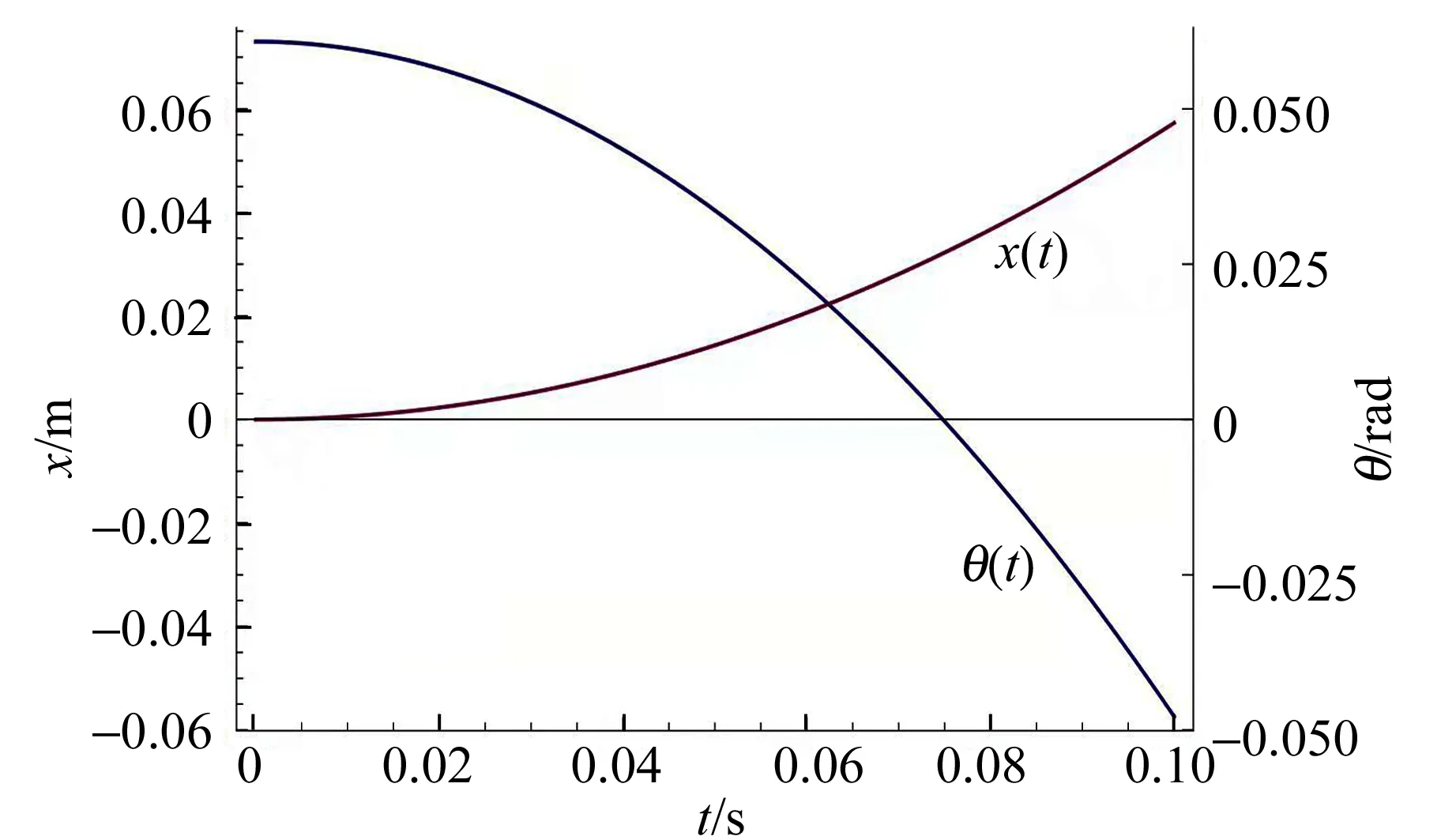
图8 x(t)和θ(t)的求解曲线

2.2 “破碎”

“破碎”现象指抽出最下方圆盘，上方圆盘在空中彼此分离的现象. “破碎”现象一般发生在圆盘间摩擦较大的情况. 下面用简单的模型分析发生“破碎”现象的原因.

模型假设：

1)N=3，即空中只有2个圆盘；

2)最下方圆盘匀速抽出，即在惯性系对空中两圆盘进行分析；

3)上方两圆盘在“破碎”前无相对运动；

4)两圆盘间压力为0时发生“破碎”.

如图9所示，设圆盘1对2的支持力为FN，摩擦力为μ1FN. 设圆盘转角为θ，圆盘2和3的质心C距离支点的水平距离为x，竖直距离为y.

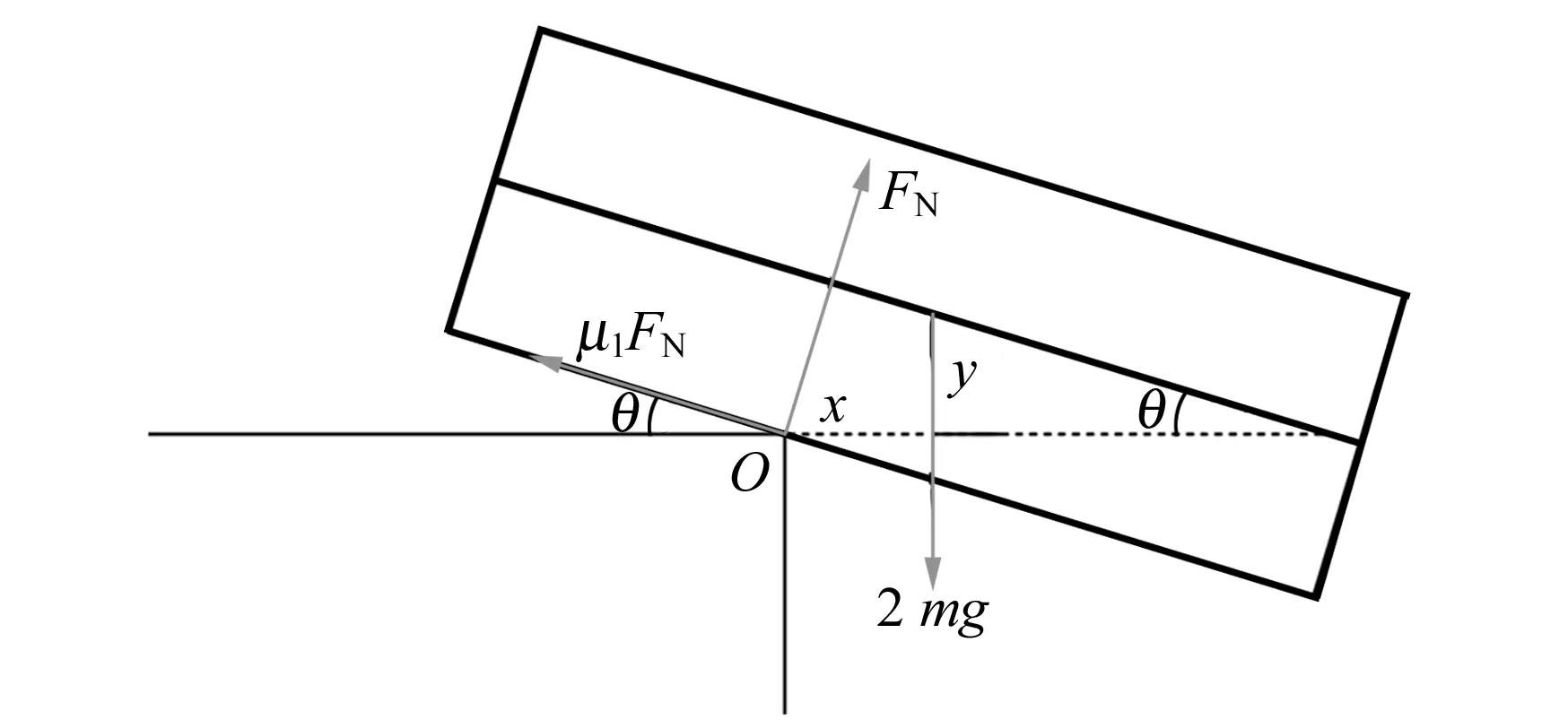
图9 “破碎”现象分析图(整体)

对整体进行受力分析，由质心运动定理[3]得

(23)

由整体的角动量定理可得

(24)

其中上方两圆盘对质心的转动惯量I为

(25)

并有几何关系：

(26)

对最上方圆盘做隔离分析. 设其所受摩擦力为f，支持为F，等效作用点为A点(位置无需讨论)，如图10所示.

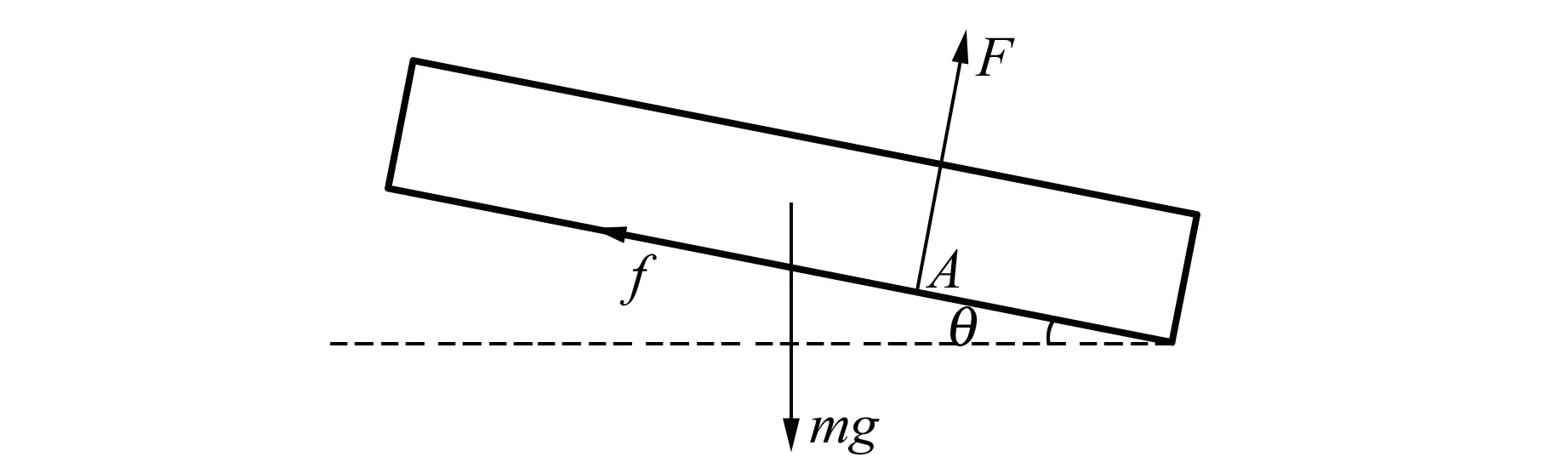
图10 “破碎”现象分析图(最上方圆盘)

由质心运动定理：

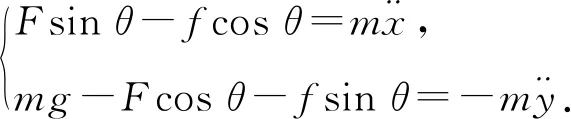
(27)

联立(23)～(27)，得到x，y，θ，F关于t的微分方程组，从而解出F(t)曲线，如图11所示.

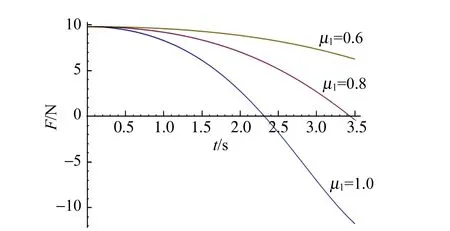
图11 不同μ1下的F(t)解

可以发现，F(t)呈下降趋势，当F下降到0时，即发生“破碎”现象. 当μ1逐渐增大时，可以看到F下降加快，说明圆盘间摩擦越大，越容易发生“破碎”现象. 圆盘在空中分离后便不再有相互作用，因此落地时的速度就是分离时的速度.

2.3 “弹跳”与“夭折”

“弹跳”现象指落地后上方圆盘又弹起的现象，它发生在圆盘的弹性(恢复系数)较大、圆盘厚度较大时. 由于圆盘弹起后不再有摩擦力的作用，因此最终错开的距离主要取决于恢复系数及弹起后各自的水平速度.

“夭折”现象指圆盘塔在最下方圆盘尚未被抽出时即倒塌，它发生在最下方圆盘初速度较小(即突然施加的水平力较小)及圆盘间摩擦较大时. 此情况下塔直接倒塌，不需计算错开距离.

以上2种情况较为简单，本文不做定量研究.

3 实验验证

实验装置如图12所示，其中A为圆盘，B为光电门，C为定滑轮，D为500 g砝码，E为细绳，F为挡光片. 通过从一定高度释放砝码来给予最下方圆盘突然的水平力，通过光电门来测量最下方圆盘的初速度.

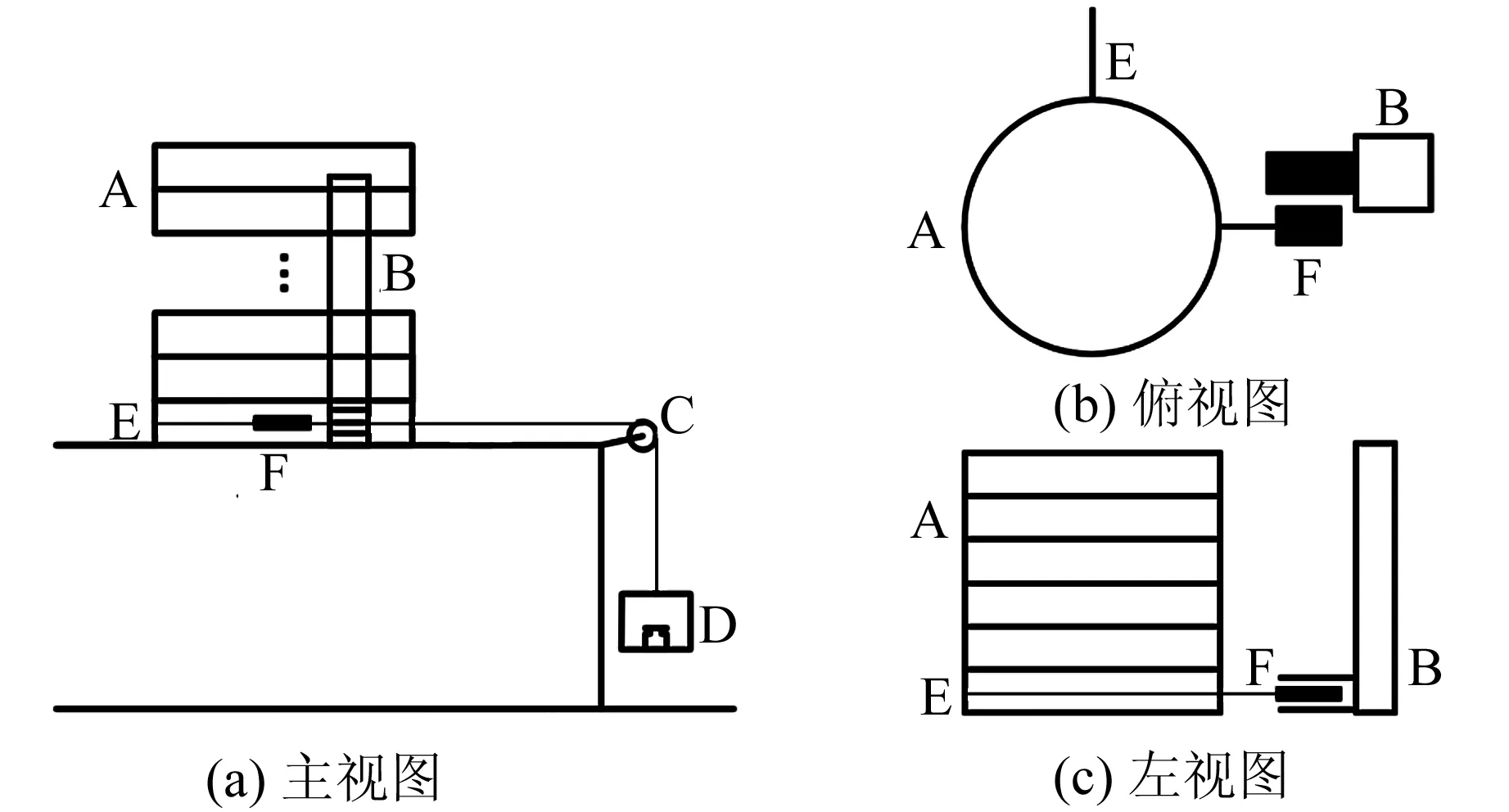
图12 实验装置设计图

为实现题目要求，做了如下规定：

1)绳伸直时砝码要接近地面，保证力的瞬时作用；

2)从一定高度释放砝码，保证足够大的冲量将圆盘抽出；

3)光电门与挡光片的距离等于砝码距离地面的高度，保证光电门所测为最下方圆盘的初速度.

实验装置的优点在于，它能保证相同条件下实验的可重复性：通过在相同高度释放砝码，可以使得最下方圆盘的初速度近似不变.

3.1 圆盘数量的影响

取直径为50 mm、厚度为10 mm、表面磨砂的圆盘为实验对象，保证最下方圆盘初速度v0≈(2.00±0.05) m/s，观察当N=3，4，5，6，7，8时圆盘是否倒塌. 每组实验重复5次，计算圆盘倒塌的概率P.

如图13所示，可以发现，数据呈上升趋势，说明圆盘数量越多，圆盘塔越容易倒塌. 这与理论分析的结果相符合.

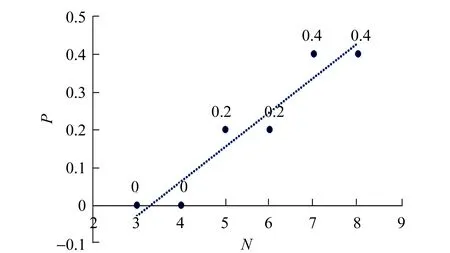
图13 圆盘数量与倒塌概率实验结果

3.2 圆盘直径的影响

取厚度为10 mm直径分别为40，50，60，70，80 mm的圆盘为实验对象，保证最下方圆盘初速度v0≈ (2.00±0.05) m/s，观察当N=6时圆盘是否倒塌. 每组实验重复5次，计算圆盘塔倒塌的概率P.

如图14所示，数据呈下降趋势，说明直径越大，塔越稳定，与理论求得曲面图5中h=0.01 m对应曲线的结论相同.

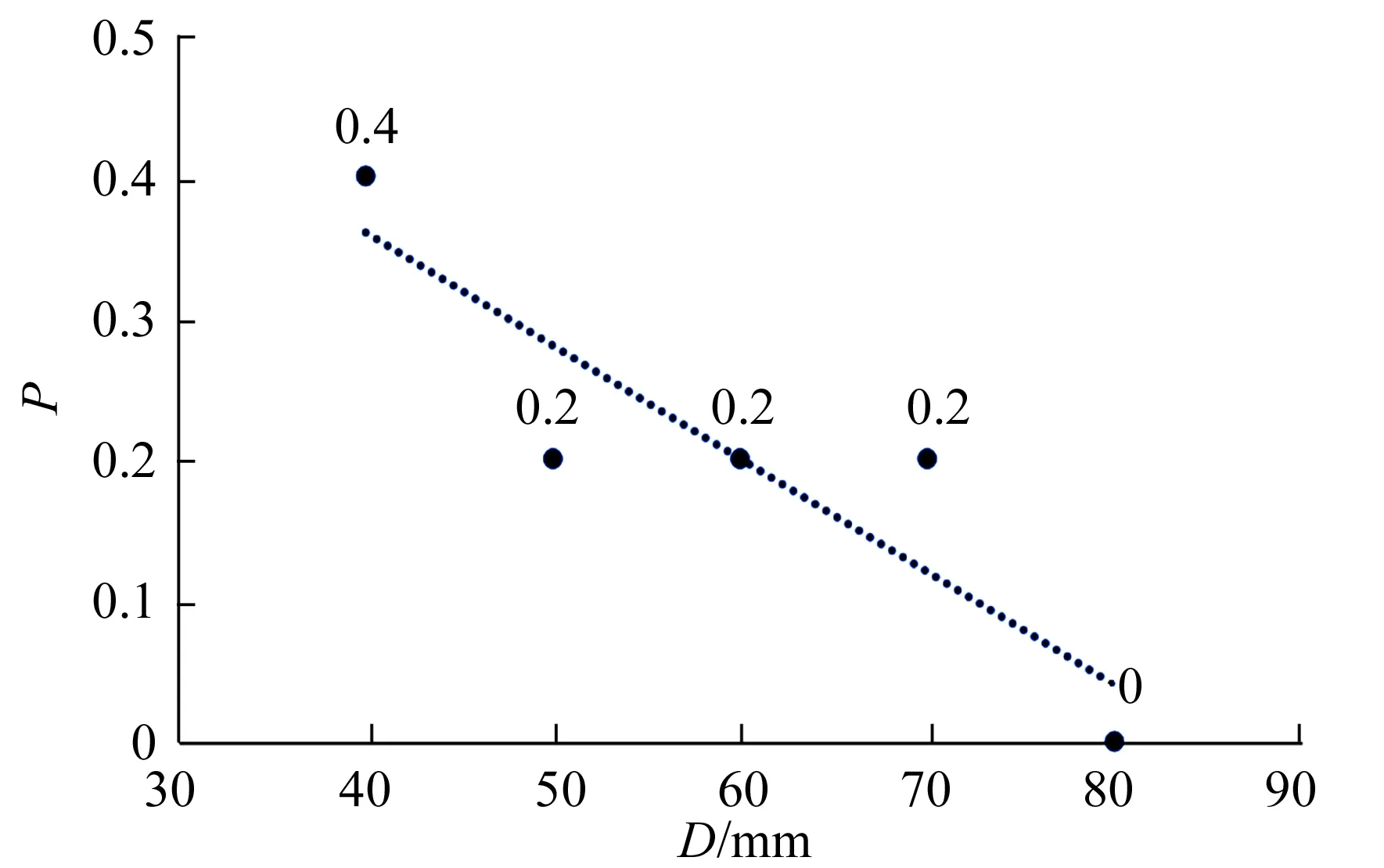
图14 圆盘直径与倒塌概率实验结果

3.3 最下方圆盘初速度的影响

取直径为50 mm，厚度为10 mm，表面磨砂的圆盘为实验对象，堆叠数N=6. 由于实验无法保证每次初速度严格相同，故设置一系列速度区间来探究最下方圆盘初速度的影响趋势. 每个速度区间重复实验5次，计算圆盘塔倒塌的概率P.

速度为1.2～2.8 m/s，区间间隔0.2 m/s，共8个区间，由小到大分别编号为1～8，实验结果如图15所示. 由数据的下降趋势可知，最下方圆盘初速度越大，圆盘塔倒塌概率越低，说明塔越稳定. 这与理论分析结论相符合.

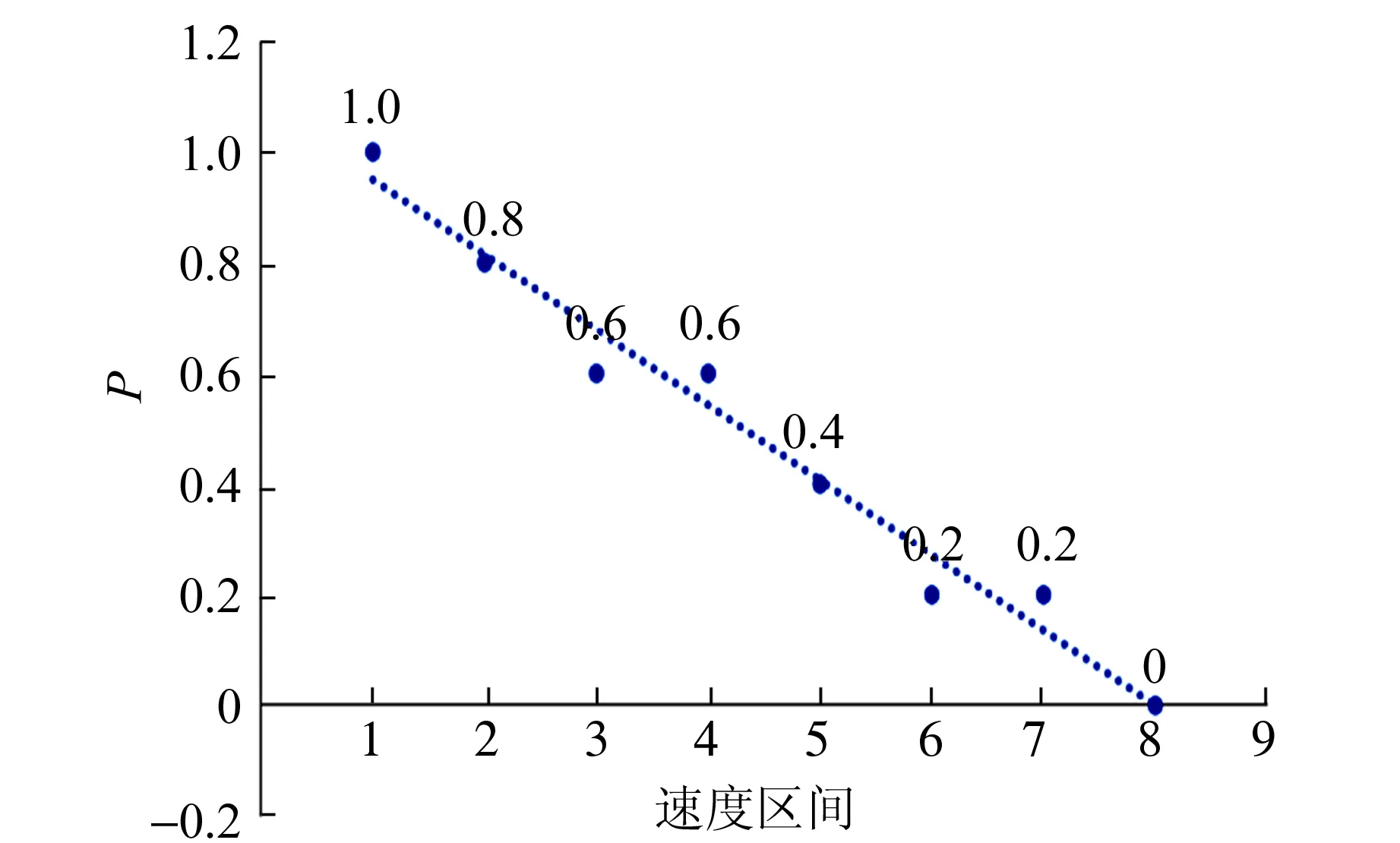
图15 圆盘初速度与倒塌概率实验结果

3.4 圆盘表面摩擦系数的影响

为保证其他条件不变，采取表面处理的方式改变圆盘表面的摩擦系数. 表面处理方式包括：粘贴防滑膜、不处理、轻度打磨、重度打磨. 经测量[4]，4种圆盘的摩擦系数μ1分别为0.66，0.56，0.50，0.42. 多次重复实验，不同摩擦系数圆盘的倒塌概率无法呈现明显的规律. 这可能是由于摩擦系数不同导致的稳定性改变小于随机因素导致的稳定性波动范围，因而其倒塌概率无法产生显著的变化趋势. 实验结果如图16所示.

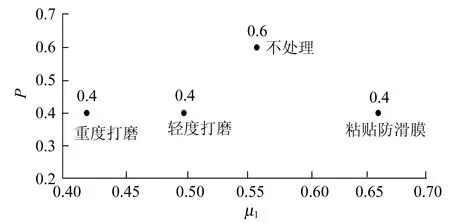
图16 圆盘表面摩擦系数与倒塌概率实验结果

4 结束语

本文对抽出圆盘塔最下方圆盘后，塔是否倒塌的条件做了探究，并对影响塔稳定性的因素进行了分析. 此外，本文对圆盘抽出过程中的4种特殊情况做出了探究. 实际上，圆盘抽出过程还会出现反向错开等情况，此类情况的发生可能有多种原因(如“弹跳”现象或圆盘间摩擦过小)，为避免复杂的分类讨论，本文暂未对这类情况进行深入研究.