基于蛮力搜索的自动分段处理水位流量关系曲线定线的应用

李 劲，李小兰，阚 飞

(1.四川省都江堰东风渠管理处，成都，610081；2.成都赛零信息技术开发有限公司，成都，610000；3.四川省水利科学研究院，成都，610072)

1 前言/背景

水位流量关系曲线是用来描述水文测站所在的基本断面的水位与通过该断面的流量之间关系的曲线。河(渠)道断面流量监测方法多样，水位流量关系曲线法是其中最为常用的、在多数情况下也是较其他方法更为经济的方式。在水文资料整编工作中，水位-流量关系率定是其中重要的一环。

在水文监测站，断面流量随水位的变化而变化，水位随时间的变化过程易于观测且相对准确。故一般不需要连续观测流量过程，而是通过一定次数的实测水位及其实测流量的对应数据资料建立水位与流量的关系曲线，再依据建立的水位流量关系曲线，通过水位插值推算出对应的流量值，把水位变化过程转换为相应的流量变化过程[1]，最后根据转换的流量值计算各业务需要的数据及报表。

东风渠灌区管辖范围内16条干渠主要断面均已建立水情监测设施，依托于灌区信息化建设，当前有131个点位都实现了水位的自动实时监测，绝大多数断面存在单一水位流量关系曲线。灌区每年都按相关测验规范，通过实测断面流量与相应水位，手工绘制拟合水位流量关系曲线。为适应灌区信息化发展，这部分工作需借助计算机来自动完成，传统的计算机定线方法一般都是应用单一的函数来进行，虽然能根据最小二乘法得到最小的残差平方和，但是求得的水位流量关系曲线不能真实体现高水、低水时的数量关系。但将曲线分段后，进行分段拟合，通过蛮力搜索，寻找各点整体最优解，可以在一定程度上解决这个问题。

2 水位流量关系曲线及其拟合方法

2.1 蛮力搜索算法

蛮力搜索算法也称穷举算法，他要求设计者找出所有可能的方法，然后选择其中一种方法，若该方法不行，则试探下一种可能的方法。蛮力法适应能力强，是唯一一种几乎什么问题都能解决的一般性算法。虽然通常情况下蛮力法效率很低，但在数据量有限的条件下，可以作为衡量同类问题更高效算法的准绳。

2.2 最小二乘法原理

最小二乘法是一种在误差估计、不确定度、系统辨识及预测、预报等数据处理诸多学科领域得到广泛应用的数学工具[2]。最小二乘法在19世纪由勒让德发现，他认为，要设法构造出k个方程去求解，关键不在于使每一个方程等号的左右两边都严格相符，这在实际中也是不现实的，而在于要使误差以一种平衡的方式分配到各个方程[3]。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小，形式如下：

目标函数=Σ(观测值-理论值)2

其中：观测值为监测的多组样本，理论值为假设的拟合函数，目标函数即为机器学习中常说的损失函数。最小二乘法的目标是得到使目标函数最小化时的拟合函数的模型。如若有m个只有一个特征的样本：

(xi,yi)(i=1,2,3,…m)

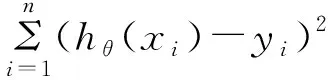
2.3 拟合曲线数学模型

(1)根据曲线的特征，将曲线分为3段，其中，第一段采用幂函数描述两者之间的关系，数学模型为：

Q=a1Ha2

(1)

式(1)中，Q为流量(m3/s)；H为水位(m)；a1、a2为待定的模型参数。

第二、三段采用多项式来描述两者之间的关系，数学模型为：

Q=b0+b1x+b2x2

(2)

式(2)中，Q为流量(m3/s)；H为水位(m)；b0、b1、b2为待定的模型参数。

(2)将水位、流量用最小二乘法分段做一次线性拟合，通过蛮力搜索将给定范围内的误差值最小化，找到全局最小值。

模型目标函数为求理论流量与实际流量的残差平方和最小[4]：

(3)

式(3)中，Qi为第i次实测流量；Q(Hi)为拟合的水位流量关系曲线上查到的第i次实测水位对应的流量。

模型约束条件[5]：

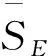
2.4 数据处理流程

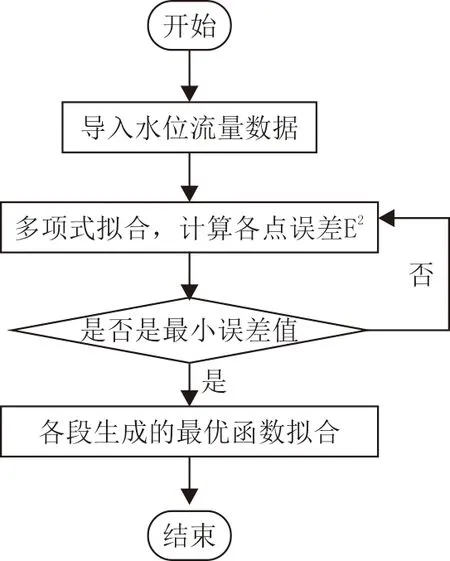
图1 数据拟合、处理流程

步骤一：导入水位流量实测数据；

步骤二：确定分段的数量，通过蛮力搜索，计算在各个实测点的误差；

步骤三：寻找最小的误差值的分段点，生成最优的拟合函数；

步骤四：根据生成的拟合函数，得出水位流量关系曲线。

3 实例分析

3.1 实例1

以徐堰河进口实测水位、流量为例。

表1 徐堰河进口2018年水位流量关系曲线计算成果

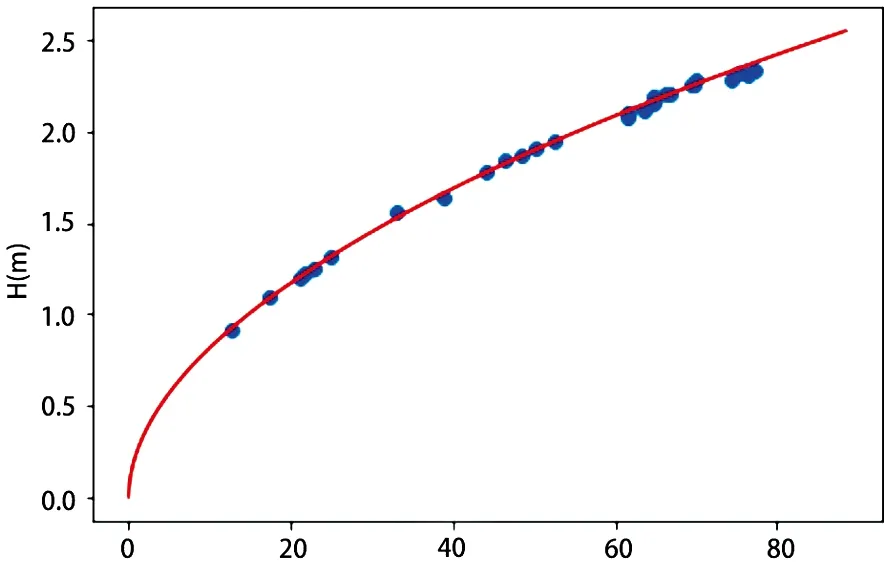
Q(m3/s)

检验结果如下：

符号校验统计量=0.071、适线检验统计量=-0.148、偏离数值检验统计量=0.229、系统误差=0.872%、标准差=1.789%。由此，拟合的曲线光滑顺畅地通过各点群中心，各水位测点均匀分布在曲线两边；拟合成果的精度和各项检验通过定线三检验、满足定线精度要求，通过各项检验。

3.2 实例2

以眉彭干渠进口实测水位、流量为例

表2 眉彭干渠进口2018年水位流量关系曲线计算成果

Q(m3/s)

检验结果如下：

符号校验统计量=0.266、适线检验统计量=-0.1、偏离数值检验统计量=0.005、系统误差=0.423%、标准差=1.164%。由此，拟合的曲线光滑顺畅地通过各点群中心，各水位测点均匀分布在曲线两边；拟合成果的精度和各项检验通过定线三检验、满足定线精度要求，通过各项检验。

4 结论

针对东风渠灌区这种存在大量天然河道的大型灌区，水位流量关系曲线的率定是流量资料整编的一个重要环节，传统的定线方式工作量繁重，还会有不可避免的人为误差。本文采用基于蛮力搜索的最小二乘算法对水位流量关系曲线优化模型进行优化求解，可以使工作人员从繁重的定线工作中解脱，从而提高工作效率。实例表明该算法率定出来的水位流量关系曲线既能很好地满足《水文资料整编规范》(SL 247-2012)关系曲线定线的三性检验(即符号检验、适线检验、偏离数值检验)要求，从而有效地提高水位流量关系曲线的率定效率，很好地满足水文资料整编更高的时效要求。