库岸边坡多级预应力锚杆支护参数优化研究

王小红，汤庆丰

(中国水利水电第十工程局有限公司，四川 都江堰，611830)

1 工程背景

古瓦水电站首部枢纽位于四川省甘孜藏族自治州乡城县境内，是硕曲河干流乡城、得荣段“一库六级”梯级开发方案的“龙头水库”电站，下游为娘拥水电站。工程采用混合式开发，拦河大坝位于擦金许沟口下游约620m处，厂址位于牛棚沟沟口附近硕曲河左岸山体中。枢纽主要建筑物由面板堆石坝、溢洪洞、放空洞、坝后生态机组、引水隧洞及地下厂房系统等组成。硕曲河干流河段坝址控制集水面积3089km2，坝址多年平均流量43.4m3/s，电站引用流量87.8m3/s，水库正常蓄水位3398m，相应库容为2.396亿m3，总库容为2.458亿m3，死水位3320m，调节库容2.228亿m3。

水库库区为典型的河谷地貌，两岸的山势陡峭，地质条件十分复杂。特别是库区左岸距离坝址200m至400m的区域存在较多的断层、层内和层间错动带、原生和构造裂隙等不良地质构造，在蓄水过程中会产生比较复杂的应力变形，一旦发生失稳破坏，必将对工程的安全运行造成极大威胁[1]，因此需要采取必要的加固措施。该边坡为长100m、宽6m的三级均质边坡，拟采用预应力锚杆对其进行分级支护。其中各级边坡的高度比较接近，均为10m，自下而上各级边坡的坡脚依次为70°、60°和50°，边坡的土体为均质黏土，其厚度大于20m。前期调查中采用对数螺旋滑裂面法对其进行分析，结果显示其最小安全稳定系数为1.03，存在一定的危险性，需要进行分级加固处理。

2 FLAC 3D计算模型

2.1 FLAC 3D及其基本原理

FLAC 3D是美国Itasca咨询公司开发的一款基于拉格朗日有限差分计算程序的三维数值模拟软件，在岩土工程、结构工程、温度以及流体等诸多领域具有广泛的应用[2]。在实际应用过程中，软件得到不断发展和完善，不仅功能日渐健全，计算速度也不断加快，对节省使用者的时间和精力起到了十分重要的作用。另一方面，该软件也具有比较简单的操作界面，可以为使用者带来比较直观的分析，成为岩体工程领域的一款主流分析软件[3]。

在边坡支护领域问题的求解过程中，涉及力学平衡方程、几何方程以及模型本构方程等[4]。在利用FLAC 3D软件进行数值计算过程中，首先利用网格剖分功能将几何模型划分为有限个四面体结构单元，并将模型的整体应力-应变计算过程中分解、转化到各个计算单元和节点上，然后在各个节点上利用有限差分进行近似求解，最终完成模拟计算[5]。

2.2 计算模型的构建

本次研究的对象属于多级预应力锚杆支护边坡的模拟[6]，为了方便计算模型的构建以及尽量减少各种因素对计算结果的负面影响，研究中结合边坡的实际情况，做出如下假设：一是假设库岸边坡为均质黏土体边坡，因此按照平面应变问题进行支护结构的分析；二是鉴于边坡所处部位的地下水埋藏深度较大，在模拟计算过程中不考虑地下水和孔隙水对计算结果的影响；三是假设所使用的预应力锚杆为理想的弹性材料，并且可以和周围的注浆体和土体完全粘结，也就是完全满足变形相容条件。

根据工程的原始设计，以井字形布置边坡的各级锚杆，每级边坡竖直布置4排锚杆，编号分别为1-4、5-8和9-12。锚杆的竖向间距设置为2.50m。锚杆钢筋选用的是HRB335级，锚具的型号为JLM-32，对每排锚杆施加的预应力为120kN。对模型的底面施加固定位移约束，左右两个边界施加法向位移约束，坡面以及坡顶为自由面[7]。根据相关设计，模型的锚杆计算参数如表1所示。

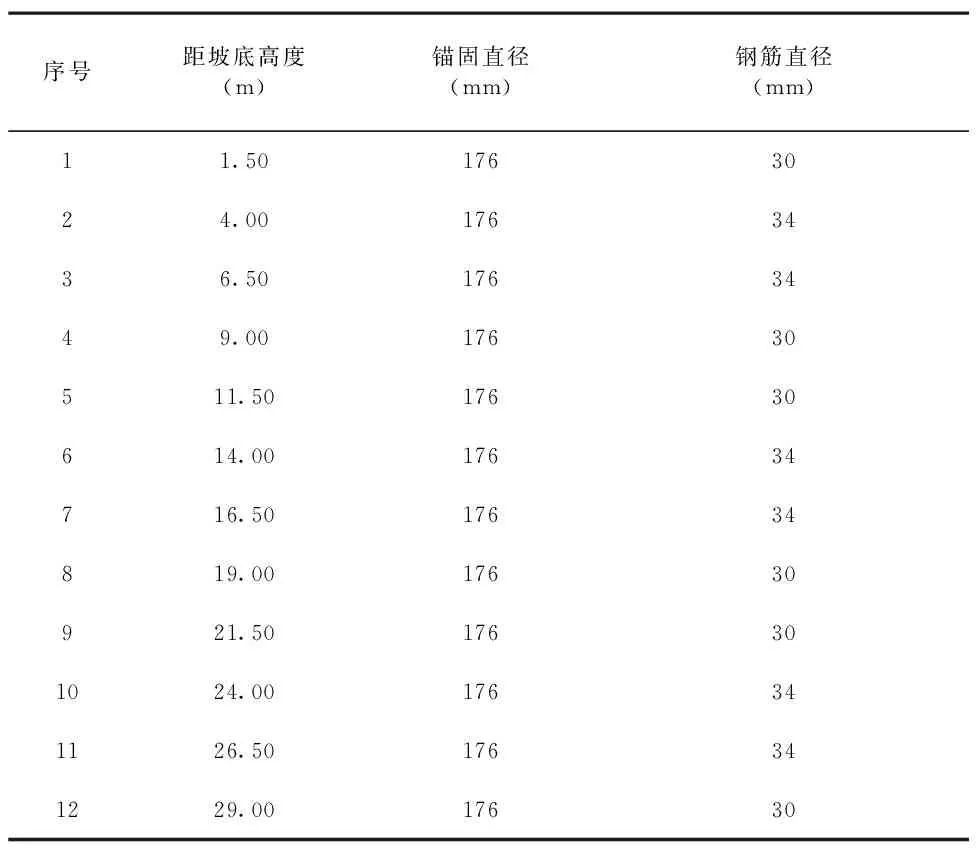
表1 锚杆计算参数

为了减小边界效应对模拟结果的影响，同时照顾模型计算的简洁性，参考相关研究经验，模拟研究过程中将坡体向下延伸25m，坡脚向前延伸32.2m，构建起三维有限元模型[8]。对模型采用非结构化网格划分，利用Cable锚杆结构单元进行计算模型的构建，模型划分为10217个网格单元和13247个计算节点，结果如图1所示。

图1 三维有限元模型示意

3 计算结果与分析

3.1 锚杆长度优化结果

根据工程实际和相关研究成果，设计6.0m、7.0m、8.0m和9.0m四种不同长度的锚杆，利用上节构建的数值计算模型，对不同锚杆长度条件下的最大轴力和水平位移进行计算，结果如表2所示。由表中的计算结果可知，锚杆的最大轴力随着锚杆长度的增加而增加，锚杆长度由6.0m增加到8.0m时，最大轴力的增长幅度较大，但是进一步增加到9.0m时，最大轴力的增加幅度较为有限。由此可见，锚杆的长度并不是越长越好，一味增加锚杆的长度并不是科学的方法，并会显著增加施工成本。从边坡的水平位移计算结果来看也是如此，边坡的水平位移量会随着锚杆长度的增加而减小，锚杆长度由6.0m增加到8.0m时，边坡水平位移的减小幅度较大，再进一步增加锚杆长度时，边坡位移量减小幅度较为有限。综合上述计算结果，锚杆的最佳长度应该为8.0m。

表2 不同锚杆长度的最大轴力和水平位移

3.2 锚杆间距的优化结果

根据工程实际和相关研究成果，设计2.5m、3.0m、3.5m和4.0m四种不同的锚杆水平间距，利用上节构建的数值计算模型，对不同锚杆水平间距条件下的最大轴力和水平位移进行计算，结果如表3所示。由表中的计算结果可知，锚杆轴力随着锚杆水平间距的增大而呈现出先增大后减小的趋势，当锚杆的间距为3.5m时，锚杆轴力达到最大，为76.48kN。由此可见，锚杆间距过大或者过小，均不利于锚杆作用力的有效发挥，当锚杆间距为3.5m的情况下，可以发挥最大的加固作用。从边坡的水平位移来看，其随着锚杆间距的增加呈现出先减小后增大的趋势，当锚杆间距为3.5m情况下，边坡的水平位移量最小，为31.5mm。由此可见，锚杆间距过大或者过小，均不利于边坡水平位移的有效控制，当锚杆间距为3.5m的情况下，可以实现最好的水平位移控制作用。综上所述，从最大轴力和边坡的水平位移来看，锚杆的水平位移最佳值为3.5m。

表3 不同锚杆水平间距的最大轴力和水平位移

3.3 锚杆角度优化结果

根据工程实际和相关研究成果，设计10°、15°、20°和25°四种不同的锚杆角度，利用上节构建的数值计算模型，对不同锚杆角度条件下的最大轴力和水平位移进行计算，结果如表4所示。由表中的计算结果可知，锚杆轴力随着锚杆角度的增大而增大，原因是锚杆支护角度增大的情况下，其发挥的作用会不断减小，进而导致边坡产生较大的变形，使边坡作用在锚杆上的荷载明显增加，其面临的轴向拉伸变形也会加大，最终导致锚杆最大轴力的增加。从边坡的水平位移来看，会随着锚杆支护倾角的增大而增大。由此可见，从控制边坡位移的角度来看，应该尽量选择小角度的锚杆安装方式。但是，相对于10°的锚杆支护角度而言，15°的锚杆支护角度的边坡水平位移和最大轴力变化不大，但是施工更方便，因此推荐15°的锚杆支护角度。

表4 不同锚杆角度的最大轴力和水平位移

3.4 最优方案与验证

综合上述分析，最优方案应该是锚杆长度8.0m、锚杆间距3.5m、锚固角为15°。为了验证该方案的合理性，利用构建的模型对其进行数值模拟，其结果如图2所示。由模拟结果可知，在该方案条件下，边坡的安全系数为1.316，锚杆受到的最大轴力为71.23kN。显然，该方案可以兼顾边坡的安全性和经济性，实现了参数优化研究的最终目标。

图2 最优方案数值模拟结果

4 结论

本次研究以古瓦水电站上游库岸均质边坡为例，利用数值模拟研究的方法对锚杆加固参数进行优化研究，并获得如下主要结论：

(1)锚杆的最大轴力随着锚杆长度的增加而增加，边坡的水平位移量会随着锚杆长度的增加而减小，但是锚杆长度超过8.0m时变化幅度较为有限，因此锚杆的最佳长度应该为8.0m。

(2)随着锚杆水平间距的增大锚杆轴力呈现出先增大后减小的趋势，边坡的水平位移则呈现出先减小后增大的趋势，因此，锚杆间距以3.5m为宜。

(3)从控制边坡位移的角度来看，应该尽量选择小角度的锚杆安装方式。但是15°的锚杆支护角度的边坡水平位移和最大轴力变化不大，但是施工更方便，因此推荐15°的锚杆支护角度。

综合上述分析，最优方案应该是锚杆长度8.0m、锚杆间距3.5m、锚固角为15°。由模拟结果可知，在该方案下，边坡的安全系数为1.316，可以兼顾边坡的安全性和经济性。