基于订单体积指数和需求相关性的多巷道货位分配优化

何立华， 任海朝

（中国石油大学（华东）经济管理学院，山东青岛 266580）

仓储作为物流活动中的一个重要环节，在制造业、物流业中起着承上启下的作用. 据统计［1］，拣选作业时间占整个仓储作业时间的30%～40%，拣选成本占仓库运营成本的65%以上. 不同的货位分配会对仓库的拣选效率产生不同影响［2］.

货位分配问题是经典的仓储管理问题［3］. Wang等［4］最早提出了基于物料的订单体积指数（cube-per-order index），即COI原则，一种物料的COI值等于一段时间内它的总存储空间与该段时间内的周转率之比. 其值越小越要将该物料存储在靠近仓库出入口的货位上，该指标同时考虑了物料所需的总存储空间和周转率，大大提高了物料的存储效率. 后来Heskett［5-6］又将COI原则进一步应用到仓库布局中. Yang和Nguyen［7］基于COI原则，利用主成分分析对物料进行分类分级，并根据COI系数进行存储位置分配. 王洋和谢勇［8］提出了基于COI的改进分类存储策略，对货物先按COI值分类，再按照定位存储进行货位分配. 李明琨和张杨平［9］将COI储位分配方法与巷道作业平衡改进策略相结合，提出绝对分巷道存储模型和相对平均与最大值控制模型两种储位分配改进方法.

上述货位分配主要考虑物料的单一属性，如订单体积指数，没有从物料的多个属性进行综合考虑. 仅依靠COI 原则进行货位分配，会出现需求相关性大的物料被分配到的货位相距较远的情况，从而增加拣选距离. 所以部分文献以物料之间的需求相关性为指标进行优化研究. 肖建和郑力［10］扩展了仅考虑两个物料成对需求的情况，构建相关数学模型，通过遗传算法进行求解. Jane和Laih［11］根据物料的需求相关性对其分类，并采用随机存储策略分配货位. 李建斌等［12］建立基于产品出库频次和相关性的优化指标，构建整数线性规划模型，运用模拟退火算法求解. 邓爱民等［13］基于时间，以货物出入库效率高、相似货物摆放在一起和货物移动距离最短三个指标构建模型，并用遗传算法求解. 周亚云等［14］综合考虑了物料的需求关联和周转率，基于货位指派规则建模并用谱聚类算法求解.

为提高拣选效率，一些学者抛弃传统仓储布局，转为研究拣选效率更高的非传统仓储布局，并进行货位分配优化. Gue和Meller［15］提出了Flying-V和Fishbone非传统布局方式. 刘建胜等［16］在Flying-V布局基础上，考虑货物出入库效率最高和货物存放重心最低，建立多目标优化模型，并将遗传算法和粒子群算法结合进行求解. 虽然以上两种仓储布局相较于传统布局降低了仓库拣选总距离，但也降低了仓库的空间利用率［17］.

传统仓储布局和非传统仓储布局大都是窄巷道式，这以最低的成本提高了空间利用率，但可能会使得被高频拣货的巷道产生拥堵［18］. 另外，仓库同时进行的多张订单拣选任务也可能会导致距离出入口较近的巷道发生作业拥堵. 同时，单纯依靠COI原则，由于体积差异，可能导致某些需求相关性大的物料，体积小的被分配到距离出入口较近的货位，体积大的被分配到距离出入口较远的货位，不利于同时拣货，影响拣货效率. 本文采用多巷道存储策略解决COI原则导致的靠近出入口的巷道拥堵问题，同时考虑需求相关性，解决COI原则导致的相关性大的物料因体积差异被分配到的货位相距较远的问题.

本文以仓库中的物料和货位为研究对象，以物料的订单体积指数和需求相关性为优化指标，采用多巷道存储策略，以订单体积指数加权的最小距离和需求相关物料所处货位之间的最小距离之和为目标，建立数学模型，并通过改进的遗传算法进行求解.

1 货位分配模型构建

对仓库布局做如下假设：

每条巷道左右两侧各有一排货架，货架为背靠背式；允许一货多位；货位至出入口的距离计算采用城市距离，且规定同一巷道同一列的货位到出入口的距离相同，即不考虑层数对货位到出入口距离的影响.

模型参数设定如下：

根据COI原则和需求相关性，采用多巷道存储策略，构建如下目标函数.

1）最小化COI加权下物料所处货位到仓库出入口的距离：

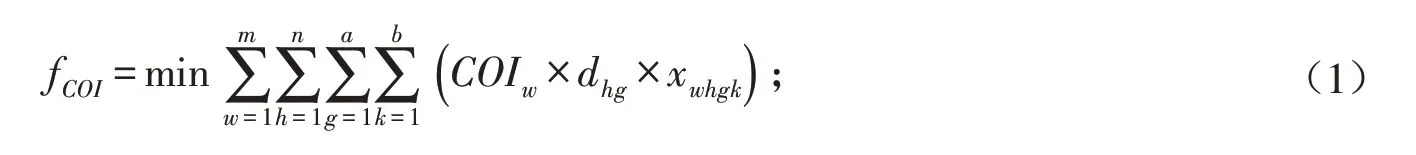
2）最小化具有需求相关性的物料所处货位之间的距离：

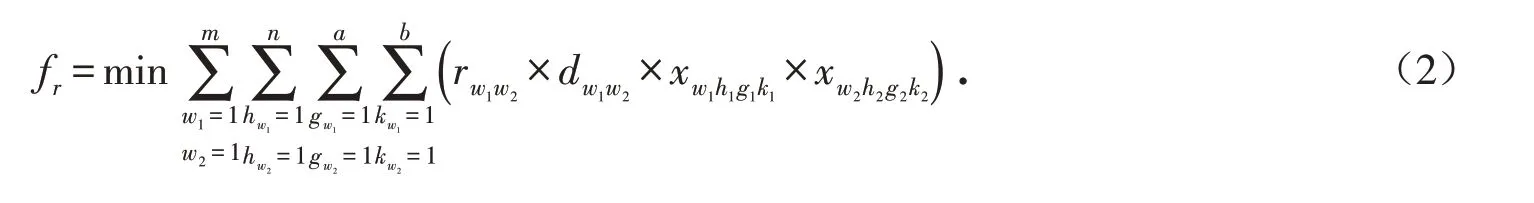
将目标函数（1）和（2）加权转化成单目标函数：

约束条件：

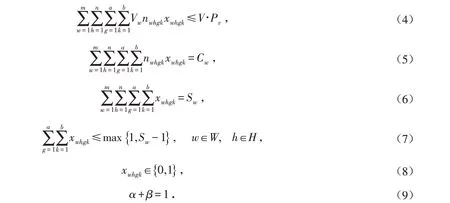
式（4）表示分配到该货位的所有物料的总体积不大于该货位的可利用空间；式（5）表示存储在各个货位上的物料数量之和与该物料总量相等；式（6）表示允许同一种物料被存储在不同的货位上；式（7）表示将需要超过一个货位的物料进行多巷道存储；式（8）为0～1变量，xwhgk=1 表示物料w存储在第h巷道第g列第k层的货位上，否则xwhgk=0；式（9）为目标权重.

其中，相关参数计算如下：

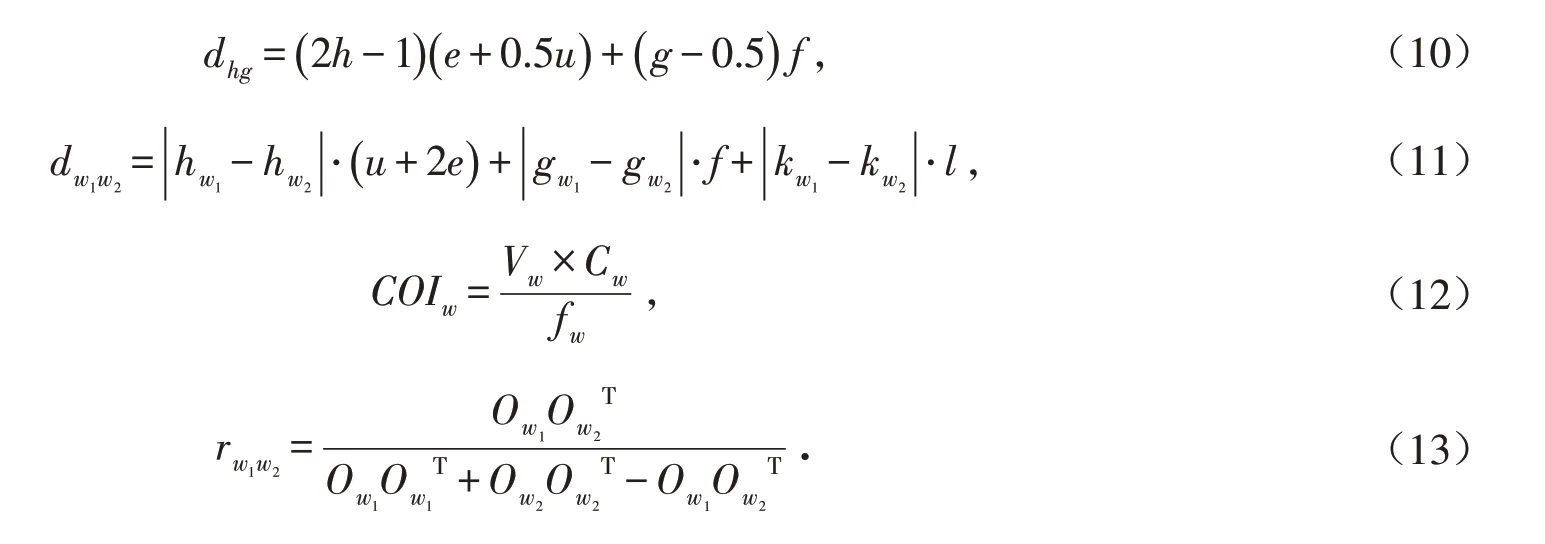
式（10）表示第h巷道第g列货位距离出入口最近的城市距离；式（11）表示两种物料所处的货位之间的距离；式（12）表示物料w的订单体积指数；式（13）表示物料之间的需求相关度［18］.

2 货位分配模型求解

本文考虑的两种距离因素下的货位分配优化问题，本质是旅行商问题的延伸，是NP难问题，相较于经典的旅行商问题，本文所研究的优化问题具有以下复杂性：

1）参数众多. 需要将众多物料及仓库参数经过计算转化成距离.

2）目标特殊. 具有两个关于距离的优化指标.

货位优化问题是一个NP难问题，所以只能使用启发式算法进行求解［19］. 因为该问题涉及参数众多、目标特殊以及该模型会产生非常多的可行解，同时也会产生很多局部最优解，寻找这些可行解并从中寻求最优解的工作量较大，要求求解算法具有良好的局部搜索能力和全局搜索能力，采用改进的遗传算法就能很好地解决这一问题.

2.1 编码

根据货位分配的目标函数及物料和货位编号的特点，采用整数编码的方式. 每条染色体由货位所处的巷道数、列数及层数组成. 一条染色体表示一种货位分配的可行解，即一种可行的货位分配方案. 仓库布局平面图如图1所示，假设有9条巷道，每条巷道两侧共20列货架，每列货架有3层. 基因编码示意图如图2所示.

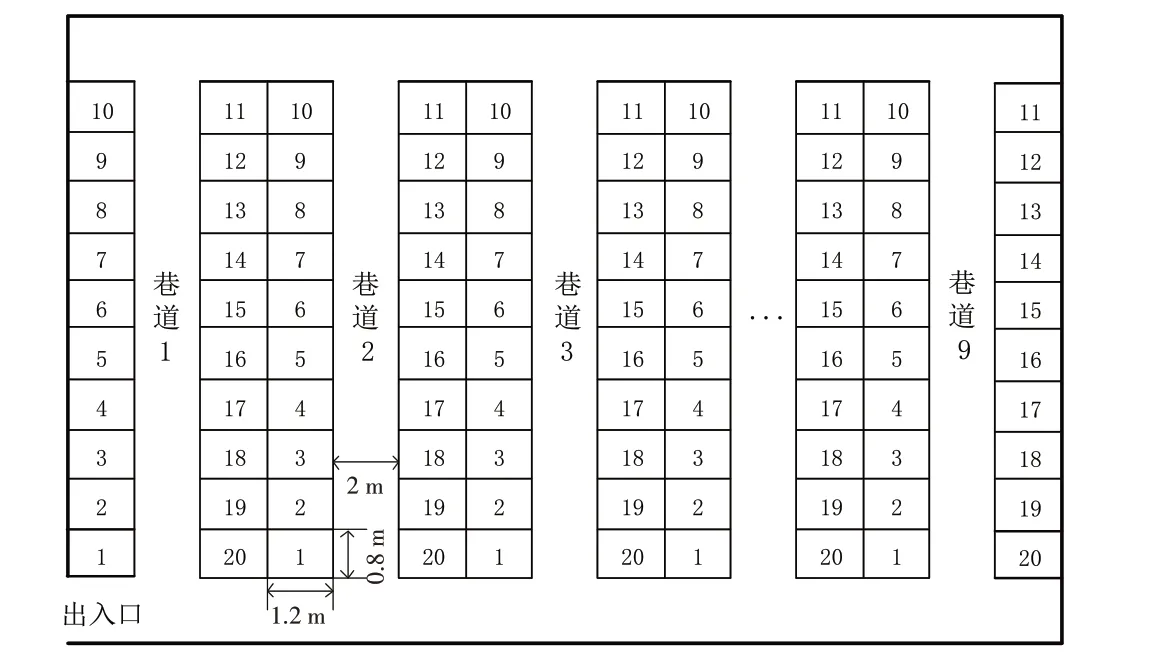
图1 仓库布局平面图Fig.1 Schematic diagram of warehouse layout

图2 基因编码示意图Fig.2 Schematic diagram of gene coding

在上述示意图中，如（1，1，1）表示位于第一巷道第一列第一层的货位. 根据物料数量所需的∑Sw个货位，将物料放于前∑Sw个货位，即可获得其中一种货位分配方案. 将货位顺序随机打乱，即可获得其他货位分配方案.

2.2 初始化种群

由于本文涉及的货物种类和货位数量较多，问题的可行解也会非常多，为了保证遗传算法的全局搜索能力，保证其具有遍历整个解空间的能力，采用随机产生的初始种群，在初始种群的基础上进行后续遗传操作. 本文选取种群规模大小为200.

2.3 适应度评价

适应度函数在进化过程中起到优胜劣汰的作用. 适应度函数的选取直接影响到遗传算法的收敛速度以及能否找到最优解. 遗传算法中的适应度值要求越大越好，其值越大越利于被选中. 本文目标函数为最小化，所以采用目标函数的倒数作为适应度函数. 适应度函数如下：

2.4 遗传操作

遗传算法（Genetic Algorithm，GA）是一种模拟生物进化的随机搜索算法，采用选择、交叉和变异的操作来进行种群的进化［20］.

选择操作，轮盘赌和锦标赛选择是常用的选择算子，但若仅采用轮盘赌选择，有时会出现即使适应度值较大的个体也不被选中的情况，而仅采用锦标赛选择，不论是二元锦标赛还是四元锦标赛，每次选择出的个体数量又有限. 为了保证算法的全局搜索能力且尽可能快的使算法收敛，对选择操作进行改进，提出轮盘赌选择和锦标赛选择相结合的选择算子，即同时采用轮盘赌和锦标赛选择，对分别通过两种算子选择出的最优个体进行比较，然后再次选择出二者中适应度值较大的个体，进而提高算法的全局搜索能力并加快算法的收敛. 图3为改进的选择算子示意图.

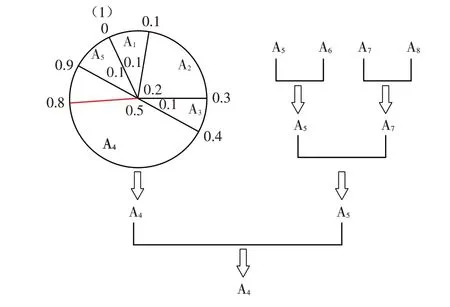
图3 轮盘赌+锦标赛选择算子示意图Fig.3 Schematic diagram of roulette+tournament selection operator

交叉操作，传统的两点交叉已不再适用于本文研究问题，若直接简单交换两个父代中交叉点之间的基因片段，则会在同一个父代中出现基因重复的情况，进而导致子代出现不可行解，因此本文提出改进型两点交叉，交叉操作示意图如图4所示. 父代1和父代2为两个可行解，随机生成两个交叉点，两个父代交换两个交叉点之间的基因片段，如果交换的基因片段中带有和原来父代个体上相同的基因片段，则将原有父代基因中重复的基因用交换前的基因进行替换.

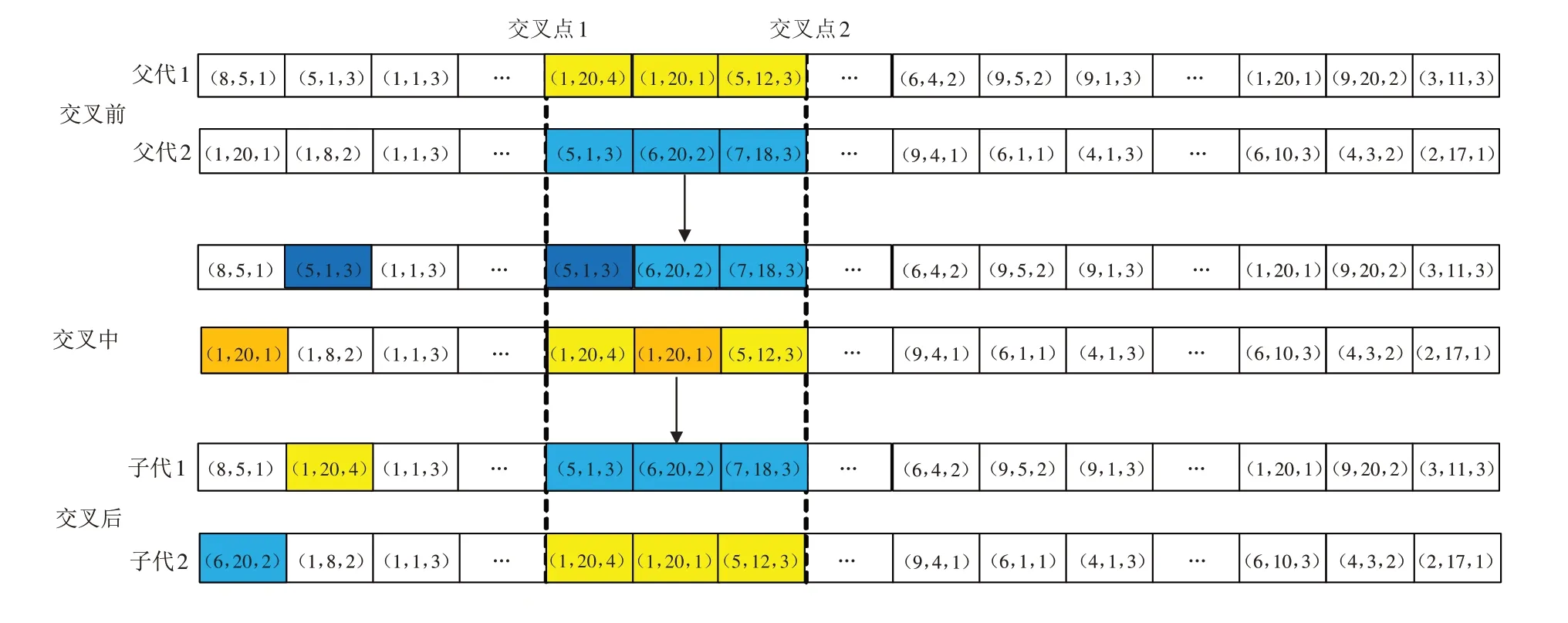
图4 交叉操作示意图Fig.4 Schematic diagram of cross operation

变异操作是实现种群多样性的重要手段，是跳出局部最优进行全局寻优的重要保证. 在染色体中随机生成一个变异起始点和一个变异终止点，将两点之间的基因片段进行完全倒置. 变异操作示意图如图5.

图5 变异操作示意图Fig.5 Schematic diagram of mutation operation

2.5 终止操作

进化终止条件为达到固定的进化代数，当迭代次数达到规定次数之后，停止迭代并输出最优解. 本文选取MAXGEN=250.

3 算例分析

本节选取一家汽车电子产品制造企业的仓库进行算例分析.

3.1 仓库布局及物料信息

该制造企业仓库共有9条巷道，巷道宽2 m，每条巷道两侧共有20列货架，每列货架高3层，仓库布局平面图如图1所示，货位长1.2 m，宽0.8 m，高0.5 m，空间利用率为90%. 选取某段时间内该仓库中需要进行货位分配的10种物料进行货位分配.

为了探究本文构建模型及设计算法的有效性，特针对以下两种情况进行求解：

1）不同仓库规模对货位分配结果的影响，即改变仓库的巷道数，选取小、中、大三种仓库规模，相应地，n=2、n=4 和n=9 .

2）不同权重取值对最终货位分配结果的影响，即α从0每隔0.1取值到1，相应地，β从1每隔0.1取值到0.本文运用MATLAB2018对模型进行仿真.

3.2 结果分析

本文针对小、中、大三种仓库规模的不同权重取值（其中β=1-α）进行比较分析，结果如表1～3所示.

表1 小规模算例的求解结果（n=2）Tab.1 The solution result of a small scale calculation example

表2 中规模算例的求解结果（n=4）Tab.2 The solution result of a medium scale calculation example

表3 大规模算例的求解结果（n=9）Tab.3 The solution result of a large scale calculation example

优化前采用随机存储的分配方式，优化过程采用本文提出的考虑订单体积指数和需求相关性，同时采用多巷道存储策略进行货位分配，由小、中、大三种规模的30个算例优化前后结果及改进百分比可知，运用本文提出的分配策略及改进后的遗传算法对货位分配进行优化求解，针对小、中、大三种仓库规模的算例，改进效果均较为明显.

下面给出了一个中规模算例的具体数据及结果. 物料信息如表4所示，物料在该段时间内的100个历史订单中被订购情况如表5所示，表6为物料之间的需求相关系数.

表4 物料信息Tab.4 Material information

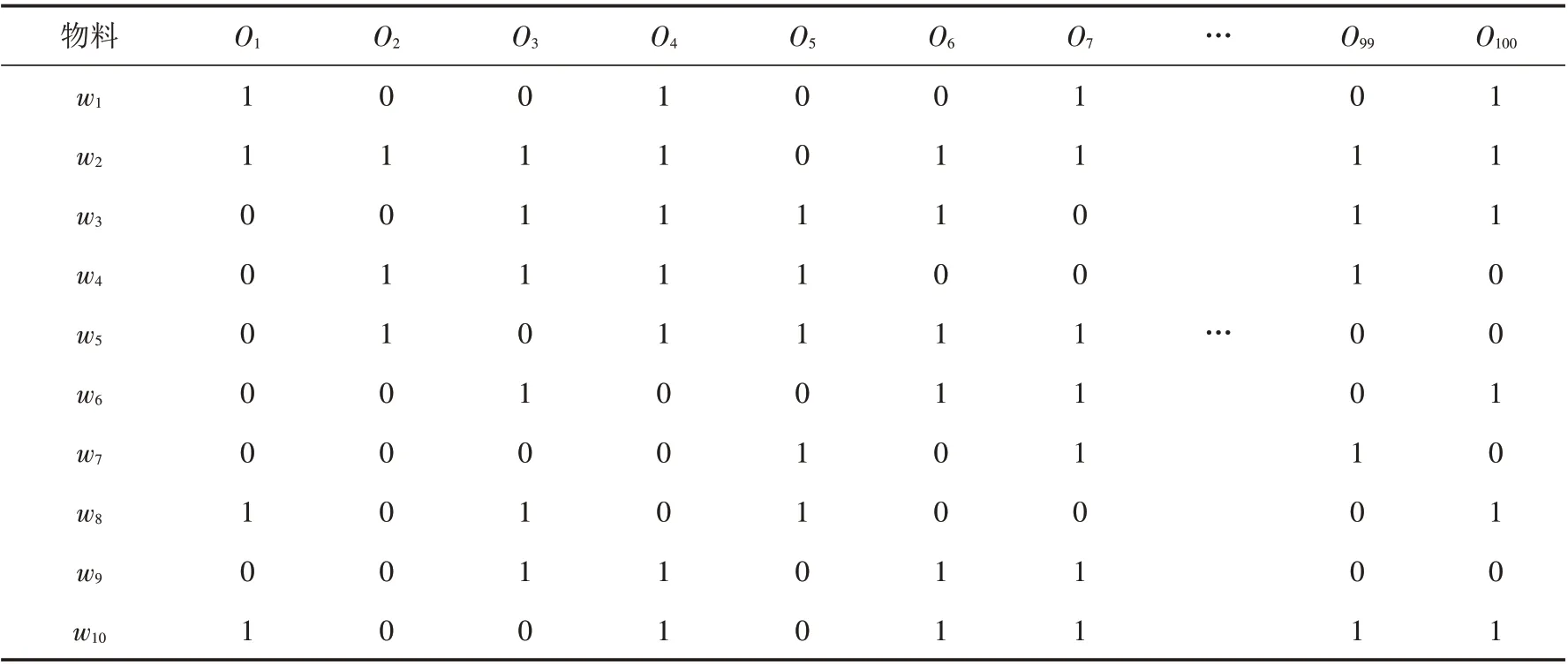
表5 物料在某段时间内100个订单（O1～O100）中被订购情况Tab.5 Material being ordered in 100 orders within a certain period of time

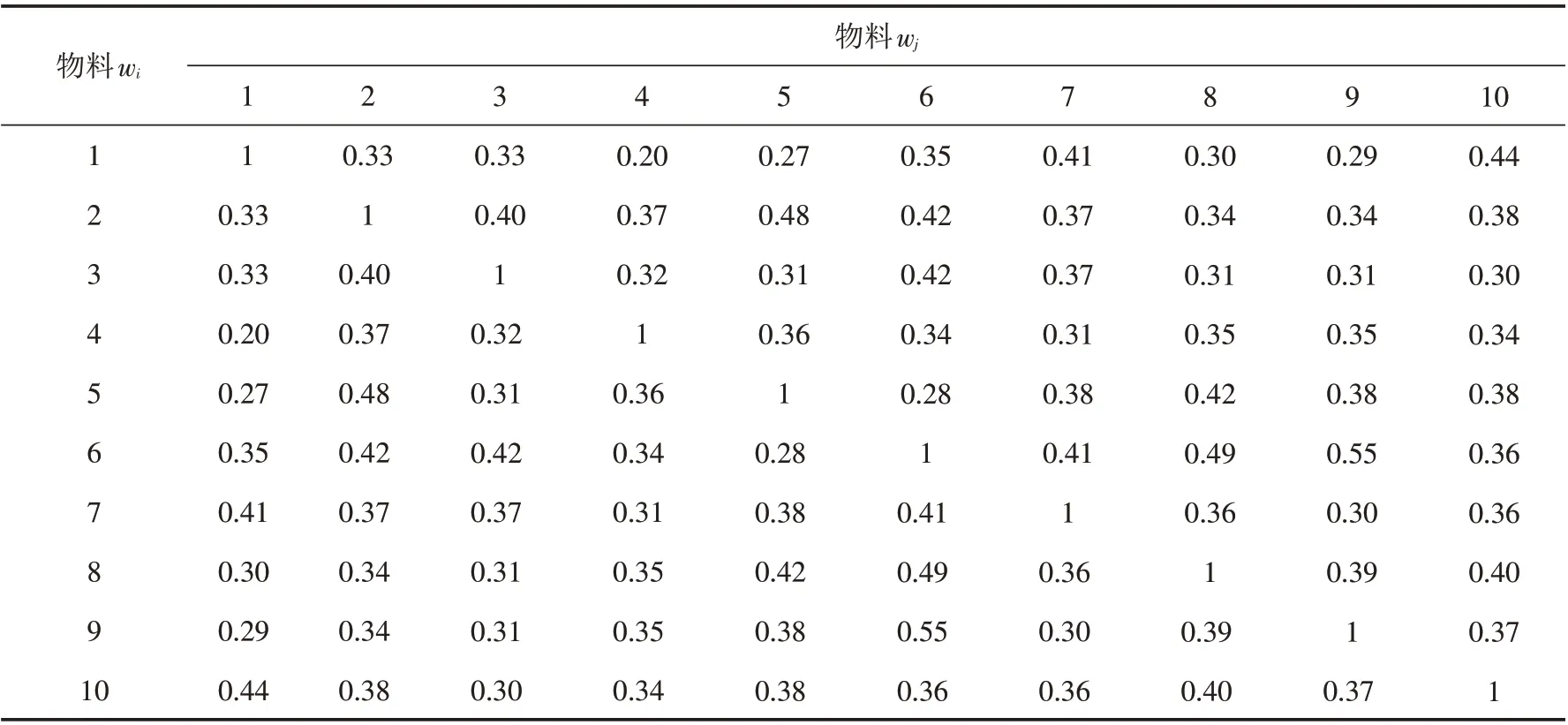
表6 物料需求相关系数(rwiwj)Tab.6 Correlation coefficient of material demand

根据图6中两个单目标及总目标函数的进化趋势可以看出，进化前30代目标值处于下降趋势且进化速度较快，而120代后目标值趋于稳定数值，说明了改进的算法具有良好的局部和全局搜索能力. 图6 a、b、c变化趋势说明，随着进化代数的增加，相关货物正在聚集存储，且整体向靠近仓库出入口的方向存储. 根据表2及图6 d可知，当α=0 时，表示只考虑需求相关性指标；当α=1时，表示只考虑订单体积指数指标；当α的取值在0～1之间时，表示同时考虑需求相关性和订单体积指数. 由目标权重的变化可知，其取值不同，对总目标函数影响较大，即对拣选总距离影响较大，但不同权重取值对改进百分比影响不大. 表7为优化前后的货位分布情况.

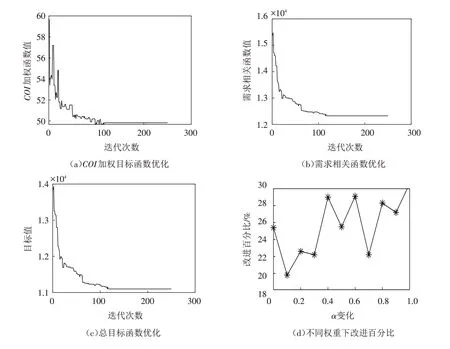
图6 迭代图Fig.6 Iterative figure

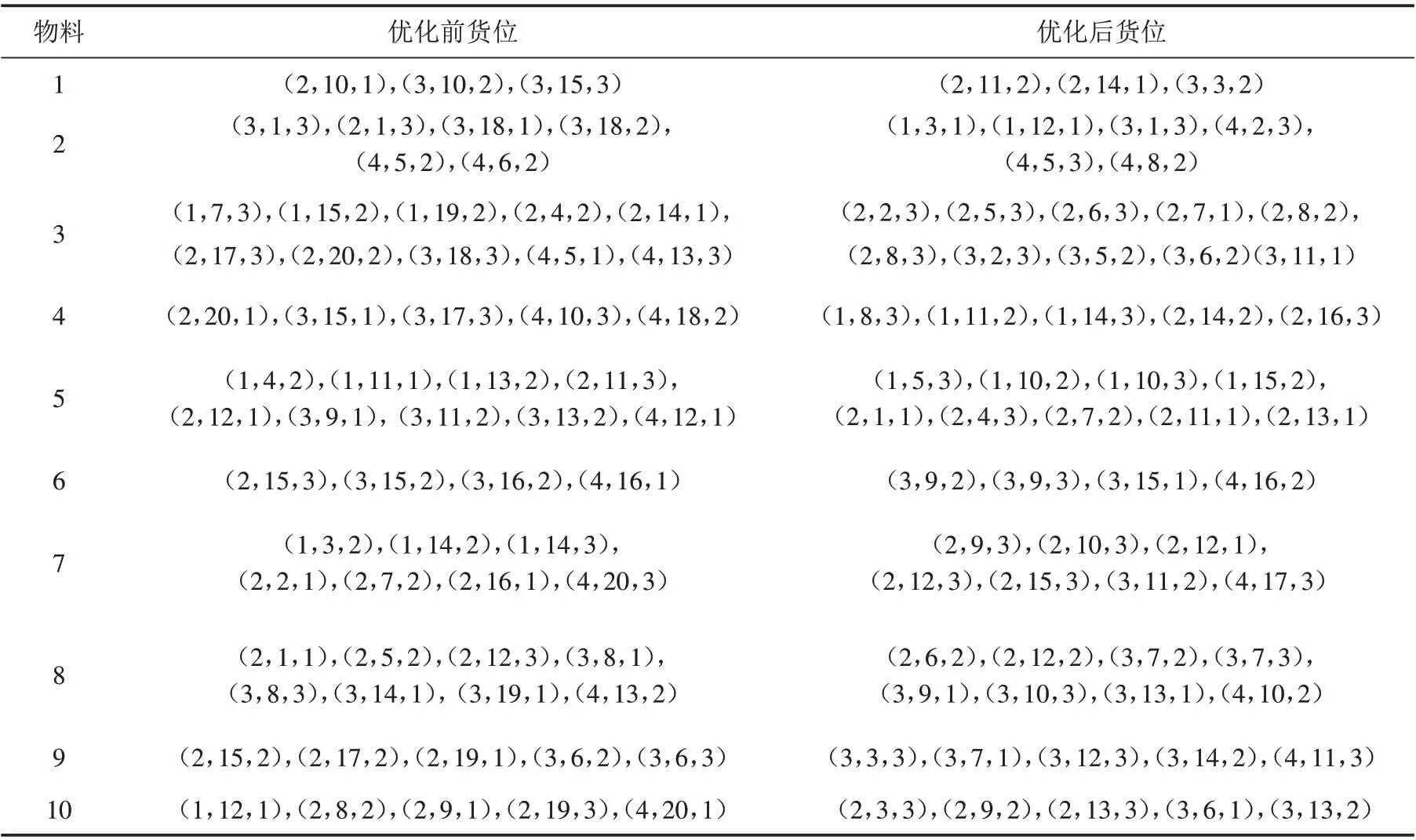
表7 优化前后的货位分布情况Tab.7 Goods location distribution before and after optimization

4 结论

本文对现有货位分配策略进行优化改进，同时考虑COI原则和需求相关性原则，并采用多巷道存储策略进行货位分配. 本文构建模型及改进算法主要贡献包括：①解决了仅考虑COI原则产生的具有需求相关性的物料被存储在相距较远的货位和靠近仓库出入口的巷道拥堵问题；②验证了构建模型及改进的求解算法对小、中、大三种规模算例的适用性和可行性；③分析了不同权重取值对最终拣选总距离的影响，为决策者根据实际情况进行权重选择提供了依据.

由于优化目标仅是从提高拣选效率角度出发，所以构建的优化模型仅仅是有关距离的函数，未考虑货位分配过程中的其他影响因素，如时间、成本等，未来的研究可以从多个维度综合考虑来提升仓库拣选效率.