基于威布尔分布数字特征的电机滚动轴承早期故障诊断

姜海燕

（湖南铁道职业技术学院轨道交通电务技术学院，湖南株洲 412001）

机械设备运转所产生的振动信号中包含了丰富的设备状态信息，统计资料表明，旋转机械的故障中大约有60%～70%由振动引起［1］. 滚动轴承振动信号中包含了大量相关的故障信息，但是这些故障信息与振动信号之间没有直接的对应关系，因此怎样将反应轴承运行状态的敏感信息从轴承振动信号中提取出来变得至关重要. 状态识别能否成功，在很大程度上取决于反映状态的特征量的选择. 目前常见的振动信号的时域、频域和时频域统计指标，常被选作轴承状态监测和故障诊断中的特征量，这些特征量在实际应用中都各有局限性［2-3］. 因此，如何发现、构造和挖掘新的对状态变化更加敏感、更有普适性的潜在特征，是滚动轴承乃至机械设备监测诊断领域一直致力于解决的工程实际问题.

在旋转机械中最常见的一个部件是电机滚动轴承，对于滚动轴承而言，由于长期重复工作，且具有一定的载荷力和工作表面的接触力，因此极易引起疲劳故障，如：磨损、裂纹、压痕、点蚀、老化，这些缺陷经过一定时间的积累和扩展会导致轴承失效. 在可靠性分析研究中，研究人员往往用威布尔分布函数来描绘这种由疲劳故障引起的轴承失效. 威布尔分布是瑞典人威布尔在1939年提出的一种描述材料疲劳强度的分布模型，因其模型参数可以较好地反映随机载荷下机械产品及其零部件的疲劳寿命和疲劳强度，故在可靠性研究中得以广泛应用［4-8］. 随着科技的发展和不断的研究，近几年来，有不少文献中提到利用威布尔分布函数监控在线状态数据，从而对设备进行故障诊断和预测等研究［9-16］，并在精确度较高的发动机和飞行器等机械结构故障预测中也被应用［17-19］，但将威布尔分布的数字特征作为特征量来表征运行结构的特征并不多见.

本文提出一种基于威布尔分布数字特征的电机滚动轴承早期故障诊断方法，首先采集故障轴承的振动信号对采集后的振动信号进行降噪等处理，接着建立相关的统计分布模型，验证模型的有效性，选择最佳的威布尔分布模型，然后对选择的模型求取其形态参数和尺度参数，并估计出其特征量均值、方差、二阶原点矩、三阶中心矩、中位数和偏度，最后利用SVM模式识别器对特征量进行模式识别和故障分类. 实验结果证明了本文所提方法的有效性.

1 基于威布尔分布数字特征的轴承特征信息提取

1.1 威布尔分布的数字特征

1939年由瑞典人威布尔提出了一种描述材料疲劳强度的分布模型，即威布尔分布模型. 威布尔分布模型的尺度参数和形态参数能较好地反映随机载荷下机械产品及其零部件的疲劳寿命和疲劳强度，因此在可靠性研究中得以广泛应用［2-7］.

经退化和处理之后，常用的两参数威布尔分布概率密度函数（Probability Density Function，PDF）和累积密度函数（Cumulative Density Function，CDF）分别为［2-7］：

式中：其形态参数β＞0；尺度参数η＞0. 威布尔分布函数在可靠性分析领域中应用时，主要是通过分析和记录产品的故障、拆修等事件数据来估计产品的物理特性，其中x表示为产品的失效时间或寿命. 而在特征提取和故障诊断技术应用领域中，通常是对机械设备的运行状态进行实时数据监控，然后对采集到的实时数据进行分析，提取其表征机械设备运行的状态信息，因此在信号处理和故障诊断领域x也可以为采集到的原始振动信号. 对原始振动信号建立威布尔分布模型，其模型的相关数字特征如下.

威布尔分布模型的均值

其中：Γ 为伽马（gamma）函数.

威布尔分布模型的方差

威布尔分布模型的二阶原点矩

威布尔分布模型的三阶中心矩

威布尔分布模型的中位数

威布尔分布模型的偏度

1.2 滚动轴承特征信息提取

通过大量文献检索表明，当滚动轴承发生故障时，会影响其接触面积以及与接触面积的受力情况，因此从在线采集的振动信号中会观察到振动信号已经发出了明显的变化. 而振动信号的异常变化，会使振动信号的相关特性发生变化，如：信号时域特征的幅值、平均值等参数和频域特征量频率方差、根方频率等参数都会发生相对应的变化. 为了更好地识别和诊断滚动轴承故障发生在何种部位以及故障的类型，提高滚动轴承故障诊断的识别率，可以通过分析某些特征量的变化信息来实现滚动轴承的故障诊断. 而威布尔分布模型作为统计分布模型中的一种典型和常用的分布模型，在其他可靠性分析和机械设备数据监控和故障预测中也被广泛应用. 为此，本文提出了一种基于威布尔分布数字特征的电机滚动轴承早期故障诊断方法.其方法的具体实施步骤如下.

1）试验样本的获取

通过加速度传感器采集滚动轴承运行时的原始振动信号，振动信号的采样数据集为Xsj（j=1，2，…，N），采样点数为N.

由（1）或（2）式可知，样本数据必须满足x≥0，为此，对原始采样信号做如下预处理：

式中：δ为一经验值，一般取δ≤0.1×min(|Xsj|).

本文中的一个样本是以1024个采样点组成的，则采样数据集Xsj中包含的样本个数为M=N/1024，由于威布尔分布函数的局限性，将采样数据集经（9）式预处理之后得到的数据集为Xj，将预处理的数据集Xj顺序构成试验样本集Xm（m=1，2，…，M），其中某一个样本的数据序列为xmi（m=1，2，…，M），i为采集的数据点（i=1，2，…，n；n=1024）.

2）模型的验证

为了验证滚动轴承振动信号符合威布尔分布模型的变化规律，随机抽取试验样本集Xm中的任意一个样本xmi，m∈｛1，2，…，M｝，将样本中的数据严格重新排列，按照数据幅值增大的顺序排列，得到一组新的序列为（i=1，2，…，n；n=1024），用期望秩估计的累积密度函数（CDF）值：

绘制对应的威布尔分布概率纸图，如果试验数据沿一条直线均匀分布，则符合威布尔分布函数模型，为了进一步验证试验函数符合威布尔分布函数模型，可以对模型进行拟合优度检验.

拟合优度检验的重要数量指标为判定系数（Coefficient of Determination），判定系数用R2表示，其表达式如下：

判定系数的取值范围为0 ≤R2≤1，R2越大说明实际数据样本越接近于我们所选择的模型，即与选择的模型拟合程度越高.

3）分布参数的特性分析与特征提取

在设备失效的研究中，威布尔函数中的分布变量x表示为产品的失效时间或寿命，那么形态参数和尺度参数分别表征产品的不同失效类型和特征寿命. 在本文中，主要分析形态参数、尺度参数以及威布尔分布函数的数字特征是否具有有效反映轴承运行状态变化的特性. 如果某参数能反映出轴承运行状况，甚至对不同类型的故障轴承具有较好的模式可分性，则其可用于滚动轴承故障信息的特征提取.

4）SVM模式识别

将提取出的滚动轴承特征信息作为SVM分类器的输入信号，对滚动轴承故障信息进行识别. 由于SVM分类器主要是进行两两分类，而本实验中的滚动轴承的故障类型有四类，则需要构建两个训练支持向量机，最后利用训练好的SVM多分类器对滚动轴承的测试样本进行故障模式识别. 通过模式识别的正确率来验证特征提取方法的有效性，并总结威布尔分布参数和数字特征对表征滚动轴承故障信息的敏感性.

2 实验仿真

2.1 轴承数据描述

将基于威布尔数字特征的故障特征提取方法应用于滚动轴承故障诊断试验. 试验采用美国Case Western Reserve University轴承实验中心的试验装置（如图1所示）和数据，测试轴承型号为6205-2RS JEM SKF.

图1 轴承试验装置Fig.1 Bearing tester

由固定在感应电机输出轴机壳上的加速度传感器进行数据采集，采样频率为48 kHz. 本文中使用的数据是在不同转速（1797、1772、1750、1730 r/min）与不同负载（0、1、2、3 HP）工况条件下，对正常状态、内环故障、滚动体故障、外环故障四种不同故障类型和故障点直径为0.177 8 mm 的情况下，记录加速度传感器的测量输出，共获得对应16种运行状态原始振动信号的16个采样数据集，包括正常轴承信号、内环故障信号、滚动体故障信号和外环故障信号各4个. 设第k种运行状态采样数据集的采样点数为Nk（k=1，2，…，16），以1024 个采样点为一个样本，则第k种运行状态采样数据集中包含的样本个数为Mk=Nk/1024，对16 个采样数据集分别按（9）式进行预处理后（取δ=0.01），构成16 个试验样本集（m=1，2，…，Mk；k=1，2，…，16）. 从每个试验样本集中随机抽取20个样本作为训练样本，余下样本用于测试样本.

2.2 模型的选择与检验试验

按第1节步骤（2），试选威布尔分布模型.=ln为横坐标、y(=ln(-ln(1-F() ))为纵坐标，分别绘制16种不同运行状态下滚动轴承信号的威布尔分布概率纸图，这里仅给出如图2 a、b、c、d所示正常状态、内环故障、滚动体故障和外环故障的威布尔分布概率纸图. 可见，轴承振动信号的数据分布在威布尔概率纸上近似成一条直线，据此可初步判断样本数据服从威布尔分布.

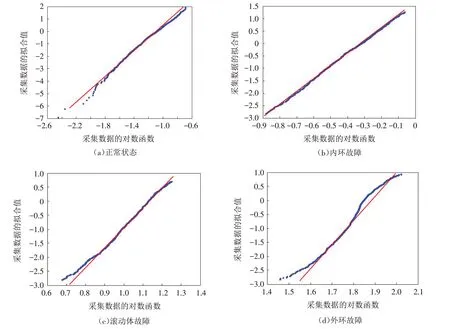
图2 部分状态的威布尔分布概率纸图Fig.2 Weibull distributions of partial states

为了进一步验证模型的有效性，分别对正常运行状态、内环故障状态、外环故障状态和滚动体故障状态的预处理的振动信号通过式（11）计算其四种运行状态下的威布尔分布模型的断定系数，、、和分别表示正常状态、内环故障、外环故障和滚动体故障的判定系数. 其判定系数如表1所示，结果表明所选模型的合理性.

表1 威布尔分布在部分运行状态时的判定系数Tab.1 Determination coefficients of Weibull distributions in partial operational states 单位：/%

2.3 威布尔分布数字特征的特性分析试验

为分析威布尔分布模型的尺度参数和形态参数以及数字特征对轴承振动信号中信息变化的敏感性，针对前述16 种运行状态进行了相同负载、相同故障程度、不同故障类型（共4 个试验）试验，并对试验中形态参数、尺度参数和数字特征的估计值特性进行了分析. 限于篇幅，仅给出①负载为1 HP、故障点直径为0.007 mm、故障类型不同时的形态参数和尺度参数的估计值特性曲线，如图3所示；②负载为0 HP、故障点直径为0.007 mm，故障类型不同时的威布尔分布数字特征值的均值和方差、三阶中心距和二阶原点矩的估计值特性曲线分别如图4、5所示.

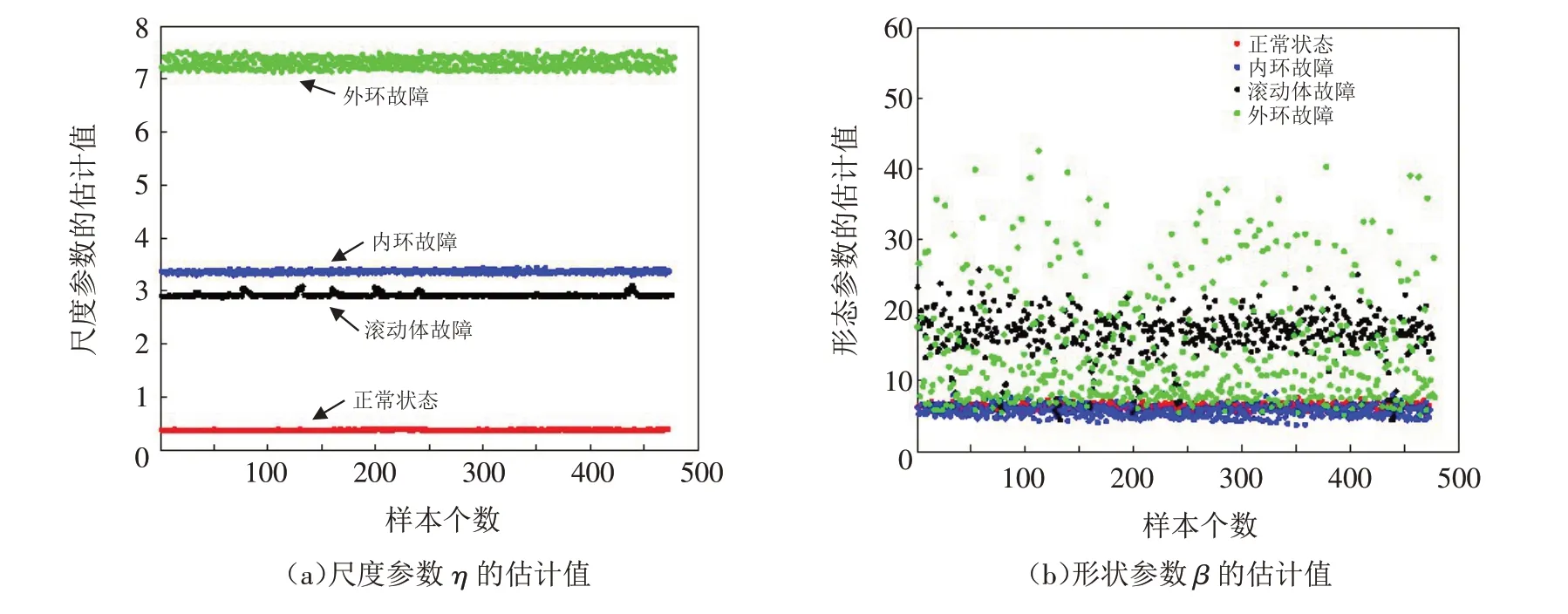
图3 负载为1 HP、故障点直径为0.007 mm、不同故障类型时的参数估计值Fig.3 The parameter estimation values for different fault types with the load of 1 HP and the fault point diameter of 0.007 mm

图4 负载为0 HP、故障点直径为0.007 mm、不同故障类型时的均值和方差估计值Fig.4 The mean and variance estimation values for different fault types with the load of 0 HP and the fault point diameter of 0.007 mm

可见，尺度参数、均值和二阶原点矩等威布尔的数字特征不仅可以很好地区分轴承运行状况的正常与否，而且可以有规律地、敏感地捕捉不同工况下不同类型轴承故障的变化，而形态参数和方差等数字特征在模式空间不具有良好的聚类性和可分性. 可以认为，尺度参数、均值和二阶原点矩等威布尔的数字特征非常适合用作轴承运行状态监测和故障诊断的特征量.

图5 负载为0 HP、故障点直径为0.007 mm、不同故障类型时的二阶原点矩和三阶中心矩估计值Fig.5 The second-order origin moment and third-order central moment estimation values for different fault types with the load of 0 HP and the fault point diameter of 0.007 mm

2.4 SVM的识别结果

针对前述16 种运行状态进行了相同负载、相同故障程度、不同故障类型（共4 组试验16 种状态）试验.为了对比其他参数的不可分性，分别将尺度参数、均值、二阶原点矩、中位数、偏度、形态参数、方差、三阶中心矩作为特征量输入支持向量机分类器进行故障识别，识别结果分别标记为A、B、C、D、E、F、G、H，其SVM的识别结果如表2所示.

从表2的识别结果可知，威布尔分布的尺度参数、威布尔分布的数字特征均值、二阶原点矩、中位数和偏度都能很好地表征滚动轴承的特征信息，对早前故障的轴承识别正确率达到100%；而其形态参数、方差和三阶中心矩则对滚动轴承的特征信息具有不可分性.

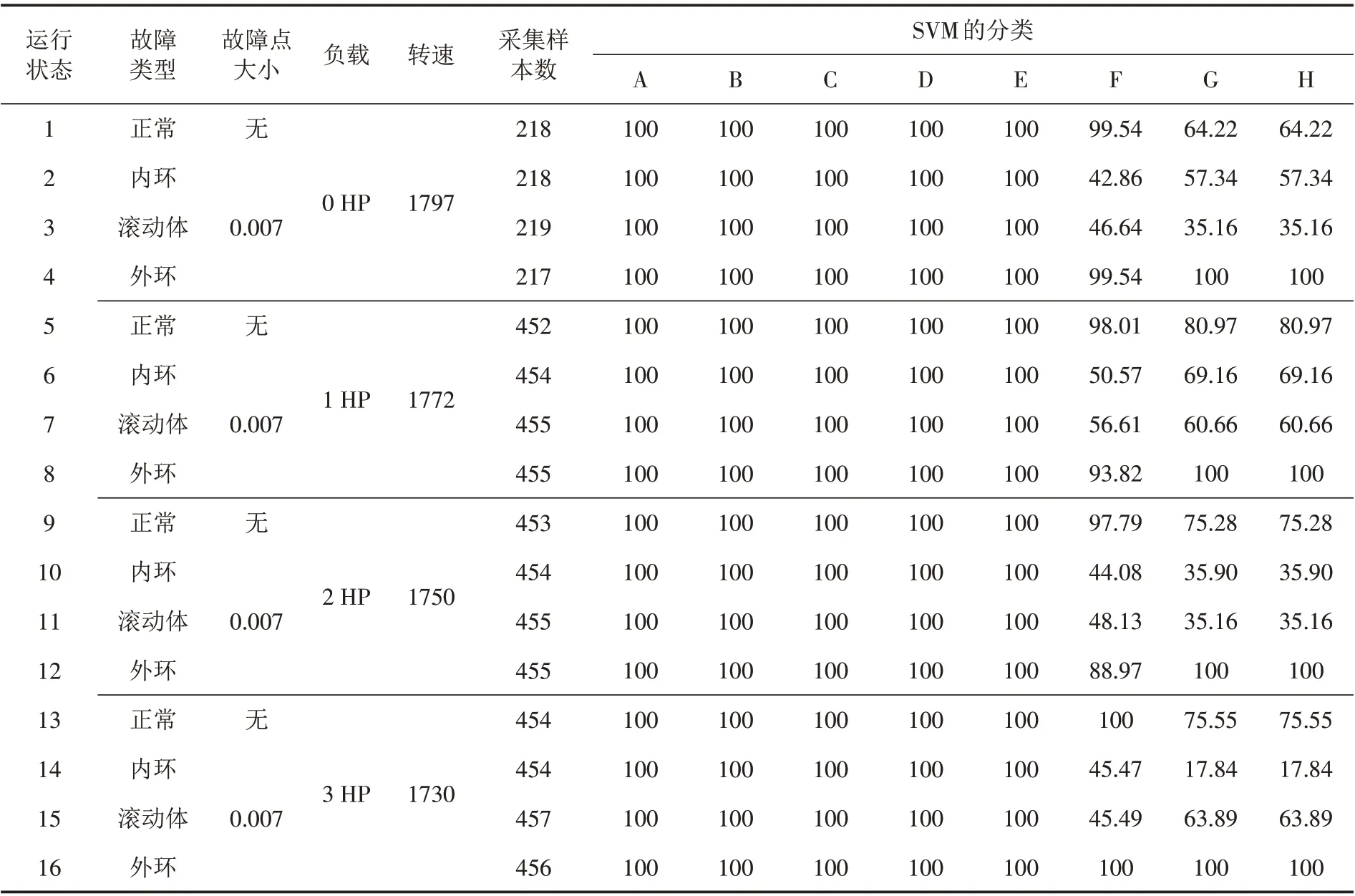
表2 相同负载、相同故障程度、不同故障类型的SVM识别结果Tab.2 SVM identification results for different fault types with the same load and the same fault degree

3 结论

本文提出了一种采用轴承振动信号的威布尔分布模型的尺度参数和数字特征中的均值、二阶原点矩、中位数和偏度作为表征轴承运行状态的特征量，并通过试验分析证明了上述特征量能有效地用于滚动轴承状态监测与早前故障诊断. 本文的研究结论可进一步推广，将威布尔分布参数和数字特征应用于监测机械设备的运行状态与故障诊断，因此具有一定的理论价值和广泛的应用前景.