基于连续小波变换的蒺藜植被覆盖度预测

刘昕,杨光*,林群,张龙英,陈昊宇,王宁,刘峰,刘晨

(1.内蒙古农业大学沙漠治理学院，呼和浩特 010018；2.山西大学计算机与信息技术学院，太原 030006)

遥感技术的发展为植被覆盖度提取提供了极大便利，可以快速、准确地获取某一区域的植被覆盖度，已被广泛应用于生态学。目前，国内外学者在监测植被各项指标等方面做了较多研究。就植被覆盖度而言，有学者提出了一种新的估算方法，利用红边斜率反演植被覆盖度代替传统的归一化植被指数(normalized difference vegetation index，NDVI)反演植被覆盖度模型[2]；以红边参数、蓝边参数以及吸收特征参数为输入量来估算植被覆盖度达到了良好的效果[3]；高永平等[4]采用无人机获取可见光影像，用差异植被指数、归一化绿化差异指数、归一化绿蓝差异指数等建立植被覆盖度回归模型，结果表明，利用无人机获取数据提取出指数所建立的模型精度更高、更准确；上述研究都利用光谱特征参数作为自变量来反演植被覆盖度的精度。近年来，由于小波变换具有多尺度、可以由粗到细逐步观察信号的变化、丰富的小波基函数等优点[5]，在血压、心电图、气象学、通用信号处理、语言识别、计算机图形学等多领域都得到了广泛应用。目前，小波变换大多数用于预测土壤有机质、植物叶绿素、植物冠层含量等方面，但未对植被覆盖度进行深入研究。

本文以固沙植被蒺藜(TribulusterrestrisL.)为研究对象，探讨了研究植被覆盖度与两波段原始光谱植被指数之间的关系，采用连续小波变换(continuous wavelet transform，CWT)对植被原始光谱反射率进行不同尺度的分解，分析各尺度小波系数与植被覆盖度之间的相关性，找出每个尺度所对应的最优波段，以植被指数与最优小波系数为自变量，利用偏最小二乘法(partial least square，PLSR)、支持向量机(support vector machine，SVM)两种算法建立植被覆盖度的估算模型，对比分析选出最优模型，旨在为植被监测提供地面的理论支持。

1 材料与方法

1.1 植被选取

试验区位于内蒙古呼和浩特市托克托县(北纬40°5′—40°35′，东经111°2′—111°32′，图1)。试验于2019年7—8月进行，选取蒺藜为研究对象，土壤为沙壤土。将GIS影像与地形地貌、土壤质地和植被状况相结合，进行实地调查并选择植被类型(固沙)与土壤相适宜的试验地，选取具有代表性的20个点作为地物光谱测试点，共测量70组植被光谱数据。

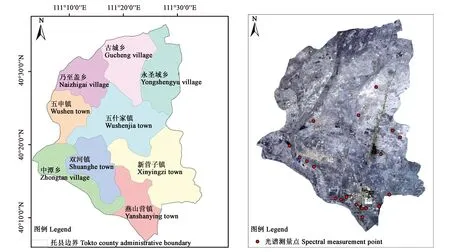
图1 研究区地理位置图及采样点分布Fig.1 Geographical position map of study area and location of sampling points

1.2 光谱数据采集与处理

采用SVC HR-1024便携式地物光谱仪(美国Spectra Vista公司)测定，光谱有效范围为350～2 500 nm，波段个数为1 024，最小积分时间1 ms，信号采集方式为蓝牙传输[6]。选择晴朗无云或少云无风天气在10:00—14:00进行采集，传感器探头距离蒺藜冠层的高度为30～60 cm，每个光谱数据的测定时间设置成5 s，每一组植物测定10条光谱曲线，取其平均值作为该样点的光谱反射率值。

利用光谱仪自带软件SVC HR-1024 剔除光谱曲线变异较大的数据，进行融合。由于在测量时波段之间存在相应的能量差异和光谱仪器自身因素等影响，导致光谱曲线会产生一些噪声，采用DB5与Savitzky-Golay方法进行去燥与平滑，并将光谱数据重采样至10 nm。

1.3 植被覆盖度测算

利用图像提取植被覆盖度，每测一组光谱，需在相同位置与高度进行垂直拍照，测量中使用的数码相机型号为Canon EOS 90D，拍照时要将相机放在样本的中心位置，每组拍摄2张照片，避免个别误差对植被覆盖度的提取造成影响，保证所有照片中植被覆盖度都代表了实际的植被覆盖度，在MATLAB R2016a软件中利用照片中植物枝叶的像元数与照片中总像元数之比进行计算，再根据阈值法提取出植被覆盖度(vegetation coverage，VC)。植被覆盖度计算公式[7]如下。

(1)

式中，VC为植被覆盖度；Nveg为提取出植被枝叶的像元数；Nsum为整幅图像的像元数。

在整个试验期间各处理对黄瓜未见药害现象，黄瓜生长正常，对黄瓜安全，黄瓜叶色青绿，黄瓜果实鲜靓，对产量无不良影响。

1.4 植被指数选取

目前，利用植被指数与光谱数据进行相关性分析以及反演植被各种生理化参数是常用方法。本研究选取350～2 500 nm波段范围内原始光谱反射率中任意2个波段组合的差值指数(difference index，DI)、归一化指数(normalized index，NI)、比值指数(ratio index,RI)、重新归一化差异指数(re-normalize difference index，RDI)和修正简单比率(modified simple ratio，MSR)。计算公式[8]如下。

DI(Rλ1,Rλ2)=Rλ1-Rλ2

(2)

NI(Rλ1,Rλ2)=|Rλ1-Rλ2|/Rλ1+Rλ2

(3)

RI=(Rλ1,Rλ2)=Rλ1/Rλ2

(4)

(5)

(6)

式中，Rλ1、Rλ2为任意两波段光谱反射率。

1.5 连续小波变换

小波变换包括离散型小波变换(discrete wavelet transform，DWT)和连续型小波变换(CWT)，由于离散型小波变换会随着分解尺度的增加而减少样本的光谱维数，不能对植被光谱进行有效的特征信息提取。因此，本研究选用CWT对植被光谱数据数据进行不同尺度的分解(Ψa,b)，生成在不同分解尺度与不同波长上的小波系数[Wf(a,b)]，由波长和分解尺度构成的二维矩阵，将一维高光谱反射数据经过连续小波变换转变成二维小波系数。小波系数可以提取出植被反射光谱吸收特征的形状，并提取出特征参数与敏感波段[9]；连续小波变换有许多小波基函数，经过对比与分析后，本研究选择Daubechies小波系中的db4母小波基函数，为了避免过多的分解尺度，选取1、2、3、4、5、6、7、8、9、10为小波系数的分解尺度，通过MATLAB R2016a对植被光谱数据进行连续小波变换。

(7)

式中，Ψa,b为连续小波分解，a为伸缩因子，b为平移因子，λ为植物高光谱数据的波段数。

(8)

式中，Wf(a,b)为不同分解尺度的小波系数；f(λ)为植被光谱反射率。

1.6 模型构建与精度验证

PLSR最开始来源于分析化学，现在已经在许多领域应用，属于多元统计回归方法之一，是相关分析、主成分分析、多元线性回归分析的集合体[10]。PLSR主要适用于含有多个自变量或多个因变量的回归分析，可以将高光谱数据降维，利用有效数据进行建模；PLSR还会在建模的同时考虑自变量和因变量中主成分的提取，建模精度更高。

SVM方法是基于统计学基础的一种新型机器学习方法，被用来解决分类和非线性回归等问题，通过多次训练使得模型最优化，选用RBF(radial basis function)为核函数，采用网络搜索优化思想对c和g值进行优化，从2-10到210进行优化，找出最优解c和g，并得出最小交叉验证均方误差(mean square erro，MSE)。此方法结构简单，可以较好地预测植被覆盖度。

本文将植被指数与小波系数作为自变量建立PLSR回归模型和SVM模型，将70组样本中的52组作为训练样本，18组作为验证样本；高光谱预测模型的准确性评估主要基于决定系数(R2)和总均方根差(root mean square error，RMSE)，即R2值越大，则建立模型的稳定性越好；RMSE值越小，建立模型的准确度越高，预测能力越强。

2 结果与分析

2.1 不同植被覆盖度光谱特征分析

单株蒺藜与蒺藜群落所表现出来的光谱曲线会随着植被覆盖度发生变化，图2为不同植被覆盖度(10%～50%)原始光谱反射率曲线。从整体来看，随着植被覆盖度的增加，光谱曲线的“五谷四峰”特征越来越明显。在可见光400～760 nm波段范围内，红边位置附近的“两谷一峰”特征逐渐突出，主要由于叶绿素含量也随植被覆盖度发生变化；在近红外760～1 300 nm波段范围内，主要受植被内部结构的影响，导致光谱反射率出现变化；在短波红外1 350～2 500 nm波段范围内，光谱反射率受植物中水分与CO2的影响，光谱曲线呈下降趋势。

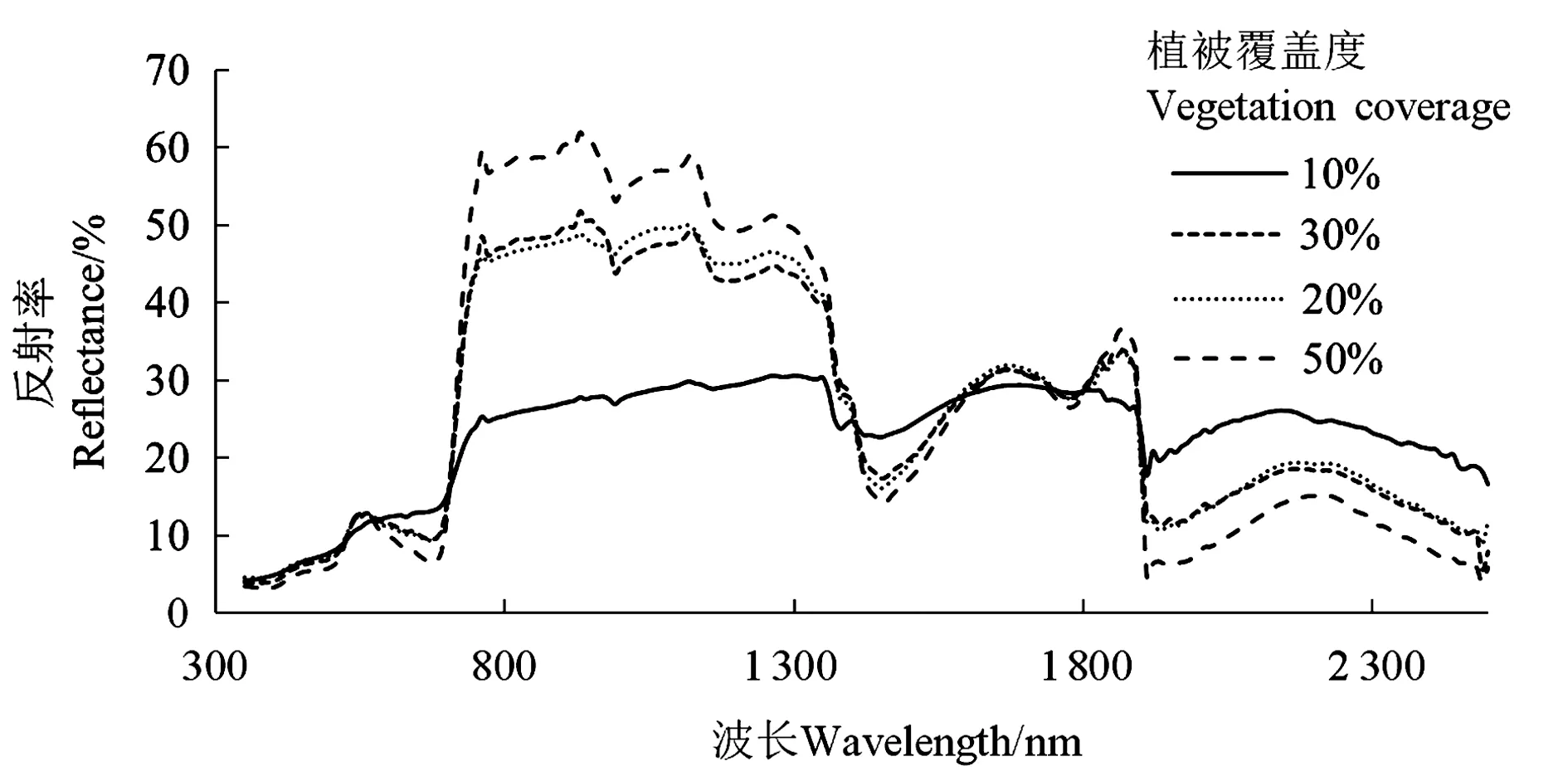
图2 不同植被覆盖度原始光谱反射率曲线Fig.2 Original spectral reflectance curves of different vegetation coverage

2.2 两波段原始光谱植被指数与植被覆盖度的相关性

图3显示,5种指数中，比值指数(RI)表现形式最好，其次是修正简单比率(MSR)、归一化指数(NI)、差值指数(DI)、重新归一化差异指数(RDI),其中DI形式中组合较好的波段是560～620 nm与560～1 200 nm的组合和630～1 250 nm与1 300～2 350 nm的组合；RI中组合较好的波段是570～600 nm与570～1 770 nm的组合和1 275～1 550 nm与1 370～1 770 nm的组合；NI中组合较好的波段是570～600 nm与570～1 780 nm的组合和620～1 750 nm与620～2 350 nm的组合；RDI中组合较好的波段是350～750 nm与700～1 300 nm的组合和710～1 800 nm与1 300～2 150 nm的组合；MSR中组合较好的波段是700～750 nm与700～1 900 nm的组合和1 500～1 850 nm与1 500～1 850 nm的组合。5种指数形式中，与植被覆盖度相关性最好的波段分别是DI(2 260 nm，2 210 nm)、RI(1 410 nm，660 nm)、NI(1 470 nm，670 nm)、RDI(1 770 nm，670 nm)、MSR(1 410 nm，660 nm)。图4为5种参数与植被覆盖度的相关性趋势图，5种参数中的最优波段与植被覆盖度相关性最好的植被参数为比值植被指数，相关系数为0.636 3，其次为归一化植被指数和修正简单比率指数，相关系数均达到0.6以上。

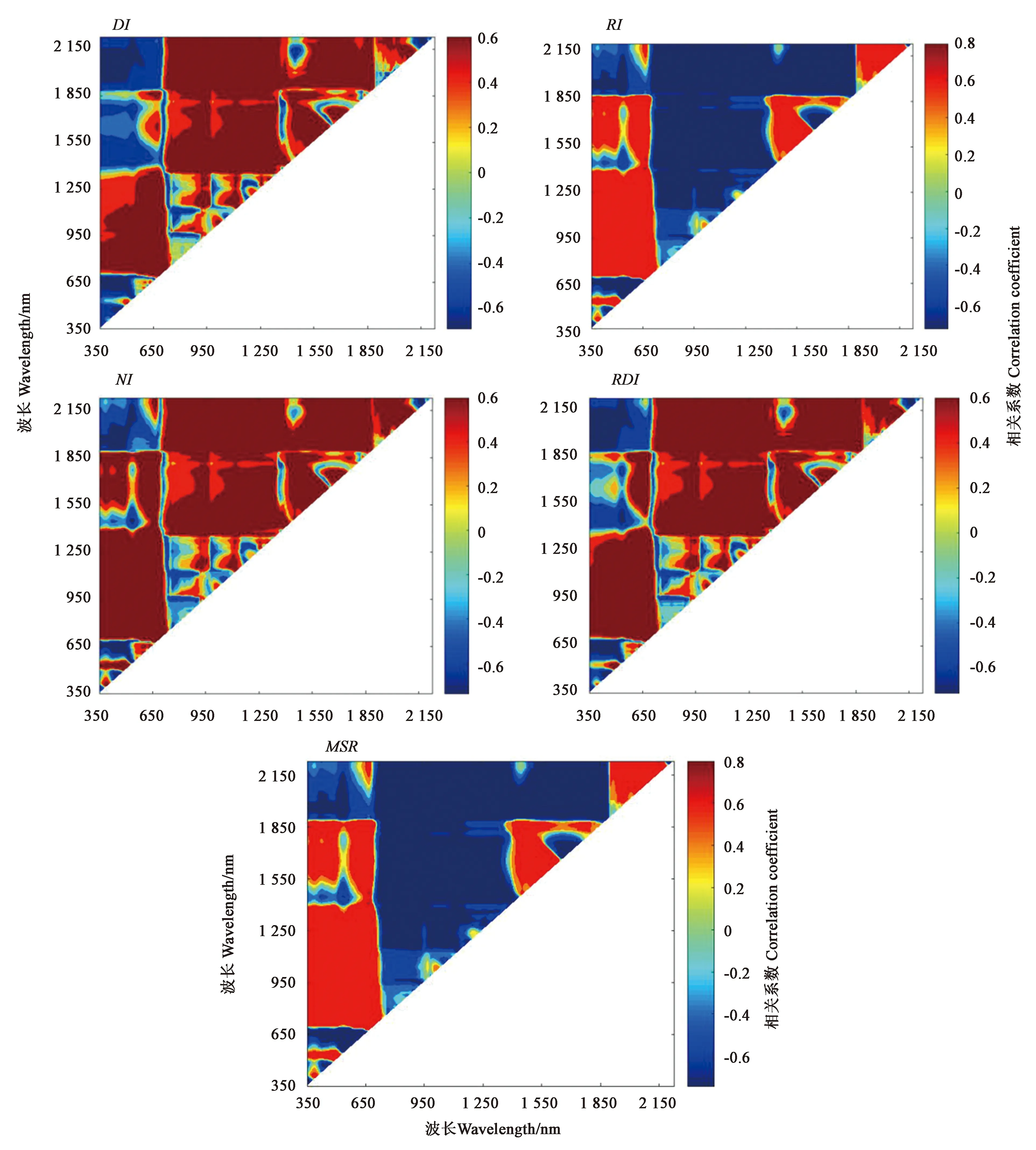
图3 两波段原始光谱指数与植被覆盖度的相关性Fig.3 Correlation between two-band original spectral index and vegetation coverage

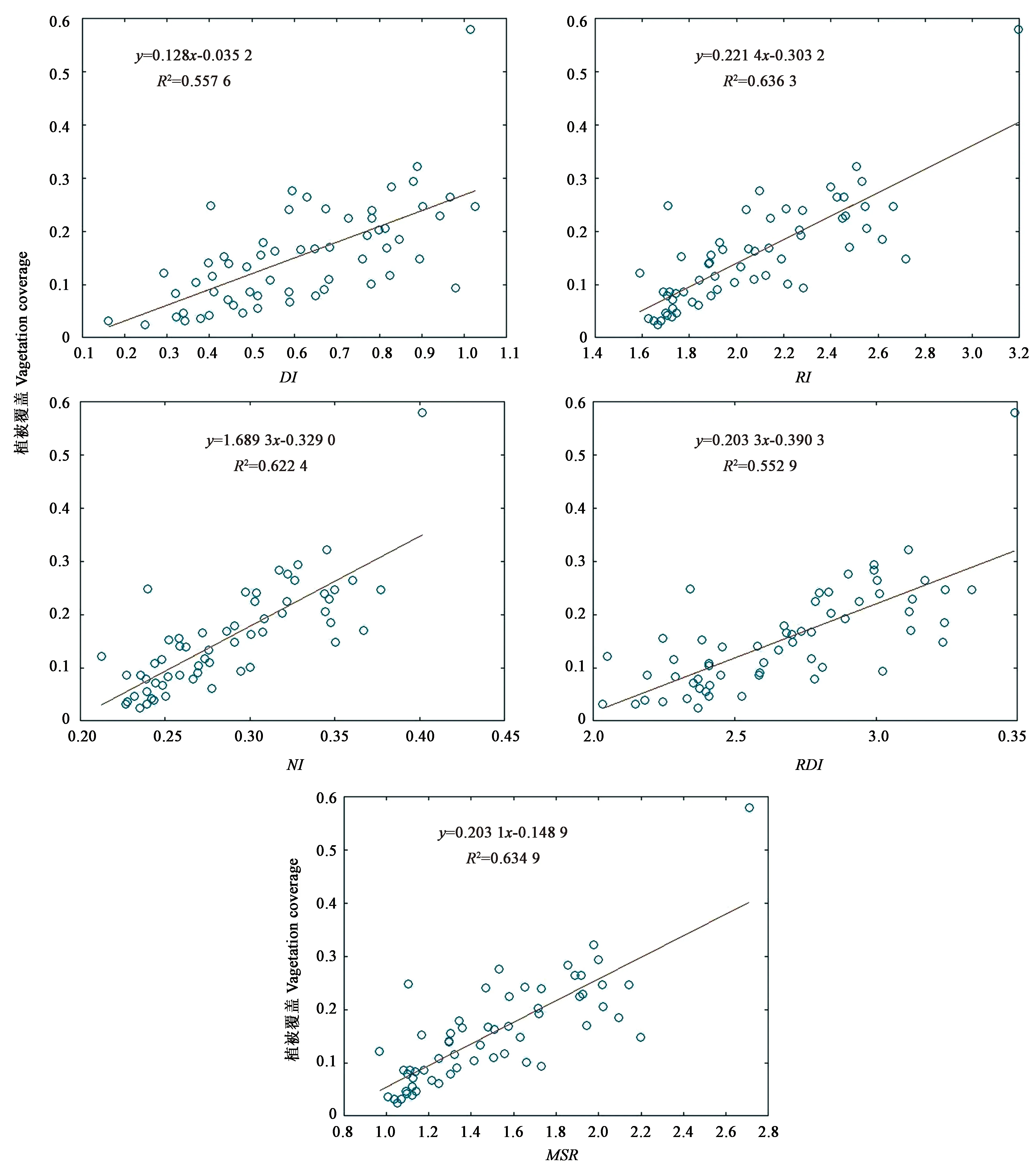
图4 最优波段与植被覆盖度的相关性Fig.4 Correlation between optimal band and vegetation coverage

2.3 植被覆盖度与不同分解尺度小波系数的相关性分析

2.3.1连续小波变换光谱曲线 蒺藜高光谱数据经过连续小波变换后光谱曲线变化情况见图5。不同分解尺度的光谱曲线表现的形态基本一致,具有明显的规律，但变化起伏较大；分解后不同尺度的小波系数将原始光谱中吸收峰与吸收谷的位置放大；与原始光谱曲线对比后可知，光谱曲线特征随着尺度的增加而增强，小波系数与光谱信号也逐渐增大；与原始光谱曲线特征位置进行比较后，可以看出：随着分解尺度的增加，在500、600、670、900、1 000、1 200、1 450、1 950 nm的波谷位置均发生“蓝移”的现象，向蓝波方向持续移动；在550、750、950、1 100、1 500、1 870、2 010 nm的波峰位置出现向右“红移”的现象，逐渐向红光波段移动。从结果来看，利用连续小波变换不但可以加强信号反射的强度，也可以将光谱特征参数放大，有利于对蒺藜光谱特征进行深入分析。

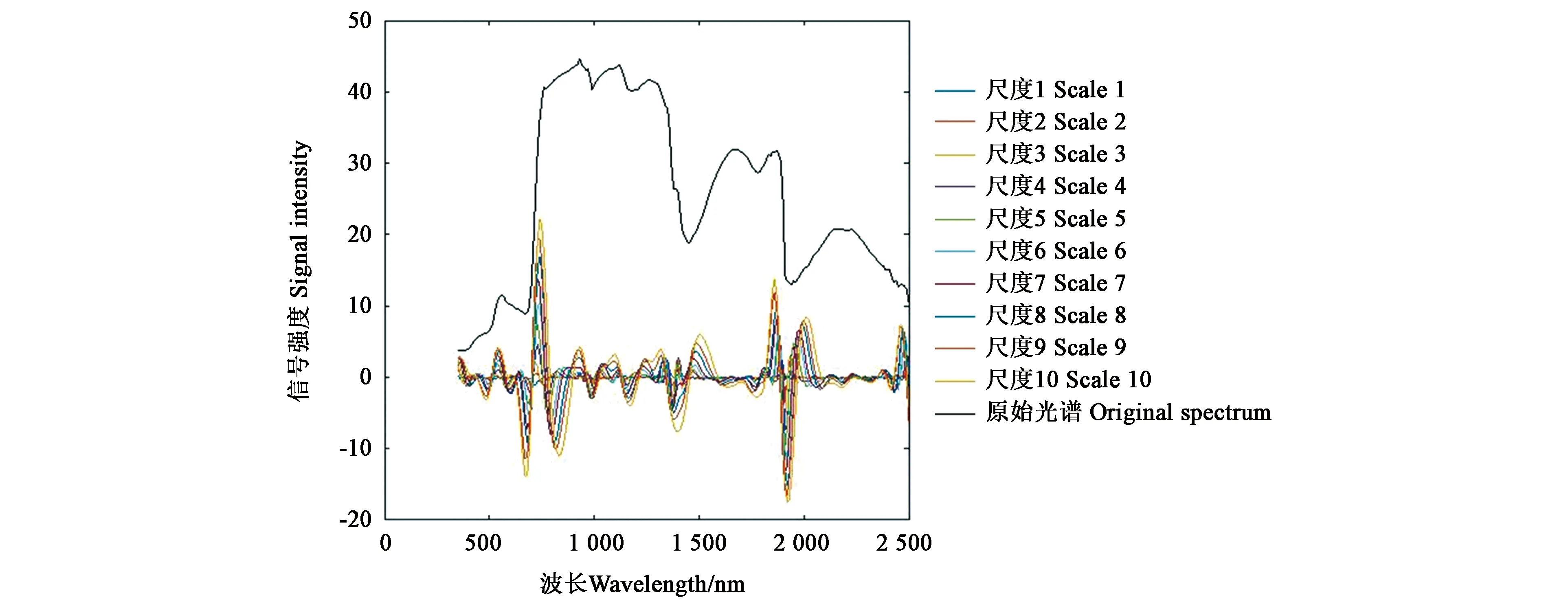
图5 1～10尺度分解光谱曲线对比Fig.5 Comparison of 1～10 scale decomposition spectral curves

2.3.2不同分解尺度小波系数与植被覆盖度的相关性 图6为不同分解尺度(原始光谱、一阶微分光谱、二阶微分光谱)小波系数与植被覆盖度的相关系数矩阵。图中红色的区域均代表相关性强的地方，颜色越深，代表相关性越大。原始光谱的植被覆盖度敏感波段主要集中在可见光波段(500～800 nm)、近红外波段(1 200～1 350 nm)和短波红外波段(1 800～2 050 nm、2 200～2 300 nm)。每个分解尺度对应的相关系数分别为0.720 1、0.735 7、0.741 6、0.724 8、0.763 9、0.788 9、0.769 1、0.780 7、0.761 4、0.760 1，其中尺度6相关系数最高，对应的波段为630 nm。一阶微分的植被覆盖度敏感波段主要集中在可见光波段(450～950 nm)、近红外波段(1 200～1 300 nm)和短波红外波段(2 200～2 350 nm)。每个分解尺度对应的相关系数分别为0.728 5、0.738 0、0.709 2、0.707 0、0.768 5、0.806 9、0.762 3、0.770 3、0.735 2、0.774 5，尺度6的相关系数最高，对应的波段是590 nm。二阶微分的植被覆盖度敏感波段主要集中在可见光波段(350～859 nm)和短波红外波段(1 800～2 100 nm)。每个分解尺度对应的相关系数分别为0.691 1、0.632 6、0.615 1、0.642 6、0.763 8、0.781 8、0.744 0、0.765 9、0.730 3、0.756 3，尺度6的相关系数最高，对应的波段是510 nm。

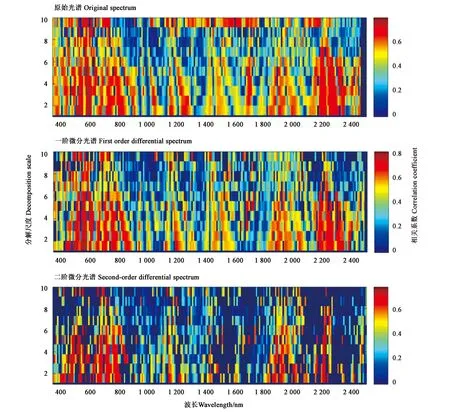
图6 不同分解尺度小波系数与植被覆盖度相关系数矩阵Fig.6 Correlation coefficient matrix of wavelet coefficients and vegetation coverage at different decomposition scales

2.4 植被覆盖度高光谱反演模型的优选

以原始光谱反射率提取的植被指数以及经过CWT提取的10组最优小波系数为自变量，建立与植被覆盖度PLSR回归模型、SVM回归模型。为了获得最佳的支持向量机模型，通过支持向量机函数的训练，得到最优的c与RBF核函数中的g参数，图7为支持向量机中最优c、g选择图。植被指数最优c=4，g=0.125；原始光谱小波系数最优c=102 4，g=0.003 9；一阶微分光谱小波系数最优c=32，g=8；二阶微分光谱小波系数最优c=102 4，g=32。由表1可以看出,植被指数、小波系数植被覆盖度都有一定的相关性，经过CWT后所建立的模型比原始光谱反射率建立的模型精度高，更具有可行性。以植被指数为自变量建立的模型中，SVM回归模型的相关系数最高，模型精度达到0.859 9；以不同导数变换后提取的小波系数为输入量建立的模型中，SVM模型的相关系数与检验精度没有PLSR模型效果显著，模型不稳定。经过以上对比与分析，以二阶微分小波系数为自变量的PLSR模型精度最高，可以很好地实现植被覆盖度的估算，而且方法简单，便于操作。经过CWT处理后的光谱数据不仅可以放大植被的特征信息，也可以提高建模时的精度，使模型更加稳定，有利于植被覆盖度以及其他生理化参数的估算研究。

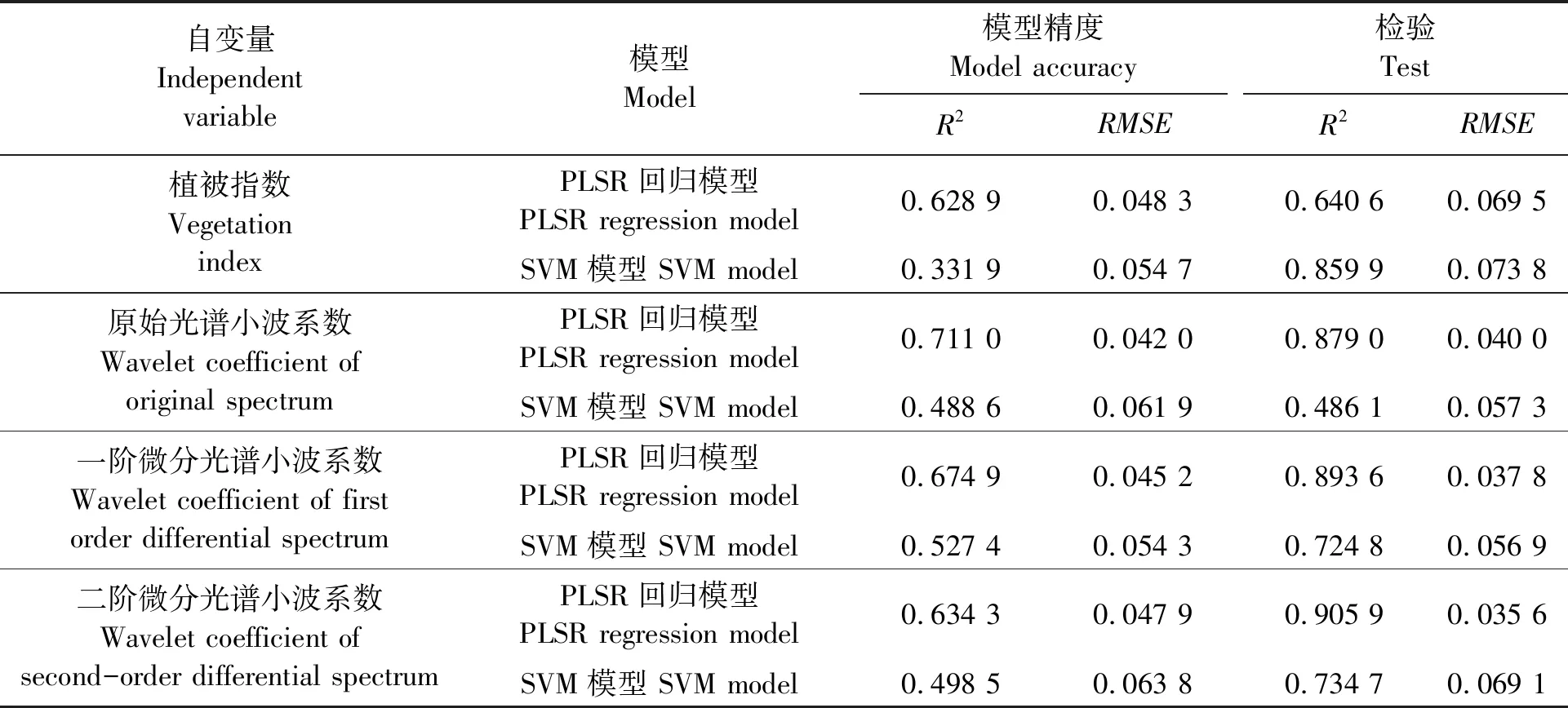
表1 植被覆盖度估测模型的建模集与预测集结果Table 1 Vegetation coverage estimation model modeling and prediction set results

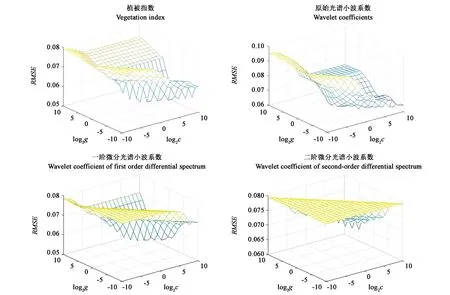
图7 SVM最优c、g选择Fig.7 SVM optimal c,g selection

3 讨论

不同植被类型光谱反射率曲线由于生长环境、内部因素等差异表现出的光谱曲线并不完全相同，但是表现形式都为“五谷四峰”形式。因此，本研究不只是针对蒺藜，其他植被均适用。对植被原始光谱反射率进行植被指数提取、导数变换并提取小波系数，有助于凸显出植被光谱特征，利于不同植被覆盖度含量的光谱曲线特征变化分析。这与李栋[11]的研究结果一致，构建连续小波变换反演模型代替原始反射率构建的反演模型，反演结果更为突出，显著地提高了模型的精度。经过对比与分析可知：以不同导数变换小波系数为自变量比植被指数为自变量的建模精度最高；2种建模方法中，二阶微分变换的小波系数与PLSR结合后的现象最好，可以有效地解决噪声以及外界因素等影响，将植被覆盖度很好地估算出来。国内外学者利用CWT对固沙植被的研究相对较少，研究主要集中在土壤有机质、农作物等方面，因此本研究采用CWT对蒺藜进行光谱处理具有新意。

本文所优选的植被指数都是较常见的，但是该方法有一定的局限性，不具有普适性，随着操作方式和测量条件的变化，优选植被指数的波长也会发生变化，但是经过CWT可以使整个光谱波段有序地分解，提取出的小波系数建立的模型适用性较强。刘小军等[12]与Maire等[13]均选取了几种典型植被指数，通过任意波段组合建立植被指数空间，在监测水稻等植物均有较高的监测精度。利用CWT处理光谱信息不但可以突出植被光谱特征，也可以将光谱隐藏信息挖掘出来，更有利于植被覆盖度的预测，具有十分重要的意义，这与Cheng等[14]的研究结果一致；由于具有较多的连续小波基函数，在今后研究中将进一步深入分析不同小波基函数对植被光谱的变化情况。

本研究结果表明，原始光谱植被指数与植被覆盖度呈显著相关；利用CWT变换不仅可以增强光谱的特征信号，提取出的小波系数也与植被覆盖度之间有良好的相关性，3种光谱变换后的小波系数与植被覆盖度均具有良好的相关性，经过一阶微分变换后小波系数与植被覆盖度相关性最大，具有良好的效果；以原始光谱植被指数和(原始光谱、一阶微分光谱、二阶微分光谱)CWT提取出的小波系数为自变量建立的4种模型中，经过CWT处理后的光谱数据建立的模型精度最高；利用CWT可以提高植被光谱中的有效特征信息，PLSR可以作为反演植被中其他生理化参数的方法，为植被监测提供更有效的参考价值。