基于正交试验的制粒机成型仿真及结构参数优化
杨涛涛,周星宇,陆晓丽,钱善华,俞经虎
(江南大学机械工程学院,江苏省食品先进制造装备技术重点实验室,江苏 无锡 214122)
环模制粒机由于制粒过程稳定、生产效率高、能耗低、成型率高等一系列优点[1]成为饲料生产的主要机械之一。近年来,国内外学者在环模制粒成型的功耗、颗粒成型质量和机理、力学特性、模辊磨损以及振动特性等方面进行了大量的研究,为环模制粒机的结构优化和工艺参数最佳匹配提供了宝贵的参考。Rolfe等[2]研究颗粒尺寸大小、环模转速和物料含水率三者对环模成型机物料成型的影响,结果表明,增大物料含水率、提高环模转速、降低物料尺寸可以提高物料成型压力和密度,但在成型过程也会增加产品温度。沈江飞[3]建立制粒机参数化多体力学模型,并设计正交试验分析多个因素对机器振动的影响规律,结果表明,增大主轴直径和支撑架刚度或减小压辊底座与主轴的连接刚度可有效降低转轴振动和挤压力变化幅值,而转轴轴承间距存在与轴承刚度相关的最优值。Kaliyan等[4]针对秸秆物料的压缩特性和致密过程物料的本构模型两方面进行研究,建立了其弹塑性固体模型,通过对物料的压缩试验,分析得出弹性模量和粘性系数与原料的耐磨性和抗压强度有关。王咏梅等[5]应用POLYFLOW软件对环模制粒机挤压区流场进行模拟,研究不同工艺参数对流场压力、速度、剪切速率和黏度分布特性的影响规律,发现喂料量为6 t·h-1、环模线速度为6.5 m·s-1和物料含水率为15%时所形成的流场有助于苜蓿草粉的制粒成型。李震等[6]采取流固耦合法对模辊关键部位进行疲劳寿命分析,结果显示,环模在靠近模孔位置处最容易发生疲劳破坏,其最小寿命为3.12×106次,并通过传统应力分析办法验证耦合法的可行性及有效性。制粒机结构参数的改变定然导致内部物料流动的变化,从而影响制粒机的成型效果。但是,由于物料的挤压过程复杂,目前较少通过模拟制粒机成型数值来研究结构参数对制粒效果的影响。因此,本文以谷物饲料为对象,应用COMSOL软件模拟分析物料在制粒机内挤压成型的流动过程,并基于正交试验,研究制粒机的结构参数对成型速率及能耗的影响,结合权矩阵综合分析方法提出最佳的结构参数组合。
1 原理与方法
1.1 环模制粒机成型原理
环模制粒机主要由喂料机、搅拌室和制粒机三部分组成。机器工作时,物料先是通过喂料机输送到搅拌室内,与室内喷嘴洒出的调质原料进行混合搅拌,提高含水率、黏度等特性。当完全搅拌后,物料便被送入制粒机,其内部运作截面如图1所示。根据所受压力不同,可将制粒机内物料运动区域分为三个区:送料区、变形压紧区、挤压成型区。
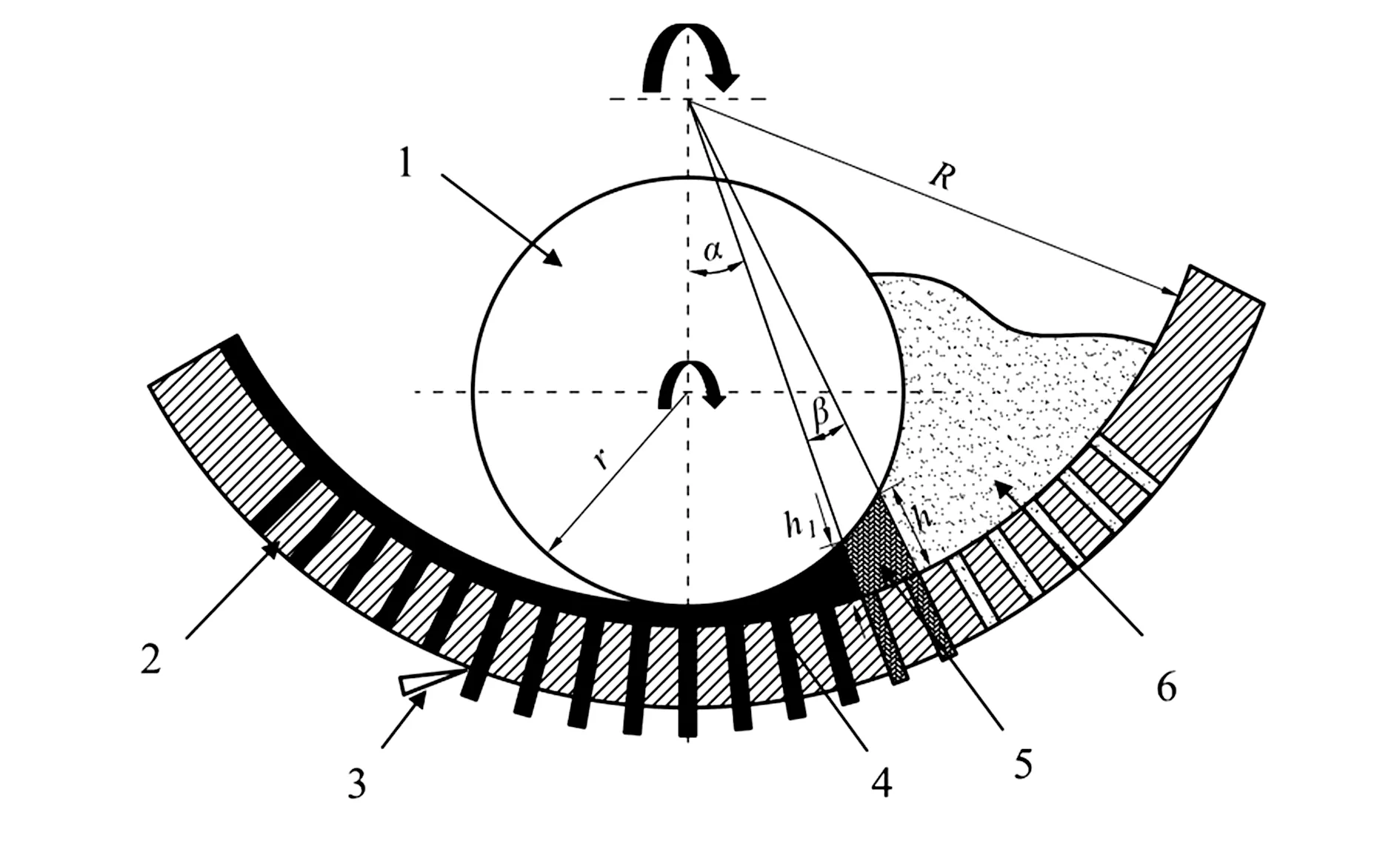
注:1—压辊;2—环模;3—切刀;4—挤压成型区;5—变形压紧区;6—送料区。Note:1—Pressure roller;2—Ring die;3—Cutter;4—Extrusion zone;5—Deformation compression zone;6—Feeding area.图1 制粒机结构Fig.1 Pellet mill structure
图中,R为环模内半径,r为压辊半径,x为模辊间隙,α为挤压成型区角度,β为变形压紧区角度,根据图1所示的几何关系推导α、β数值。
(1)
(2)
成型过程中,环模以一定角速度顺时针转动。物料首先进入到送料区,在环模的带动下,慢慢地向变形压紧区运动。在此期间,环模与压辊的间距变小,物料不断地受到挤压,密度增大,与辊面产生的摩擦推动压辊同样作顺时针转动,但转速比环模小。当运动到变形压紧区,物料继续受压挤,所受压强随弧长呈二次曲线增长[7](图2),少量物料也被挤出模孔。物料在挤压成型区所受压强基本为恒定值。在此区间,与压辊接触面的减少使得挤压力急剧增大,同时颗粒间的接触面积增大,物料产生较好地黏结,密度便稳定不变。当挤压力能够克服模孔内物料与孔壁摩擦时,物料便被挤出模孔,再通过切刀的切割,最终形成饲料颗粒。
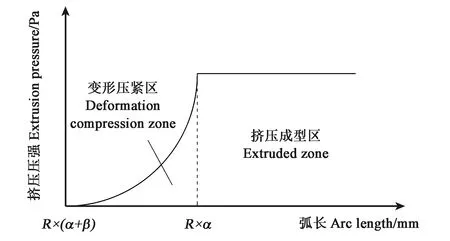
图2 物料所受压强变化趋势Fig.2 Change trend of pressure on materials
1.2 数值仿真
1.2.1数学模型 为了简化仿真计算,对数学模型作出以下假设:①物料运动为无弹性非牛顿流体流动,且考虑压缩性;②制粒机内各截面物料分布均匀;③忽略黏性生热及质量力的影响。本文依据SZLH420制粒机主要技术参数(表1)在COMSOL中建立了制粒机中心截面的流域模型(图3),流域由环模的旋转域和内部的固定流域组成,中间空白圆形区域是压辊所在位置。

表1 SZLH420制粒机主要技术参数Table 1 Main technical parameter of SZLH420 pellet mill

图3 制粒机中心截面流域Fig.3 Mathematical model of central section of pellet mill
1.2.2仿真参数及边界条件 流体流动的控制方程主要包括质量守恒方程、动量守恒方程和描述流体黏性的流变学本构方程[8]。在挤压过程中,物料以塑性存在于流域中;当剪切应力超过临界应力时,则表现为流体的流动特性。因此,本文采用HBP (Herschel-Bulkley-Papanastasiou)模型[9]对物料流变特性进行表征,其模型及等效黏度系数表达式如下。
ταβ=τβα=μB(εαβ)n+τy(1-e-mγ)
(3)
(4)
式中,μB为流动一致性系数,单位Pa·s;τy是临界屈服应力,单位N·m-2;m是模型参数,单位s,参数值越大,塑性存在时间越短;n是流动特性指数,n<1为假塑性流体,n=1为牛顿流体,n>1为膨胀性流体。
考虑到制粒前的调质搅拌过程,依据谷物饲料的初始属性(表2)设置仿真中进入制粒机前物料密度为845 kg·m-3,粘度流动一致性系数μB为650 Pa·s,临界屈服应力τy圆整为6 N·m-2。在环模内做挤压流动的物料可近似认为是假塑性非牛顿流体且处于塑性时间较短,因此流动特性指数n可设为0.95,模型参数m设为100。
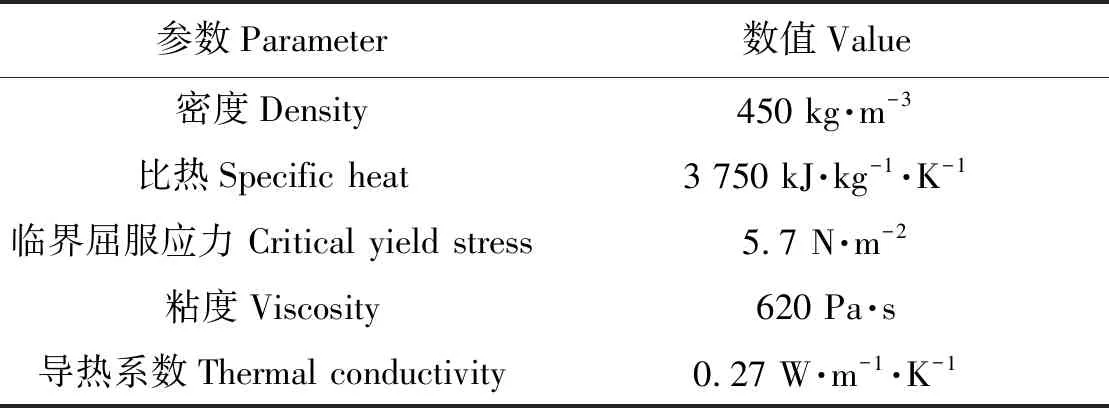
表2 谷物饲料参数Table 2 Grain feed parameter
入口边界设为质量流,流率0.4 kg·s-1,出口边界设为压力出口,压力为大气压,压辊处圆形壁面设为动网格,其余为无滑移壁面,摩擦系数为0.31。设置环模旋转域转速20 rad·s-1,并通过一致边界实现旋转域与固定域物料流动的连续性。
1.3 正交试验
1.3.1正交试验设计 制粒机的结构变化必然会造成成型速率及模辊能耗的变化。其中制粒机的环模内径、模孔长度、压辊直径以及模辊间隙是影响成型效果及功耗的主要参数,依据SZLH420制粒机的原始参数设计了一组L9(43)正交试验,参数水平如表3所示。并运用COMSOL软件对各个试验方案进行模拟仿真分析。

表3 正交试验参数Table 3 Pramater for orthogonal test
1.3.2试验指标 成型速率和能耗是评价制粒机工作的重要指标。通过仿真并不能直接反应这两个重要指标,需要进行数据转换。本文将单位时间内挤压成型区及变形压紧区的模孔平均产量Q(g·s-1)作为速率评价指标,其表达式如下。
(5)
式中,vi为单个模孔末端径向速率,单位 m·s-1;rm为模孔半径,为4×10-3m;n为区域模孔个数;ρ为物料密度,为845 kg·m-3。
能耗(W)指标主要由两部分组成[10],一是压辊碾轧功耗(W1),二是变形区、压紧区内物料受压挤出模孔的平均做功(W2),其表达式如下。
(6)
式中,P模辊间平均压强,单位Pa,可从仿真中获取;f为摩擦系数,为0.31;R为环模内径,单位m;B为模辊实际工作厚度,取0.1 m;α为挤压成型区角度,单位rad;β为变形压紧区角度,单位rad;Pi为单个模孔最大压强,单位Pa。
2 结果与分析
2.1 中心截面流域网格
依据物理场以及所设定的边界条件对制粒机中心截面流域进行较细化网格划分,局部效果如图4所示。模型边界处采用自由四边形划分,其余区域则是自由三角形划分,网格质量良好,并没有出现较大网格,可进行下一步仿真分析。

图4 局部网格划分Fig.4 Local meshing
2.2 仿真结果分析
从图5可以看出,速度场和温度场分布基本呈中心对称。模孔内物料由于环模顺时针转动具有较高的绝对速度,且离中心越远处速度越大,瞬时速度最高可达5.4 m·s-1。近环模及压辊壁面物料在摩擦力的作用下产生较快的流动。而模辊间物料运动速度普遍较慢,随着模辊间隙的减小,速度慢慢降低,甚至出现回流及涡旋的现象。这是因为该区域流动速度相对较低,无法克服沿流动方向正压强梯度的影响而造成的。

图5 仿真结果Fig.5 Simulation result
在压力场中,主要分为正压区及负压区。随着模辊间距减小,两区域物料逐渐被压缩,产生的反作用力愈来愈大,在接近最小间隙处正压区达到79.1 MPa,负压区达到78 MPa。而最小间隙处由于正负压的抵消,压强相对较低。模孔内,物料只受壁面摩擦力作用不再受压挤,压强沿模孔减小。总体来说,仿真结果符合实际物料运动过程,能够明显反映不同区域的流动状态。
2.3 正交结果分析
基于正交试验的仿真结果如表4及图6所示。单以产量为优化目标时,最佳方案为A2B2C1D1,即环模内径420 mm、模孔长度54 mm、压辊直径178 mm、模辊间隙1.5 mm,且产量主次顺序为D(模辊间隙)>B(模孔长度)>C(压辊直径)>A(环模内径);若以能耗小为优化目标时,最佳方案为A3B1C3D3,即环模内径425 mm、模孔长度52 mm、压辊直径182 mm、模辊间隙2.5 mm,且产量主次顺序为D(模辊间隙)>B(模孔长度)>C(压辊直径)>A(环模内径)。
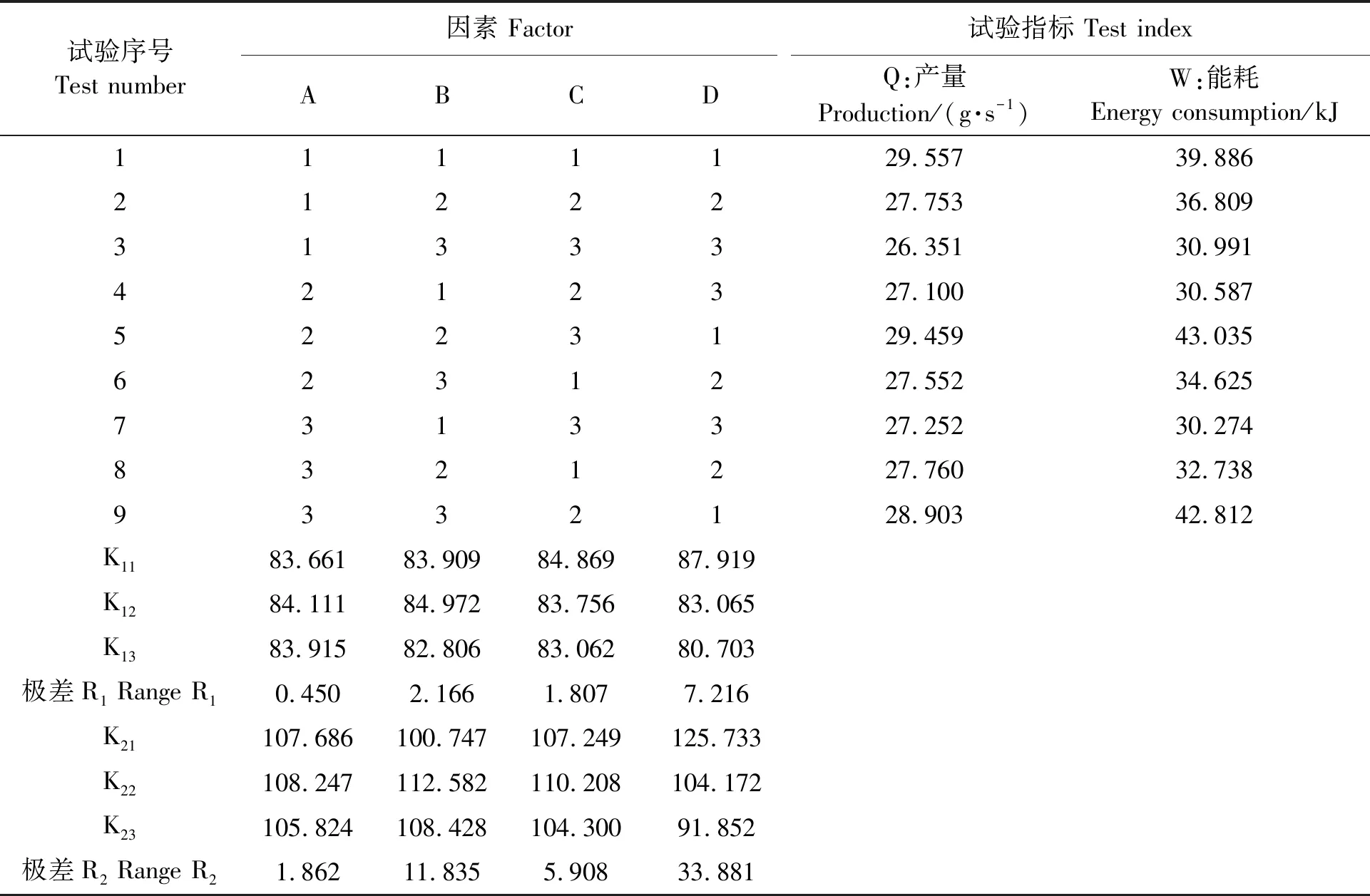
表4 正交试验结果Table 4 Result of orthogonal test

图6 各因素对指标影响Fig.6 Influence of various factors on indicators
2.4 权矩阵分析
2.4.1正交结果分析 从正交试验结果上看,产量高的方案明显能耗比较大。因此,为了获得产量高且能耗较少的综合方案,本文采用权矩阵方法优化选出最优方案。根据权矩阵原理[11],在计算产量的权矩阵时,指标以较大值为优化目标;在计算能耗的权矩阵时,指标以较小值为优化目标。最终计算出不同指标的权矩阵ω1、ω2,并由权矩阵平均计算可得到正交试验的综合评价的权矩阵ωa,其计算结果如下所示。
ω1=[0.012 9,0.012 9,0.012 9,0.062 0,0.062 8,0.061 2,0.052 4,0.051 7,0.051 2,0.216 6,0.204 6,0.198 8]T
(7)
ω2=[0.010 0,0.010 0,0.010 2,0.068 3,0.061 1,0.063 4,0.032 0,0.031 2,0.032 9,0.156 6,0.189 0,0.214 3]T×10-4
(8)
ωa=[0.006 5,0.006 5,0.006 5,0.031 0,0.031 4,0.030 6,0.026 2,0.025 9,0.025 6,0.108 3,0.102 3,0.099 4]T
(9)
从权矩阵中各因素水平的权重可知,因素A中A3的权重最大,因素B中B2的权重最大,因素C中C1的权重最大,因素D中D1的权重最大,因此以较高的产量、较低的能耗为优化目标的最佳参数为A3B2C1D1,即环模内径设置成425 mm,模孔长度设置成54 mm,压辊直径设置成178 mm,模辊间隙设置成1.5 mm。
2.4.2优化结果分析 再次运用COMSOL对优化后方案进行模拟,优化前后对比结果如表5及图7所示。对比各项指标得出,优化前后挤压区模孔末端平均速度v提高了0.022 m·s-1,产量指标增加了1.634 g·s-1,能耗指标增加了1.591 kJ。由图7可以看出,优化前后距中轴线小角度内(挤压变形区)的压力差距较大,最高可达约15 MPa;当角度大于15°时,两者的压力基本相同。总体来说,优化后的方案较之于优化前在环模的内表面压力增大,增大的压强使得模孔内物料挤出流动的速率加快,产量也相应提高,但同时能耗也加大。和其他正交试验方案相比,优化后的方案是在能耗增长不太大的情况下,制粒机的产量得到一定提升,从而使得整体制粒效率进一步提高。

图7 正压区环模内表面压力变化Fig.7 Pressure change of inner surface of ring die in positive pressure zone

表5 优化前后对比Table 5 Comparison result before and after optimization
3 讨论
目前,由于制粒机挤压过程的复杂性以及物料性质的特殊性,很少通过模拟制粒机内部流动过程来对其结构参数进行优化,大部分都是以挤压试验进行研究。丛宏斌等[12]依据成型机理建立压辊受力和物料成型能耗模型,绘制不同参数下压辊载荷分布曲线和能耗曲线,并以此提出设备的技术参数优化方法。但物料被压缩制粒过程很难通过挤压试验得出普遍性规律,这类方法相对于模拟流动仿真有一定的局限性且成本较高。因此,本文利用COMSOL仿真研究了制粒机环模内径、模孔长度、压辊直径和模辊间隙对成型性能的影响,发现通过对制粒机内部模型的仿真模拟,能够有效地反映物料在实际工作时的运动状态,对性能影响由大到小的结构因素排序为:模辊间隙、模孔长度、压辊直径、环模内径。采用权矩阵法确定优化后的最佳参数组合为环模内径425 mm、模孔长度54 mm、压辊直径178 mm、模辊间隙1.5 mm。相比于优化前,能耗虽然增大,但成型速率增加,能够有效地提高工作效率及性能。后期还可以改变COMSOL软件中材料参数、边界条件来研究不同物料和工艺参数对制粒机成型性能的影响,从而实现制粒机成型性能进一步优化。

