同轴套管式深井换热器的换热性能分析

付必伟，孙 琳，张 思

(长江大学 机械工程学院，湖北 荆州 434023)

引言

地热能作为一种可再生的清洁能源，具有资源量巨大、零排放污染、热能连续性好等特点[1-3]，可以有效替代煤炭等化石燃料，减少CO2排放对环境的影响，加快实现“碳达峰”和“碳中和”。开采地热能的方式主要有“取水取热”型和“取热不取水”型两种，其中“取热不取水”型采用循环流体换热，避免了直接“取水取热”导致的腐蚀结构以及回灌等问题，市场应用广泛[4]。井下换热器是“取热不取水”方法的关键技术，目前，常见的井下换热器形状包括：单/双 U 形、螺旋形及同轴套管等。其中，同轴套管式深井换热器(Coaxial Borehole Heat Exchanger，CBHE)因其换热面积最大，换热效率较高而被广泛应用[5]，但其换热性能的影响因素及变化规律还有待进一步研究。

近些年国内外许多学者采用解析方法和数值方法对同轴套管式深井换热器换热性能进行了分析，得到了许多有意义的结果。在解析方法方面，LUO Y Q等[6]通过建立一个分段的有限圆柱热源模型，研究了深井换热器的管道尺寸比、入口热流量和初始土壤温度分布函数对换热性能的影响； BEIER R A等[7]建立了同轴钻孔的瞬态传热模型，并基于拉普拉斯变换得到岩石层变化的解析解；孔彦龙等[8]介绍了OpenGeoSys数值模拟软件在浅层地热能的流体温度变化预测、水热型地热能开发过程中的采灌井距优化、结垢机理和干热岩开发过程中的渗透性演化等方面的应用实例；马玖辰等[9]基于建立深井换热器进(出)水管、固井水泥温度以及热储层过余温度的瞬态解析解，结果得到随着渗流速度的增大，深井换热效率会得到增强。在数值分析方面，卜宪标等[10-12]、冉运敏等[13]通过建立单井数值模型进行模拟研究，得到保温材料导热率越低，采出水温度以及取热功率越高；保温深度越深，进出口温差越大等结论；鲍玲玲等[14]通过数值模拟，研究了环腔流体流速、管径比、内管导热系数、岩土导热系数以及井孔深度对地埋管换热器传热性能的影响；黄文博等[15]通过数值模拟，对比分析了裂隙热储中的自然对流现象对重力热管地热系统与套管式地下换热器系统性能的影响；吴晅、刘俊等基于有限元分析方法，建立套管式地埋管三维非稳态传热模型，分析了回填材料、流体进出口方式、不同管径组合等工况下的套管式地埋管换热器传热特性[16-19]。NOOROLLAHI Y等[20]对废弃油井改造为地热井进行发电开展了研究，分析了循环流量对发电功率的影响。

综上所述，以往学者基本采用解析模型与数值计算的方法对深井换热器的传热性能进行研究，主要针对换热器的结构、运行方法以及地层的参数变化等。然而，在建立数学模型过程中通常忽略保温管插入深度对换热器采热功率的影响；同时，解析模型与数值计算不能描述换热器横截面传热过程，而数值仿真技术具有可视化的优势，可以更加具体的反映换热器结构参数对换热器采热功率的影响。为此，采用了数值仿真方法，基于有限体积法，通过建立套管式同轴换热器与温度梯度的耦合传热模型，分析了深井换热器的换热过程，计算出模型的温度场分布和速度场分布。研究了入口流速、入口温度、保温管距井底距离对换热性能的影响，为同轴套管式深井换热器的应用提供理论依据。

1 换热基本原理及评价指标

1.1 基本原理

同轴套管式深井换热器的工作原理如图1所示，换热器主要包括热岩石、注入通道、采出通道、保温管和井壁组成。井壁和保温管组成的环腔部分作为注入通道，保温管作为采出通道，注入通道底部封死，流体从注入通道流入，到达井底后由于压力反向从采出通道流出，注入流体通过与井壁和热岩石进行换热后，产生高温流体，经保温管流出。

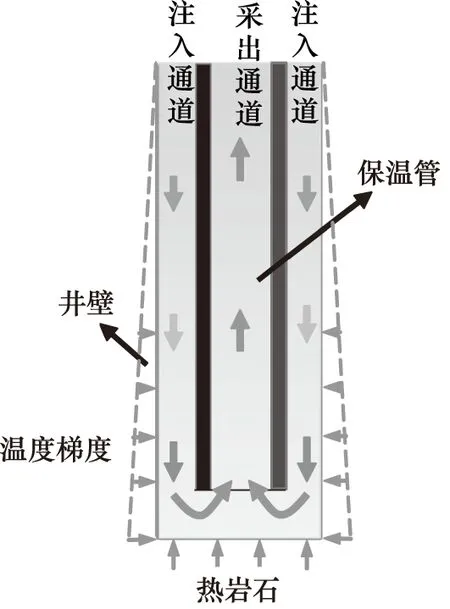
图1 同轴套管式深井换热器的工作原理图Fig.1 Working principle diagram of coaxial casing deep well heat exchanger

1.2 换热性能评价指标

换热器的换热性能主要采用采出温度和采热功率进行评价。其中，采热功率受流体的物性参数、流道尺寸、流体流速以及进出口温差等因素的影响，其表达式可表示为[20]：

Qout=cρρArvout(Tout-Tin)

(1)

式中，cρ—— 流体的比热容

ρ—— 流体的密度

Ar—— 保温管流道直径

vout—— 采出流体流速

Tout—— 采出流体温度

Tin—— 注入流体温度

2 数值模型

2.1 模型假设

由于换热器与岩石换热的复杂性，为了更好的分析换热器的换热性能，建立仿真模型过程中，作合理假设如下[21]：

(1) 将地热井下同轴套管换热器周围的岩土看作均匀介质，忽略地下水渗流作用的影响，把地下岩土中的传热视为纯导热；

(2) 数值模拟区域径向边界处的温度视为恒定；

(3) 井底热源和地表的温度视为恒定；

(4) 由于井筒长期贴合岩石，岩石与井壁的温度视为相同。

2.2 几何模型与网格离散化

建立同轴套管式换热器流道的三维模型以及网格划分，如图2所示。为了便于计算以及更加集中的研究换热器的换热效果，取换热器井底h1=10 m分析，同轴套管式换热器的外管直径为177.8 mm，保温管外径为120 mm，保温管厚度为10 mm，模拟中涉及的其他相关物性列于表1。

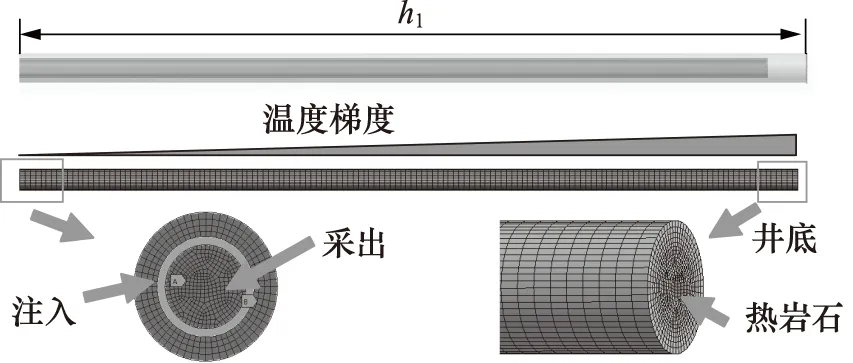
图2 几何模型及网格划分Fig.2 Geometric model and meshing

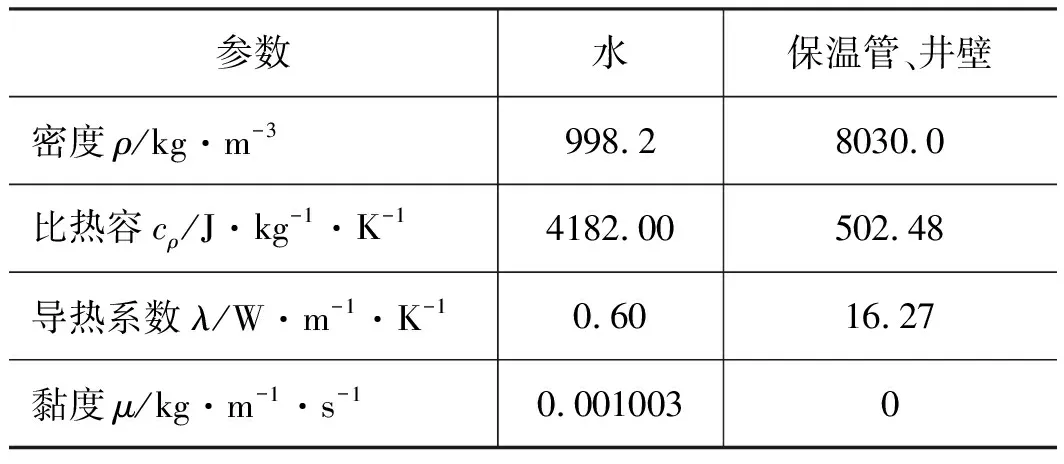
表1 物性参数Tab.1 Physical parameters

2.3 控制方程

通过对雷诺数计算，采用标准的k-ε湍流模型[22-23]，管内循环流体与管壁面之间的换热边界条件定义为耦合换热边界。

1) 连续性方程[24-25]

(2)

式中，ρ—— 密度

vi——i方向的流体速度分量

xi——i方向的微元段

Sm—— 相变源项

2) 动量守恒方程

(3)

(4)

式中，p—— 静压力

v—— 流体速度

vj——j方向的流体速度分量

xj——j方向的微元段

δij—— 克罗内克函数

τij—— 应力张量

pgi——i方向上的重力体积力

3) 能量守恒方程

(5)

式中，λ—— 流体的导热系数

Sh—— 相变时的能量源项

2.4 初始条件和边界条件

入口边界设为速度入口，出口边界设为压力出口。地表温度取恒温288.15 K，换热器底部边界设置为恒温408.15 K，井壁温度梯度采用UDF技术控制，取0.045 K/m。

1) 岩石的温度:

TW=Tsur+Tgz

(6)

式中，TW—— 岩石温度

Tsur—— 地表温度

z—— 井深

Tg—— 地温梯度

2) 出口的压力:

p出=ρ水gz

(7)

2.5 网格无关性

计算网格采取结构化网格，其中在保温管以及近壁区域进行了网格细化，为了保证计算结果不受网格划分数量的影响，需要进行网格无关性验证，为此设计了7种不同数量的网格计算方案。由表2可知，当网格数量大于474948时，采出温度基本保持一致，因此本研究中采用方案5中的网格方案进行计算。

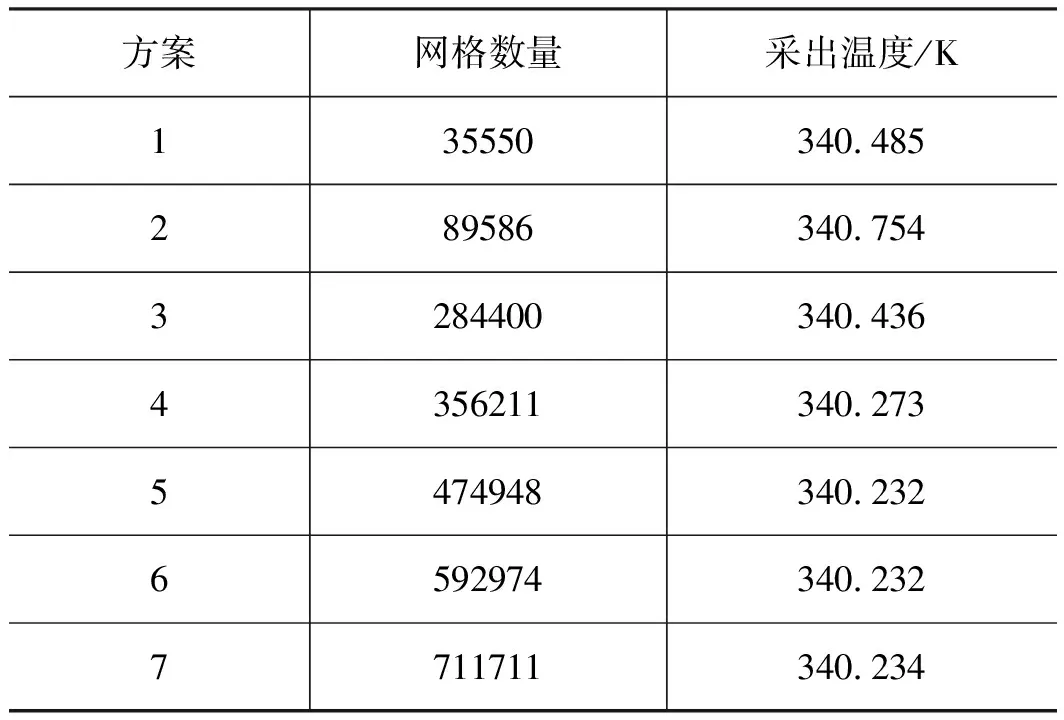
表2 网格无关性验证结果Tab.2 Grid independence verification results

3 结果分析

3.1 流场分析

1) 温度场分析

图3为换热器温度分布云图，从图中可以看到，低温流体由注入通道流入后，经过热岩石及井壁逐渐加热，到井底温度升至最高，通过保温管采出。数据提取线设置在管轴处以及注入通道中间；出口设置数据采集点，采集流道内温度及流速。

图3 换热器温度分布云图Fig.3 Temperature distribution nephogram of heat exchanger

2) 速度场与矢量分析

图4是换热器的速度分布云图，从图中可以看出，由于流体与壁面的黏滞力，流体在近壁面的速度都为0 m/s；同时结合图4中换热器井底流体的速度矢量可以明显看出，注入流体在井底与保温管的空隙处形成一个缓流区，流入保温管后由于流道减小，在保温管底部形成高速区，低速流体由于流速低，与岩石换热的时间更长，因此在换热器底部环空的流体温度较高，最后高温流体经由保温管流出。

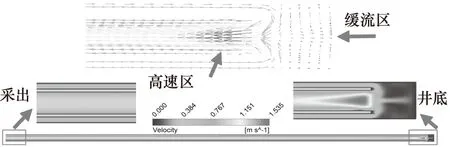
图4 换热器速度分布云图Fig.4 Velocity distribution nephogram of heat exchanger

3) 换热器的径向温度变化

图5为距井底不同距离，换热器截面上沿径向L1温度的变化曲线，从图5可以看出，在注入通道的流体与井壁的换热过程中，流体温度随着距井底距离的减小而逐渐增加。由于流体与井壁的对流换热效应，近壁面区流体温度较高，近壁面区域高温流体向注入通道中心低温流体传热，故沿着井壁到注入通道中心方向的流体温度逐渐降低；同理，靠近保温管区域的流体温度较高，从保温管区域到注入通道中心区域的流体温度逐渐降低，因此在注入通道的中心区域，由于同时远离井壁和保温管，其温度最低。

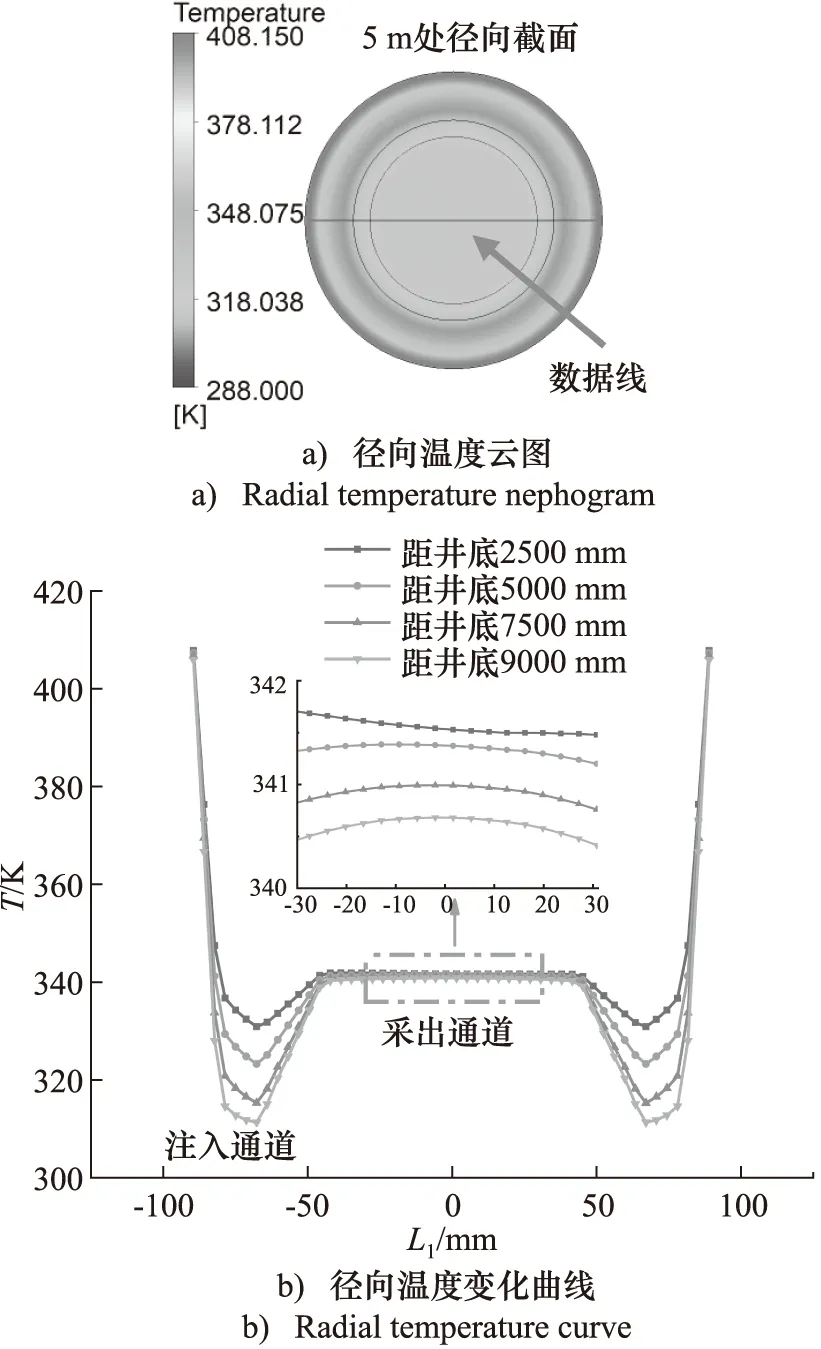
图5 换热器径向温度云图及径向温度变化曲线Fig.5 Radial temperature nephogram and radial temperature change curve of heat exchanger

如图5所示，随着与井底距离逐渐减小，注入通道内流体温度逐渐增加，由于保温管与注入通道流体换热，因此采出温度随着与井底距离的增加而逐渐降低。

3.2 入口流速对取热的影响

1) 入口流速vin对换热器内流体温度沿井深方向分布的影响

入口流速直接影响着换热器单位时间内的换热量。设定入口温度为310 K，出口压力为2.93 MPa，入口流速变化范围设计为0.1～1 m/s，其他参数见表1，不同入口流速下注入通道及采出通道内流体沿轴向L2的温度分布如图6所示。从图中可知，同一井深处，入口流速越低，注入和采出通道中流体温度越高，采出温度也越高，这是因为入口流速越低时，单位体积水与井壁换热时间越长，采出水温越高。

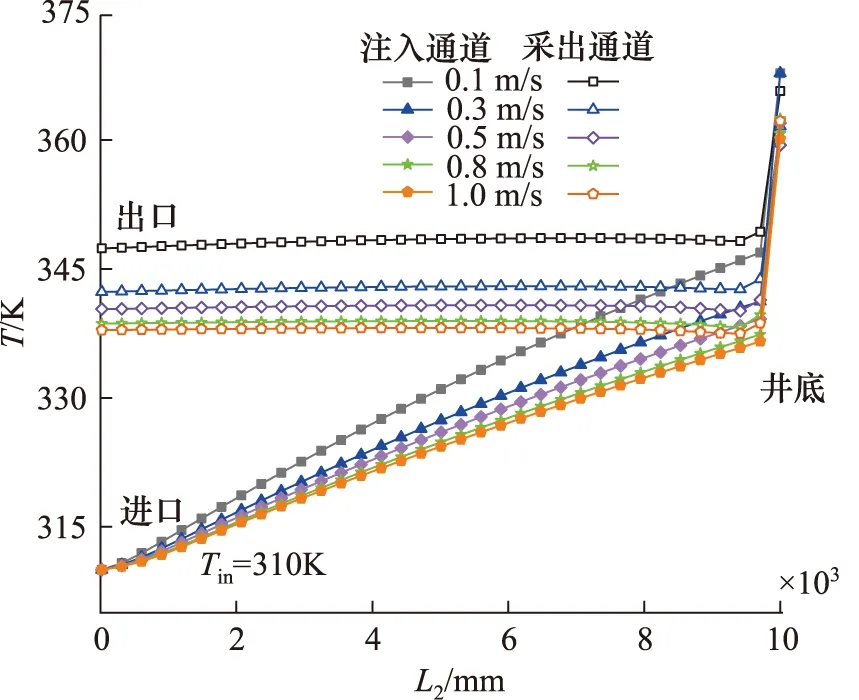
图6 注入、采出通道内流体沿轴向温度变化曲线Fig.6 Axial temperature change curve of fluid in inlet and outlet channels

图7为换热器沿轴向的速度与温度变化曲线，图中显示流体注入速度为0.5 m/s时，与壁面换热后流体温度逐渐上升，到井底流体温度升至最高，井底段温度上升较快。井底段流体流速较低，该处流体与高温岩石换热时间更长，因此井底段的温度变化最快且远高于注入通道和采出通道中的流体温度。

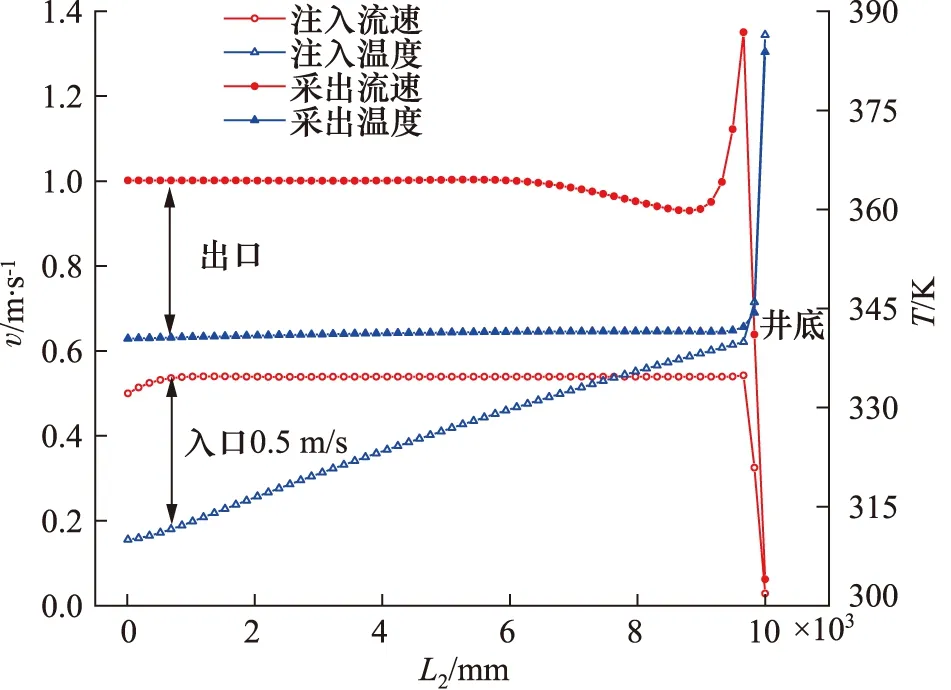
图7 换热器沿轴向的流速与温度变化对比图Fig.7 Comparison of speed and temperature changes along axial in heat exchanger

2) 入口流速对采出温度和采热功率的影响

图8为采出温度和采热功率随入口流速的变化曲线，图中显示入口流速越高，采出温度越低，采热功率越高。当入口流速从0.1 m/s增加到0.3 m/s时，采出温度下降了5.1 K；从0.3 m/s增加到0.5 m/s时，采出温度下降了2.34 K，这是因为入口流量增加导致单位时间内通过出口的流量变大且热短路现象减弱[21]。同时，当注入流体流速从0.1 m/s增大到1.0 m/s 的过程中，采热功率增大了7倍左右，但是采出温度降低了9.82 K。当流体的流速增大后，流体与壁面之间的对流换热效率增强，有利于提高采热功率，但是流体与壁面之间的换热时间减少，不利于采热功率的提高；同时流速增大，流体总量增大，不利于流体温度上升。因此在对流换热和换热时间的综合影响下导致流体温度降低，但是换热功率增大。

图8 采出温度和采热功率随入口流速的变化曲线Fig.8 Change curve of outlet temperature and heat recovery power with different inlet flow rate

增加流速增加采热功率，但是也导致增加了注入水泵的功率，对能量的输入有了更高要求[14]，因此，对于工程中选择注入水的流速可以选择综合考虑采热量、采出温度以及水泵的功耗。

3.3 入口温度对取热的影响

1) 入口温度对换热器内流体温度沿井深方向分布的影响

图9为入口速度0.5 m/s，不同入口温度下，流体在注入通道和采出通道内的温度分布曲线。图中显示在注入通道和采出通道内流体温度随入口温度增加而增大，同时流体沿注入通道和采出通道井深的变化规律保持一致。

图9 注入、采出通道内流体沿轴向的温度变化曲线Fig.9 Axial temperature change curve of fluid in inlet and outlet channels

2) 入口温度对采出温度和采热功率的影响

图10为采出温度与采热功率随注入流体温度的变化曲线，图中显示采出温度与流体入口温度呈线性递增的关系，而采热功率与入口温度呈线性递减的关系。由于入口温度增大，流体与热壁面的换热减少，导致换热器的采热功率降低。当流体流速为0.5 m/s，温度从288 K增加到308 K时，采出温度增加了4.31%，采热功率下降了17.20%。

图10 采出温度与采热功率随入口温度的变化曲线Fig.10 Change curve of outlet temperature and heat recovery power with different inlet temperature

3.4 保温管距井底距离对取热的影响

取入口流速0.5 m/s，入口温度310 K，其他参数见表1，模拟保温管与井底距离D为100～900 mm对于换热器取热的影响，见图11。由图可知，保温管与井底距离越长，井底聚集的缓流区越长，在保温管内形成的高速区域越大。结合图12不同插入深度保温管的轴向流速曲线可知，靠近井底的流体流动速度为0 m/s，与热岩壁换热时间更长，参与流动较少，与管内形成的高速区域不同，井底缓流区流体堆积，导致注入通道内流入流体还未与井底换热就流进保温管。

图11 保温管内流速分布云图Fig.11 Velocity distribution nephogram in insulation pipe

图12 保温管内轴向流速曲线Fig.12 Axial flow velocity curve in insulated pipe

1) 保温管与井底的距离对换热器内流体温度沿井深方向分布的影响

图13是保温管内流体温度沿轴向距离的变化曲线，图中可以看出，保温管与井底距离越小，采出温度越高。由于保温管与井底距离不同，造成井底缓流流体区域不同，导致注入通道流体还未与井底换热就流进保温管，因此保温管与井底距离越小(插入深度越深)，流体换热时间越长，采出温度越高。

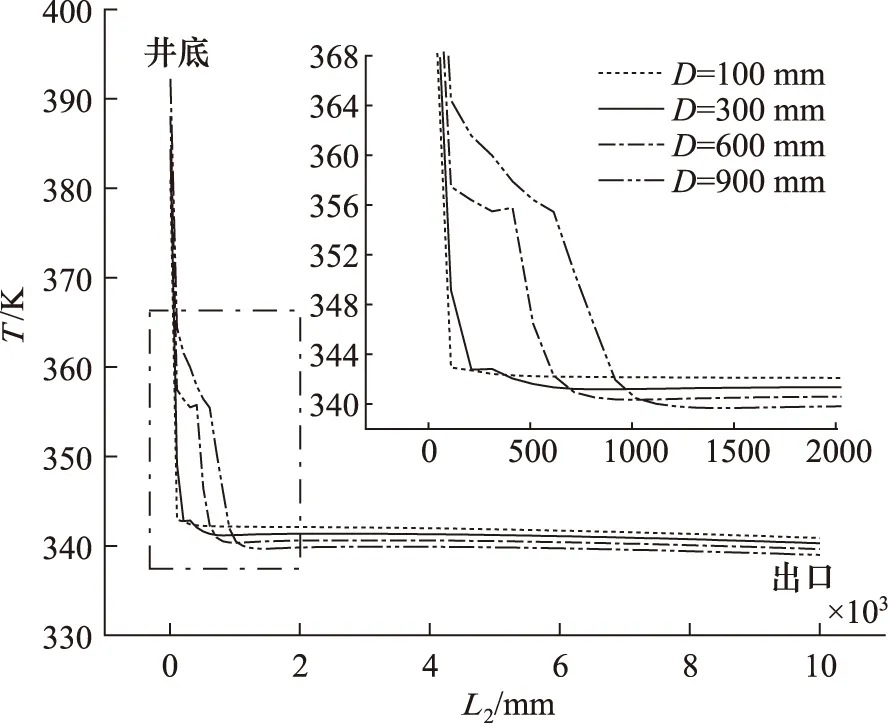
图13 保温管内流体温度沿轴向距离的变化曲线Fig.13 Axial temperature change curve in insulation pipe

2) 保温管与井底距离对采出温度和采热功率的影响

图14是保温管与井底距离和采出温度、采热功率的关系曲线，图中可以看出，保温管与井底距离和换热器流体采出温度、采热功率基本呈线性递减的关系，保温管与井底距离为100 mm时的采热功率为1012.25 kW，距井底900 mm时保温管的采热功率为949.86 kW，采热功率降低了6.16%。

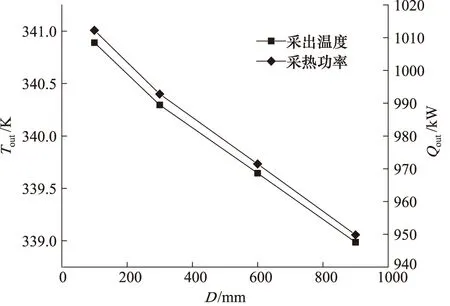
图14 采出温度和采热功率的变化曲线Fig.14 Change curve of outlet temperature and heat recovery power

4 结论

为了提高换热器的换热效率，建立了同轴套管式深井换热器的数值模型，采用有限体积分析方法分析了换热器的换热性能，得到如下结论：

(1) 采出温度随着入口流速的增加而降低，而采热功率大幅上升。入口流速由0.1 m/s增加到1 m/s，采出温度降低了9.82 K，采热功率增加了7倍；高流速对于水泵的功耗也有需求，因此工程中选择入口流体流速时可以选择综合考虑采热量、采出温度以及水泵的功耗；

(2) 增加注入流体的温度可以增加采出温度，但是采热功率会降低。入口温度从288 K增加到308 K时，采出温度增加了13.61 K，采热功率下降了17.2%；

(3) 降低保温管与井底的距离可以增加采热功率。保温管从距井底900 mm距离降低到100 mm，采出温度增加1.91 K，采热功率增加6.57%。